Expresiones Regulares Curso de Compiladores Preparado por Manuel



























- Slides: 43

Expresiones Regulares Curso de Compiladores Preparado por Manuel E. Bermúdez, Ph. D. Associate Professor University of Florida

Expresiones Regulares • Una descripción compacta y fácil de leer de un lenguaje regular. • Usamos operadores para denotar constructores de lenguajes, y construir lenguajes complejos a partir de lenguajes “atómicos” sencillos.

Expresiones Regulares Definición: Una expresión regular sobre un alfabeto Σ se define recursivamente: 1. 2. 3. 4. 5. 6. ø denota el lenguaje ø ε denota el lenguaje {ε} a denota el lenguaje {a}, para todo a Σ. (P + Q) denota L(P) U L(Q), donde P, Q son e. r. ’s. (PQ) denota L(P)·L(Q), donde P, Q son e. r. ’s. P* denota L(P)*, donde P is una e. r. Para evitar paréntesis excesivos, asumimos asociatividad izquierda, con la siguiente precedencia (de mayor prioridad a menor prioridad): *, ·, +

Expresiones Regulares Ejemplos: (O + 1)*: una hilera de O’s y 1’s. (O + 1)*1: una hilera de O’s y 1’s, que termina en 1. 1*O 1*: una hilera de 1’s con un O insertado. Letter (Letter + Digit)*: un identificador. Digit*: un entero. Quote Char* Quote: una hilera. † # Char* Eoln: un comentario. † {Char*}: otro comentario. † † Assumiendo que Char no contiene ‘Quote’, eoln, o ‘}’.

Expresiones Regulares Conversión de gramática lineal derecha a expresión regular Ejemplo: S → a. S → b. R →ε R → a. S ¿ Qué significa S → a. S ? L(S) {a}·L(S) S → b. R significa L(S) {b}·L(R) S → ε significa L(S) {ε}

Expresiones Regulares Juntas (las tres opciones de S) significan que L(S) = {a}·L(S) + {b}·L(R) + {ε} o bien, S = a. S + b. R + ε Similarmente, R → a. S significa que R = a. S. Entonces, S = a. S + b. R + ε R = a. S Sistema de ecuaciones simultáneas, en la cual las variables son los no-terminals.

Expresiones Regulares Solución del sistema de ecuaciones simultáneas. S = a. S + b. R + ε R = a. S Sustituimos R = a. S: S = a. S + ba. S + ε = (a + ba) S + ε Pregunta: ¿ Qué hacemos con ecuaciones de la forma X = X + β ?

Expresiones Regulares Respuesta: β L(x), así que αβ L(x), αααβ L(x), … y entonces, α*β = L(x). En nuestro caso, S = (a + ba) S + ε = (a + ba)*

Expresiones Regulares Algoritmo 5: Gramática Lineal Derecha → Expresión Regular 1. A = α 1 + α 2 + … + αn si A → α 1 → α 2. . . → αn

Expresiones Regulares 2. Si la ecuación es de la forma X = α, donde X no aparece in α, se reemplaza toda ocurrencia de X con α en todas las demás ecuaciones, y se elimina la ecuación X = α. Si la ecuación es de la forma X = αX + β, donde X no occurre en α o en β, se reemplaza la ecuación con X = α*β. Nota: Se puede necesitar manipulación algebraica para obtener la forma X = αX + β. Importante: La concatenación no es conmutativa!!

Expresiones Regulares Ejemplo: S→a → b. U → b. R R → aba. U →U U → a. S →b S = a + b. U + b. R R = aba. U + U = (aba + ε) U U = a. S + b Sustituimos R: S = a + b. U + b(aba + ε) U U = a. S + b

Expresiones Regulares Sustituimos U: S = a + b(a. S + b) + b(aba + ε)(a. S + b) = a + ba. S + bb + babaa. S + babab + ba. S + bb repetidas = (ba + babaa)S + (a + bb + babab) Y entonces, S = (ba + babaa)*(a + bb + babab)

Lenguajes Regulares Resumiendo: Listo RGR RGL Algoritmos 1, 2 Algoritmos 3, 4 Pronto DFA Mínimo Algoritmo 5 RE NFA DFA

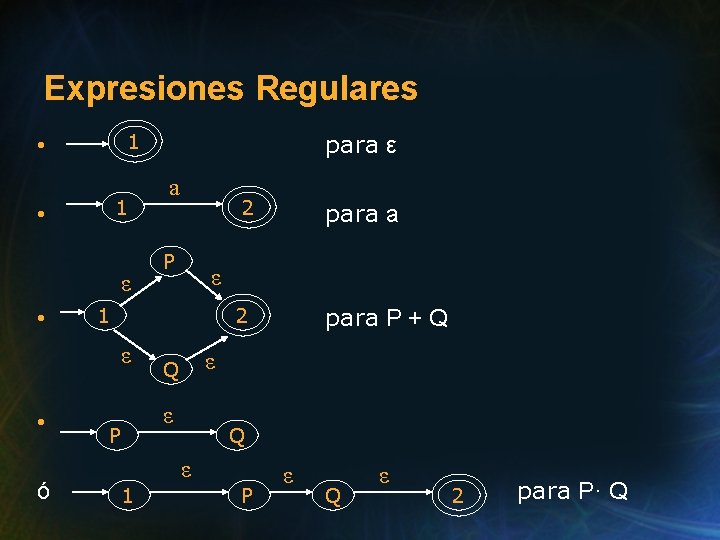
Expresiones Regulares Algoritmo 6 (Versión 1): Expresión Regular → FSA (Autómata Finito no-determinístico) Se construye el FSA recursivamente, según la estructura de la expresión regular. Cada FSA tiene un estado inicial, y uno final. Conversiones: 1 2 para ø

Expresiones Regulares 1 • ε • ó a P P 2 para a 2 para P + Q ε 1 ε • para ε 1 • ε Q ε 1 P ε Q ε 2 para P· Q

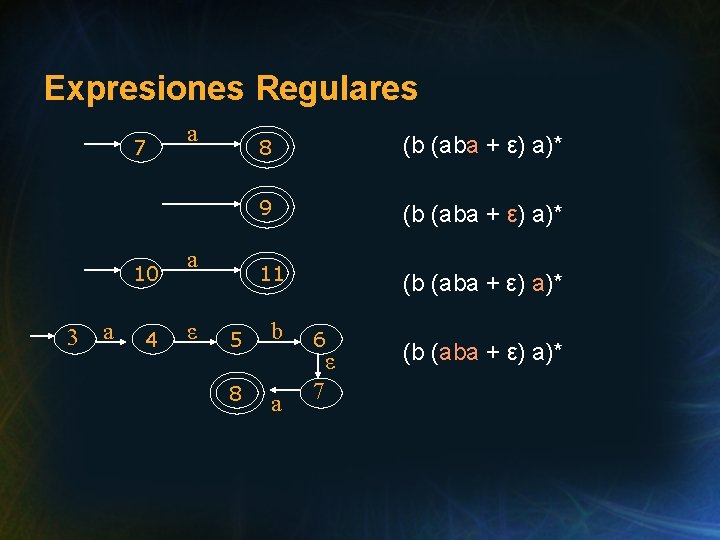
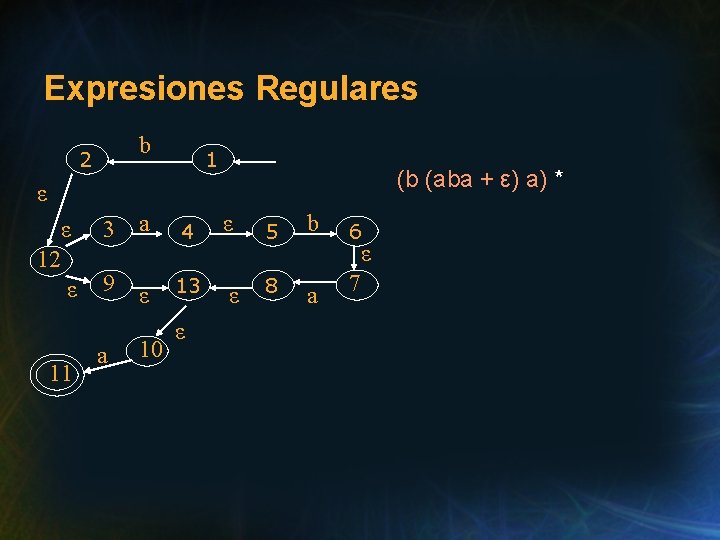
Expresiones Regulares 1 ε ε ε P 2 para P* ε Ejemplo: (b (aba + ε) a)* 1 3 5 b a b 2 (b (aba + ε) a)* 4 (b (aba + ε) a)* 6 (b (aba + ε) a)*

Expresiones Regulares 7 10 3 a 4 a a ε 8 (b (aba + ε) a)* 9 (b (aba + ε) a)* 11 (b (aba + ε) a)* 5 b 8 a 6 ε 7 (b (aba + ε) a)*

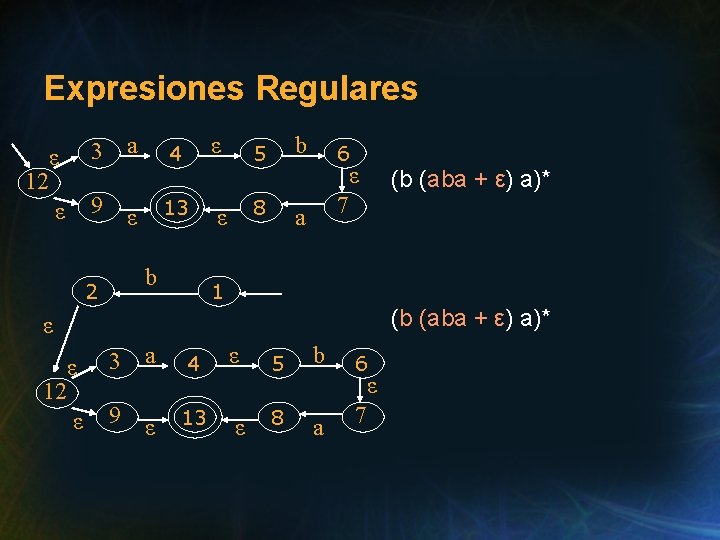
Expresiones Regulares ε 3 ε 9 12 a ε 4 13 ε b 2 b 5 ε 8 ε 6 (b (aba + ε) a)* 7 a 1 (b (aba + ε) a)* ε ε 12 ε 3 a 9 ε 4 ε 13 ε 5 b 8 a 6 ε 7

Expresiones Regulares b 2 1 (b (aba + ε) a) * ε ε 12 ε 11 3 a 9 ε a 10 4 ε 13 ε ε 5 b 8 a 6 ε 7

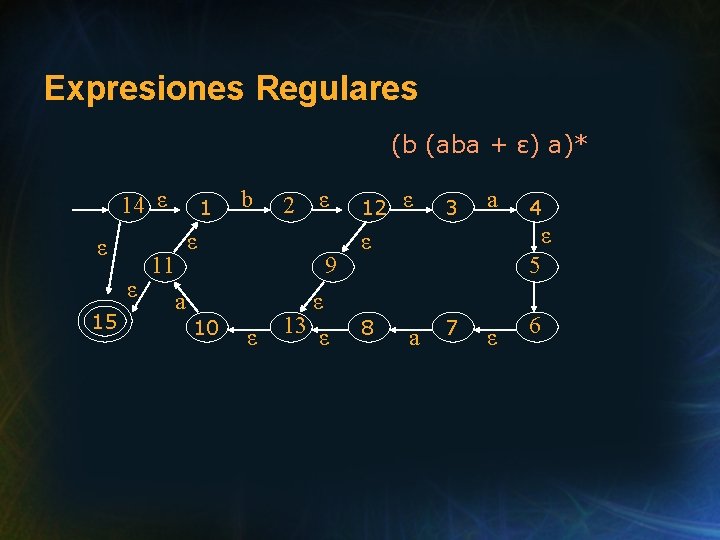
Expresiones Regulares (b (aba + ε) a)* 14 ε ε ε 15 1 b ε 11 ε 9 a 10 2 ε ε 13 ε 12 ε 3 a ε ε 8 4 5 a 7 ε 6

Expresiones Regulares Algoritmo 6 (Versión 2): Expresión Regular → FSA (Autómata Finito no-determinístico) Punto de inicio: E

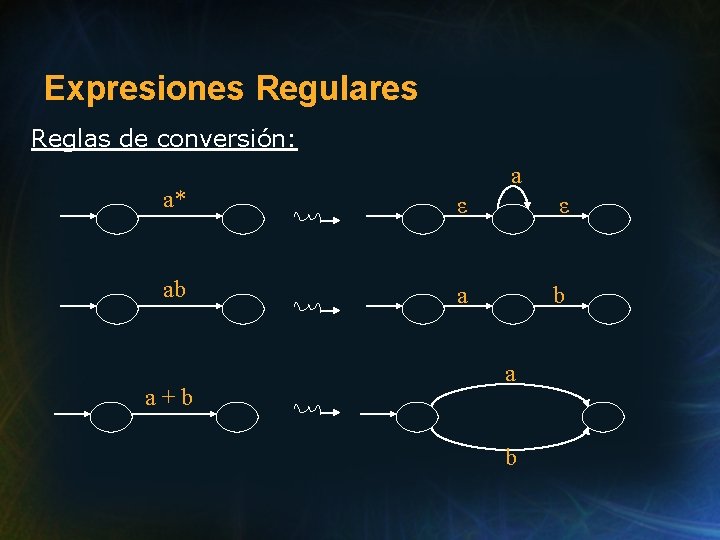
Expresiones Regulares Reglas de conversión: a a* ε ε ab a b a+b a b

Expresiones Regulares Algoritmo 6 versión 1: • Construye FSA de abajo hacia arriba • Bueno para máquinas • Malo para seres humanos Algoritmo 6 versión 2: • Construye FSA de arriba hacia abajo • Malo para máquinas • Bueno para seres humanos

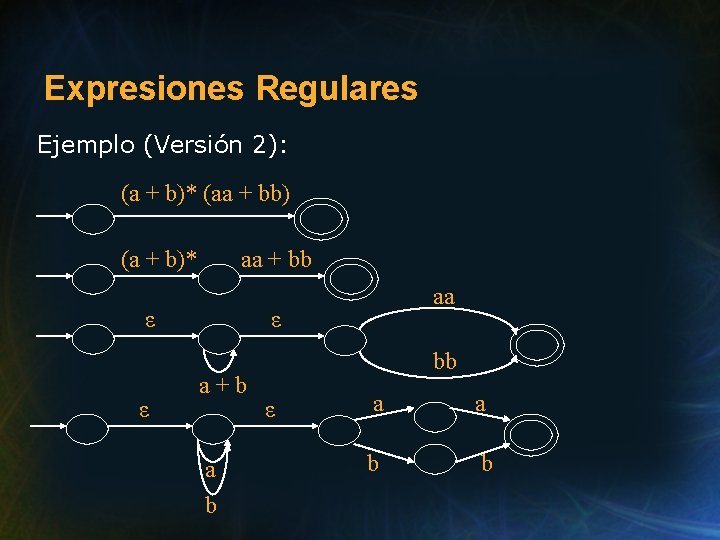
Expresiones Regulares Ejemplo (Versión 2): (a + b)* (aa + bb) (a + b)* aa + bb ε ε aa ε a+b a b bb ε a a b b

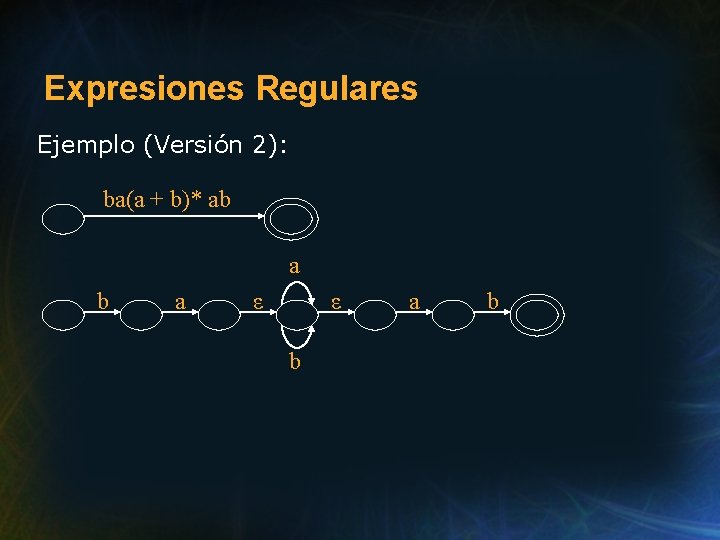
Expresiones Regulares Ejemplo (Versión 2): ba(a + b)* ab a ε ε b a b

Lenguajes Regulares Resumiendo: Listo RGR RGL Algoritmos 1, 2 Algoritmos 3, 4 Pronto DFA Mínimo Algoritmo 5 RE Algoritmo 6 NFA DFA

Autómatas de Estado Finito Determinísticos (DFA’s) Definición: Un FSA determinístico se define igual que uno no-determinístico, excepto que δ: Q x Σ → Q, en lugar de δ: Q x Σ U {ε} → 2 Q Así, ε y a a son impossibles.

Autómatas de Estado Finito Determinísticos (DFA’s) Cada transición de un DFA consume un símbolo. Afortunadamente, los DFA’s tiene el mismo poder (de reconocimiento) que los NFA’s. Teorema: Para cada NFA existe un DFA equivalente (i. e. que acepta el mismo lenguaje).

Autómatas de Estado Finito Determinísticos (DFA’s) Algoritmo 7: Conversión de NFA a DFA: • Se “simulan” las transiciones del NFA, con el DFA. • El estado inicial del DFA es el estado inicial del NFA (digamos, S), junto con todos los estados alcanzables (con ε) desde S. • Cada estado del DFA es un subconjunto de los estados del NFA. • Estados nuevos en el DFA se construyen calculando el conjunto de estados alcanzables desde estados del NFA, para cada símbolo. • Los estados finales del DFA son los que contienen al menos un estado final del NFA.

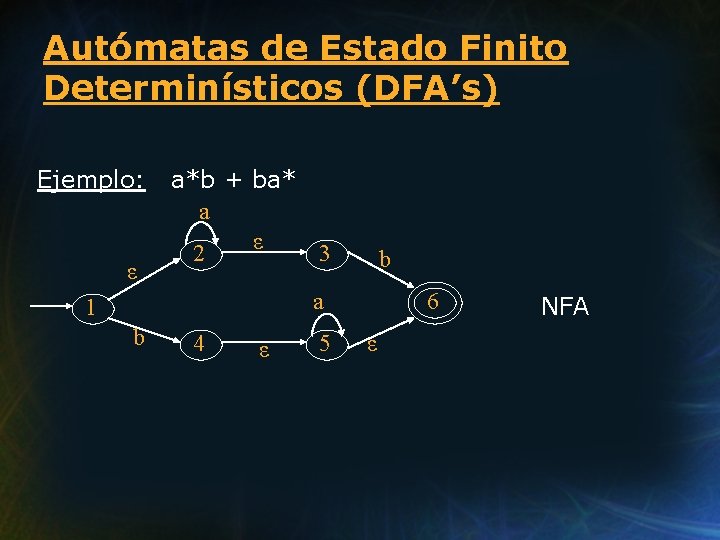
Autómatas de Estado Finito Determinísticos (DFA’s) Ejemplo: ε a*b + ba* a ε 2 3 b a 1 b 4 ε 5 6 ε NFA

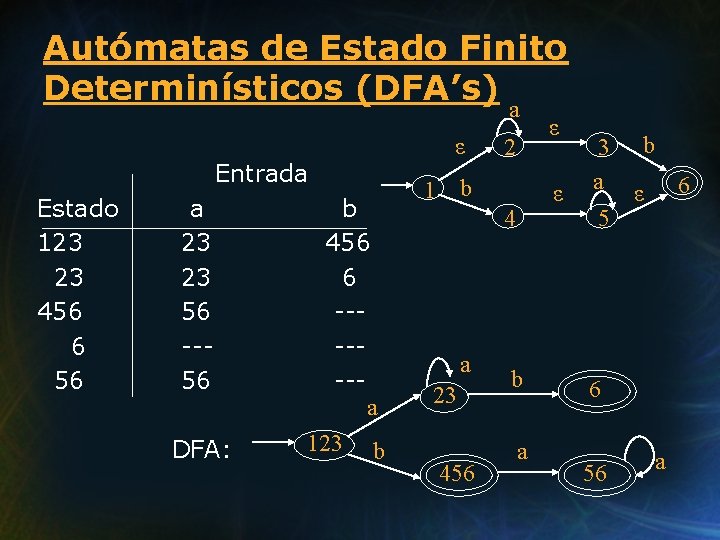
Autómatas de Estado Finito Determinísticos (DFA’s) a Entrada Estado 123 23 456 6 56 a 23 23 56 --56 DFA: b 456 6 ------a 123 b ε ε 2 1 b ε 4 a 23 456 b a 3 b a ε 6 56 a

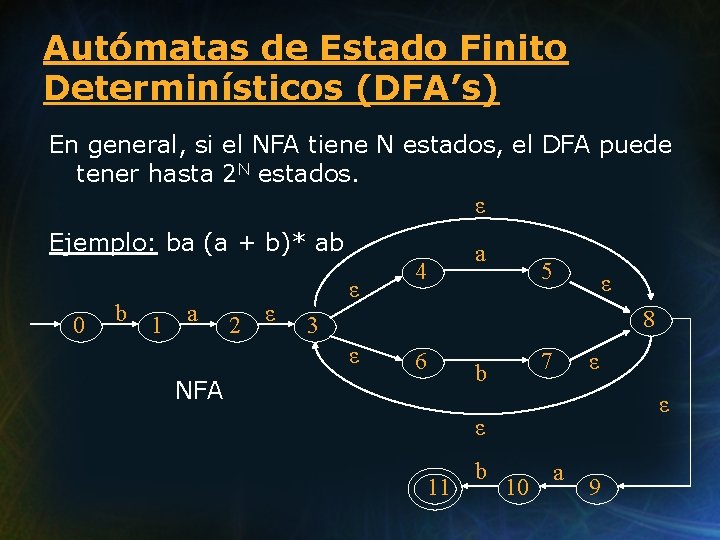
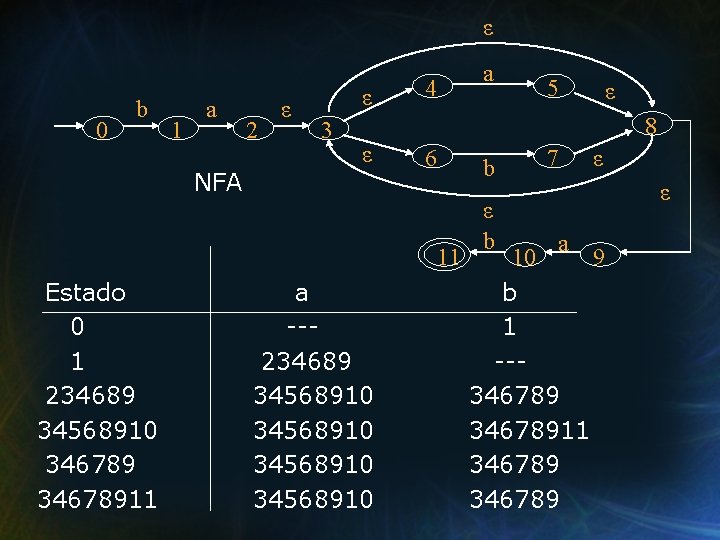
Autómatas de Estado Finito Determinísticos (DFA’s) En general, si el NFA tiene N estados, el DFA puede tener hasta 2 N estados. ε Ejemplo: ba (a + b)* ab 0 b 1 a 2 ε ε a 4 5 ε 8 3 ε 6 7 b NFA ε ε ε 11 b 10 a 9

ε 0 b 1 a NFA 2 ε ε 3 4 5 ε 8 ε 6 11 Estado 0 1 234689 34568910 34678911 a a --234689 34568910 b ε b 7 ε ε a 10 9 b 1 --34678911 346789

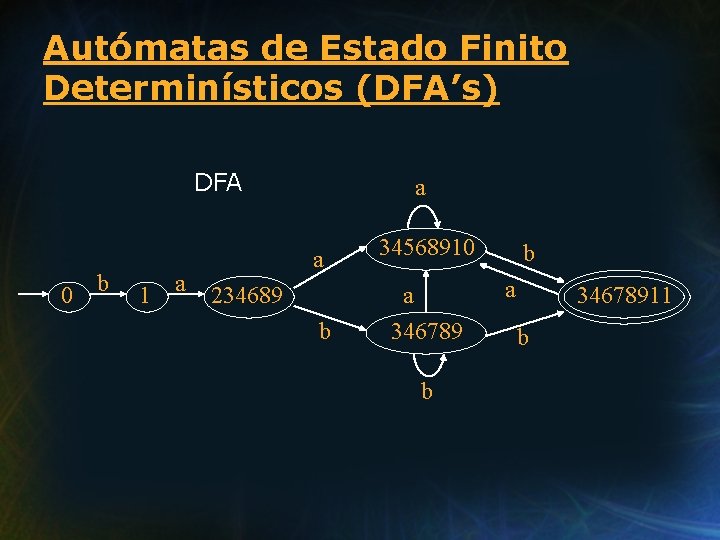
Autómatas de Estado Finito Determinísticos (DFA’s) DFA 0 b 1 a a a 34568910 b a 346789 234689 b b a 34678911 b

Lenguajes Regulares Resumiendo: Listo RGR RGL Algoritmos 1, 2 Algoritmos 3, 4 Pronto DFA Mínimo Algoritmo 5 RE Algoritmo 6 NFA Algoritmo 7 DFA

Minimización de Estados Teorema: Dado un DFA M, existe un DFA M’ equivalente que es mínimo, i. e. no existe ningún otro DFA equivalente con menos estados que M’. Definición: Una partición de un conjunto S es un conjunto de subconjuntos de S, tal que cada elemento de S aparece en uno (y solo uno) de esos subconjuntos.

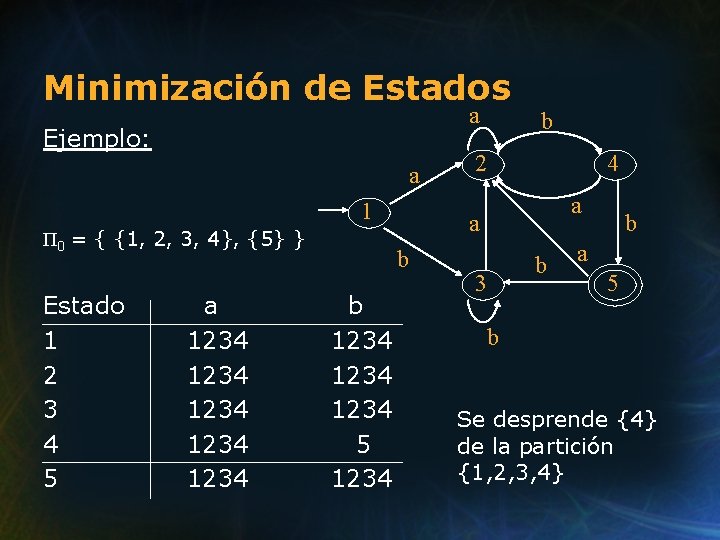
Minimización de Estados Ejemplo: S = {1, 2, 3, 4, 5} Π 1 = { {1, 2, 3, 4}, {5} } Π 2 = { {1, 2, 3, }, {4}, {5} } Π 3 = { {1, 3}, {2}, {4}, {5} } Nota: Π 2 es un refinamiento de Π 1 , y Π 3 es un refinamiento de Π 2.

Minimización de Estados Algorithmo 8 (Minimización de un DFA): 1. Eliminar las transiciones indefinidas introduciendo el estado TRAMPA, desde el cual no se llega un estado final. 2. Particionar los estados en dos grupos (finales y nofinales). 3. Completar la tabla de estados, especificando las transiciones de cada grupo a otros. Refinar la partición: se desprenden los grupos con transiciones distintas. 4. Repetir el paso 3 hasta no haber más refinamientos. 5. Determinar los estados finales.

Minimización de Estados a Ejemplo: a 1 Π 0 = { {1, 2, 3, 4}, {5} } Estado 1 2 3 4 5 a 1234 1234 2 4 a a b b 1234 5 1234 b b 3 b a 5 b Se desprende {4} de la partición {1, 2, 3, 4}

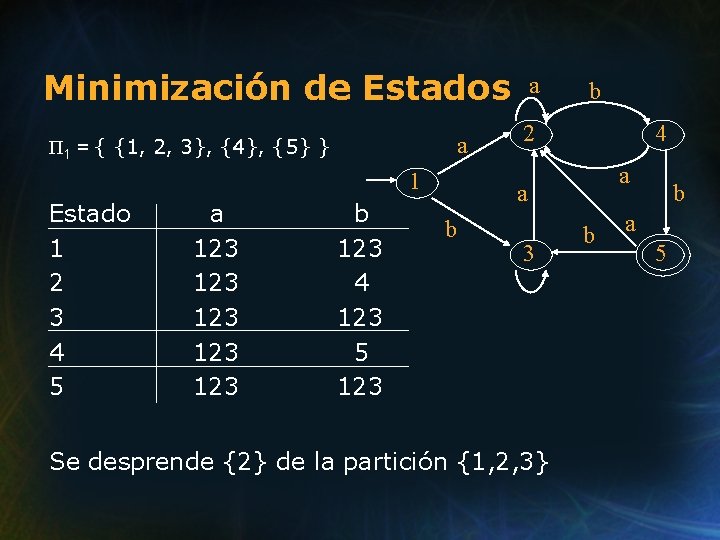
Minimización de Estados a Π 1 = { {1, 2, 3}, {4}, {5} } 1 Estado 1 2 3 4 5 a 123 123 123 b 123 4 123 5 123 a b 2 4 a a b 3 Se desprende {2} de la partición {1, 2, 3} b b a 5

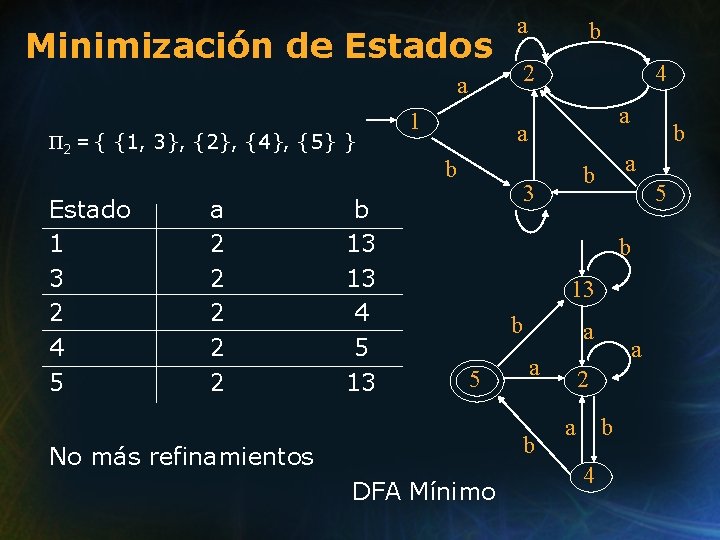
Minimización de Estados a 2 a Π 2 = { {1, 3}, {2}, {4}, {5} } Estado 1 3 2 4 5 a 2 2 2 b 13 13 4 5 13 1 b 4 a a b 3 b 5 b 13 b 5 a a b No más refinamientos DFA Mínimo a 2 a b 4

Lenguajes Regulares Resumiendo: RGR RGL Algoritmos 1, 2 Algoritmos 3, 4 Algoritmo 8 Algoritmo 5 RE DFA Mínimo Algoritmo 6 Listo ! NFA Algoritmo 7 DFA

Resumen de Lenguajes Regulares • La clase más pequeña de la jerarquía de Chomsky. • Apropiada para el análisis léxico. • Cuatro representaciones: RGR, RGL, ER y FSA. • Las cuatro son equivalentes (algoritmos de transformación). • Diversas ventajas y desventajas entre las cuatro representaciones, para el diseñador, el implementador, y el usuario de un lenguaje. • Los FSA se pueden hacer determinísticos y mínimos.
 Curso expresiones regulares
Curso expresiones regulares Curso de compiladores
Curso de compiladores Expresiones regulares
Expresiones regulares Simplificacion de expresiones regulares
Simplificacion de expresiones regulares Compiladores
Compiladores Ass compilación
Ass compilación Compiladores
Compiladores Dois recipientes
Dois recipientes Dom preparado
Dom preparado Quando voce se levantou pela manha eu ja havia preparado
Quando voce se levantou pela manha eu ja havia preparado Preparate para el encuentro con tu dios
Preparate para el encuentro con tu dios Preparado extemporaneo
Preparado extemporaneo Preprate
Preprate Que es un preparado magistral
Que es un preparado magistral Ejemplos de dictados
Ejemplos de dictados Que es un preparado magistral
Que es un preparado magistral Definicio
Definicio Escondidas es un verbo
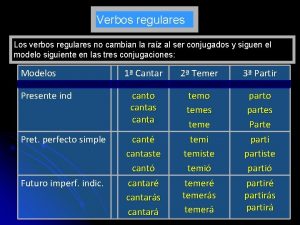
Escondidas es un verbo El imperfecto verbos regulares
El imperfecto verbos regulares Formulas de poliedros regulares e irregulares
Formulas de poliedros regulares e irregulares Polgono
Polgono Hexaedro
Hexaedro Verbos regulares condicional
Verbos regulares condicional Comparativos regulares
Comparativos regulares Cuales son los poliedros platonicos
Cuales son los poliedros platonicos Reglas verbos regulares en ingles
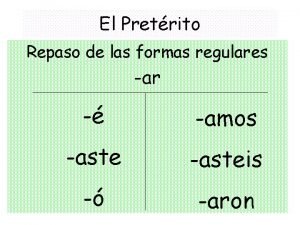
Reglas verbos regulares en ingles Prterito
Prterito Textura naturais
Textura naturais Imperativo familiar formas regulares
Imperativo familiar formas regulares Acostarse mandato
Acostarse mandato Cuáles son los verbos regulares e irregulares
Cuáles son los verbos regulares e irregulares Embaldosar el plano
Embaldosar el plano What are cognates
What are cognates Cuales son los poliedros platonicos
Cuales son los poliedros platonicos Nomenclatura de poligonos
Nomenclatura de poligonos Tomar imperativo afirmativo
Tomar imperativo afirmativo Noticiou o suplemento agricola do jornal
Noticiou o suplemento agricola do jornal Las formas regulares
Las formas regulares Unus duo tres nihil
Unus duo tres nihil 10 vervos regulares
10 vervos regulares Cuadro comparativo de verbos regulares e irregulares
Cuadro comparativo de verbos regulares e irregulares Teselados regulares e irregulares
Teselados regulares e irregulares Cognados regulares
Cognados regulares Verbos ar regulares
Verbos ar regulares