CES41 COMPILADORES Captulo Extra Compiladores Paralelos Captulo Extra

CES-41 COMPILADORES Capítulo Extra Compiladores Paralelos

Capítulo Extra Compiladores Paralelos E. 1 – Linguagens para processamento paralelo E. 2 – Componentes de um compilador paralelo E. 3 – Análise de dependências de dados E. 4 – O processo de paralelização de programas

E. 1 – Linguagens para processamento paralelo E. 1. 1 - Conceito de processamento paralelo n Supercomputadores: computadores com milhares de processadores e milhares de módulos de memória n Multiprocessamento: execução simultânea de vários programas n Processamento paralelo: execução simultânea de vários trechos de um mesmo programa

E. 1. 2 - Alternativas para linguagens n As linguagens utilizadas em processamento paralelo se classificam em: – – – n Linguagens paralelas Linguagens convencionais ampliadas Linguagens sequenciais Linguagens paralelas e convencionais ampliadas: – – – Exigem recodificação de todos os programas sequenciais de interesse, escritos até hoje Há mais de 50 anos de programação sequencial Obrigam muitos cientistas e pesquisadores a aprendê-las

n Linguagens sequenciais: alternativa muito pesquisada na programação de computadores paralelos: – n Desobrigam do aprendizado de novas linguagens (inércia dos cientistas e pesquisadores) A utilização de linguagens sequenciais em máquinas paralelas exigem do compilador a detecção automática de paralelismo dos programas

n Outras utilidades da detecção automática de paralelismo: – Em linguagens paralelas, para descobrir paralelismo não explícito pelo programador – Quanto menor o nível de paralelismo, mais difícil expressá-lo (iterações paralelas de laços, comandos paralelos internos às iterações, paralelismo intracomandos) – Para adequar o paralelismo dos programas ao potencial de paralelismo da máquina

E. 1. 3 - Paralelismo em programas sequenciais E. 1. 3 - n Programas sequenciais apresentam muito paralelismo implícito – n Uma das maiores fontes de paralelismo é o laço sequencial Exemplos: 1) C 1: C 2: for (i 1; i 5; i++) { A[i] B[i] + C[i]; D[i] E[i] + F[i]; } Todas as instâncias de C 1 e de C 2 podem ser executadas simultaneamente

2) C 1: C 2: for (i 1; i 5; i++) { A[i] B[i] + C[i]; D[i] A[i] + E[i]; } C 1[1] C 1[2] C 1[3] C 1[4] C 1[5] C 2[1] C 2[2] C 2[3] C 2[4] C 2[5] Todas as iterações podem ser executadas simultaneamente

n Alguns laços não apresentam paralelismo n Exemplo: C 1: C 2: for (i 1; i 5; i++) { A[i] B[i] + C[i]; B[i+1] A[i] + D[i]; } C 1[1] C 1[2] C 1[3] C 1[4] C 1[5] C 2[1] C 2[2] C 2[3] C 2[4] C 2[5] Há dependências intra e inter iterações As iterações e os seus comandos internos são sequenciais

n Há comandos a princípio sequenciais, mas que podem ser transformados de forma a apresentar paralelismo n Exemplo: seja o seguinte laço: C 1: C 2: for (i 1; i 5; i++) { A[i] B[i] + C[i]; D[i] A[i] + A[i+1]; } C 1[1] C 1[2] C 1[3] C 1[4] C 1[5] C 2[1] C 2[2] C 2[3] C 2[4] C 2[5] Há uma dependência de fluxo de C 1[i] para C 2[i] e uma antidependência de C 2[i] para C 1[i+1]

n Há comandos a princípio sequenciais, mas que podem ser transformados de forma a apresentar paralelismo n Exemplo: seja o seguinte laço: C 1: C 2: for (i 1; i 5; i++) { A[i] B[i] + C[i]; D[i] A[i] + A[i+1]; } C 1[1] C 1[2] C 1[3] C 1[4] C 1[5] C 2[1] C 2[2] C 2[3] C 2[4] C 2[5] Novamente as iterações e os comandos delas internos são sequenciais

C 1: C 2: for (i 1; i 5; i++) { A[i] B[i] + C[i]; D[i] A[i] + A[i+1]; } No entanto, pode-se alterar o escopo do laço de forma a introduzir nele paralelismo: C 2’: C 1: C 2: for (i 1; i 5; i++) { T[i] A[i+1]; A[i] B[i] + C[i]; D[i] A[i] + T[i]; } O laço pode ser decomposto em dois:

C 2’: C 1: C 2: n for (i 1; i 5; i++) T[i] A[i+1]; for (i 1; i 5; i++) { A[i] B[i] + C[i]; D[i] A[i] + T[i]; } Em cada laço, todas as iterações podem ser executadas simultaneamente Assim, um compilador de uma linguagem sequencial para processamento paralelo deve fazer: – Análise de dependências do programa fonte – Transformações no programa fonte, introduzindo-lhe mais paralelismo

E. 2 – Componentes de um compilador paralelo n Grosso modo, um compilador paralelo de linguagens sequenciais deve ter os seguintes componentes: 1. Analisador sintático e semântico, armazenando o programa fonte numa estrutura adequada 2. Construtor do grafo de dependências do programa, fonte de consultas para as transformações subsequentes 3. Eliminador de dependências e redutor de seus ciclos, visando aumentar o potencial de

E. 2 – Componentes de um compilador paralelo n Grosso modo, um compilador paralelo de linguagens sequenciais deve ter os seguintes componentes: 4. Reorganizador de laços, tornando-os tratáveis pelo passo 6 5. Alocador de memória, visando boa utilização de memória local e global 6. Paralelizador propriamente dito, transformando os comandos e laços sequenciais em equivalentes paralelos

E. 3 – Análise de Dependências de Dados E. 3. 1 – Tipos de dependências a) Dependência de fluxo: n Um comando produz um valor e outro o utiliza n Exemplo: C 1: A B + C; C 2: D A + E; Simbologia: a dependência é expressa por (C 1 f C 2)

b) Antidependência: n Um comando usa o valor de uma variável e outro o altera n Exemplo: C 1: A B + C; C 2: B D + E; Simbologia: a dependência é expressa por (C 1 a C 2)

c) Dependência de saída: n Um comando produz um valor para uma variável e depois outro lhe produz outro valor n Exemplo: C 1: A B + C; C 2: A D + E; Simbologia: a dependência é expressa por (C 1 s C 2)

d) Dependência condicional: n O resultado da condição de um comando determina se outro comando será ou não executado n Exemplo: C 1: if (A < B) C 2: C D + E; Simbologia: a dependência é expressa por (C 1 c C 2)

E. 3. 2 – Grafos de dependências n O conceito de dependência pode ser estendido para o escopo de laços n Exemplo: um laço e a lista de suas dependências: for (i 1; i n; i++) { C 1: a X[i] + X[i-1]; C 2: Z[i] a ** 2; C 3: X[i] X[i-1] + B[i]; } n Dependências: (C 1 s C 1) (C 1 f C 2) (C 1 a C 3) (C 2 a C 1) (C 3 f C 3) Concebe-se o grafo de dependências: nível de comandos, nível de instância e nível atômico

for (i 1; i n; i++) { C 1: a X[i] + X[i-1]; C 2: Z[i] a ** 2; C 3: X[i] X[i-1] + B[i]; } n Dependências: (C 1 s C 1) (C 1 f C 2) (C 1 a C 3) (C 2 a C 1) (C 3 f C 3) Nível de comandos: Todas as dependências estão num só ciclo; ciclos têm difícil solução paralela

for (i 1; i n; i++) { C 1: a X[i] + X[i-1]; C 2: Z[i] a ** 2; C 3: X[i] X[i-1] + B[i]; } n Nível de instâncias: Dependências: (C 1 s C 1) (C 1 f C 2) (C 1 a C 3) (C 2 a C 1) (C 3 f C 3)

for (i 1; i n; i++) { C 1: a X[i] + X[i-1]; C 2: Z[i] a ** 2; C 3: X[i] X[i-1] + B[i]; } n Nível atômico: Mostra os elementos de variáveis responsáveis pelas dependências Dependências: (C 1 s C 1) (C 1 f C 2) (C 1 a C 3) (C 2 a C 1) (C 3 f C 3)

E. 3. 3 – Definições para dependências n Existe uma dependência de dados (excluída a dependência condicional) de um comando C 1 para outro não necessariamente distinto C 2, simbolicamente (C 1 C 2), se e somente se existirem instâncias C 1’ e C 2’ de C 1 e C 2 e uma posição M de memória tais que: 1. C 1’ e C 2’ fazem referência a M e pelo menos uma dessas referências é uma escrita 2. C 1’ é executada antes de C 2’ 3. M não recebe escrita entre C 1’ e C 2’

1. C 1’ e C 2’ fazem referência a M e pelo menos uma dessas referências é uma escrita 2. C 1’ é executada antes de C 2’ 3. M não recebe escrita entre C 1’ e C 2’ n n C 1: fonte da dependência; C 1’: instância fonte C 2: destino da dependência; C 2’: instância destino n n n Dependência de fluxo: C 1’ é escrita e C 2’ é leitura em M Antidependência: C 1’ é leitura e C 2’ é escrita em M Dependência de saída: C 1’ e C 2’ são escritas em M Obs. : algumas referências bibliográficas incluem o item 3 apenas para as dependências de fluxo

1. C 1’ e C 2’ fazem referência a M e pelo menos uma dessas referências é uma escrita 2. C 1’ é executada antes de C 2’ 3. M não recebe escrita entre C 1’ e C 2’ n Item 1: C 1’ e C 2’ fazem referência a M: – Para variáveis escalares é trivial: basta referenciarem a mesma variável – Para variáveis indexadas não basta: é necessária uma análise de seus subscritos

1. C 1’ e C 2’ fazem referência a M e pelo menos uma dessas referências é uma escrita 2. C 1’ é executada antes de C 2’ 3. M não recebe escrita entre C 1’ e C 2’ n Item 2: C 1’ é executada antes de C 2’; seja o seguinte laço: for (j 1; j n; j++) { for (i 1; i n; i++) { C 2: D[i] A ** 2; A E[i] + F[i]; } C 1: A B[j] + C[j]; } A dependência (C 1 f C 2) existe Se o laço j não existisse a dependência não existiria

1. C 1’ e C 2’ fazem referência a M e pelo menos uma dessas referências é uma escrita 2. C 1’ é executada antes de C 2’ 3. M não recebe escrita entre C 1’ e C 2’ n Item 3: M não recebe escrita entre C 1’ e C 2’; seja o seguinte laço: for (i 1; i n; i++) { C 2: C[i] A ** 2; C 1: A D[i] + E[i]; F[i] A ** 3; C 3: A G[i] + H[i]; } A dependência (C 1 f C 2) não existe Se o comando C 3 fosse condicional, a dependência existiria

n Dentro de laços, dependências têm direção e distância n Exemplos: sejam os seguintes laços: 1) for (i 1; i n; i++) { C 1: A[i] B[i] + 5; C 2: C[i] A[i] * 2; } A dependência (C 1 f C 2) é interna à iteração i Direção: ‘=’ Distância: zero 2) for (i 1; i n; i++) { C 1: A[i] B[i] + 5; C 2: C[i] A[i-3] * 2; } A dependência (C 1 f C 2) vai da iteração i até a i+3 Direção: ‘<’ Distância: 3

n Dentro de laços, dependências têm direção e distância n Exemplos: sejam os seguintes laços: 3) for (i 1; i n; i++) for (j 1; j n; j++) { C 1: A[i, j] B[i, j] + C[i, j] ; C 2: D[i, j] A[i-2, j+1] + E[i, j]; } A dependência (C 1 f C 2) vai da iteração (i, j) até a (i+2, j-1) Vetor-direção: (‘<’, ‘>’) Vetor-distância: (2, -1)

E. 3. 4 – Detecção de dependências n A detecção de dependências entre variáveis escalares pode utilizar análise de fluxo de dados aplicada em otimização de código, na construção de compiladores n Entre variáveis indexadas, além disso, é necessária uma análise dos subscritos dessas variáveis n Seja o aninhamento a seguir

for (I 1 P 1; I 1 Q 1; I 1 ++) { for (I 2 P 2; I 2 Q 2; I 2 ++) { Laços de C 1: I 1, I 2, . . . , Id+1, . . . , Ie for (Id Pd; Id Qd; Id ++) { for (Id+1 Pd+1; Id+1 Qd+1; Id+1 ++) { Laços de C 2: I 1, I 2, . . . , Id, Ie+1, . . . , In for (Ie Pe; Ie Qe; Ie ++) { C 1: . . . V[expr 1, 1, expr 1, 2, … , expr 1, m]. . . A dependência (C 1 C 2) } existe se e somente se existirem instâncias } for (Ie+1 Pe+1; Ie+1 Qe+1; Ie+1 ++) { C 1(i 1, i 2, . . . , id+1, . . . , ie) e C 2(j 1, j 2, . . . , jd, je+1, . . . , jn) for (In Pn; In Qn; In ++) { C 2: . . . V[expr 2, 1, expr 2, 2, … , expr 2, m]. . . tais que: } 1. k | (1 k m), expr 1, k = expr 2, k } 2. k | (1 k n), Pk ik, jk Qk } 3. A instância de C 1 é executada antes da instância de C 2 } }

1. k | (1 k m), expr 1, k = expr 2, k 2. k | (1 k n), Pk ik, jk Qk 3. A instância de C 1 é executada antes da instância de C 2 Item 1: sistema de m equações com as incógnitas: i 1, i 2, . . . , id+1, . . . , ie, j 1, j 2, . . . , jd, je+1, . . . , jn Item 2 e 3: inequações com as mesmas incógnitas n Se esse sistema de equações e inequações tiver solução, a dependência existe; caso contrário, não existe n Quando esse sistema é linear a literatura apresenta vários métodos de solução

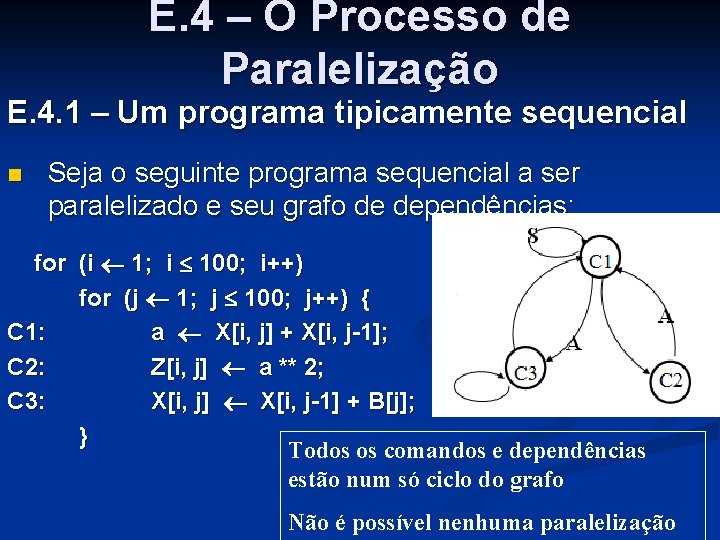
E. 4 – O Processo de Paralelização E. 4. 1 – Um programa tipicamente sequencial n Seja o seguinte programa sequencial a ser paralelizado e seu grafo de dependências: for (i 1; i 100; i++) for (j 1; j 100; j++) { C 1: a X[i, j] + X[i, j-1]; C 2: Z[i, j] a ** 2; C 3: X[i, j] X[i, j-1] + B[j]; } Todos os comandos e dependências estão num só ciclo do grafo Não é possível nenhuma paralelização

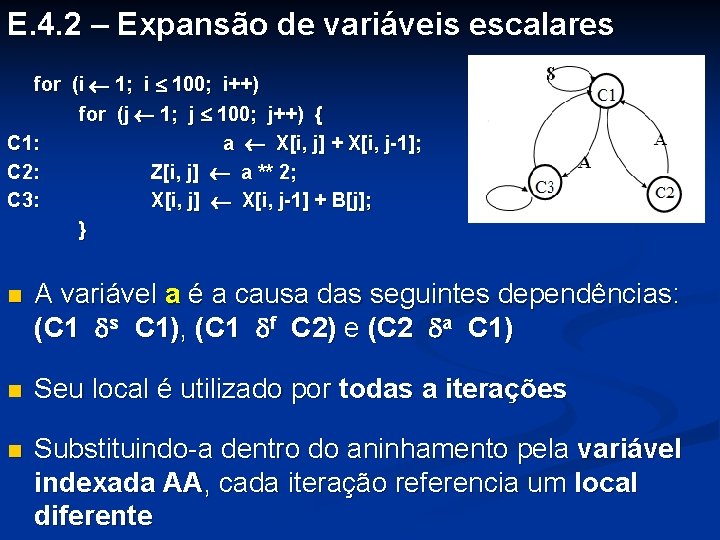
E. 4. 2 – Expansão de variáveis escalares for (i 1; i 100; i++) for (j 1; j 100; j++) { C 1: a X[i, j] + X[i, j-1]; C 2: Z[i, j] a ** 2; C 3: X[i, j] X[i, j-1] + B[j]; } n A variável a é a causa das seguintes dependências: (C 1 s C 1), (C 1 f C 2) e (C 2 a C 1) n Seu local é utilizado por todas a iterações n Substituindo-a dentro do aninhamento pela variável indexada AA, cada iteração referencia um local diferente

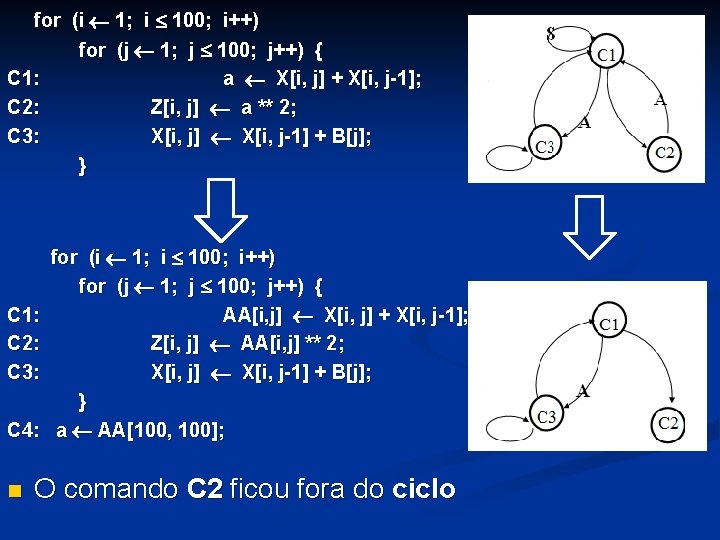
for (i 1; i 100; i++) for (j 1; j 100; j++) { C 1: a X[i, j] + X[i, j-1]; C 2: Z[i, j] a ** 2; C 3: X[i, j] X[i, j-1] + B[j]; } for (i 1; i 100; i++) for (j 1; j 100; j++) { C 1: AA[i, j] X[i, j] + X[i, j-1]; C 2: Z[i, j] AA[i, j] ** 2; C 3: X[i, j] X[i, j-1] + B[j]; } C 4: a AA[100, 100]; n O comando C 2 ficou fora do ciclo

E. 4. 3 – Reordenação de comandos de atribuição n Os comandos C 2 e C 3 podem trocar de posição: O comando C 4 foi omitido, mas será reconsiderado no final for (i 1; i 100; i++) for (j 1; j 100; j++) { C 1: AA[i, j] X[i, j] + X[i, j-1]; C 3: X[i, j] X[i, j-1] + B[j]; C 2: Z[i, j] AA[i, j] ** 2; } n O comando C 2 pode ser vetorizado

E. 4. 4 – Vetorização de laços n É a geração de comandos vetoriais for (i 1; i 100; i++) { for (j 1; j 100; j++) { C 1: AA[i, j] X[i, j] + X[i, j-1]; C 3: X[i, j] X[i, j-1] + B[j]; } C 2: Z[i, 1: 100] AA[i, 1: 100] ** 2 } n Os elementos Z[i, 1], Z[i, 2], . . . , Z[i, 100] podem ser calculados simultaneamente n O ciclo (C 1 C 3) pode ser quebrado

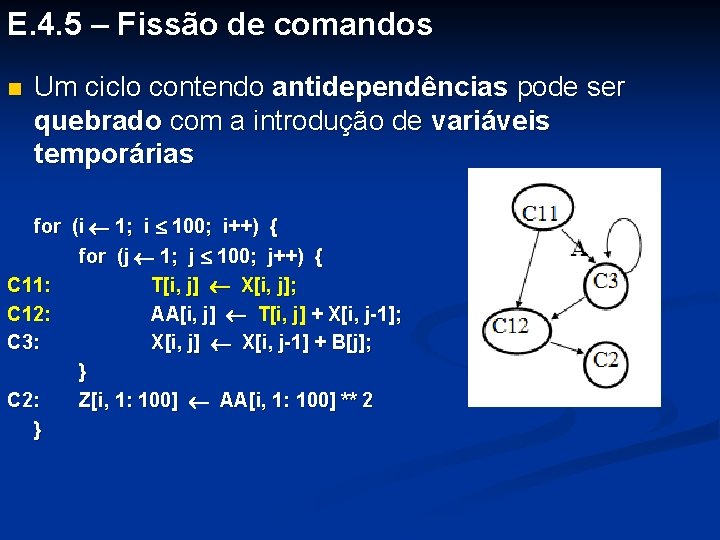
E. 4. 5 – Fissão de comandos n Um ciclo contendo antidependências pode ser quebrado com a introdução de variáveis temporárias for (i 1; i 100; i++) { for (j 1; j 100; j++) { C 1: C 3: C 2: } AA[i, j] X[i, j] + X[i, j-1]; X[i, j] X[i, j-1] + B[j]; } Z[i, 1: 100] AA[i, 1: 100] ** 2

E. 4. 5 – Fissão de comandos n Um ciclo contendo antidependências pode ser quebrado com a introdução de variáveis temporárias for (i 1; i 100; i++) { for (j 1; j 100; j++) { C 11: T[i, j] X[i, j]; C 12: AA[i, j] T[i, j] + X[i, j-1]; C 3: X[i, j] X[i, j-1] + B[j]; } C 2: Z[i, 1: 100] AA[i, 1: 100] ** 2 }

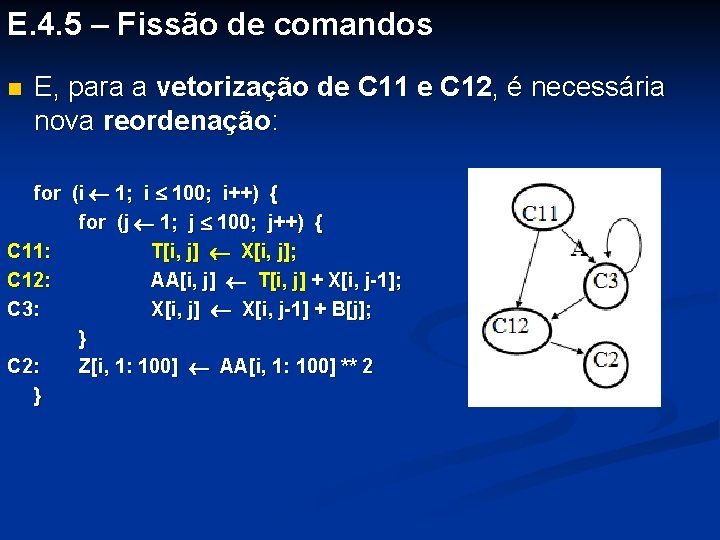
E. 4. 5 – Fissão de comandos n E, para a vetorização de C 11 e C 12, é necessária nova reordenação: for (i 1; i 100; i++) { for (j 1; j 100; j++) { C 11: T[i, j] X[i, j]; C 12: AA[i, j] T[i, j] + X[i, j-1]; C 3: X[i, j] X[i, j-1] + B[j]; } C 2: Z[i, 1: 100] AA[i, 1: 100] ** 2 }

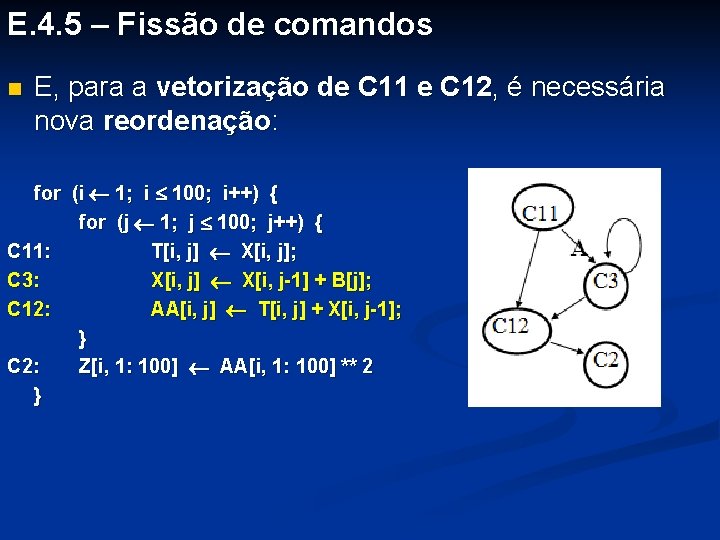
E. 4. 5 – Fissão de comandos n E, para a vetorização de C 11 e C 12, é necessária nova reordenação: for (i 1; i 100; i++) { for (j 1; j 100; j++) { C 11: T[i, j] X[i, j]; C 3: X[i, j] X[i, j-1] + B[j]; C 12: AA[i, j] T[i, j] + X[i, j-1]; } C 2: Z[i, 1: 100] AA[i, 1: 100] ** 2 }

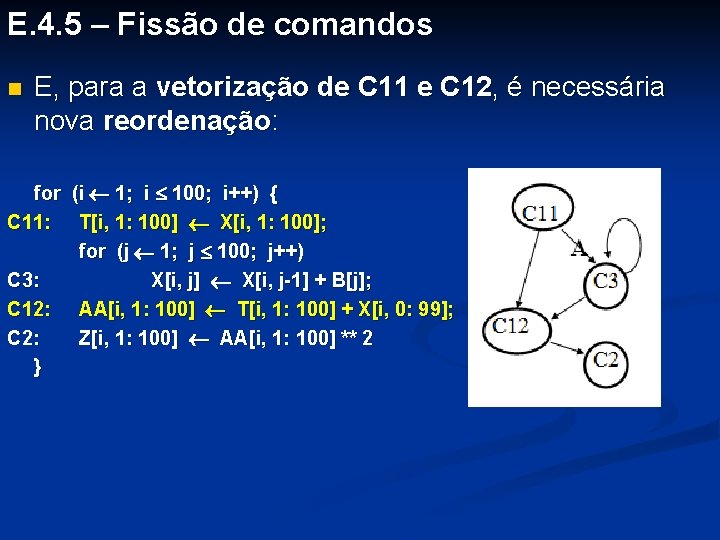
E. 4. 5 – Fissão de comandos n E, para a vetorização de C 11 e C 12, é necessária nova reordenação: for (i 1; i 100; i++) { C 11: T[i, 1: 100] X[i, 1: 100]; for (j 1; j 100; j++) C 3: X[i, j] X[i, j-1] + B[j]; C 12: AA[i, 1: 100] T[i, 1: 100] + X[i, 0: 99]; C 2: Z[i, 1: 100] AA[i, 1: 100] ** 2 }

E. 4. 6 – Decomposição parcial de laços n Um laço contendo vários comandos em seu escopo pode ser decomposto num conjunto de laços menores n Geralmente a paralelização de laços pequenos é mais simples que a de laços grandes n Assim o laço do programa anterior pode ser decomposto conforme o programa logo a seguir

E. 4. 6 – Decomposição parcial de laços C 11: for (i 1; i 100; i++) T[i, 1: 100] X[i, 1: 100]; C 3: for (i 1; i 100; i++) for (j 1; j 100; j++) X[i, j] X[i, j-1] + B[j]; C 12: C 2: n for (i 1; i 100; i++) { AA[i, 1: 100] T[i, 1: 100] + X[i, 0: 99]; Z[i, 1: 100] AA[i, 1: 100] ** 2; } Neste grafo de dependências, cada aninhamento tem seu grafo particular

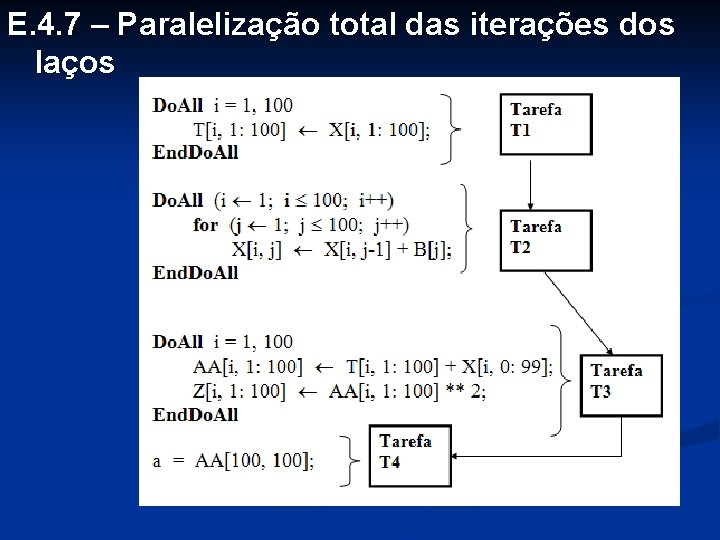
E. 4. 7 – Paralelização total das iterações dos laços n No programa anterior, os grafos do 1 o e do 3 o aninhamentos não apresentam ciclos n No grafo do 2 o aninhamento, a dependência é interna à iteração do laço externo (=, <) n Todos esses laços podem ser transformados em comandos Do. All, conforme o programa a seguir n Todas a iterações de um Do. All são executadas simultaneamente

E. 4. 7 – Paralelização total das iterações dos laços

E. 4. 9 – Resultado da paralelização n Resumindo o que foi feito, o comando sequencial, desprovido de paralelismo: for (i 1; i 100; i++) for (j 1; j 100; j++) { C 1: a X[i, j] + X[i, j-1]; C 2: Z[i, j] a ** 2; C 3: X[i, j] X[i, j-1] + B[j]; } n Foi transformado no programa paralelo a seguir

Do. All i = 1, 100 Suponha que este programa seja T[i, 1: 100] X[i, 1: 100]; executado numa máquina com 100 End. Do. All processadores e que cada um deles Do. All (i 1; i 100; i++) seja um processador matricial de for (j 1; j 100; j++) 100 processadores síncronos X[i, j] X[i, j-1] + B[j]; Tal máquina tem na realidade o End. Do. All equivalente a 10000 processadores Do. All i = 1, 100 escalares AA[i, 1: 100] T[i, 1: 100] + X[i, 0: 99]; Z[i, 1: 100] AA[i, 1: 100] ** 2; Suponha também, grosso modo, que cada comando de atribuição End. Do. All seja executado num tempo igual a a = AA[100, 100]; t unidades de tempo

Do. All i = 1, 100 T[i, 1: 100] X[i, 1: 100]; End. Do. All (i 1; i 100; i++) for (j 1; j 100; j++) X[i, j] X[i, j-1] + B[j]; A seguinte tabela mostra o tempo de execução do laço sequencial e End. Do. All das várias tarefas do programa Do. All i = 1, 100 paralelo AA[i, 1: 100] T[i, 1: 100] + X[i, 0: 99]; Z[i, 1: 100] AA[i, 1: 100] ** 2; End. Do. All a = AA[100, 100];

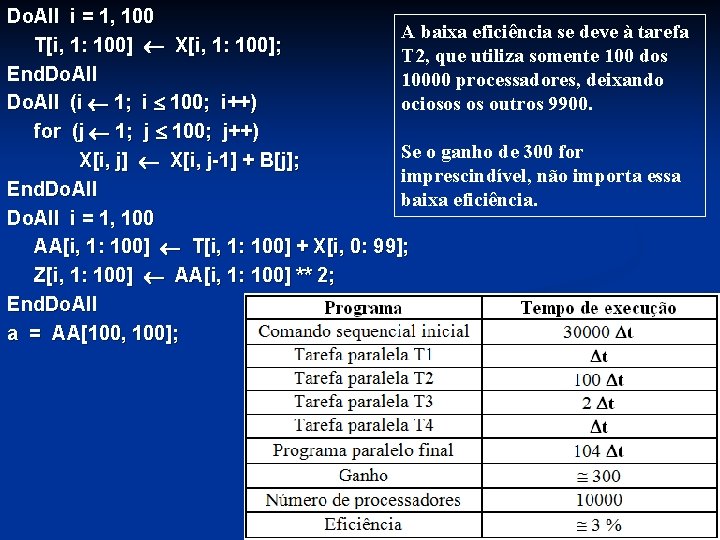
Do. All i = 1, 100 A baixa eficiência se deve à tarefa T[i, 1: 100] X[i, 1: 100]; T 2, que utiliza somente 100 dos End. Do. All 10000 processadores, deixando Do. All (i 1; i 100; i++) ociosos os outros 9900. for (j 1; j 100; j++) Se o ganho de 300 for X[i, j] X[i, j-1] + B[j]; imprescindível, não importa essa End. Do. All baixa eficiência. Do. All i = 1, 100 AA[i, 1: 100] T[i, 1: 100] + X[i, 0: 99]; Z[i, 1: 100] AA[i, 1: 100] ** 2; End. Do. All a = AA[100, 100];

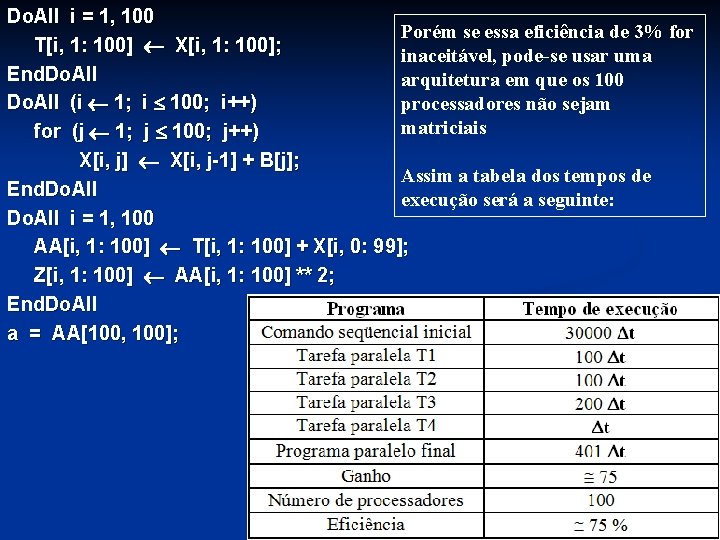
Do. All i = 1, 100 Porém se essa eficiência de 3% for T[i, 1: 100] X[i, 1: 100]; inaceitável, pode-se usar uma End. Do. All arquitetura em que os 100 Do. All (i 1; i 100; i++) processadores não sejam matriciais for (j 1; j 100; j++) X[i, j] X[i, j-1] + B[j]; Assim a tabela dos tempos de End. Do. All execução será a seguinte: Do. All i = 1, 100 AA[i, 1: 100] T[i, 1: 100] + X[i, 0: 99]; Z[i, 1: 100] AA[i, 1: 100] ** 2; End. Do. All a = AA[100, 100];