Identificando Linguagens No Regulares Linguagens regulares podem ser



































- Slides: 37

Identificando Linguagens Não Regulares • Linguagens regulares podem ser finitas; • Uma linguagem é regular sss, em processando qualquer cadeia, a informação a ser armazenada em qualquer estágio é estritamente limitada.

• Exemplo: A linguagem L={ an bn|n 0} não é regular. • Suponha que L é regular. Então existe um AFD M=(Q, {a, b}, S, q 0, F) que a reconhe-ce. Seja k o número de estados de M. Consideremos o funcionamento de M na entrada anbn, onde n k

aaaaabbbbb q 0 n n r • Como n k, deve existir algum estado p tal que M está em p mais de uma vez enquanto percorrendo a parte inicial da sequência de a’s (princípio da casa dos pombos).

• Quebre anbn em 3 pedaços u, v, w onde v é a cadeia de a’s percorrida entre duas ocorrências de p. aaaaaa q 0 u aaaa bbbbb p v p w r

• Seja j=|v|>0 (j=4, no exemplo) * (q 0, u) = p * (p, v) = p * (p, w) = r F • Logo podemos remover v o que resultaria numa cadeia ser erroneamente aceita:

*(q 0, uw) = *( *(q 0, u), w) = *(p, w) =r F aaaaaa q 0 u bbbbb p w r

Lema do Bombeamento (Pumping Lemma) TEOREMA: Seja L uma linguagem regular. Então existe um inteiro positivo m, tal que w L com |w| m pode ser decomposta como w= xyz com |xz| m e |y| 1 tal que wi=xyiz está também em L para todo i = 0, 1, 2, . . .

Prova • Sejam q 0, q 1, …, qn os estados do AFD que reconhece L. Agora tome uma cadeia w L tal que |w|=k m=n+1. • Seja q 0, qi, qj, … , qf o conjunto de estados do autômato no reconhecimento de w. Como esta cadeia tem no mínimo n+1 entradas, pelo menos um estado deve ser repetido, e tal repetição não deve começar após o n-ésimo movimento.

• Portanto, a sequência deve ter a seguinte forma q 0, qi, qj, … , qr, …, qf • indicando que devem existir subcadeias x, y, z de w tal que *(q 0, x)=qr, *(qr, y)=qr, *(qr, z)=qf com |xz| n+1 = m e |y| 1. • Donde segue imediatamente que *(q 0, xz)=qf, *(q 0, xy 2 z)=qf, *(q 0, xy 3 z)=qf. . . q. e. d

Gramáticas • Gramática uma ferramenta comum e poderosa para definir linguagens. • Definição: Uma gramática G é uma quádrupla G=(V, T, S, P) onde: – V é um conjto finito de variáveis ou símbolos não-terminais; – T é um conjunto finito de símbolos terminais; – S V é um símbolo especial chamado de símbolo inicial ou variável de início; – P é um conjunto finito de produções

• As regras de produção são da forma x y, onde x é um elemento de (V T)+ e y está em (V T)*. • As produções são aplicadas como segue: – dada uma cadeia w da forma w=uxv, dizemos que a produção é aplicável a esta cadeia e podemos usá-la para trocar x por y, obtendo assim uma nova cadeia z=uyv • Isto é escrito por w z (w deriva z ou z é derivada de w ou z deriva de w).

• Se w 1 w 2. . . wn, dizemos que w 1 deriva wn e escrevemos w 1 *wn • * indica que foi tomado um número não-especificado de etapas (incluindo zero) para derivar wn de w 1. Logo w *w sempre se dá. • Para indicar que pelo menos uma produção foi aplicada, escrevemos w +v

• Aplicando as regras de produção em ordens diferentes, uma gramática pode gerar muitas cadeias. O conjunto de todas tais cadeias é a linguagem definida ou gerada pela gramática.

Linguagem Gerada • Definição: Seja G = (V, T, S, P) uma gramática. Então o conjunto L(G) = {w T* | S *w} é a linguagem gerada por G. • Se w L (G), então a sequência S w 1 w 2 … wn w é uma derivação da sentença (ou palavra) w.

Exemplo • G = <{S}, {a, b}, S, P> onde P é dado por S a. Sb e S • Então S a. Sb aa. Sbb aabb • Logo podemos escrever S *aabb • Uma gramática define completamente L(G), porém pode não ser fácil obter uma descrição explícita da linguagem a partir da gramática. • Neste exemplo, no entanto, não é difícil conjecturar que L(G)={anbn|n 0}

Gramáticas Regulares • Uma gramática G = <V, T, S, P> diz-se linear à direita se todas as produções são da forma A x. B ou A x onde A, B V, e x T*. • e linear à esquerda se todas as produções são da forma A x. B A x

• Uma gramática regular é uma que é ou linear à direita ou linear à esquerda. • Observe que numa gramática regular no máximo aparece uma variável no lado direito de qualquer produção. Além disso, essa variável está mais à esquerda ou mais a direita de qualquer produção.

Exemplos • G 1 = ({s}, {a, b}, S, P 1), P 1: S ab. S|a é linear à direita. • S ab. S ababa • L (G 1) é a linguagem L((ab)*a) • G 2 = ({S, S 1, S 2}, {a, b}, S, P 2), com produções S S 1 ab, S 1 ab|S 2, S 2 a é linear à esquerda. • S S 1 abab S 2 abab aabab • L(G 2) é a linguagem L(a(ab)*)

Cuidado! A gramática G=({S, A, B}, {a, b}, S, P) com produções S A A a. B| B Ab não é regular!

Gramáticas Lineares À Direita Geram Linguagens Regulares • Construir um AFND que simula as derivações de uma gramática linear à direita. Ab…c. D Ab…cd. E por D d. E • O AFND vai do estado D para o estado E quando o símbolo d for encontrado.

Teorema. Seja G = (V, T, S, P) uma gramática linear à direita. Então L(G) é uma linguagem regular. Prova. Assumir V={V 0, V 1, …, Vp}, com S=V 0 e que temos produções da forma V 0 v 1 Vi, Vi v 2 Vj, …, ou Vn vl, …

• Se w é uma cadeia em L(G), então por causa das formas das produções em G, a derivação deve ter a forma da equação acima. V 0 v 1 Vi v 1 v 2 Vj * v 1 v 2… vk Vn v 1 v 2… v k v e = w

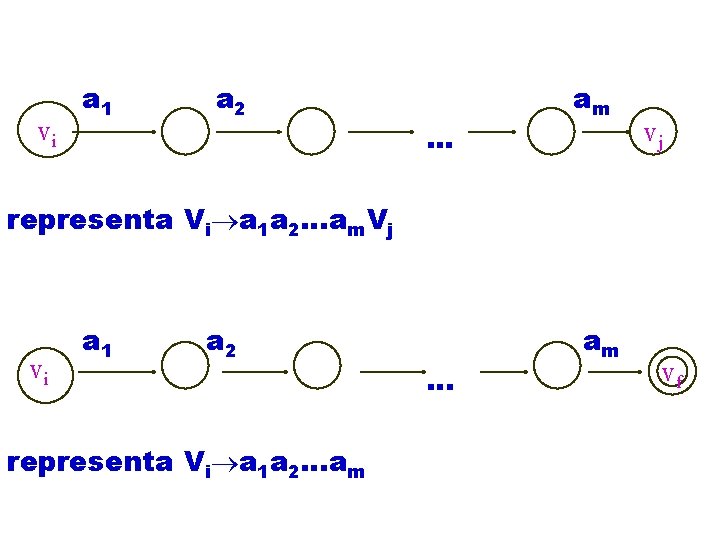
• O autômato a ser construído reproduzirá a derivação, consumindo cada um desses v’s. • O estado inicial do autômato será rotulado V 0, e para cada Vi existirá um estado não final rotulado Vi. • Para cada Vi a 1 a 2…am. Vj definiremos tal que *(Vi, a 1 a 2…am)=Vj • Para cada Vi a 1 a 2…am , *(Vi, a 1 a 2…am)=Vf, onde Vf é um estado final. Os estados intermediários não são de interesse e podem ser dados rótulos arbitrários.

vi a 1 a 2 . . . am vj representa Vi a 1 a 2…am. Vj vi a 1 a 2 representa Vi a 1 a 2…am … am vf

• Suponha agora que w L (G). No AFND existe uma aresta de V 0 a Vi rotulada v 1, de Vi a Vj rotulada v 2, etc. , tal que Vf *(V 0, w), e w é aceita por M. • Inversamente, suponha que w é aceita por M. Para aceitar w o autômato tem de passar pela sequência de estados V 0, Vi, …, Vf usando caminhos rotulados v 1, v 2, …, vl

• Portanto, w deve ter a forma w=v 1 v 2…vkvl e a derivação V 0 v 1 Vi v 1 v 2 Vj *v 1 v 2…vk. Vk v 1 v 2…vkvl é possível. Logo W está em L(G), e assim o teorema está provado.

Exemplo • Construir um autômato que aceita a linguagem gerada pela gramática V 0 a. V 1 ab. V 0 |b • começamos do grafo de transição com vértices V 0, V 1 e Vf.

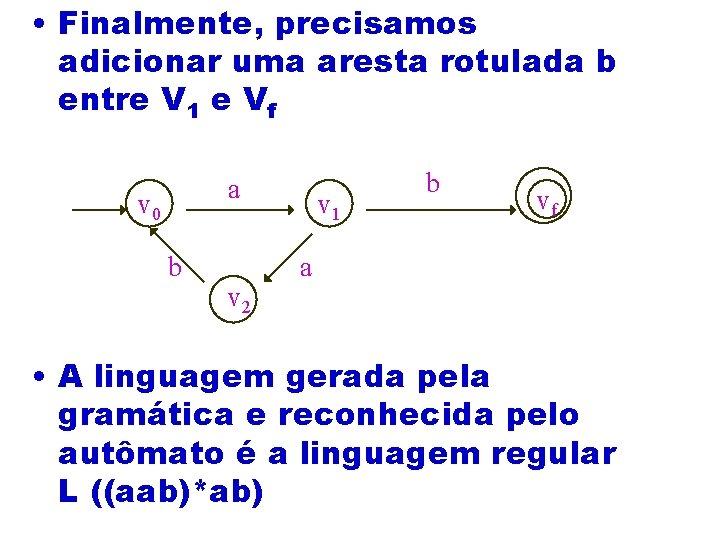
• A primeira regra de produção cria uma aresta rotulada a entre V 0 e V 1. Para segunda regra, precisamos introduzir um vértice adicional tal que existe um caminho rotulado ab entre V 1 e V 0.

• Finalmente, precisamos adicionar uma aresta rotulada b entre V 1 e Vf a v 0 b v 2 v 1 b vf a • A linguagem gerada pela gramática e reconhecida pelo autômato é a linguagem regular L ((aab)*ab)

Gramáticas Lineares À Direita Para Linguagens Regulares • Começamos agora do AFD para a linguagem e invertemos a construção do teorema anterior • Os estados do AFD tornam-se as variáveis da gramática, e • Os símbolos que causam as transições tornam-se os terminais nas produções

• Teorema: Se L é uma linguagem regular sobre o alfabeto , então existe uma gramática linear à direita G = (V, , S, P) tal que L = L(G).

• Prova: Seja M = (Q, , , q 0, F) um AFD que aceita L. Assumiremos que Q = {q 0, q 1, …, qn) e = {a 1, a 2, …am}. • Vamos construir uma gramática linear à direita G = (V, , S, P) com V = {q 0, q 1, …, qn} e S = q 0. • Para cada transição (qi, aj) = qk de M, colocamos em P a produção qi ajqk. • Além disso, se qk está em F, acrescentamos a P a produção q .

• Primeiro mostramos que G definida dessa maneira pode gerar toda cadeia em L. Considere w L da forma w = aiaj…akal. • Para M aceitar essa cadeia ele deve se movimentar via (q 0, ai) = qp, (qp, aj) = qr, . . . (qs, ak) = qt, (qt, al) = qf F

• Por construção, a gramática terá uma produção para cada um desses ’s. Portanto, podemos fazer a derivação q 0 aiqp aiajqr *aiaj…akqt aiaj…akalqf aiaj…akal com a gramática G, e w L(G).

• Inversamente, se w L(G), então sua derivação deve ter a forma da equação acima, mas isto implica que (q 0, ai, aj…akal) = qf, completando a prova. q. e. d.

Equivalência Entre Linguagens Regulares E Gramáticas Regulares • Os resultados anteriores estabelecem a conexão entre linguagens regulares e gramáticas lineares à direita. • Podemos fazer uma conexão análoga entre linguagens regulares e gramáticas lineares à esquerda, mostrando assim, a equivalência de gramáticas e linguagens regulares.

Teorema. Uma linguagem é regular se e somente se existe uma gramática regular G tal que L = L(G).
 Ser feliz não deve ser segredo deve ser sagrado
Ser feliz não deve ser segredo deve ser sagrado Par ordenado
Par ordenado Como os carboidratos podem ser classificados
Como os carboidratos podem ser classificados Tipos de linguagem
Tipos de linguagem Linguagens
Linguagens Slides cmsp
Slides cmsp Nacimos para ser felices no perfectos
Nacimos para ser felices no perfectos Ser espirita não é ser nenhum religioso
Ser espirita não é ser nenhum religioso El ser humano es un ser inacabado
El ser humano es un ser inacabado Queria ser poeta
Queria ser poeta Soy es eres
Soy es eres What is ser marketing
What is ser marketing Certas ondas podem sofrer amortecimento
Certas ondas podem sofrer amortecimento Podem algorithm
Podem algorithm Teselaciones cuadradas
Teselaciones cuadradas 10 verbos regular
10 verbos regular Cognate examples
Cognate examples El cilindro es regular o irregular
El cilindro es regular o irregular Reglas verbos regulares en ingles
Reglas verbos regulares en ingles Considere os seguintes poliedros regulares
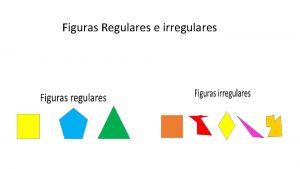
Considere os seguintes poliedros regulares Formas regulares
Formas regulares Imperativo en ingles ejemplos
Imperativo en ingles ejemplos Nombres de poliedros regulares
Nombres de poliedros regulares Expresiones regulares
Expresiones regulares Levantarse informal command
Levantarse informal command Teselaciones irregulares
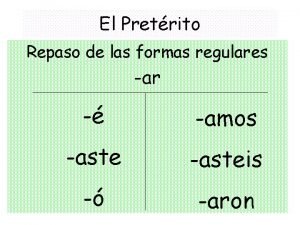
Teselaciones irregulares Los verbos ar
Los verbos ar False cognates examples
False cognates examples Imperativo familiar formas regulares
Imperativo familiar formas regulares Imperativo regulares
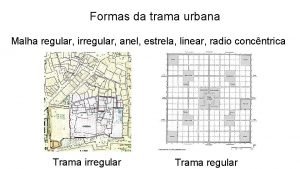
Imperativo regulares Trama urbana irregular
Trama urbana irregular Presente del modo indicativo
Presente del modo indicativo Expresiones regulares ejercicios resueltos
Expresiones regulares ejercicios resueltos Nomenclatura de poligonos
Nomenclatura de poligonos Que son verbos regulares e irregulares
Que son verbos regulares e irregulares Prterito imperfecto
Prterito imperfecto Oración es
Oración es El imperfecto verbos regulares
El imperfecto verbos regulares