Lenguajes Regulares Curso de Compiladores Preparado por Manuel

Lenguajes Regulares Curso de Compiladores Preparado por Manuel E. Bermúdez, Ph. D. Profesor Asociado University of Florida

Lenguajes Regulares Estudiaremos: • • • Gramáticas Regulares Relación con autómatas de estado finito Expresiones Regulares Equivalencia entre representaciones Eliminación del no-determinismo Minimización de estados

Lenguajes Regulares Definición: Una gramática G = (Φ, Σ, P, S) es regular sii una condición (pero no ambas): 1) Cada producción es de la forma A→ ó A → B (lineal derecha) 2) Cada producción es de la forma A→ or A → B (lineal izquierda) donde Σ*, y A, B Φ.

Lenguajes Regulares Ejemplos: G 1: S → a → b. U → b. R R→ → U→ → aba. U U b S G 2: S → a → Ub → Rb R → Uaba U →b → a. S ¿Regular? ¿ Por qué ? ¿ Regular? ¿ Por qué ?

Lenguajes Regulares => Diseñemos una máquina que acepte L(G 1). Observemos que S => a G 1: S → a R → aba. U => → b. U →U b. U => bb … → b. R U→b > => b. R = b. S … →S => baba. U 1. Toda forma sentencial (excepto las sentencias) tienen exactamente UN símbolo no-terminal. 2. El no-terminal ocurre en la posición derecha. 3. Producciones aplicables (derivaciones) dependen SOLO de ese no-terminal.

Lenguajes Regulares Estrategia: Representar todas la secuencias de derivación con la relación ”⊢” , sobre pares ordenados de la forma (q, ), donde q – el estado actual – la hilera que falta de aceptar Así, S → b. U implica (S, bβ) ⊢ (U, β) El estado “forma sentencial termina en S” “se transforma en” El estado “forma sentencial termina en U”

Lenguajes Regulares Así, (S, babab) ⊢ (R, abab) (porque S → b. R) ⊢ (U, b) (porque R → aba. U) ⊢ (ε, ε) (porque U → b) Criterio de aceptación de : (S, ) ⊢* (ε, ε)

Transformación de gramática regular a diagrama de transiciones: Definimos un grafo, con un nodo por cada noterminal, que describe las posibles acciones sobre cada forma sentencial. Así, S → b. U implica R → U implica S → a implica S R S b a U , y F .

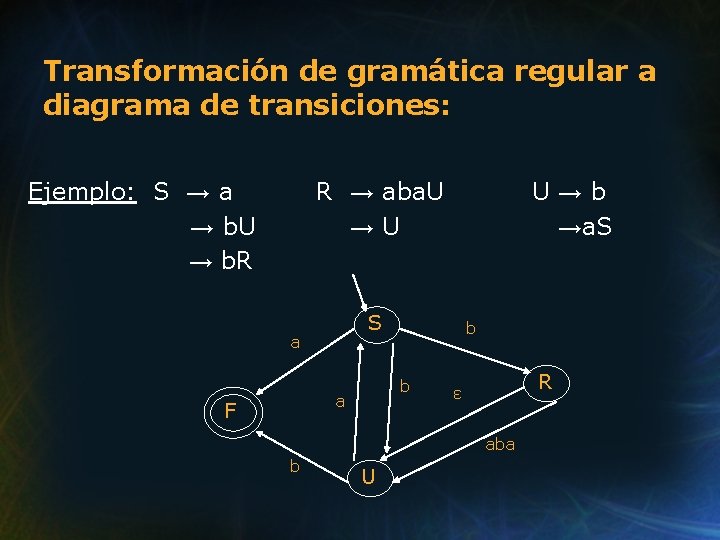
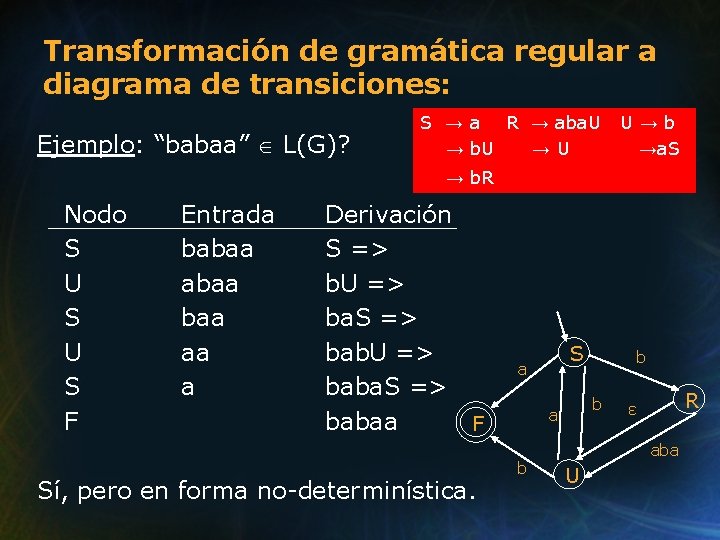
Transformación de gramática regular a diagrama de transiciones: Ejemplo: S → a → b. U → b. R R → aba. U →U S a b b a F U→b →a. S R ε aba b U

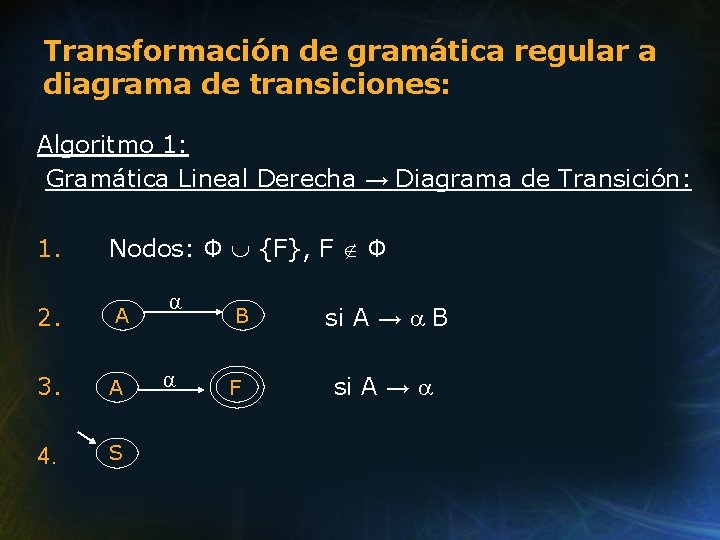
Transformación de gramática regular a diagrama de transiciones: Algoritmo 1: Gramática Lineal Derecha → Diagrama de Transición: 1. Nodos: Φ {F}, F Φ 2. A 3. A 4. S α α B F si A → B si A →

Transformación de gramática regular a diagrama de transiciones: Ejemplo: “babaa” L(G)? S → a R → aba. U → b. U →U U→b →a. S → b. R Nodo S U S F Entrada babaa baa aa a Derivación S => b. U => ba. S => bab. U => baba. S => babaa F Sí, pero en forma no-determinística. S a b b R ε aba U

Autómatas de Estado Finito Definición: Un autómata de estado finito (nodeterminístico) es una tupla M = (Q, Σ, δ, s, F), donde Q es un conjunto finito de estados, Σ es un conjunto finito de símbolos de transición, δ: Q x Σ U {ε} → 2 Q es una función parcial llamada la función de transición, s Q se llama el estado inicial, y F Q es el conjunto de estados finales. Un FSA es el mecanismo formal de aceptación de un lenguaje regular. Requiere que cada transición tenga una etiqueta (hilera) de longitud < 1.

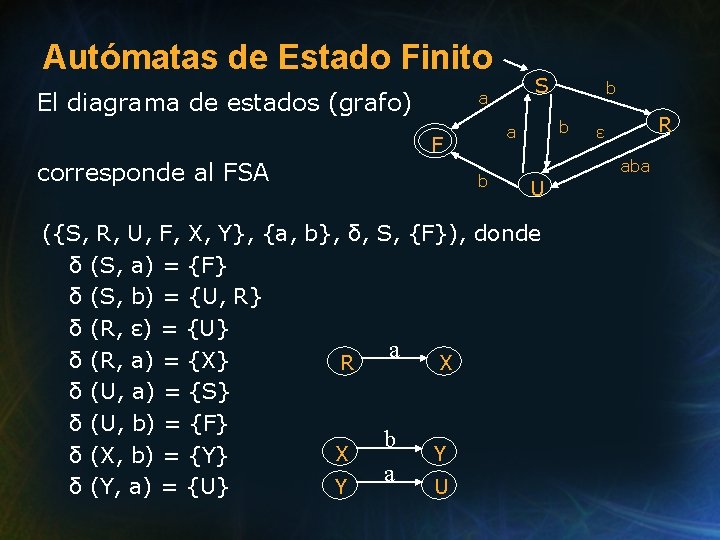
Autómatas de Estado Finito El diagrama de estados (grafo) corresponde al FSA b b a X Y U R ε aba U S, {F}), donde a b b a F ({S, R, U, F, X, Y}, {a, b}, δ, δ (S, a) = {F} δ (S, b) = {U, R} δ (R, ε) = {U} δ (R, a) = {X} R δ (U, a) = {S} δ (U, b) = {F} X δ (X, b) = {Y} Y δ (Y, a) = {U} S a

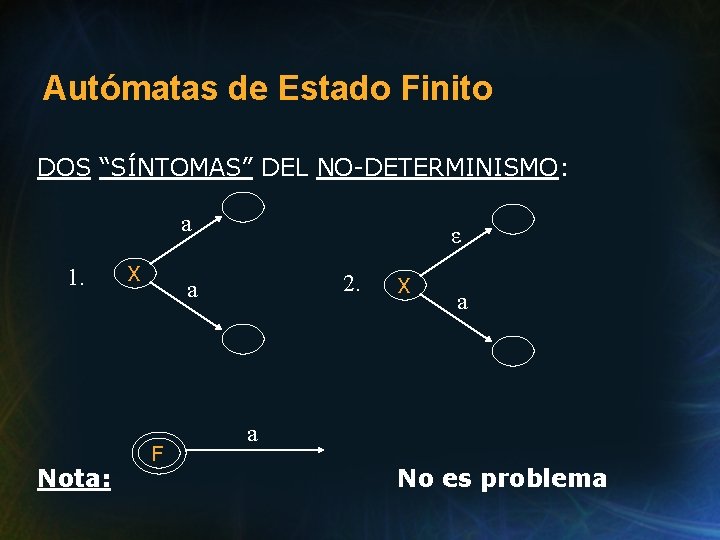
Autómatas de Estado Finito DOS “SÍNTOMAS” DEL NO-DETERMINISMO: a 1. Nota: X ε 2. a F X a a No es problema

Autómatas de Estado Finito Ventajas de los FSA’s: Pregunta: ¿ Qué lenguaje genera la siguiente gramática? S → a. A →ε C → b. D A → a. B →E D → b. E B → a. C →D E → b. S Difícil de visualizar. Intentemos el FSA.

Autómatas de Estado Finito ε F S a A E B ε ε b a b D a b C Respuesta: L*, donde L = {ab, aabb, aaabbb} Resumen: FSA’s son tan poderosas (en capacidad de reconocimiento) que las gramáticas lineales derechas. ¿ Son más poderosas ? No. Podemos transformar FSA → RGR.

Transformación de diagrama de transiciones a gramática regular Algoritmo 2: Diagrama de Transición → Gramática Lineal Derecha: 1. 2. 3. 4. Φ=Q A → a. B si B δ (A, a) A→a si f δ (A, a), y f F Símbolo de inicio = Estado inicial

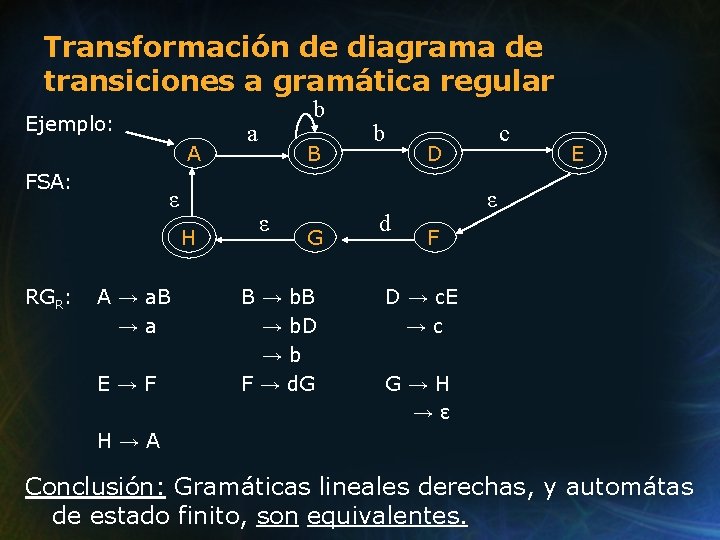
Transformación de diagrama de transiciones a gramática regular Ejemplo: A FSA: ε H RGR: A → a. B →a E→F b a B ε G B → b. D →b F → d. G b c D d E ε F D → c. E →c G→H →ε H→A Conclusión: Gramáticas lineales derechas, y automátas de estado finito, son equivalentes.

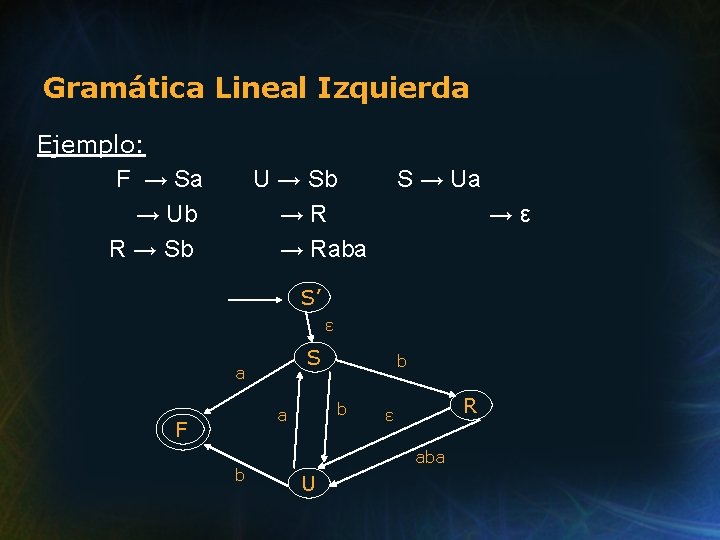
Gramática Lineal Izquierda Relación entre gramática lineal izquierda y FSA: Ejemplo: F → Sa → Ub U → Sb →R → Raba => => Derivaciones: Sbb. . . > = F => Ub => Rb. . . Rabab. . . Sa => Uaa. . . => a R → Sb S → Ua →

Gramática Lineal Izquierda Similaridades con gramáticas lineales derechas: 1. Formas sentenciales tienen a lo sumo un noterminal. 2. Sentencias no tienen no-terminales. 3. Producciones aplicables dependen solo del noterminal. Diferencias con gramáticas lineales derechas: 1. No-terminales aparecen a la izquierda. 2. La hilera se genera de derecha a izquierda, vs. de izquierda a derecha para gramáticas lineales derechas.

Gramática Lineal Izquierda Algoritmo 3: Gramática Lineal Izquierda → Diagrama de Transición 1. B 2. S’ α α A si A → B. si A → , S’ es un nuevo estado de inicio. 3. F = {S}, S es el símbolo de inicio. A

Gramática Lineal Izquierda Ejemplo: F → Sa → Ub R → Sb U → Sb →R → Raba S → Ua →ε S’ ε S a b a F b b R ε aba U

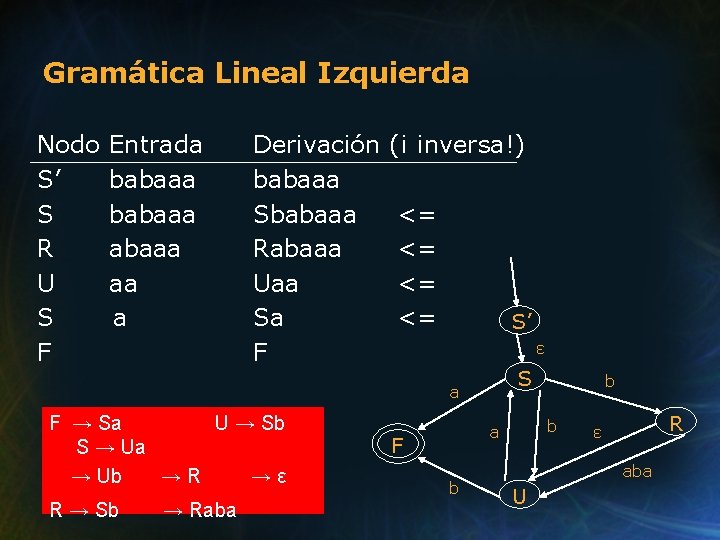
Gramática Lineal Izquierda Nodo S’ S R U S F Entrada babaaa aa a Derivación babaaa Sbabaaa Rabaaa Uaa Sa F (¡ inversa!) <= <= S’ ε S a F → Sa U → Sb S → Ua → Ub →R →ε R → Sb → Raba b a F b b R ε aba U

Gramática Lineal Izquierda Algoritmo 4: Diagrama de Transición → Gramática Lineal Izquierda: 1. A → B si B 2. A → si S 3. S’ → F si F α α A A Nuevo símbolo de inicio

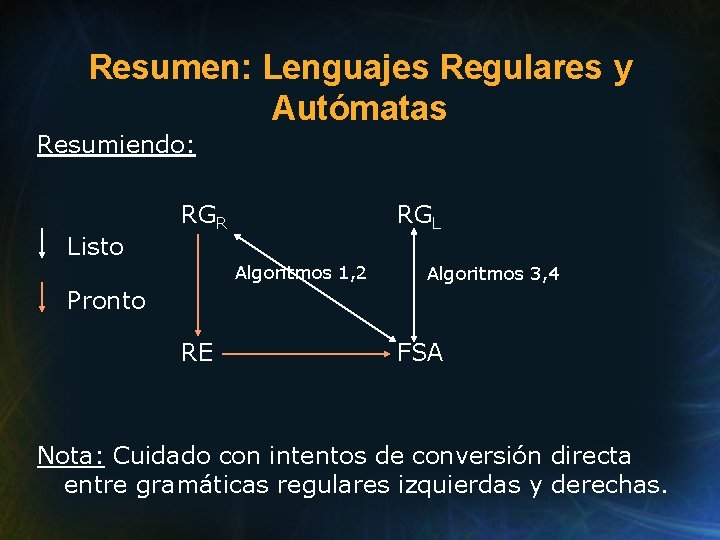
Resumen: Lenguajes Regulares y Autómatas Resumiendo: Listo RGR RGL Algoritmos 1, 2 Algoritmos 3, 4 Pronto RE FSA Nota: Cuidado con intentos de conversión directa entre gramáticas regulares izquierdas y derechas.