Sistemas Lineales Eloy Edmundo Rodrguez Vzquez Maestra en

Sistemas Lineales Eloy Edmundo Rodríguez Vázquez Maestría en Control Automático y Sistemas Dinámicos PICYT Clase 3

Calendario Junio 29 Julio 6 Julio 20 Julio 27 Agosto 3 Agosto 10 Agosto 17 Unidad 1 Presentaciones 7, 8, 9 y 10 Unidad 2 Presentaciones 11 y 12 Unidad 2 y 3 Presentaciones 14 y 13 Tarea 1 Unidad 4 Presentaciones 15 y 16 EXAMEN 1 (Unidades 1, 2 y 3) Unidad 5 Presentaciones 17 y 18 Unidad 6 Presentaciones 19 y 20 EXAMEN 2 (Unidades 4, 5 y 6) Tarea 2

Programa Unidad 1 Introducción a la representación de estados Unidad 2 Representación y análisis de los sistemas en espacios de estados Unidad 3 Control en espacio de estados Unidad 4 Síntesis de observadores Unidad 5 Control en espacio de estados implementado un observador Unidad 6 Espacio de estados de sistemas muestreados

Unidad 2 Representación y Análisis de los Sistemas en Espacio de Estados 2. 1 Ecuación de estado y función de transferencia. 2. 2 Descomposición canónica 2. 3 Formas canónicas de la representación de estado 2. 3. 1 La forma compañón para el control. 2. 3. 2 La forma modal. 2. 3. 3 La forma cascada. 2. 4 Conclusiones. 2. 4. 1 Interés de la representación de estado. 2. 4. 2 Traslado de una representación de estado a otra.

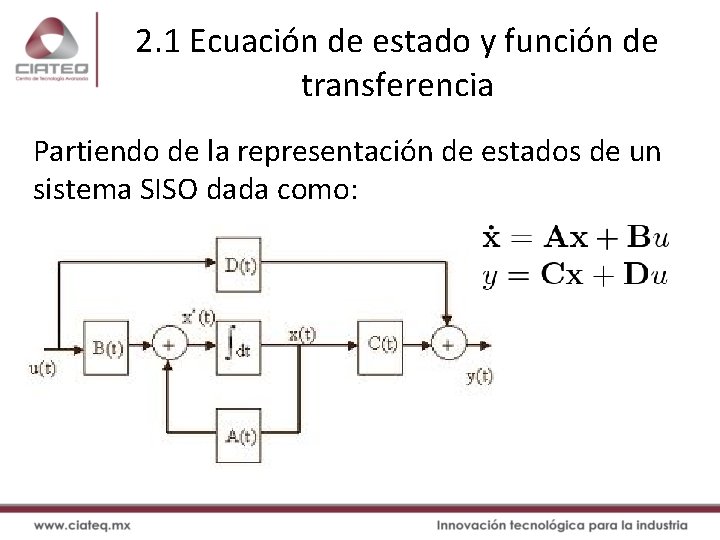
2. 1 Ecuación de estado y función de transferencia Partiendo de la representación de estados de un sistema SISO dada como:

2. 1 Ecuación de estado y función de transferencia Aplicando la transformada de Laplace, el sistema matricial se convierte en: en donde B es un matriz de orden nx 1 debido a que el sistema tiene una única entrada u. Ya que se esta buscando la función de transferencia de la ecuación de estados, se considera que las condiciones iníciales son cero.

2. 1 Ecuación de estado y función de transferencia Reordenando la ecuación de estados anterior se obtiene que: Asumiendo la invertibilidad de la matriz (s. I-A) de orden nxn, y denominando su inversa como φ(s), se tiene:

2. 1 Ecuación de estado y función de transferencia Sustituyendo ahora en la ecuación de salida se llega a: Por lo tanto la función de transferencia del sistema en estados es:

2. 1 Ecuación de estado y función de transferencia Puesto que: Queda claro que el polinomio denominador de la función de transferencia es det(s. I-A). Lo que significa que los polos del sistema son iguales a los valores propios de la matriz A, ya que se obtienen a partir de su ecuación característica.

2. 1 Ecuación de estado y función de transferencia En conclusión, los polos del sistema dependen sólo de la matriz A, mientras que los ceros dependen de las matrices A, B, C y D.

Ejercicio Obtenga la función de transferencia de:

2. 2 Descomposición Canónica Controlabilidad La ecuación x=Ax+Bu de estados es controlable si para cualquier x(0)=X 0 y cualquier X 1, existe u(t) que transfiere el estado de X 0 a X 1 en un tiempo finito.

2. 2 Descomposición Canónica Controlabilidad El rango de la matriz c es reconocido como el índice de controlabilidad

Ejemplo Calcule la matriz de controlabilidad y establezca si el sistema es estable:

Ejemplo Matriz de controlabilidad Det(c)≠ 0 Rango = Orden Índice de controlabilidad = 2 Sistema Controlable

Ejercicio Calcule la matriz de controlabilidad y establezca si el sistema es estable:

2. 2 Descomposición Canónica Observabilidad. 2011 Sistemas Lineales 17

2. 2 Descomposición Canónica Observabilidad. Se dice que el sistema es completamente observable si el estado x(t) se determina a partir de la medición de y(t) durante un intervalo de tiempo finito t 0 ≤ t 1. Por tanto el sistema es completamente observable si todas las transiciones de estado afectan eventualmente a todos los elementos del vector de salida. El concepto de observabilidad es útil al resolver el problema de reconstruir señales o variables de estado no medibles a partir de variables que si son medibles en un tiempo lo menor posible. En estas notas trataremos con sistemas lineales e invariantes en el tiempo; por lo que sin perder generalidad supondremos que t 0 es 0. 2011 Sistemas Lineales 18

2. 2 Descomposición Canónica Observabilidad. El concepto de observabilidad es muy importante porque, en el terreno práctico, la dificultad que se encuentra con el control mediante retroalimentación del estado es que algunas variables de estado no son asequibles para una medición directa , por lo que se hace necesario estimar las variables de estado no medibles para formar las señales de control. Más adelante se demostrará que tales estimaciones de las variables de estado son posibles si y sólo si el sistema es completamente observable. 2011 Sistemas Lineales 19

2. 2 Descomposición Canónica Observabilidad. 2011 Sistemas Lineales 20

2. 2 Descomposición Canónica Observabilidad. 2011 Sistemas Lineales 21

2. 2 Descomposición Canónica Observabilidad. Las condiciones para la observabilidad completa también se plantean en términos de las funciones de transferencia o las matrices de transferencia. La condición necesaria y suficiente para una observabilidad completa del estado es que no ocurra una cancelación en la función de transferencia o en la matriz de transferencia. Si ocurre una cancelación el modo cancelado no se puede observar en la salida. 2011 Sistemas Lineales 22

2. 2 Descomposición Canónica Observabilidad. Si un sistema es no observable de estado completo, pero su parte no observable es estable, entonces se dice que dicho sistema es solamente detectable. Un sistema observable de estado completo es siempre detectable. 2011 Sistemas Lineales 23

2. 2 Descomposición Canónica Observabilidad. 2011 Sistemas Lineales 24