SISMO www sismo srv br Signal Processing Research

SISMO www. sismo. srv. br Signal Processing Research, Training & Consulting www. sismo. srv. br Attribute-Assisted Seismic Processing and Interpretation http: //geology. ou. edu/aaspi/ Can we use the spectral ridges to estimate Q ? Marcílio Castro de Matos marcilio@matos. eng. br www. matos. eng. br 1

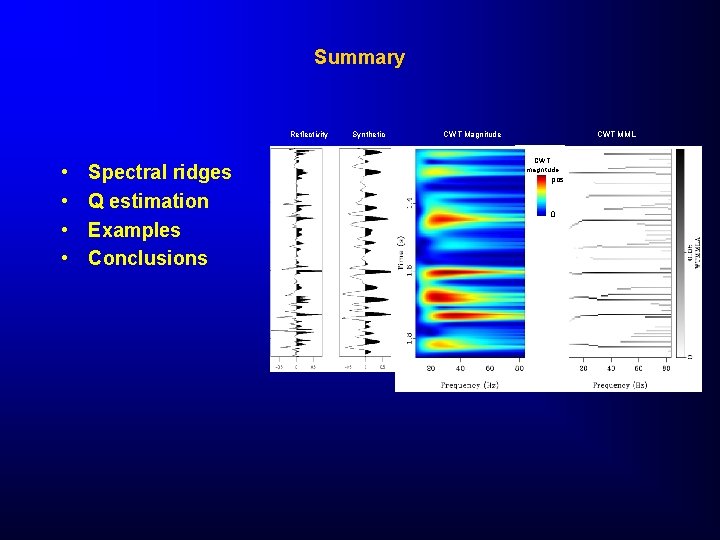
Summary Reflectivity • • Spectral ridges Q estimation Examples Conclusions Synthetic CWT Magnitude CWT MML CWT magnitude pos 0

Spectral ridges ü Introduction ü Continuous Wavelet Transform (very brief review) ü ICWTdec ü Examples ü Conclusions 3

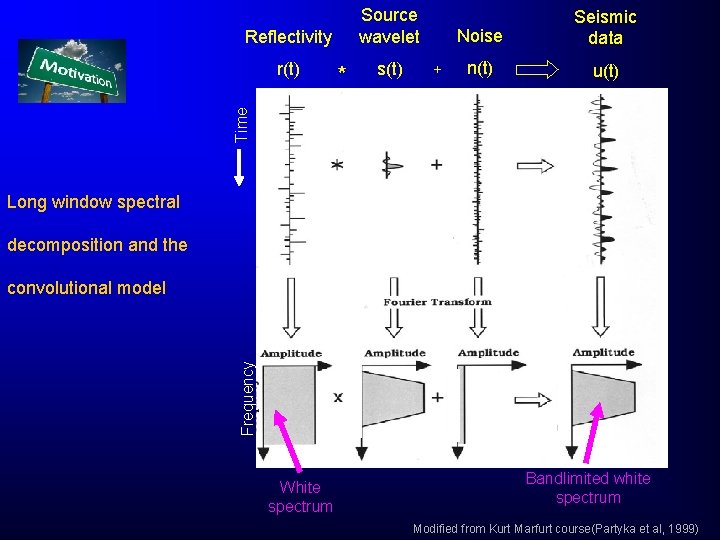
Source wavelet Reflectivity * s(t) + n(t) u(t) Time r(t) Noise Seismic data Long window spectral decomposition and the Frequency convolutional model White spectrum Bandlimited white spectrum Modified from Kurt Marfurt course(Partyka et al, 1999)

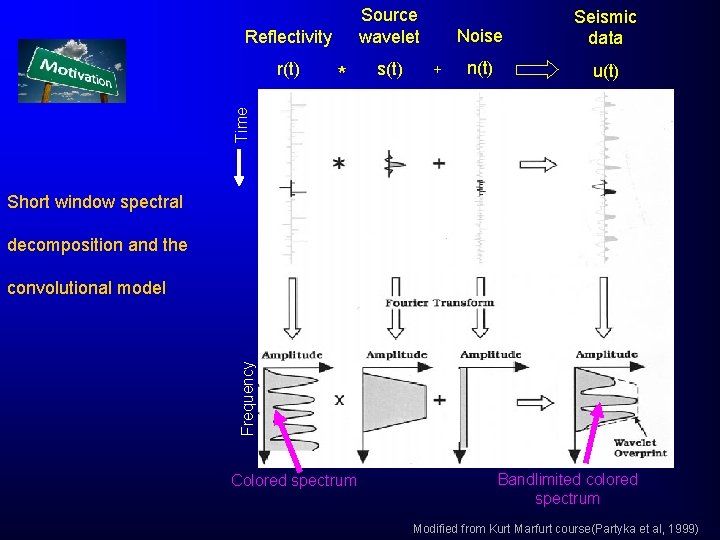
Source wavelet Reflectivity * s(t) + n(t) u(t) Time r(t) Noise Seismic data Short window spectral decomposition and the Frequency convolutional model Colored spectrum Bandlimited colored spectrum Modified from Kurt Marfurt course(Partyka et al, 1999)

1822 Fourier book From: http: //books. google. com/ Animated plot of the first five successive partial Fourier series. From wikipedia. org

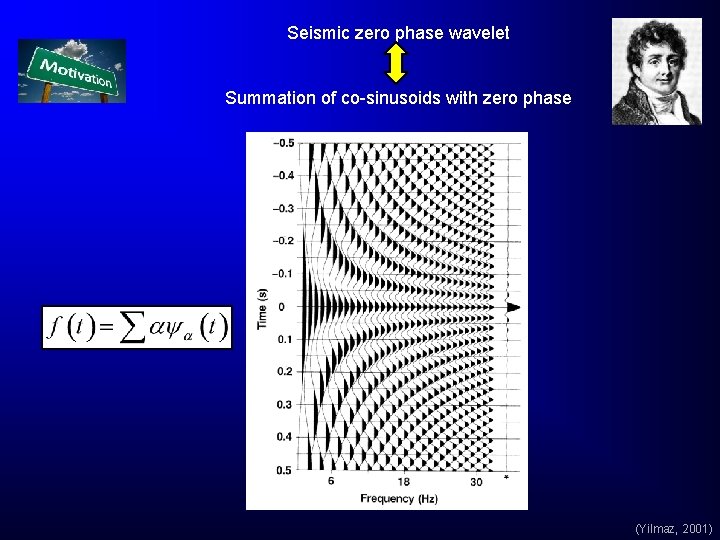
Seismic zero phase wavelet Summation of co-sinusoids with zero phase (Yilmaz, 2001)

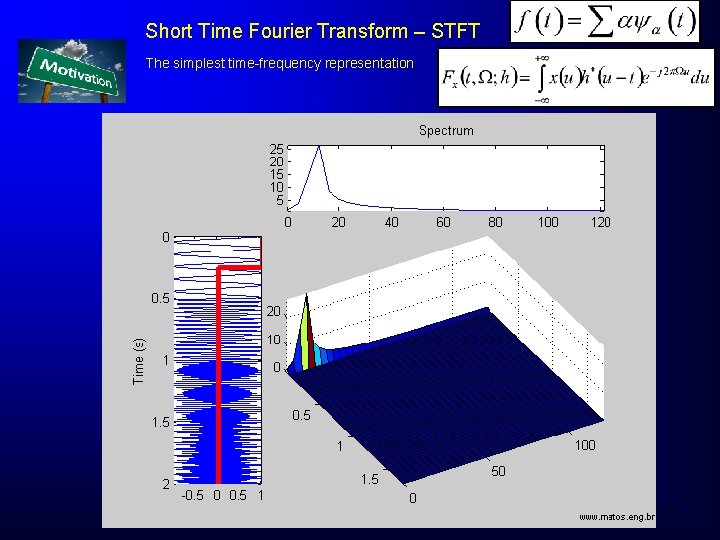
Short Time Fourier Transform – STFT The simplest time-frequency representation 8

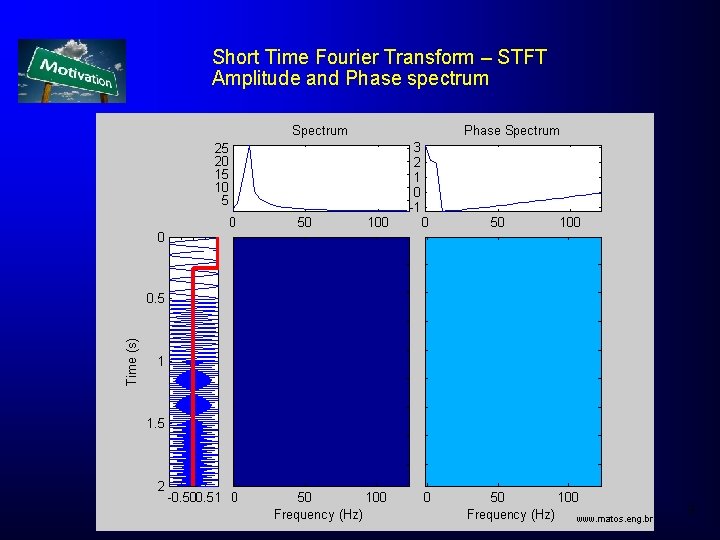
Short Time Fourier Transform – STFT Amplitude and Phase spectrum 9

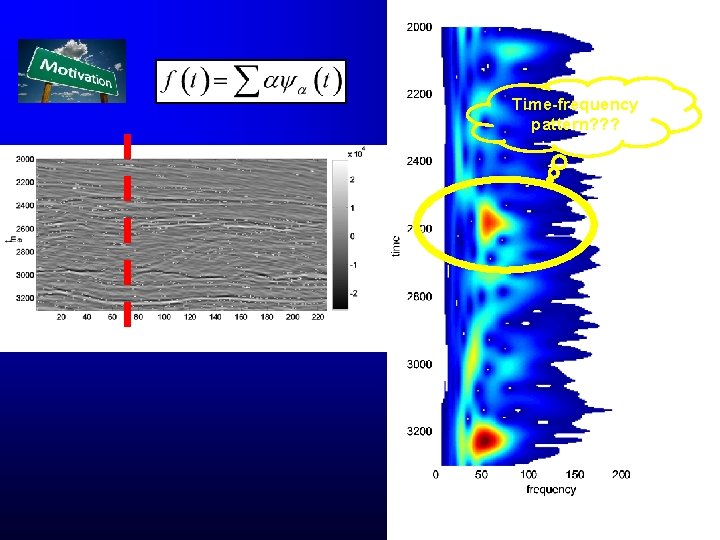
Time-frequency pattern? ? ?

Spectral ridges ü Introduction ü Continuous Wavelet Transform (very brief review) ü ICWTdec ü Examples ü Conclusions 11

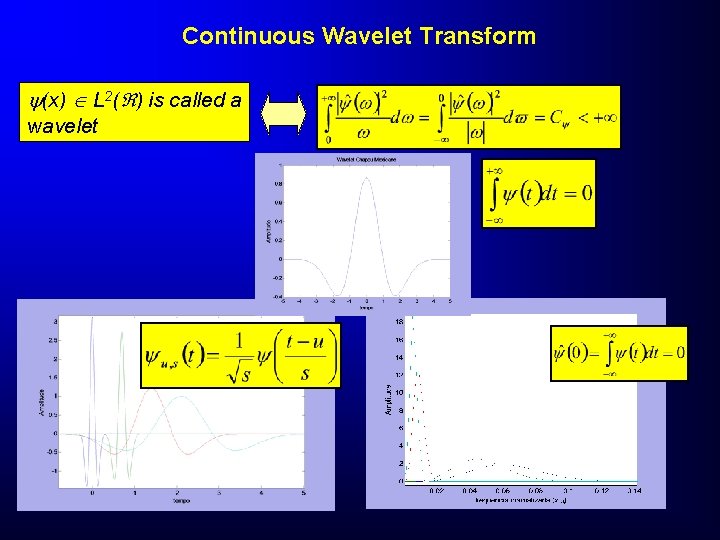
Continuous Wavelet Transform (x) L 2( ) is called a wavelet

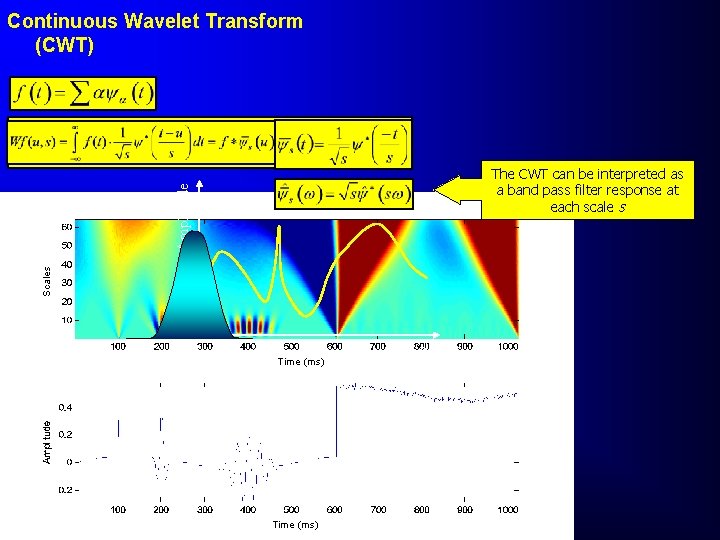
Continuous Wavelet Transform (CWT) Scales Amplitude The CWT can be interpreted as a band pass filter response at each scale s Time (ms) time

Grossmann and Morlet introduced CWT formally in 1984

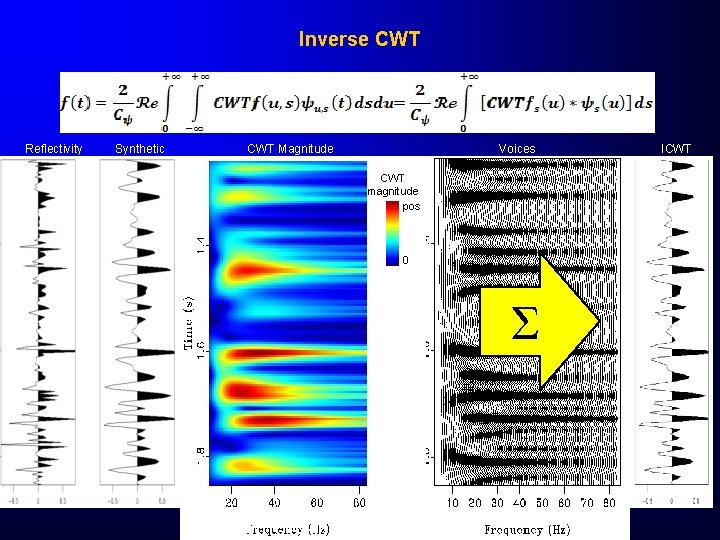
Inverse CWT Reflectivity Synthetic CWT Magnitude Voices CWT magnitude pos 0 Σ ICWT

Summary ü Introduction ü Continuous Wavelet Transform (very brief review) ü Pseudo deconvolution (icwtdec) ü Examples ü Conclusions 16

Math behind…

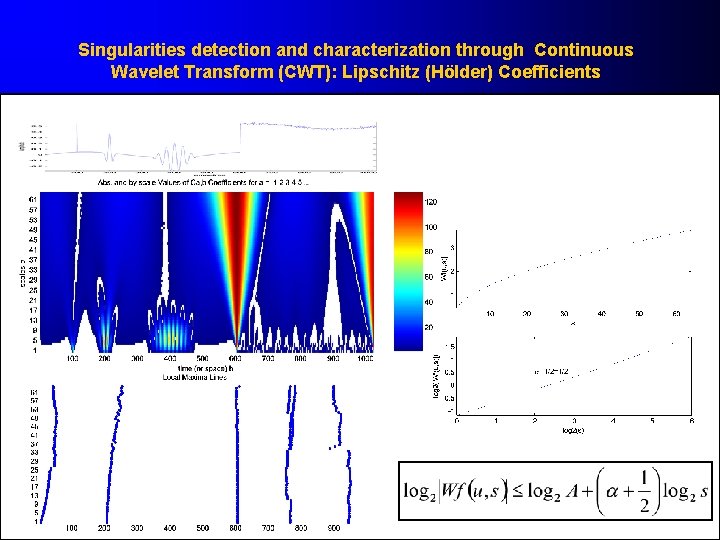
Singularities detection and characterization through Continuous Wavelet Transform (CWT): Lipschitz (Hölder) Coefficients

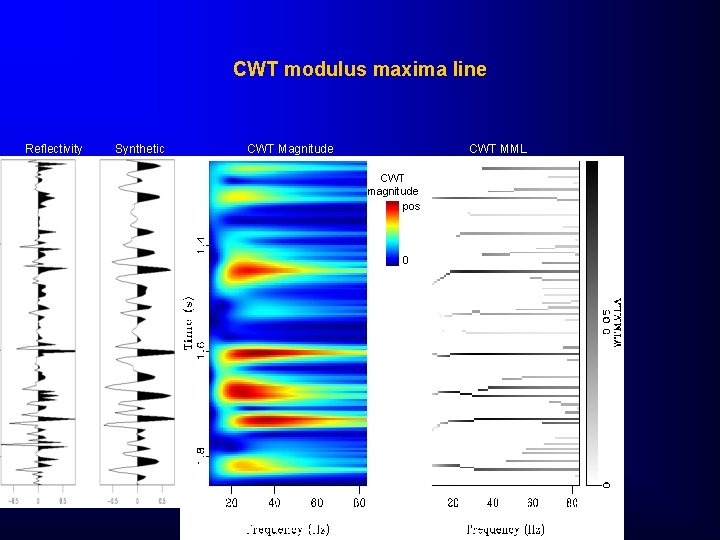
CWT modulus maxima line Reflectivity Synthetic CWT Magnitude CWT MML CWT magnitude pos 0

WTMMLA seismic applications

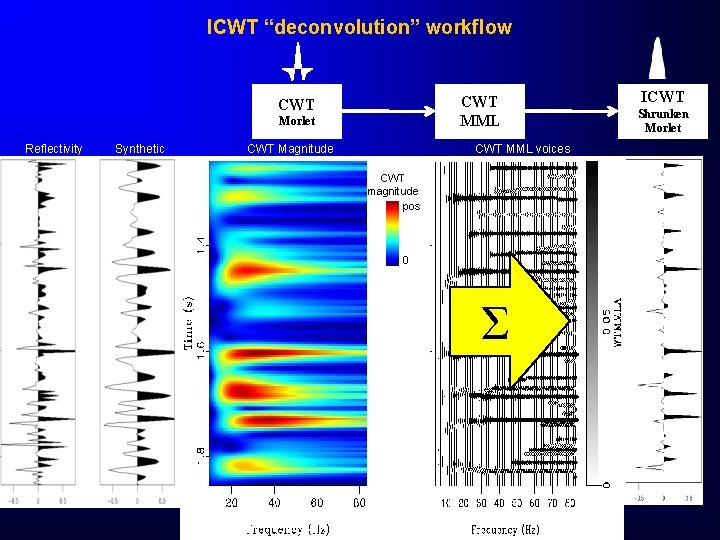
ICWT “deconvolution” workflow CWT MML CWT Morlet Reflectivity Synthetic CWT Magnitude CWT MML voices CWT magnitude pos 0 Σ ICWT Shrunken Morlet

Relative acoustic impedance from ICWTDEC WORKFLOW - Re-scale seismic trace: |s(t)|<<1 - Integration filter (Peacock, 1979) - High-pass filter

Summary ü Introduction ü Continuous Wavelet Transform (very brief review) ü ICWTdec ü Examples ü Conclusions 24

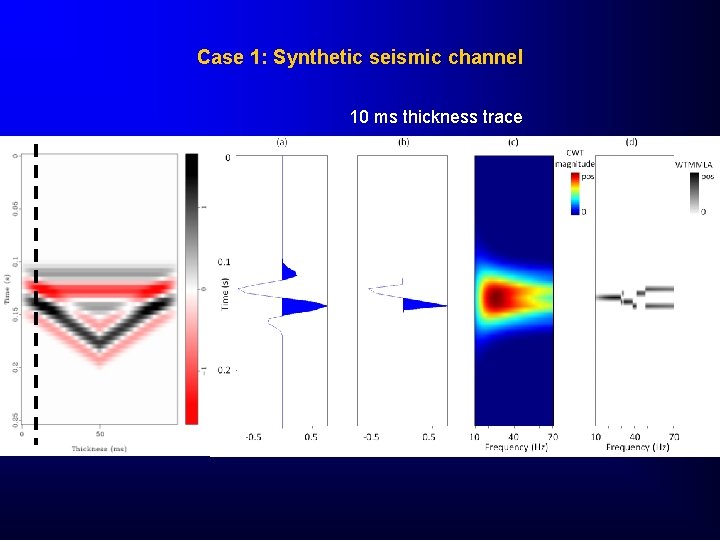
Case 1: Synthetic seismic channel 10 ms thickness trace

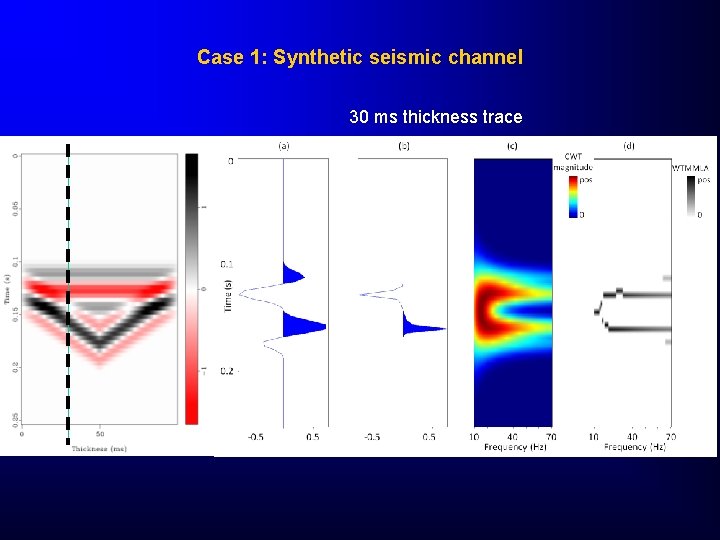
Case 1: Synthetic seismic channel 30 ms thickness trace

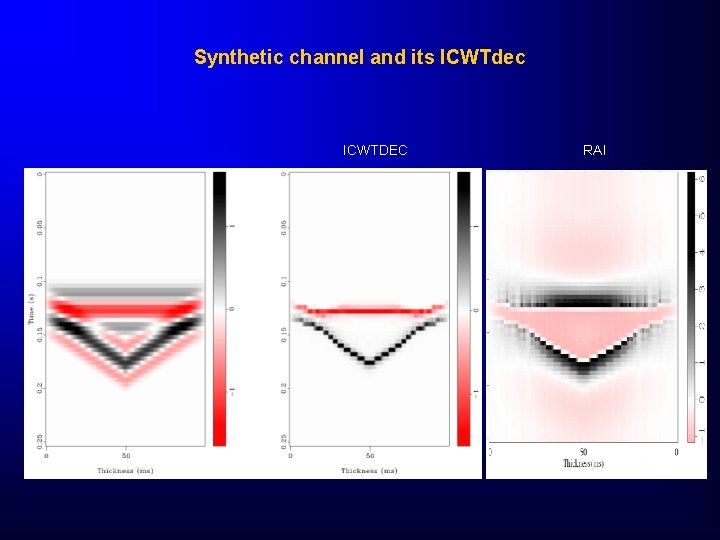
Synthetic channel and its ICWTdec ICWTDEC RAI

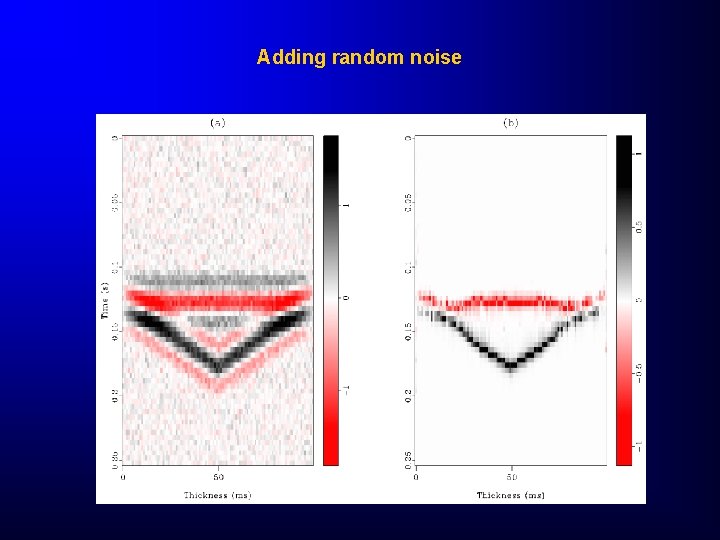
Adding random noise

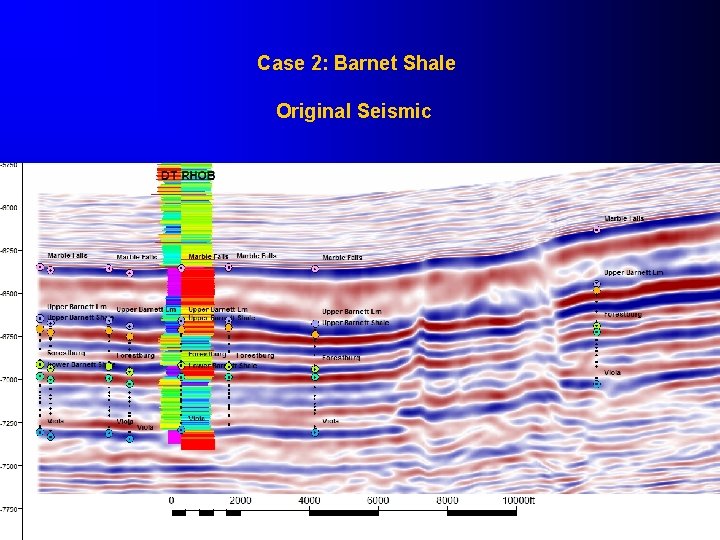
Case 2: Barnet Shale Original Seismic

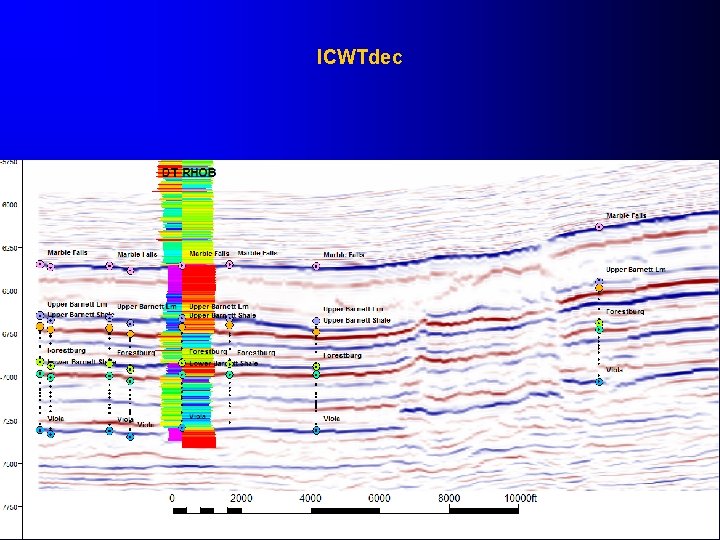
ICWTdec

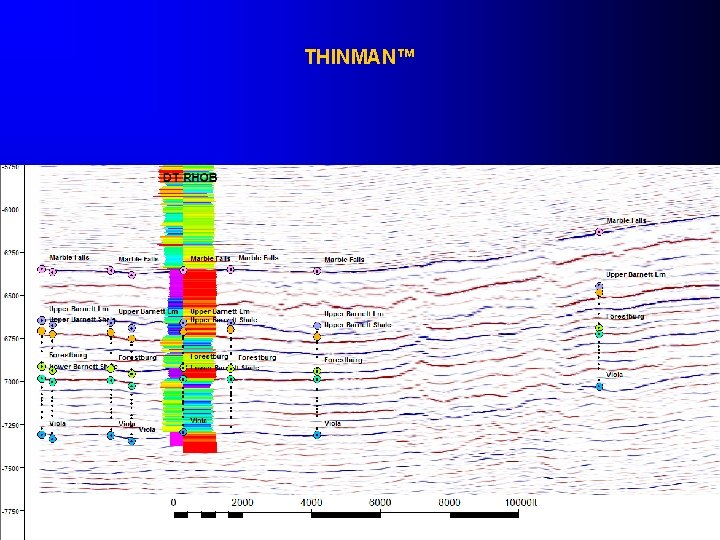
THINMAN™

Amplitude 60 Marble Falls 0 Upper Barnett Lm 60 Upper Barnett Sh Forestburg Lower Barnett Sh ICWTdec Viola

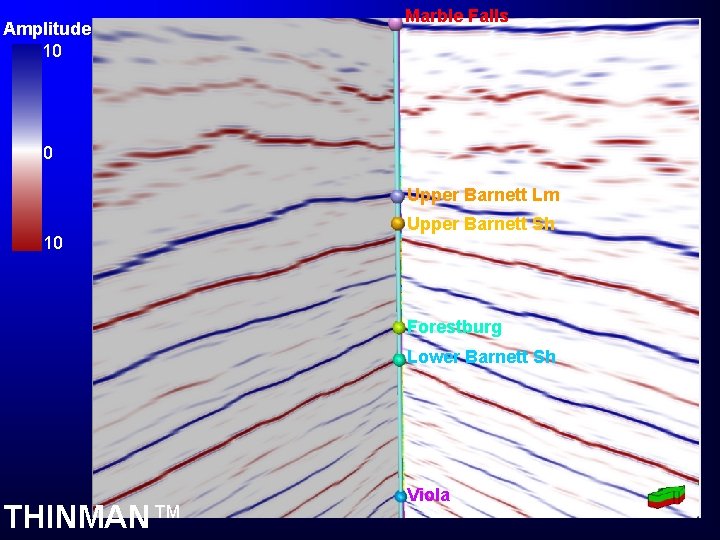
Amplitude 10 Marble Falls 0 Upper Barnett Lm 10 Upper Barnett Sh Forestburg Lower Barnett Sh THINMAN™ Viola

Case 3: Pre-stack (Hampson&Russel 2 D demo data set) Offset 0 0. 7 Twt (s)

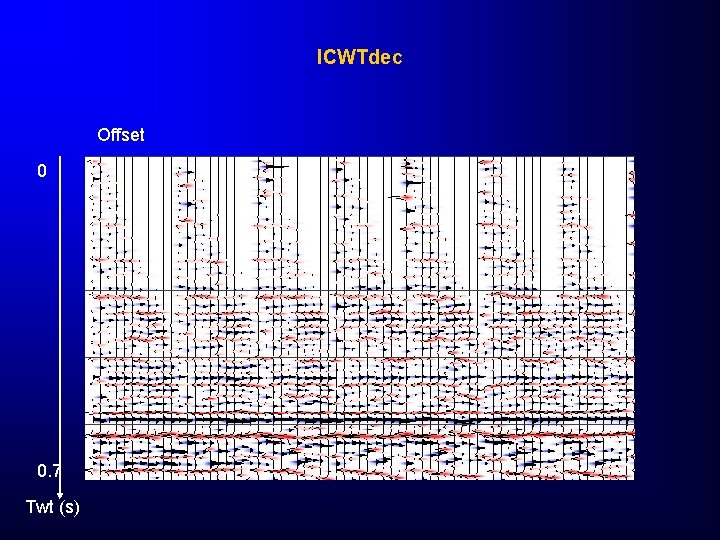
ICWTdec Offset 0 0. 7 Twt (s)

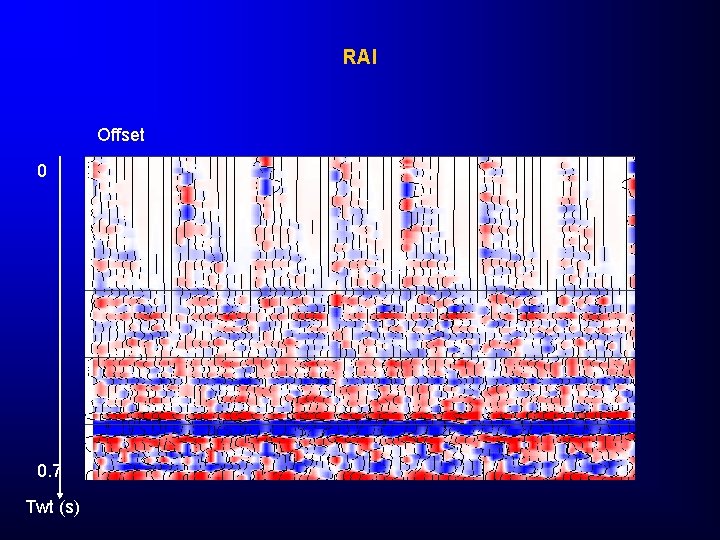
RAI Offset 0 0. 7 Twt (s)

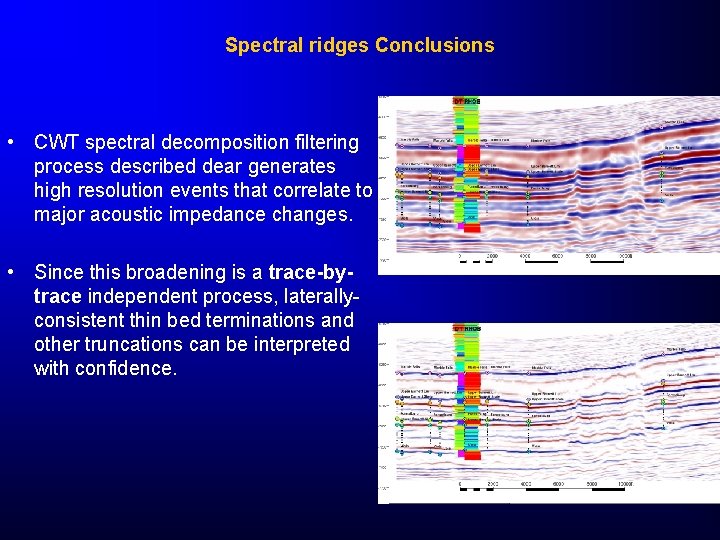
Spectral ridges Conclusions • CWT spectral decomposition filtering process described dear generates high resolution events that correlate to major acoustic impedance changes. • Since this broadening is a trace-bytrace independent process, laterallyconsistent thin bed terminations and other truncations can be interpreted with confidence.

Q estimation • Anelasticity and wave propagation “very brief” review • Q estimation and spectral ridges • Conclusions

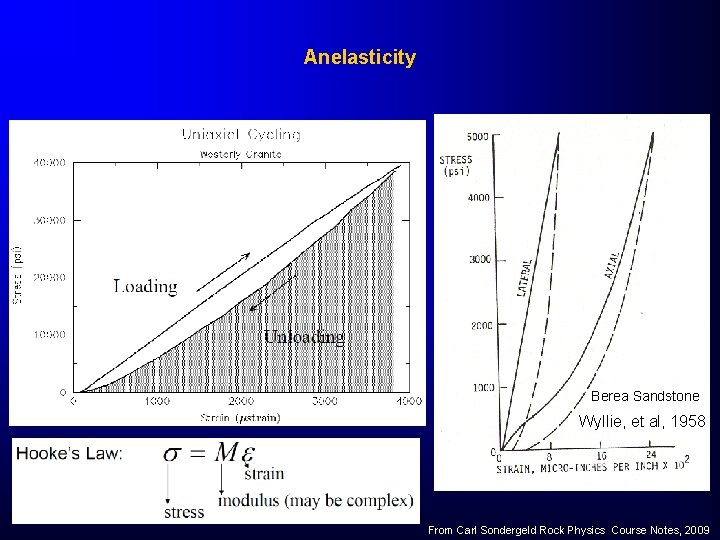
Anelasticity Berea Sandstone Wyllie, et al, 1958 From Carl Sondergeld Rock Physics Course Notes, 2009

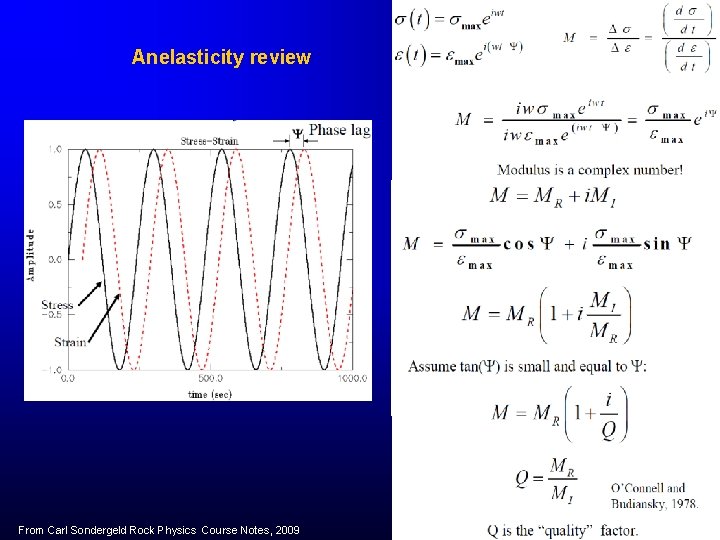
Anelasticity review From Carl Sondergeld Rock Physics Course Notes, 2009

Wave equation From Carl Sondergeld Rock Physics Course Notes, 2009

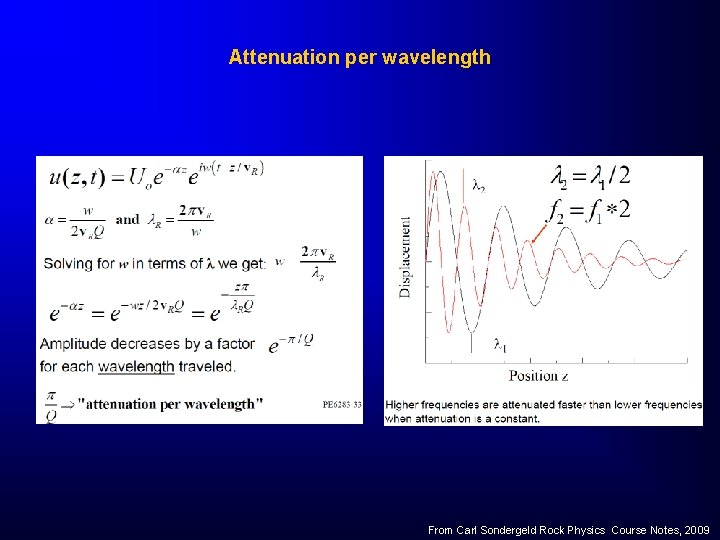
Attenuation per wavelength From Carl Sondergeld Rock Physics Course Notes, 2009

Normal incidence anelastic reflections From Carl Sondergeld Rock Physics Course Notes, 2009

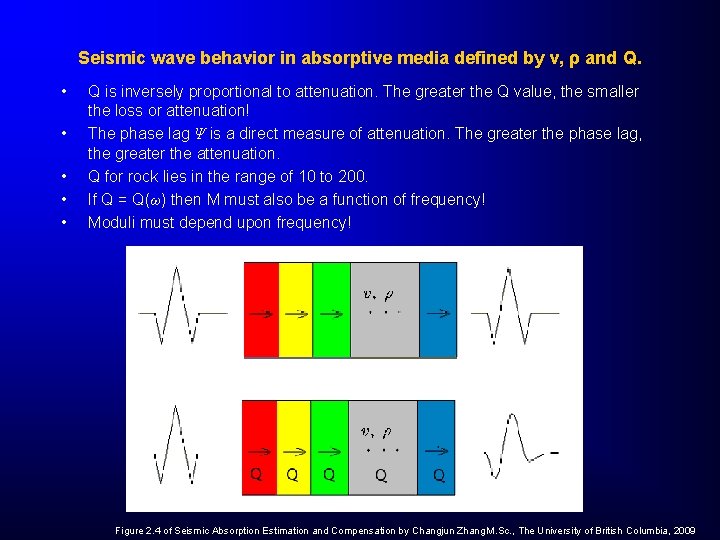
Seismic wave behavior in absorptive media defined by v, ρ and Q. • • • Q is inversely proportional to attenuation. The greater the Q value, the smaller the loss or attenuation! The phase lag Ψ is a direct measure of attenuation. The greater the phase lag, the greater the attenuation. Q for rock lies in the range of 10 to 200. If Q = Q(ω) then M must also be a function of frequency! Moduli must depend upon frequency! Figure 2. 4 of Seismic Absorption Estimation and Compensation by Changjun Zhang M. Sc. , The University of British Columbia, 2009

Q estimation • Anelasticity and wave propagation “very brief” review • Q estimation and spectral ridges • Conclusions

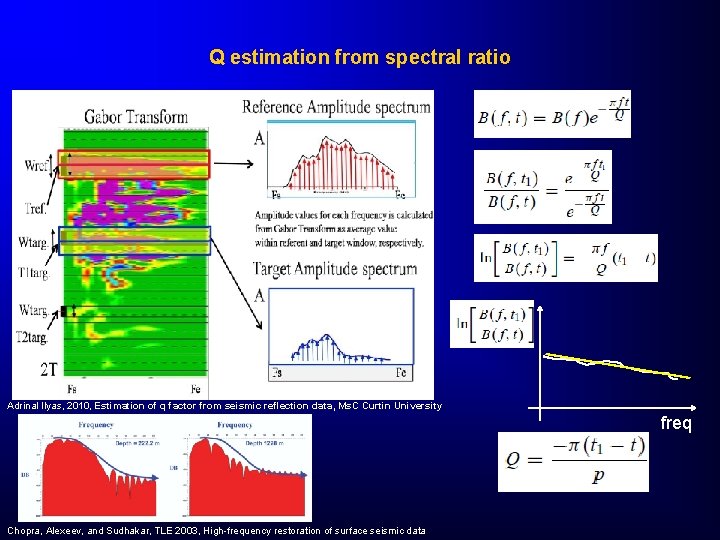
Q estimation from spectral ratio Adrinal Ilyas, 2010, Estimation of q factor from seismic reflection data, Ms. C Curtin University freq Chopra, Alexeev, and Sudhakar, TLE 2003, High-frequency restoration of surface seismic data

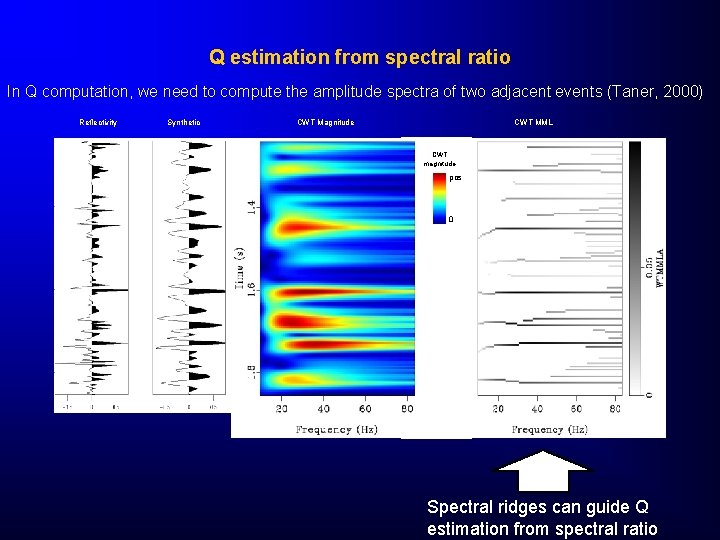
Q estimation from spectral ratio In Q computation, we need to compute the amplitude spectra of two adjacent events (Taner, 2000) Reflectivity Synthetic CWT Magnitude CWT MML CWT magnitude pos 0 Spectral ridges can guide Q estimation from spectral ratio

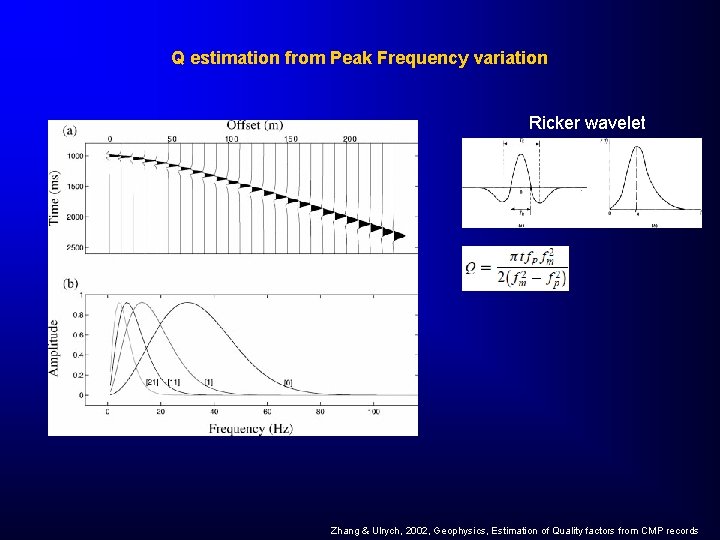
Q estimation from Peak Frequency variation Ricker wavelet Zhang & Ulrych, 2002, Geophysics, Estimation of Quality factors from CMP records

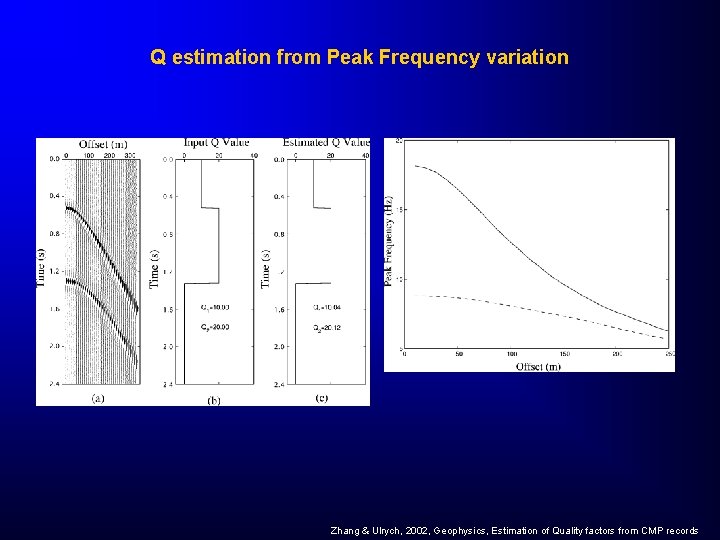
Q estimation from Peak Frequency variation Zhang & Ulrych, 2002, Geophysics, Estimation of Quality factors from CMP records

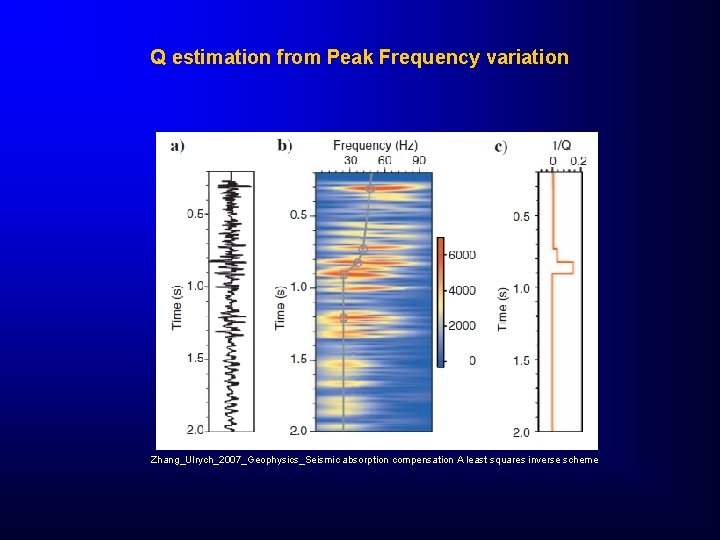
Q estimation from Peak Frequency variation Zhang_Ulrych_2007_Geophysics_Seismic absorption compensation A least squares inverse scheme

Frequency decay caused by thin-bed tuning and absorption Figure 4. 2 of Seismic Absorption Estimation and Compensation by Changjun Zhang M. Sc. , The University of British Columbia, 2009

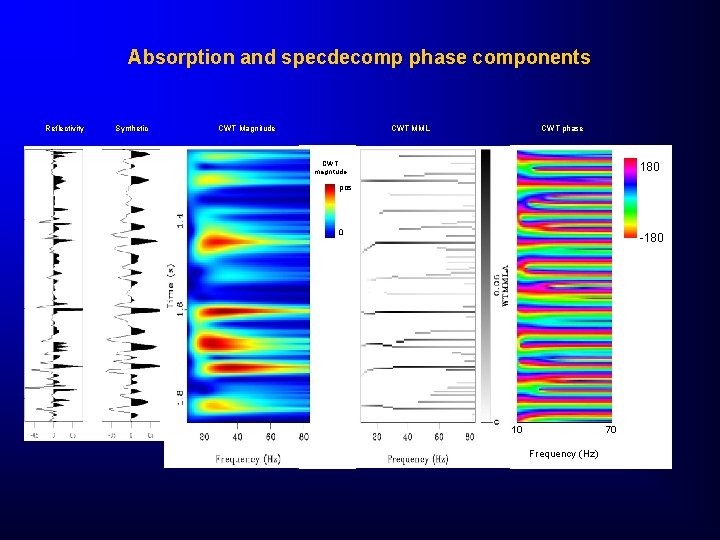
Absorption and specdecomp phase components Reflectivity Synthetic CWT Magnitude CWT phase CWT MML CWT magnitude 180 pos 0 -180 10 70 Frequency (Hz)

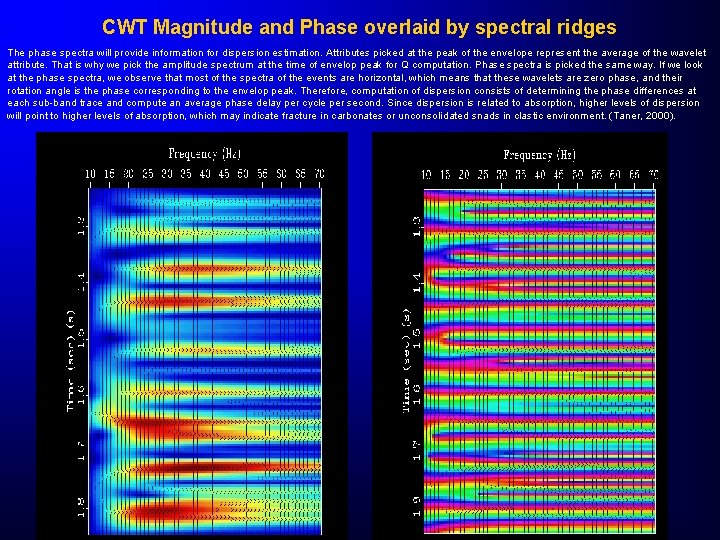
CWT Magnitude and Phase overlaid by spectral ridges The phase spectra will provide information for dispersion estimation. Attributes picked at the peak of the envelope represent the average of the wavelet attribute. That is why we pick the amplitude spectrum at the time of envelop peak for Q computation. Phase spectra is picked the same way. If we look at the phase spectra, we observe that most of the spectra of the events are horizontal, which means that these wavelets are zero phase, and their rotation angle is the phase corresponding to the envelop peak. Therefore, computation of dispersion consists of determining the phase differences at each sub-band trace and compute an average phase delay per cycle per second. Since dispersion is related to absorption, higher levels of dispersion will point to higher levels of absorption, which may indicate fracture in carbonates or unconsolidated snads in clastic environment. (Taner, 2000).

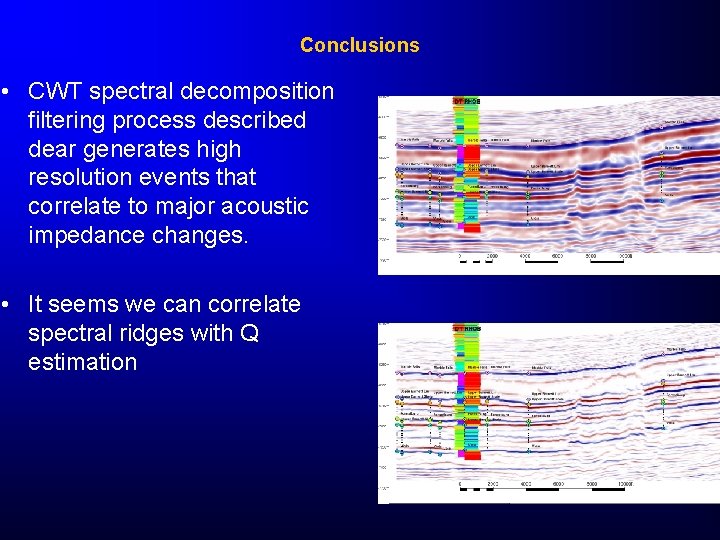
Conclusions • CWT spectral decomposition filtering process described dear generates high resolution events that correlate to major acoustic impedance changes. • It seems we can correlate spectral ridges with Q estimation

Acknowledgements Signal Processing Research, Training & Consulting www. sismo. srv. br Attribute-Assisted Seismic Processing and Interpretation http: //geology. ou. edu/aaspi/ Thanks to DEVON for providing a license to one of the seismic data volume used herein. Thanks to Carl Sondergeld Thanks to Roderick Perez from OU for his Barnet shale interpretation. Thanks also to PETROBRAS Reservoir Geophysics Management friends for their comments. Thank you for your attention!!! marcilio@matos. eng. br www. matos. eng. br