Selected Applications of Suffix Trees 1 Reminder suffix

Selected Applications of Suffix Trees 1

Reminder – suffix tree Suffix tree for string S of length m: • rooted directed tree with m leaves numbered 1, . . . , m. • each internal node, except the root, has at least 2 children. • each edge labeled with a nonempty substring of S. • edges out of a node begin with different characters. • path from the root to leaf i spells out suffix S[i. . . m]. 2

Reminder – suffix tree (continued) • Each substring a of S appears on some unique path from the root. • If a ends at point p, the leaves below p mark all its occurrences. a occurs in S starting at position j a is a prefix of S[j. . . m] a labels an initial part of the path from the root to leaf j. 3

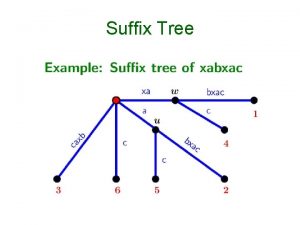
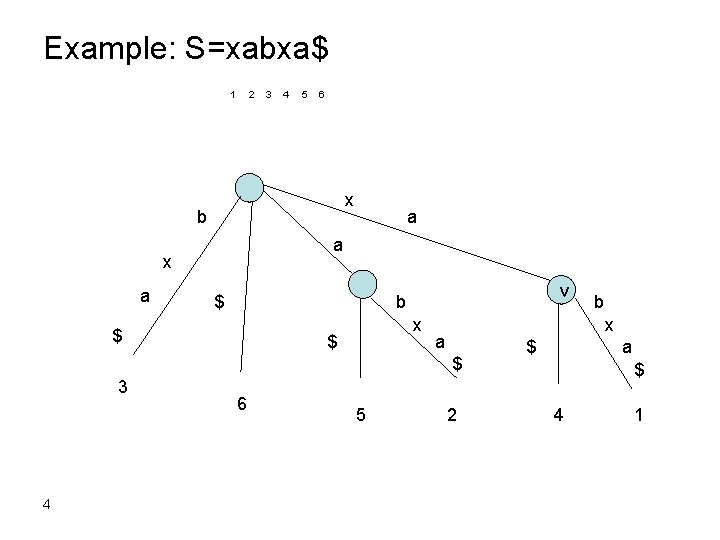
Example: S=xabxa$ 1 2 3 4 5 6 x b a x a a $ v b $ x a $ 3 4 6 5 b 2 $ a $ 4 1

Exact string matching Find all occurrences of pattern P in text T. • Build suffix tree for T O(m) (Ukkonen). • Match P along a path from the root O(1) per character (finite alphabet) O(n) total. • If P fully matches a path, then the leaves below mark all starting positions of P in T O(k) where k = number of occurrences. 5

Matching Statistics • ms(i) – the length of the longest substring of T starting at position i that matches a substring somewhere in P. • example: T = abcxabcdex, P = wyabcwzqabcdw ms(1)=3, ms(5)=4. • There is an occurrence of P starting at position i of T iff ms(i)=|P|. 6

Goal: Compute ms(i) for each position i in T, in O(m) total time, using only a suffix tree for P. • Naive way: match T[i. . . m] starting from the root. more than O(m) total. Using suffix links: • Build suffix tree for P (Ukkonen) and keep suffix links. • suffix link: pointer from internal node v with path-label xa to node s(v) with path-label a. (x character, a substring) 7

Compute ms(i) in order base case: For ms(1), match T[1. . . m] from the root. general case: Suppose the matching path for ms(i) ended at point b, then for ms(i+1): • Let v be the first internal node at or above b. • If there is no such v – search from the root. • Otherwise – follow the suffix link from v to s(v) and search from s(v). path_label(v)=xa is a prefix of T[i. . . m] path_label(s(v))=a is a prefix of T[i+1. . . m]. 8

skip / count • Let b denote the string between node v and point b. • substring xab in P matches a prefix of T[i. . . m]. • substring ab in P matches a prefix of T[i+1. . . m]. • Traverse the path labeled b out of s(v) using skip/count trick (time proportional to number of nodes on the path). • From the end of b, match single characters (starting with the first character that didn’t match for ms(i)). 9

Time analysis In the search for ms(i+1): • back up at most one edge from b to v O(1). • traverse suffix link from v to s(v) O(1). • traverse a b-path from s(v) in time proportional to the number of nodes on it O(m) total. • perform additional comparisons starting with the first character that didn’t match for ms(i) O(m) total. 10

Ziv-Lempel data compression 11

Definitions For any position i in string S of length m: • Priori - longest prefix of S[i. . . m] that occurs as a substring of S[1. . . i-1]. • li - length of Priori. • si - starting position of the left-most copy of Priori (li>0). Example: S = abaxcabaxabz, Prioir 7 = bax, l 7 = 3, s 7 = 2. • Copy of Priori starting at si is totally contained in S[1. . . i-1]. 12

Basic idea • Suppose the text S[1. . . i-1] has been represented (perhaps in compressed form) and li>0. • Then Priori need not be explicitly represented. • The pair (si, li) points to an earlier occurrence of Priori. • Example: S = abaxcabaxabz (2, 3) 13

Compression algorithm (outline) i : = 1 Repeat compute li and si if li > 0 then output (si, li) i : = i + li else output S(i) i : = i + 1 Until i > n 14

Examples S 1 = a a b a c b (1, 1) c a b a x (1, 3) x a b (1, 2) z z S 2 = ab ab abababab ab(1, 2)(1, 4) (1, 8) (1, 16) S = (ab)k compressed representation is O(log k) 15

Decompress • Process the compressed string left to right. • Any pair (si, li) in the representation points to a substring that has already been fully decompressed. 16

Computing (si, li) • The algorithm does not request (si, li) for any position i already in the compressed part of S. compute li and si if li > 0 then output (si, li) i : = i + li • For total O(m) time, find each requested pair (si, li) in O(li) time. 17

Implementation using suffix tree (1) Before compression: • Build a suffix tree T for S. • For each node v, compute cv : – the smallest leaf index in v’s subtree. – the starting position of the leftmost copy of the substring that labels the path from the root to v. • O(m) time. 18

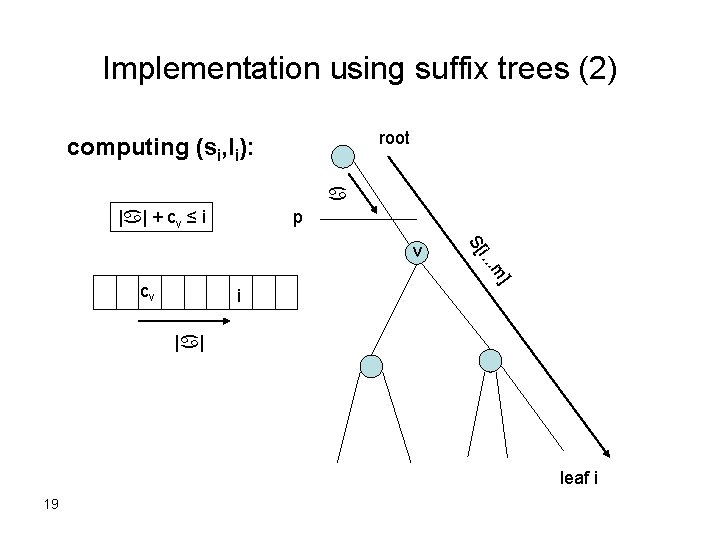
Implementation using suffix trees (2) root computing (si, li): a |a| + cv ≤ i p m i. . . S[ v ] cv i |a| leaf i 19

Implementation using suffix trees (3) • To compute (si, li), traverse the unique path in T that matches a prefix of S[i. . . m]: – Let: p - current point, v - first node at or below p. – Traverse as long as: string_depth(p) + cv ≤ i. – At the last point p of traversal: li = string_depth(p), si = cv. • O(li) time. 20

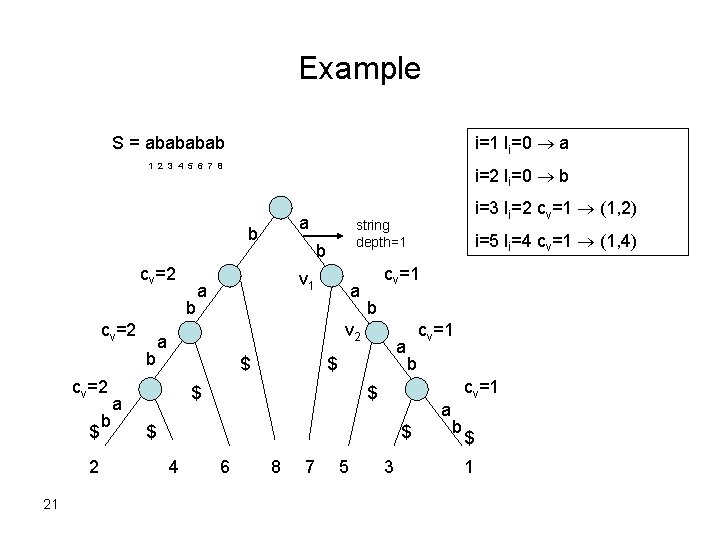
Example S = abab i=1 li=0 a 1 2 3 4 5 6 7 8 i=2 li=0 b a b cv=2 b b cv=2 $ 2 21 b v 1 a b a a $ $ i=5 li=4 cv=1 (1, 4) cv=1 v 2 a $ cv=2 string depth=1 b a i=3 li=2 cv=1 (1, 2) cv=1 b $ a $ $ 4 6 8 7 5 3 cv=1 b $ 1

Online version • Compress S as it is being input one character at a time. • Possible since S[1. . . i-1] is known before computing si, li. • Implementation: build suffix tree online. Ukkonen’s algorithm: – In phase i, build implicit suffix tree Ti for prefix S[1. . . i]. 22

Claim 1 Assume: – The compaction has been done for S[1. . . i-1]. – Implicit suffix tree Ti-1 for S[1. . . i-1] has been built. – cv values are given for each node v in Ti-1. Then (si, li) can be obtained in O(li) time. 23

Suppose we had a suffix tree for S[1. . . i-1] with cv values We could find (si, li) in O(li) time. li = string_depth(p) root si = cv S(i) S(i+1). . . p S(k-1) c S(k) v 24

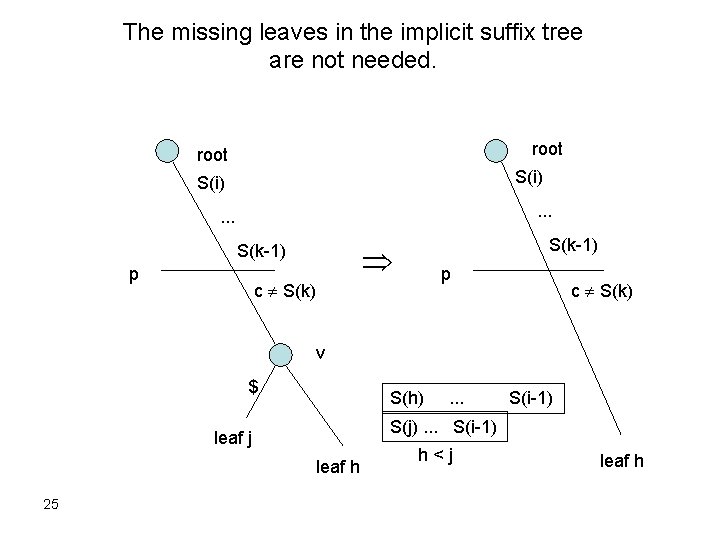
The missing leaves in the implicit suffix tree are not needed. root S(i) . . . p S(k-1) p c S(k) v $ S(h) S(i-1) S(j). . . S(i-1) leaf j leaf h 25 . . . h<j leaf h

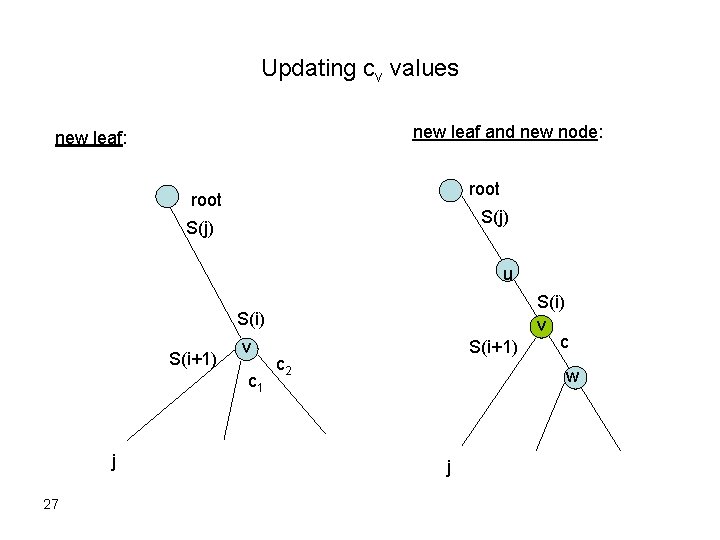
Claim 2 cv values for all implicit suffix trees can be computed in total O(m) time. • In Ukkonen’s algorithm: – Only extension rule 2 updates cv values. – Whenever a new internal node v is created by splitting an edge (u, w): cv cw. – Whenever a new leaf j is created: cj j. constant update time per new node. 26

Updating cv values new leaf and new node: new leaf: root S(j) u S(i) S(i+1) v c 1 j 27 S(i+1) c 2 S(i) v c w j

Online algorithm • Base case: output S(1) and build T 1. • General case: Suppose S[1. . . i-1] has been compressed and Ti-1 with cv values has been constructed. – – – Match S(i), S(i+1), . . . along a path from the root in Ti-1. Let S(k) be the first that doesn’t match. Find (si, li). If li = 0, output S(i) and build Ti with cv. If li > 0, output (si, li) and build Ti, . . . , Tk-1 with cv. • Total time: O(m). 28

Maximal Repetitive Structures 29

Maximal Pair • A maximal pair in string S: A pair of identical substrings a and b in S s. t. the character to the immediate left (right) of a is different from the character to the immediate left (right) of b. • Extending a and b in either direction would destroy the equality of the two strings. • Example: S = xabcyiiizabcqabcyrxar 30

Maximal Pair (continued) • Overlap is allowed: S = cxxaxxaxxb cxxaxxaxxb • To allow a prefix or suffix of S to be part of a maximal pair: S #S$ (#, $ don’t appear in S). Example: #abcxabc$ 31

Maximal Repeat • A maximal repeat in string S: A substring of S that occurs in a maximal pair in S. • Example: S = xabcyiiizabcqabcyrxar maximal repeats: abc, abcy, . . . 32

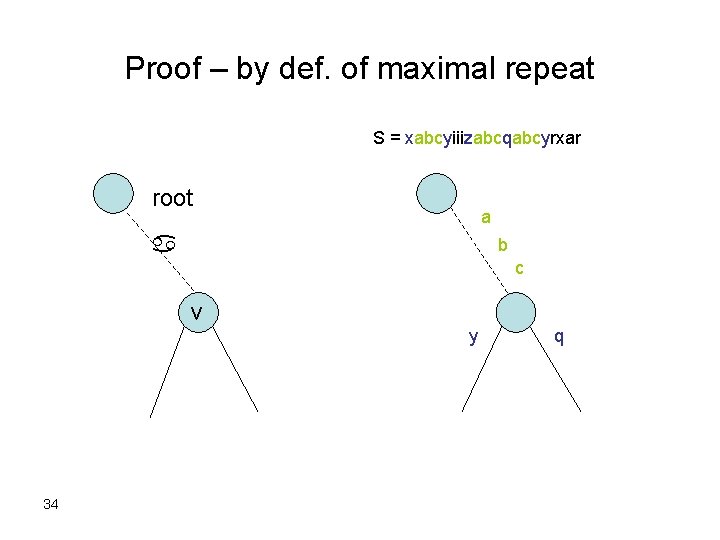
Finding All Maximal Repeats In Linear Time • Given: String S of length n. • Goal: Find all maximal repeats in O(n) time. • Lemma: Let T be a suffix tree for S. If string a is a maximal repeat in S, then a is the path-label of an internal node v in T. 33

Proof – by def. of maximal repeat S = xabcyiiizabcqabcyrxar root a a b c v y 34 q

Conclusion • There can be at most n maximal repeats in any string of length n. • Proof: by the lemma, since T has at most n internal nodes. 35

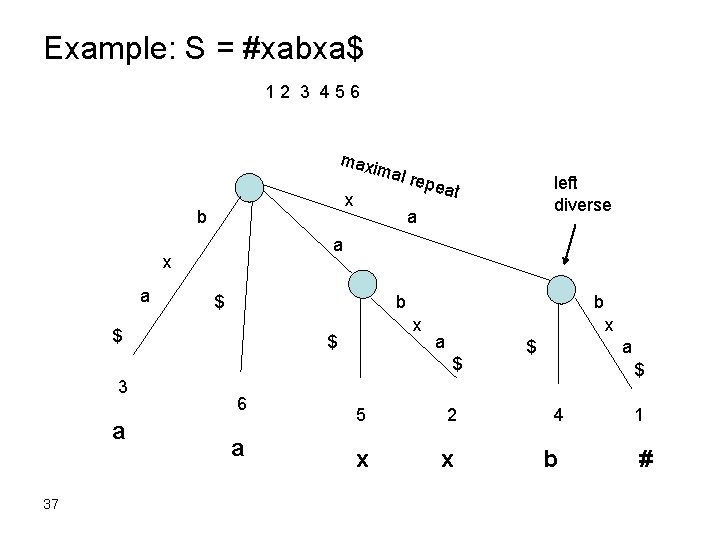
Which internal nodes correspond to maximal repeats? • The left character of leaf i in T is S(i-1). • Node v of T is left diverse if at least 2 leaves in v’s subtree have different left characters. • A leaf can’t be left diverse. • Left diversity propagates upward. 36

Example: S = #xabxa$ 12 3 456 max imal x b a $ b x $ x a $ 3 a 37 left diverse at a x a repe 6 a 5 2 x x $ a $ 4 b 1 #

Theorem The string a labeling the path to an internal node v of T is a maximal repeat v is left diverse. 38

Proof of • Suppose a is a maximal repeat • It participates in a maximal pair • It has at least two occurrences with distinct left characters: xa, ya, x y • Let i and j be the two starting positions of a. Then leaves i and j are in v’s subtree and have different left characters x, y. • v is left diverse. 39

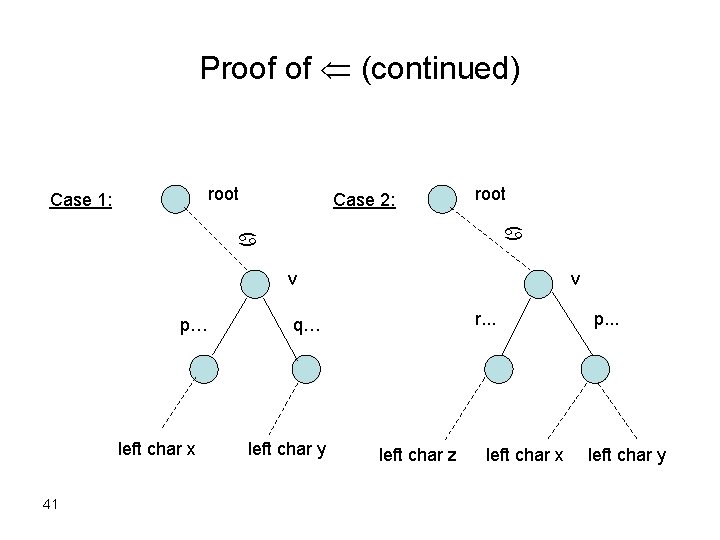
Proof of • Suppose v is left diverse there are substrings xap and yaq in S, x y. • If p q a’s occurrences in xap and yaq form a maximal pair a is a maximal repeat. • If p=q since v is a branching node, there is a substring zar in S, r p. If z x It forms a maximal pair with xap. If z y It forms a maximal pair with yap. In either case, a is a maximal repeat. 40

Proof of (continued) root Case 1: Case 2: root a a v p… left char x 41 v r. . . q… left char y left char z left char x p. . . left char y

Compact Representation • Node v in T is a frontier node if: – v is left diverse. – none of v’s children are left diverse. • Each node at or above the frontier is left diverse. • The subtree of T from the root down to the frontier nodes is a compact representation of the set of all maximal repeats of S. • Representation in O(n) though total length may be larger. 42

Linear time algorithm • Build suffix tree T. • Find all left diverse nodes in linear time. • Delete all nodes that aren’t left diverse, to achieve compact representation: 43

finding all left diverse nodes in linear time • Traverse T bottom-up, recording for each node: – either that it is left diverse – or the left character common to all leaves in its subtree. • For each leaf: record its left character. • For each internal node v: – If any child is left diverse v is left diverse. – Else If all children have a common character x record x for v. – Else record that v is left diverse. 44

Finding All Maximal Pairs In Linear Time • Not every two occurrences of a maximal repeat form a maximal pair. Example: S = xabcyiiizabcqabcyrxar • There can be more than O(n) maximal pairs. • The algorithm is O(n+k) where k is the number of maximal pairs. 45

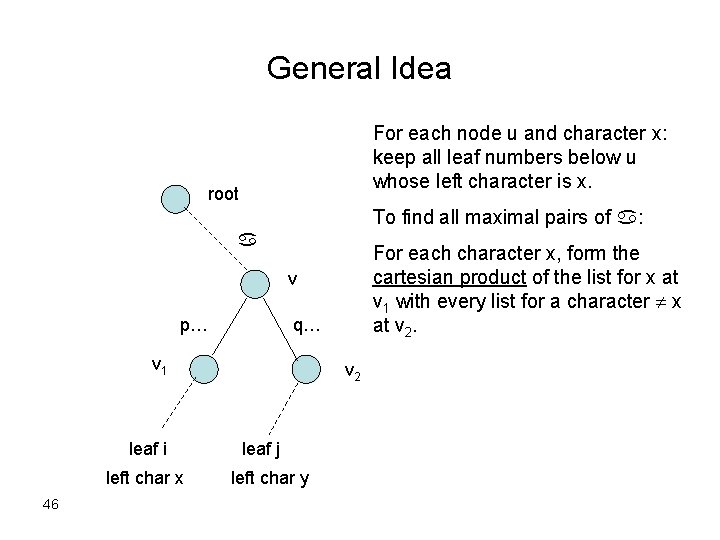
General Idea For each node u and character x: keep all leaf numbers below u whose left character is x. root To find all maximal pairs of a: a For each character x, form the cartesian product of the list for x at v 1 with every list for a character x at v 2. v p… q… v 1 leaf i left char x 46 v 2 leaf j left char y

The Algorithm • Build suffix tree T for S. • Record the left character of each leaf. • Traverse T bottom-up. • At each node v with path-label a: – Output all maximal pairs of a: cartesian product of lists (u, x) and (u’, x’) for each pair of children u u’ and pair of characters x x’. – Create the lists for node v by linking the lists of v’s children. 47

Time Analysis • Suffix tree construction O(n). • Bottom-up traversal including all list-linking O(n). • All cartesian product operations O(k), where k is the number of maximal pairs. • Total O(n+k). 48

Finding All Supermaximal Repeats In Linear Time • supermaximal repeat: a maximal repeat that isn’t a substring of any other maximal repeat. • Example: S = xabcyiiizabcqabcyrxar abcy is supermaximal, abc isn’t. • Theorem: A left diverse internal node v in the suffix tree for S represents a supermaximal repeat iff – all of v’s children are leaves – and each has a distinct left character 49

Longest Common Extension 50

Longest common extension problem Preprocess strings S 1 and S 2 s. t. the following queries can be computed in O(1) time each: • Given index pair (i, j), find the length of the longest substring of S 1 starting at position i that matches a substring of S 2 starting at position j. S 1: . . . abcdzzz. . . S 2: . . . abcdefg. . . j 51 i

Solution Preprocess: O(|S 1|+|S 2|) • Build generalized suffix tree T for S 1 and S 2. • Preprocess T for constant-time LCA queries. • Compute string-depth of every node. To answer query (i, j): O(1) • Find LCA node v of leaves corresponding to suffix i of S 1 and suffix j of S 2. • Return string-depth(v). 52

Tandem Repeats 53

Definition tandem repeat: a string a that can be written as a = bb, where b is a substring. s=xababy a b|a b b = ab a b|a b b a|b a b = ba b a|b a b = abab a b|a b note: b is not required to be of maximal length. 54

Finding all tandem repeats – simple solution For each feasible pair of start position i and middle position j: • Perform a longest common extension query from i and j. • If the extension from i reaches j or beyond, (i, j) defines a tandem repeat. 1. . . i. . . j-1 j. . . 2 j-i-1 2 j-i. . . n j-i 55 j-i

Time analysis • Preprocess for longest common extension: O(n). • O(n 2) feasible pairs, O(1) time to check each one. • O(n 2) total. 56

Finding all tandem repeats – faster solution • Due to Landau & Schmidt. • O(nlogn + z) time. • z = total number of tandem repeats in S. • z can be as large as Ө(n 2). • Example: all n characters are the same. • In practice, z is expected to be smaller. 57

Divide and conquer Let h = n/2. • Find all tandem repeats contained entirely in the first half of S (up to h). • Find all tandem repeats contained entirely in the second half of S (after h). • Find all tandem repeats where the first copy contains h. • Find all tandem repeats where the second copy contains h. 58

Solution of subproblems • 1 and 2 solved recursively. • 3 and 4 symmetric to each other. • Remains to show: solution for 3. 59

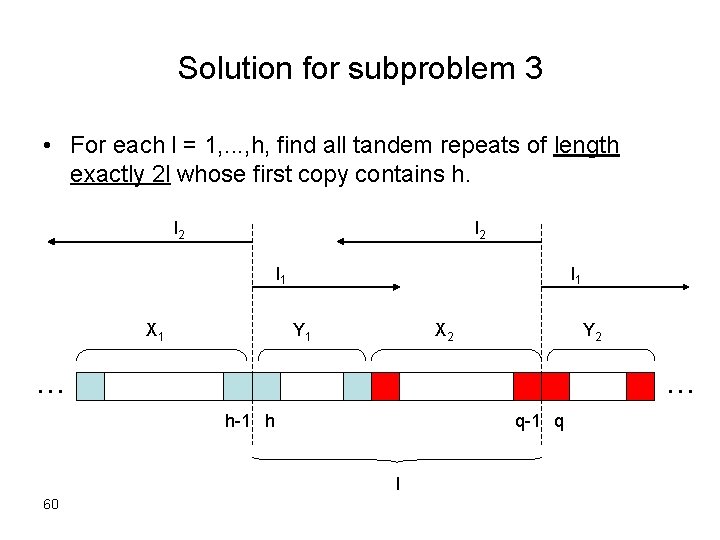
Solution for subproblem 3 • For each l = 1, . . . , h, find all tandem repeats of length exactly 2 l whose first copy contains h. l 2 l 1 X 1 l 1 Y 1 X 2 Y 2 . . . h-1 h q-1 q l 60

Algorithm for fixed l 1. Let q = h+l. 2. Compute longest common extension from h and q. Let l 1 denote its length. 3. Compute longest common extension from h-1 and q-1 in reverse direction. Let l 2 denote its length. 4. There is a tandem repeat of length 2 l whose first copy contains h iff l 1 1 and l 1 + l 2 l. 61

Output for fixed l 5. If the condition holds, output starting positions: Max(h-l 2 , h-l+1), . . . , Min(h+l 1 -l , h). l 1 l 2 h-l 2 h+l 1 -l h -l 62 h+l-l 2 h+l 1 q

Time analysis • For fixed l: – O(1) longest common extension queries. • For subproblem 3 on a string of length n: – O(n) longest common extension queries. • Entire algorithm on a string of length n: – Let T(n) denote the number of longest common extension queries for a string of length n. T(n) = 2 T(n/2) + 2 n T(n) = O(nlogn) – Including output: O(nlogn + z) total. 63

Inexact Matching 64

The k-mismatch problem • Given: pattern P, text T, fixed number k. • k-mismatch of P: a |P|-length substring of T that matches at least |P|-k characters of P (i. e. it matches P with at most k mismatches). • The k-mismatch problem: Find all k-mismatches of P in T. 65

Example P = bend T = abentbananaend k=2 T contains three 2 -mismatches of P: aben tbananaend bend 1 -mismatch 2 -mismatch 66 1 -mismatch

Solution • Notation: |P|=n, |T|=m, k independent of n and m (k<<n). • General idea: – For each position i in T, determine whether a k-mismatch of P begins at position i. – To do this efficiently: successively execute up to k+1 longest common extension queries. – A k-mismatch of P begins at position i iff these extensions reach the end of P. 67

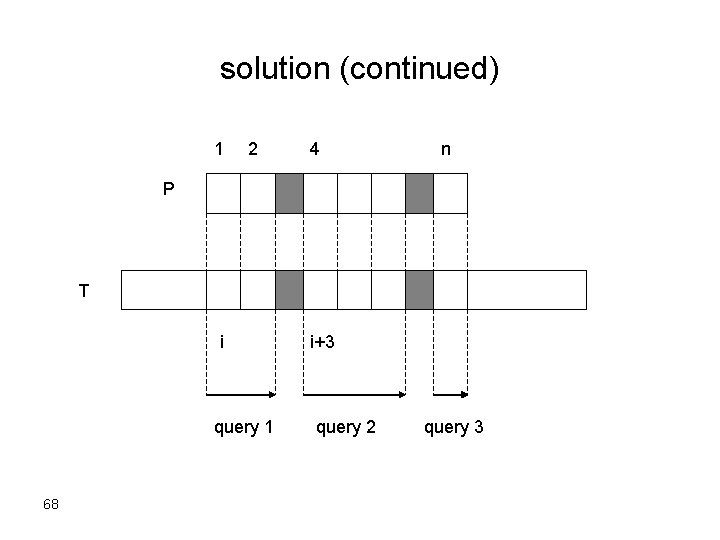
solution (continued) 1 2 4 n P T i query 1 68 i+3 query 2 query 3

Algorithm for index i 1. 2. 3. 4. 69 j 1 i’ i count 0 Compute the length l of the longest common extension starting at positions j of P and i’ of T. if j+l=n+1 then a k-mismatch of P occurs in T starting at i; stop. if count<k then count+1 j j+l+1 i’ i’+l+1 go to step 2. else, a k-mismatch of P does not occur in T starting at i; stop.

Time Analysis • Preprocessing of T and P for longest common extension queries O(m). • For each index i=1, . . . , m-n+1 of T, up to k+1 longest common extension queries O(k) per index O(km) total. • Total O(km) time. 70

k-mismatch tandem repeat • definition: tandem repeat in which the two copies differ by at most k mismatches. • example: axab|aybb • goal: find all k-mismatch tandem repeats. • simple solution: For each feasible pair of starting position i and middle position j, check if S[i. . . j-1] and S[j. . . 2 j-i-1] match with at most k mismatches. O(kn 2) • 71 faster solution exists: O(knlog(n/k)+z).

faster k-mismatch tandem repeats • O(knlog(n/k)+z) • same divide and conquer algorithm. • subproblem 3 for fixed l: find all k-mismatch tandem repeats of length 2 l whose first copy contains h. • let q = h+l. • run k successive longest common extension queries forward from h and q. mark every mismatch with ->. • run k successive longest common extension queries backward from h-1 and q-1. mark every mismatch with < • position t in [h+1, q] is a middle position of a k-mismatch tandem repeat iff the number of -> mismatches in positions h, . . . , t-1 plus the number of <- mismatches in positions t, . . . , q-1 is ≤ k. 72

faster k-mismatch tandem (continued) • accee|abcde|accdd h t q • calculate sums only for positions with arrows, to get intervals of legal midpoints. • O(k) time per fixed l, and any l ≤ k need not be checked. 73