MEASURES OF DISPERSION MEASURES OF DISPERSION The measures

MEASURES OF DISPERSION

MEASURES OF DISPERSION The measures of central tendency, such as the mean, median and mode, do not reveal the whole picture of the distribution of a data set. Two data sets with the same mean may have completely different spreads. The variation among the values of observations for one data set may be much larger or smaller than for the other data set. NOTE: the words dispersion, spread and variation have the same meaning.

MEASURES OF DISPERSION: example Consider the following two data sets on the ages of all workers in each of two small companies. Company 1: 47 Company 2: 38 35 40 36 45 70 33 18 52 27 39 The mean age of workers in both these companies is the same: 40 years. By knowing only these means, we may deduce that the workers have a similar age distribution in the two companies. But, the variation in the workers’ age is very different for each of these two companies. Company 1 36 35 27 38 40 45 47 It has a much larger variation than ages of the workers in the first company Company 2 18 39 33 52 70

MEASURES OF DISPERSION The mean, median or mode is usually not by itself a sufficient measure to reveal the shape of a distribution of a data set. We also need a measure that can provide some information about the variation among data set values. The measures that help us to know about the spread of a data set are called measures of dispersion. The measures of central tendency and dispersion taken together give a better picture of a data set. We consider 3 measures of dispersion: 1. Range 2. Variance 3. Standard Deviation

RANGE Definition the range is the simplest measure of dispersion and it is obtained by taking the difference between the largest and the smallest values in a data set: RANGE = LARGEST VALUE – SMALLEST VALUE

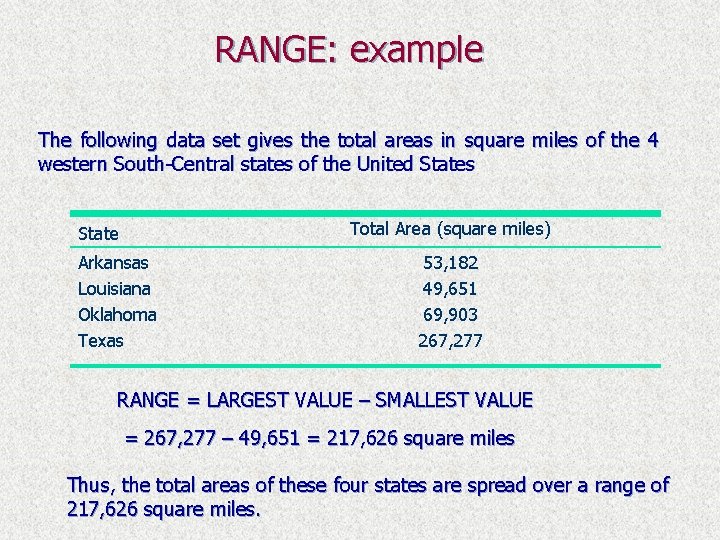
RANGE: example The following data set gives the total areas in square miles of the 4 western South-Central states of the United States Total Area (square miles) State Arkansas Louisiana Oklahoma Texas 53, 182 49, 651 69, 903 267, 277 RANGE = LARGEST VALUE – SMALLEST VALUE = 267, 277 – 49, 651 = 217, 626 square miles Thus, the total areas of these four states are spread over a range of 217, 626 square miles.

RANGE: disadvantages • The range, like the mean has the disadvantage of being influenced by outliers. Consequently, it is not a good measure of dispersion to use for data set containing outliers. • The calculation of the range is based on two values only: the largest and the smallest. All other values in a data set are ignored. • Thus, the range is not a very satisfactory measure of dispersion and it is, in fact, rarely used.

VARIANCE Definition The variance is a measure of dispersion of values based on their deviation from the mean. The variance is defined to be: for a population for a sample

VARIANCE The difference between an observation and the mean, ( or ) is called dispersion from the mean. Consequently, the variance can also be defined as the arithmetic mean of the squared deviations from the mean. From the computational point of view, it is easier and more efficient to use short-cut formulas to calculate the variance

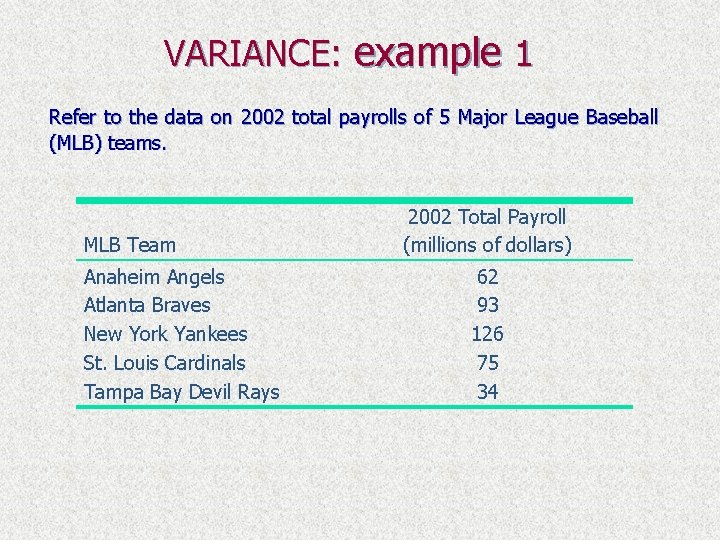
VARIANCE: example 1 Refer to the data on 2002 total payrolls of 5 Major League Baseball (MLB) teams. MLB Team Anaheim Angels Atlanta Braves New York Yankees St. Louis Cardinals Tampa Bay Devil Rays 2002 Total Payroll (millions of dollars) 62 93 126 75 34

VARIANCE: example 1 We apply the short-cut formula, hence we need to compute the squares of observations x 2. MLB Team Anaheim Angels Atlanta Braves New York Yankees St. Louis Cardinals Tampa Bay Devil Rays x x² 62 93 126 75 34 3844 8649 15, 876 5625 1156 ∑x = 390 ∑x² = 35150

VARIANCE: example 2 The following data are the 2002 earnings (in thousands of dollars) before taxes for all 6 employees of a small company. 48. 50 38. 40 65. 50 22. 60 x x² 48. 50 38. 40 65. 50 22. 60 79. 80 54. 60 2352. 25 1474. 56 4290. 25 510. 76 6368. 04 2981. 16 ∑x = 309. 40 ∑x² = 17977. 02 79. 80 54. 60

VARIANCE: frequency distribution The formula for variance changes slightly if observations are grouped into a frequency table. Squared deviations are multiplied by each frequency's value, and then the total of these results is calculated. for a population for a sample The short-cut formulas become:

VARIANCE: example 3 Vehicles Owned (xi) Number of Households (ni) 0 1 2 3 4 5 Sum xi * ni xi 2* ni 2 18 11 4 3 2 0 18 22 12 12 10 0 1 4 9 16 25 0 18 44 36 48 50 40 74 196

Variance: frequency distribution with classes Again, when the data set is organized in a frequency distribution with classes, we are approximating the data set by "rounding" each value in a given class to the class midpoint. Thus, the variance of a frequency distribution is given by Short-cut formulas for a population for a sample where mi is the midpoint of each class interval.

Variance: example 4 The following table gives the frequency distribution of the number of orders received each day during the past 50 days at the office of a mail-order company. Number of Orders 10 13 16 19 – – 12 15 18 21 Number of Days n m m 2 m*n m 2 *n 4 12 20 14 11 14 17 20 121 196 289 400 44 168 340 280 484 2352 5780 5600 ∑m*n = 832 ∑ m 2 *n = 14216 n= 50

STANDARD DEVIATION Definition The standard deviation is the positive square root of the variance. for a population for a sample

STANDARD DEVIATION The standard deviation is the most used measure of dispersion. The value of the standard deviation tells how closely the values of a data set are clustered around the mean. In general, a lower value of the standard deviation for a data set indicates that the values of that data set are spread over a relatively smaller range around the mean. In contrast, a large value of the standard deviation for a data set indicates that the values of that data set are spread over a relatively large range around the mean.

STANDARD DEVIATION: example 1 MLB Team Anaheim Angels Atlanta Braves New York Yankees St. Louis Cardinals Tampa Bay Devil Rays 2002 Total Payroll (millions of dollars) x x² 62 93 126 75 34 3844 8649 15, 876 5625 1156 ∑x = 390 ∑x² = 35150

STANDARD DEVIATION: example 2 Earnings (thousands of dollars) x x² 48. 50 38. 40 65. 50 22. 60 79. 80 54. 60 2352. 25 1474. 56 4290. 25 510. 76 6368. 04 2981. 16 ∑x = 309. 40 ∑x² = 17977. 02

Variance and Standard Deviation: observations The values of the variance and the standard deviation are never negative. That is, the numerator in the formula for the variance should never produce a negative value. Usually the values of the variance and standard deviation are positive, but if data set has no variation, then the variance and standard deviation are both zero. Example: 4 persons in a group are the same age – say 35 years. If we calculate the variance and the standard deviation, their values are zero.

CONTINGENCY TABLES AND ELEMENTS OF PROBABILITY

CONTINGENCY TABLES In many applications the interest is focused on the joint analysis of two variables (qualitative and/or quantitative) with the aim of evaluating the relation between them. The variables are usually presented as a contingency table (or two-way classification table). Whereas a frequency distribution provides the distribution of one variable, a contingency table describes the distribution of two or more variables simultaneously.

CONTINGENCY TABLES All 420 employees of a company were asked if they are smokers or nonsmokers and whether or not they are college graduates. Joint frequency of College Graduate Not a College Graduate Smoker 35 80 Nonsmoker 130 175 category “Smoker” of X and “Not a college Graduate” of Y Cell The table gives the distribution of 420 employees based on two variables or characters: X-smoke (yes or not) and Y-graduation (yes or not)

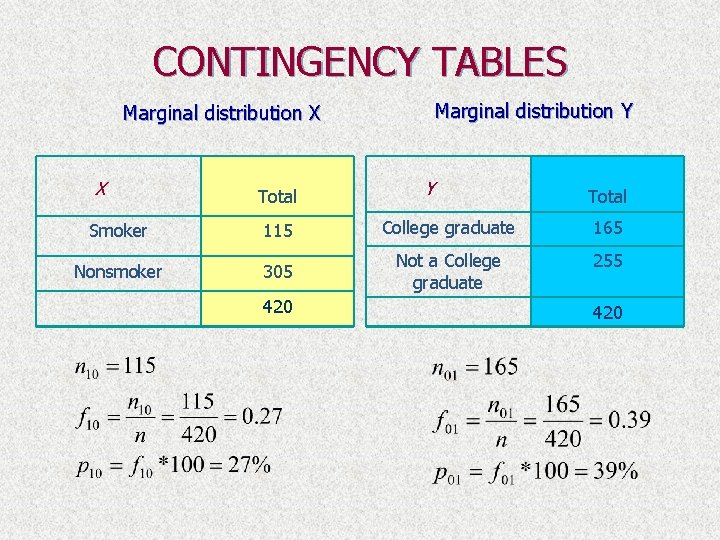
CONTINGENCY TABLES: marginal distributions Marginal distribution X College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420 X Marginal distribution Y Y Grand Total The right-hand column and the bottom row are called marginal distribution of X and marginal distribution of Y respectively.

CONTINGENCY TABLES Marginal distribution Y Marginal distribution X X Total Y Total Smoker 115 College graduate 165 Nonsmoker 305 Not a College graduate 255 420

CONTINGENCY TABLES: conditional distributions Conditional distribution of X to the category “College Graduate” of Y X Y College Graduate Conditional distribution of Y to the category “Smoker” of X Y X Smoker 35 College graduate 35 Nonsmoker 130 Not a College graduate 80 Total 165 Total 115 NOTE

Definition of probability There are three different definitions of probability: classical definition of probability, frequentist definition of probability, subjective (Bayesian) definition of probability. Frequentist definition of probability: The relative frequency associated to a category of a variable (event) analyzed can be interpreted as an approximation of the probability associated to that event.

Definition of probability Example: Ten of the 500 randomly selected cars manufactured at a certain auto factory are found to be lemons. Assuming that the lemons are manufactured randomly, what is the probability that the next car manufactured at this auto factory is a lemon? Car (xi) ni Relative frequency ( fi ) Good Lemon 490 10 490/500 =. 98 10/500 =. 02 n = 500 Sum = 1. 00 NOTE: The relative frequency is an approximation of the probability!! Relative frequencies and probabilities get closer as the number of cars increases.

Marginal Probability Coming back to the example of the 420 employees. Suppose that one employee is selected at random from the 420 employees. He may be classified on the basis of smoke alone or graduation. The employee can be “smoker”, “nonsmoker”, “graduate”, “nongraduate”. The probability of each characteristic is called marginal probability College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420

Marginal Probability Marginal (Simple) Probability: Probability is the probability frequency) computed on the marginal distributions: (relative College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420

Joint Probability Suppose that one employees is selected at random from these 420. What is the probability that the employee is a smoker and a College graduate? College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420 It is written as P (Smoker College Graduate). The symbol is read as “and”.

Joint Probability: is the probability (relative frequency) computed on the joint distributions College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420

Conditional Probability Now suppose that one employees is selected at random from these 420. Assume that it is known that he is a Smoker. What is the probability that the employee selected is Graduate? College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420 It is written as P (Graduate|Smoker) It is read as “Probability that he is College Graduate given that he is a Smoker”

Conditional Probability: is the probability (relative frequency) computed on the conditional distributions: College Graduate Not a College Graduate Total Smoker 35 80 115 Nonsmoker 130 175 305 Total 165 255 420