Scoring the Alignment of Amino Acid Sequences Constructing

Scoring the Alignment of Amino Acid Sequences Constructing PAM and Blosum Matrices

Quotes from page 11 of our Lab Manual: Proteins are huge molecules made up of large numbers of amino acids. The proteins are usually 100 to 500 amino acids long There are 20 different amino acids that make up the proteins

Name Abbr. Linear structure formula =========================== Alanine ala a CH 3 -CH(NH 2)-COOH Arginine arg r HN=C(NH 2)-NH-(CH 2)3 -CH(NH 2)-COOH Asparagine asn n H 2 N-CO-CH 2 -CH(NH 2)-COOH Aspartic acid asp d HOOC-CH 2 -CH(NH 2)-COOH Cysteine cys c HS-CH 2 -CH(NH 2)-COOH Glutamine gln q H 2 N-CO-(CH 2)2 -CH(NH 2)-COOH Glutamic acid glu e HOOC-(CH 2)2 -CH(NH 2)-COOH Glycine gly g NH 2 -COOH Histidine his h NH-CH=N-CH=C-CH 2 -CH(NH 2)-COOH Isoleucine ile i CH 3 -CH 2 -CH(CH 3)-CH(NH 2)Leucine leu l (CH 3)2 -CH-CH 2 -CH(NH 2)-COOH Lysine lys k H 2 N-(CH 2)4 -CH(NH 2)-COOH Methionine met m CH 3 -S-(CH 2)2 -CH(NH 2)-COOH Phenylalanine phe f Ph-CH 2 -CH(NH 2)-COOH Proline pro p NH-(CH 2)3 -CH-COOH Serine ser s HO-CH 2 -CH(NH 2)-COOH Threonine thr t CH 3 -CH(OH)-CH(NH 2)-COOH Tryptophan trp w Ph-NH-CH=C-CH 2 -CH(NH 2)-COOH Tyrosine tyr y HO-p-Ph-CH 2 -CH(NH 2)-COOH Valine val v (CH 3)2 -CH-CH(NH 2)-COOH

Constructing Probability Matrices Using a Smaller Set of AA’s Suppose we live in a world with only 3 amino acids: Alanine Leucine Serine Furthermore suppose: Alanine Leucine with probability. 2 Alanine Serine with probability. 1 Leucine Serine with probability. 3 We will assume that these probabilities are for changes that take place during one time unit

We can summarize these observations using the language of probability theory. We will use the notation (A|L, t) to mean: “A certain position in our sequence initially contains Leucine and at time, t, it contains Alanine. ” Another way of saying this is, “After t time units the position contains Alanine given that it initially contained Leucine. ” , i. e. the vertical bar means “given” So, Alanine given Leucine after t time units. We then write: Pr(A|A, 1) =. 7 Pr(A|L, 1) =. 2 Pr(A|S, 1) =. 1 Pr(L|A, 1) =. 2 Pr(L|L, 1) =. 5 Pr(L|S, 1) =. 3 Pr(S|A, 1) =. 1 Pr(S|L, 1) =. 3 Pr(S|S, 1) =. 6 The above can be summarized in a table, called a matrix 12 A L S A. 7. 2. 1 L. 2. 5. 3 S. 1. 3. 6

What about the probabilities two time units later? For example what is the probability that a position that was originally Alanine is Alanine two time units later? This can happen in three ways: A A A L A S A In our original notation, we are saying: (A|A, 2) = (A|A, 1)and(A|A, 1) or (L|A, 1)and(A|L, 1) or (S|A, 1)and(A|S, 1) Thus, to compute the probability, Pr(A|A, 2) = Pr(A|A, 1) + Pr(L|A, 1)Pr(A|L, 1) + Pr(S|A, 1)Pr(A|S, 1) =. 7*. 7 +. 2*. 2 +. 1*. 1 =. 49 +. 04 +. 01 =. 54 We will work out the 8 other second time unit transition probabilities in class.

After we compute all 9 of the probabilities for the transitions after 2 time units we have the following table. A L S A . 54 . 27 . 19 L . 27 . 38 . 35 S . 19 . 35 . 46 This table required three multiplications and two additions to compute the values placed in each of its nine cells. That is there where 27 multiplications and 18 additions required to produce the above table.

The Matrix Connection Consider the matrix, M, that we constructed earlier when we made the table of probabilities In matrix algebra, the product of two matrices is defined as follows: To compute the product of two matrices A and B, the value placed in row, i, and column, j, is obtained by multiplying each value in row, i, of A by its corresponding element in column, j, of B and summing the results. Translation by way of an illustration to follow.

Let’s suppose we want to square M, i. e. multiply M by itself To compute the value of the product matrix M 2 in row, 2, column, 3, we multiply each element in row 2 of the first matrix by its corresponding element in row 3 of the second matrix and sum the results: . 2*. 1 +. 5*. 3 +. 3*. 6 =. 02 +. 15 +. 18 =. 35 But this is exactly how we calculated Pr(S|L, 2)! This agreement between M 2 and the table of transition probabilities holds for each position. It appears that Matrix Multiplication is exactly what we need to generate the table of transition probabilities after t time units.

Thus, if we use the rules of matrix multiplication, Since the rules of matrix multiplication and those for computing the transition probabilities are essentially the same, we have a marriage made by the divine. So let’s use them to our advantage.

The number, variety, and chemical properties of the Amino Acids make the problem of scoring a pair of Amino Acids a much more complicated problem than scoring a pair of nucleotides. In the late 1970’s Dayhoff, Schwartz, and Orcutt decided to look at a database of similar proteins having common ancestors and obtain substitution frequency data. They looked at 71 groupings of protein data that differed by no more than 15% of their residues, i. e. at least 85% similar. They then built phylogenetic trees where each transition from generation to generation has as few changes as possible, given the data, in each ancestral sequence. From this a value is determined for the entry Aab in a matrix giving the frequency data for each pairing.

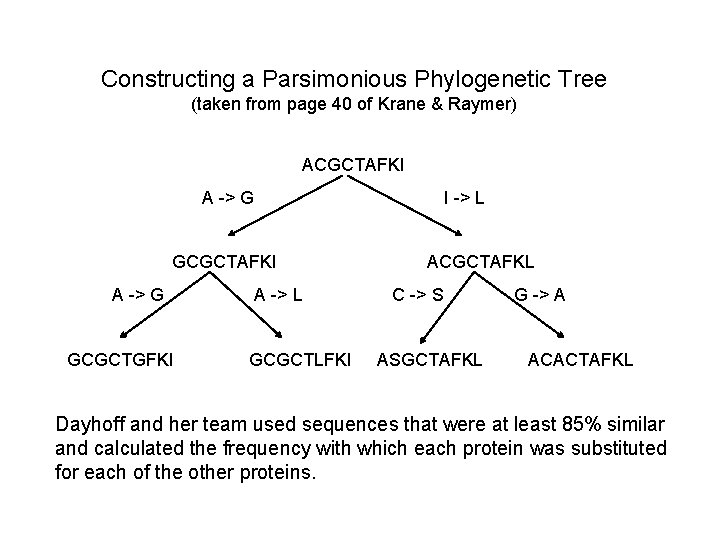
Constructing a Parsimonious Phylogenetic Tree (taken from page 40 of Krane & Raymer) ACGCTAFKI A -> G GCGCTGFKI A -> L GCGCTLFKI I -> L ACGCTAFKL C -> S ASGCTAFKL G -> A ACACTAFKL Dayhoff and her team used sequences that were at least 85% similar and calculated the frequency with which each protein was substituted for each of the other proteins.

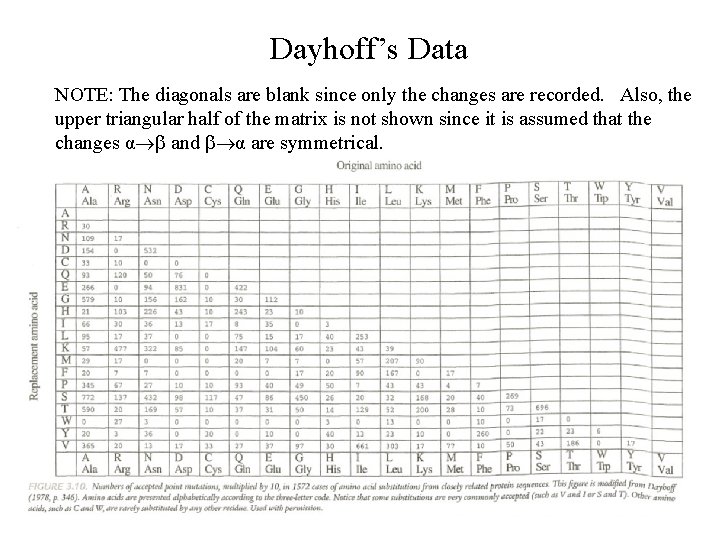
Dayhoff’s Data NOTE: The diagonals are blank since only the changes are recorded. Also, the upper triangular half of the matrix is not shown since it is assumed that the changes α and α are symmetrical.

Calculating the Entry in The Substitution Matrix Let P(b|a, t) = Probability that a is substituted for b in t time units adjusted for divergence time (Dayhoff time unit) qaqb = Probability that a would randomly follow b = (frequency if a)(freqency of b) s(a, b | t) = an entry at position (a, b) or (b, a) in the scoring matrix Then, s(a, b | t) =

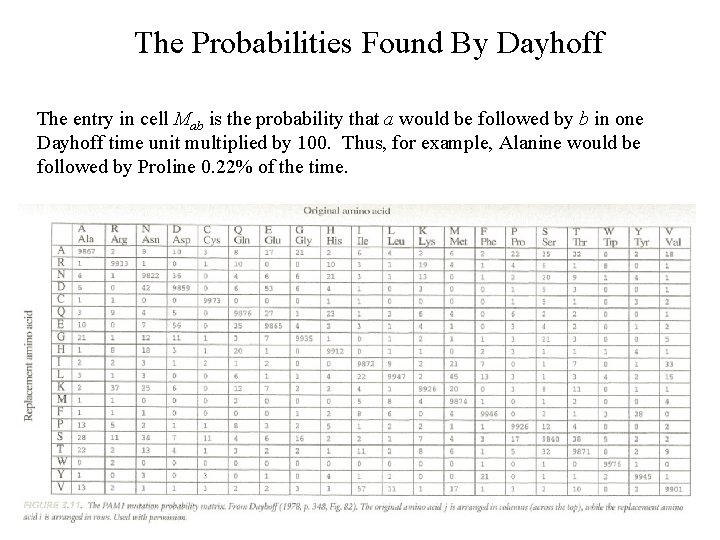
The Probabilities Found By Dayhoff The entry in cell Mab is the probability that a would be followed by b in one Dayhoff time unit multiplied by 100. Thus, for example, Alanine would be followed by Proline 0. 22% of the time.

Note: The previous matrix is NOT the scoring matrix. It is used to derive the scoring matrix. Recall: s(a, b | t) = However, the probability matrix is the main tool for deriving a sensible scoring matrix. To find the probability that amino acid a will mutate be replaced by amino acid b at a time t time units later, we need to calculate the a, b-th entry of the matrix Mt. After calculating this entry, then we apply the “log-odds” formula given above. The reason that the logarithm is used in the scoring formula is that it allows us, among other things, to add the scores of the aligned residues when we compute the score for an overall alignment of two sequences.

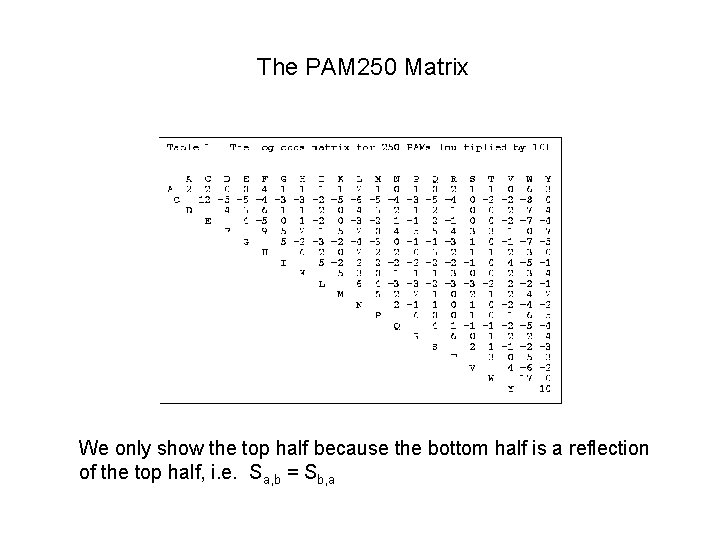
The matrix having scores found from the original probability matrix is called a 1 PAM matrix PAM stands for Point Accepted Mutation or Percent Accepted Mutation Dayhoff’s term was Accepted Point Mutation, but PAM rolls off the tongue easier than APM. The 1 means that given the degree of similarity between the sequences used to make up the matrix, the scores in this matrix are the frequencies for one evolutionary time unit. Scores representing longer times and are called PAMt matrices = Mt. The most widely used matrix is PAM 250 or the log-odds matrix based on: M 250 = the 250 th power of M. This matrix shows the probability of change over a long period of time. However, for closely related sequences, say mouse and rat MSH 2, a PAM 10 matrix may be more appropriate

The PAM 250 Matrix We only show the top half because the bottom half is a reflection of the top half, i. e. Sa, b = Sb, a

Discussion of PAM • The 1 PAM matrix was derived by constructing hypothetical phylogenetic trees relating sequences in 71 families. • The higher the power of the matrix, the more evolutionary time units represented by the matrix. • Criticism – raising M to high powers does not capture the true difference between short time substitutions and long time substitutions. • Note short time substitutions are dominated by amino acid substitutions that come from a single base change in the codon triplets of an Amino Acid, whereas the long time substitutions show all kinds of codon changes

BLOSUM (BLOck Substitution Matrix) Matrices

The criticism given at the end of the last discussion is that the large PAM matrices tend to minimize the effects of short time substitutions such as L<->I L<->V and Y<->F In 1991 – 1992 Henikoff and Henikoff used the BLOCKS database at the Fred Hutchison Cancer Research Center This database contains blocks of multiple alignments of more distantly related sequences Such a database can be used to derive scores more directly

Methodology • Sequences from each block were clustered • Two sequences were placed in the same cluster if their percent differences were above some level, say α% • The frequency Aab is calculated from observing residue a in one clustered alignment against residue b in another clustered alignment. • Corrections are made for clusters of differing sizes

Calculating the Matrix Entries Let the following be determined from the observed data: qa = the fraction of pairings that include an a pab = the fraction of parings of a and b Then and The score is calculated as These values are then scaled and rounded to make calculations easier.

If we set the limit, α, to 62, the we have a BLOSUM 62 Matrix

Most popular BLOSUM Matrices are BLOWSUM 62 and BLOWSUM 50. • BLOWSUM 62 is used mainly for ungapped matching. • BLOWSUM 50 is used for alignments with gaps. Note: the lower the number the longer the time span in evolutionary units.

Differences Between PAM and BLOSUM PAM assumes that substitutions probabilities for highly related proteins can be extrapolated to the probabilities for distantly related proteins. BLOWSUM matrices are based on the observation of more distantly related protein alignments. NOTE: Both types of matrices use log-odds values in their scoring systems.