Recapitulate We need to redefine momentum Introduced the










































- Slides: 48

Recapitulate • We need to redefine momentum. • Introduced the concept of four vector, by extending the concept of traditional vector.


Dot Product of Four Vectors Consider two four vectors, with components written in the frame S.

The dot product of these two four vectors is defined as follows.

Upon changing the frame to S’, the components of these four vectors would change as per the transformation matrix.

We, shall show that the dot product of the four vector would not change. This implies the following.





We, thus see that transformation ensures that the dot product of two four vectors does not change upon change of frame. Hence, it is a four scalar.

As a corollary of this we can define the length of a four vector as follows, which would also be a four scalar.

Example of a Four Vector x, y, z and ict are components of a four vector. This can be termed as position four vector.


Alternate Ways 1. Avoid imaginary number in transformation equation of four vector and correspondingly changes the definition of dot produce.

2. Put the fourth component as the first component and write transformation equation as follows.

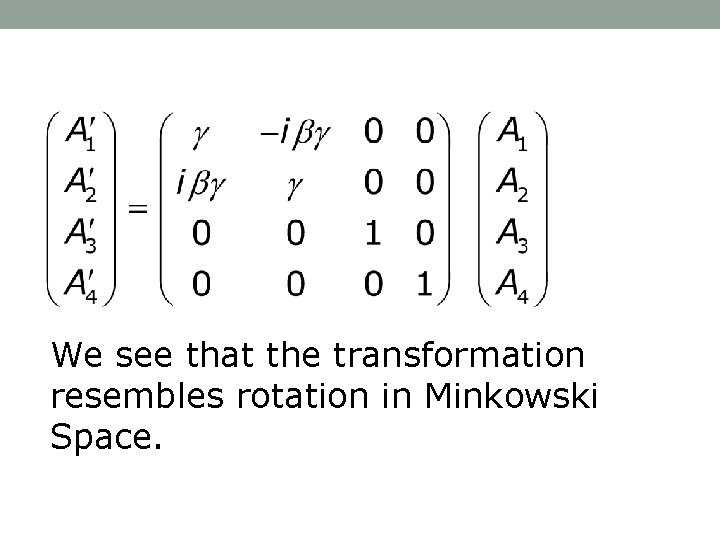
We see that the transformation resembles rotation in Minkowski Space.

Displacement Four Vector Imagine an event occurs at a position x 1, y 1, z 1 at a time t 1. Let at time t 2, another event occurs, the co-ordinates of which are x 2, y 2, z 2 in a frame S.

Δx=x 2 -x 1, Δy=y 2 -y 1, Δz=z 2 -z 1 and icΔt=ic(t 2 -t 1) shall also be components of four vector. This can be termed as displacement four vector.

Magnitude of Displacement The magnitude Δs of displacement four vector is given as follows. This is a four scalar and its value would be same in all inertial frames.

Proper Time Interval The proper time interval Δ , another four scalar, between these two events is given as follows.

1. This definition is more general definition of proper time interval and is consistent with the older definition. 2. For space like separated events the proper time interval is imaginary. It is real for time like separated events.

Example 1 Consider Two events in a frame S at the following co-ordinates. E 1: x 1=150 m, t 1=0. 3 s E 2: x 2=210 m, t 2=0. 4 s


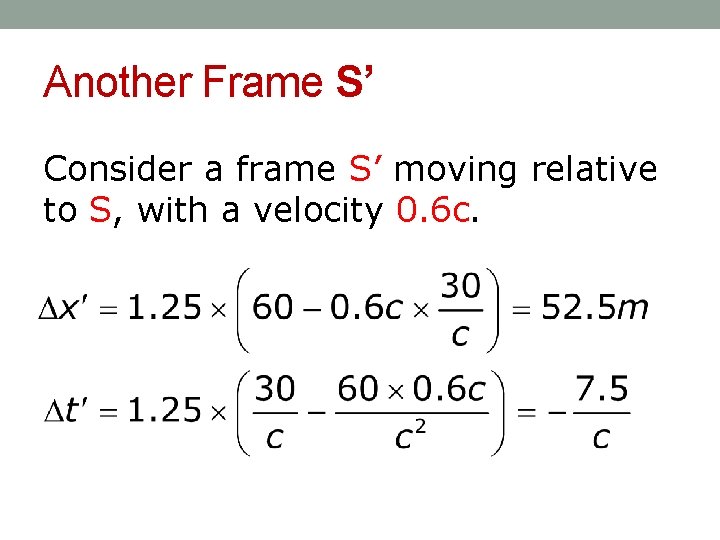
Another Frame S’ Consider a frame S’ moving relative to S, with a velocity 0. 6 c.


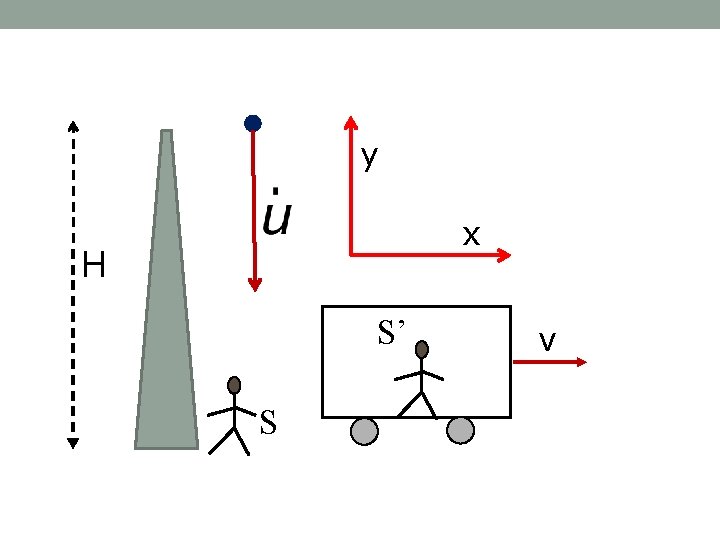
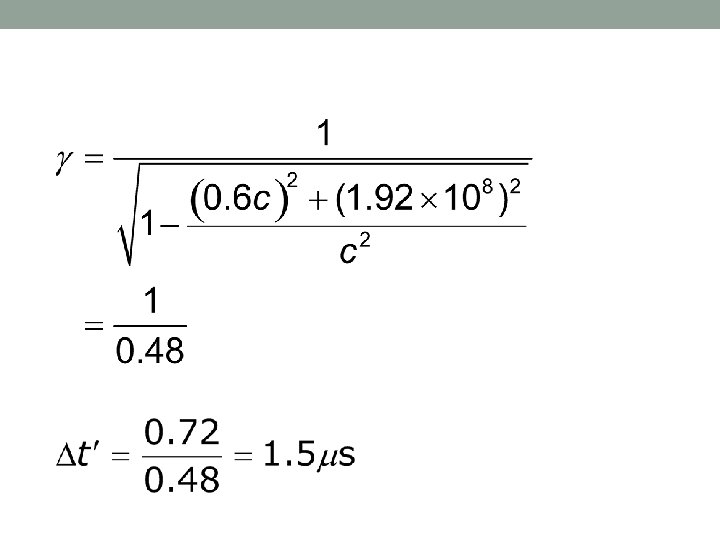
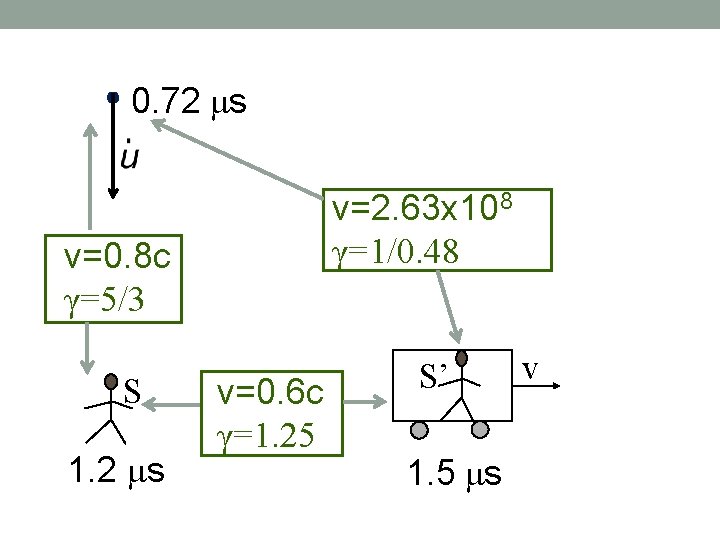
Example 2 An object is moving in S frame in -y direction with a constant velocity and travels a fixed tower of height 288 m in 1. 2 s. Find the proper time interval for crossing the tower. Verify that it is unchanged in a frame S’ which is moving in +x direction with a speed 0. 6 c.

y x H S’ S v

E 1: x 1=0, y 1= 288 m, t 1=0 E 2: x 2=0, y 2=0, t 2= 1. 2 μs

In S’

Note We note that, even though Δt is not a proper time interval The use of time dilation formula requires only x co-ordinate to be same.


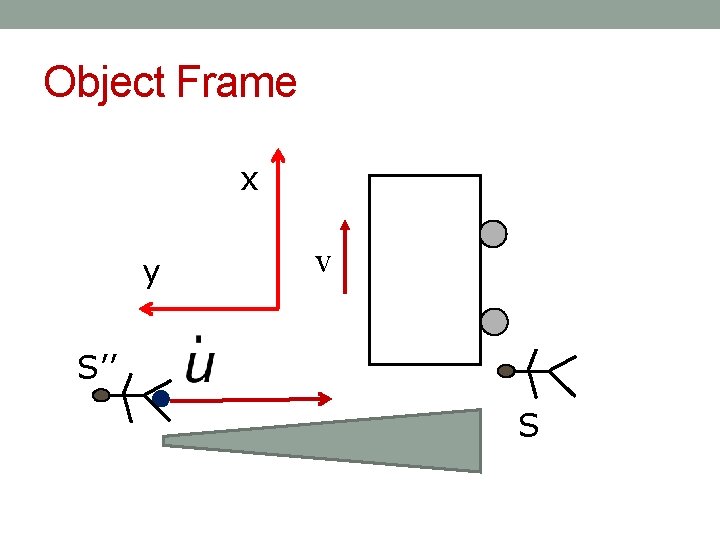
Object Frame x y v S’’ S

We see that the relative velocity of frame S” is in –y direction. The Lorentz transformation for this case would, therefore, be written as follows.



Time Dilation S” to S

Time Dilation S” to S’ Find speed of S’ in S’’ frame or of S’’ in S’ frame.



0. 72 μs v=2. 63 x 108 γ=1/0. 48 v=0. 8 c γ=5/3 S 1. 2 μs v=0. 6 c γ=1. 25 S’ 1. 5 μs v

Velocity Four Vector Imagine that the two events are related to motion of a particle. Imagine a particle is located at a position x 1, y 1, z 1 at a time t 1. Later at time t 2, it is found at co-ordinates x 2, y 2, z 2. Both observations are made in a frame S.

We realize that Δx, Δy, Δz and icΔt are the components of a four vector. However, once they are divided byΔt, they cease to be so.

However, if we divide by a four scalar Δ instead of Δt, we shall be able retain them as components of four vector.

Velocity Four Vector Component We can find the components in a frame by multiplying ux, uy, uz and ic by .


The Components of velocity four vector are thus given by

Transformation
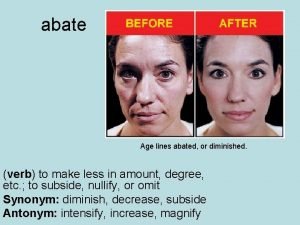
 Abate antonym
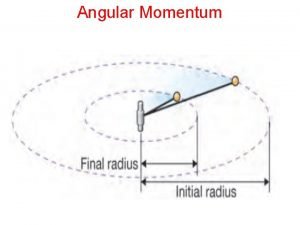
Abate antonym Conceptual physics momentum
Conceptual physics momentum Rtf to tiff
Rtf to tiff Uac nsw
Uac nsw Mandate of heaven ancient china
Mandate of heaven ancient china Erd simbol
Erd simbol Life is a highway metaphor
Life is a highway metaphor Term biodiversity was coined by
Term biodiversity was coined by Twenty point program
Twenty point program History of sonnet
History of sonnet Introduced by
Introduced by Who sponsored house bill 393
Who sponsored house bill 393 When was mpls introduced
When was mpls introduced Peter introduced me to jack
Peter introduced me to jack Dewey decimal system
Dewey decimal system He introduced the ppft
He introduced the ppft They introduced me to her husband passive voice
They introduced me to her husband passive voice Customs of england
Customs of england As kayla was introduced
As kayla was introduced Fad
Fad Early beginnings of tourism
Early beginnings of tourism What is not a classical accompaniment of poulet maryland
What is not a classical accompaniment of poulet maryland Doppler radar was introduced in_______.
Doppler radar was introduced in_______. Define dental auxiliary
Define dental auxiliary Archibald maclaren physical education
Archibald maclaren physical education C introduced by
C introduced by Structuralism psychology definition
Structuralism psychology definition Lord cornwallis introduced
Lord cornwallis introduced Bayan-anihan president
Bayan-anihan president It was introduced by chen in 1976
It was introduced by chen in 1976 Flag football
Flag football Conclusion of delhi sultanate
Conclusion of delhi sultanate First generation of rights
First generation of rights What conflict is introduced in this excerpt? justin lebo
What conflict is introduced in this excerpt? justin lebo Inter bank participation
Inter bank participation Thể thơ truyền thống
Thể thơ truyền thống Hát lên người ơi alleluia
Hát lên người ơi alleluia Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Lời thề hippocrates
Lời thề hippocrates Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công của trọng lực
Công của trọng lực Môn thể thao bắt đầu bằng chữ f
Môn thể thao bắt đầu bằng chữ f