Quantum Algorithms a survey Umesh V Vazirani U

Quantum Algorithms: a survey Umesh V. Vazirani U. C. Berkeley

Exponential Superposition + - + + - - + - § Superposition of all 2 n classical states: § Measurement: all n-bit strings See |xi with probability |ax|2 Quantum Algorithms: tension between these two phenomena

Why limit computers to electronics implemented on silicon? • Extended Church Turing thesis - Any “reasonable” model of computation can be efficiently simulated by a probabilistic Turing Machine. - Circuits, Random access machines, cellular automata. - “Reasonable” = physically realizable in principle • Quantum computers only model that violate this thesis

Quantum Algorithms – Exponential Speedups • Shor’s quantum factoring algorithm. Breaks modern cryptography. • Simulating quantum mechanics. • Symmetry - Discrete logarithm - Pell’s equation - Shifted Legendre Symbol - Gauss sums - Elliptic curve cryptography

Young’s Double slit experiment P 1(x) = |F 1(x)|2 P 2(x) = |F 2(x)|2 F 1, 2 = F 1(x) + F 2(x) P 1, 2(x) = |F 1, 2(x)|2

n-slits • Etch n slits in a pattern based on the input. • Send photon through and measure. • Location at which photon detected gives provides information about solution to input. photon Input-based slit pattern screen

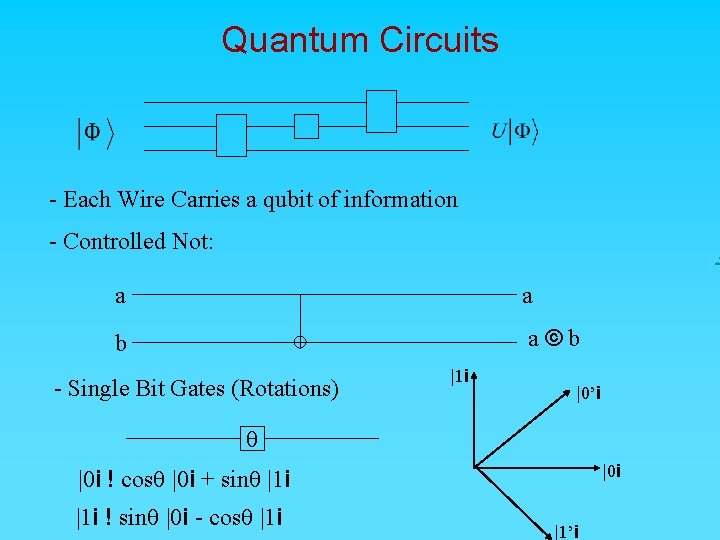
Quantum Circuits - Each Wire Carries a qubit of information - Controlled Not: . . a a b a©b - Single Bit Gates (Rotations) |1 i |0’i q |0 i ! cosq |0 i + sinq |1 i ! sinq |0 i - cosq |1 i |1’i

Quantum Fourier Transform Classical: FFT O(m logm) Quantum: Input: |Fi = åj=0 m aj |ji O(logm) qubits Fourier transform: F|Fi = åj=0 m 1 bj |ji O(log 2 m) gates Limited Access: Measure: see |ji with probability |bj|2

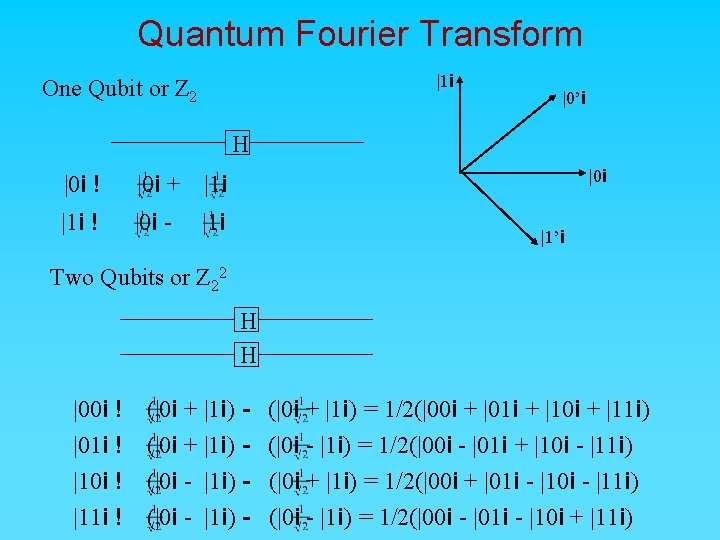
Quantum Fourier Transform |1 i One Qubit or Z 2 |0’i H |0 i ! |0 i + |1 i ! |0 i - |1 i |0 i |1’i Two Qubits or Z 22 H H |00 i ! |01 i ! |10 i ! |11 i ! (|0 i + |1 i) (|0 i - |1 i) (|0 i + |1 i) = 1/2(|00 i + |01 i + |10 i + |11 i) (|0 i - |1 i) = 1/2(|00 i - |01 i + |10 i - |11 i) (|0 i + |1 i) = 1/2(|00 i + |01 i - |10 i - |11 i) (|0 i - |1 i) = 1/2(|00 i - |01 i - |10 i + |11 i)

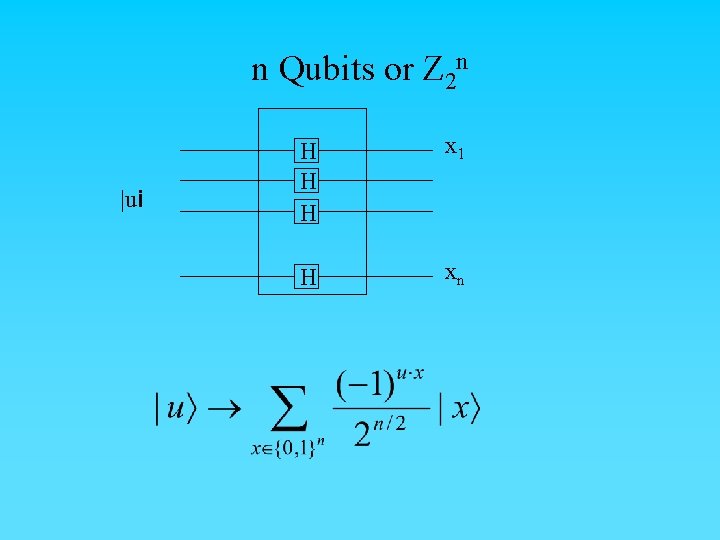
n Qubits or Z 2 n |ui H H H x 1 H xn

Outline of Shor’s Factoring Algorithm • N ! exponential superposition åx ax |xi • Factors of N encoded in global property of superposition – its period. • quantum fourier transform and measure to extract period. • Reconstruct factors of N from the period. 0 q

Outline of Shor’s Factoring Algorithm (Example) • N = 15 = p¢ q • Randomly choose a = 7 (mod 15) • Consider sequence ax (mod 15) for x =0, 1, 2, … 1, 7, 4, 13, … • Period r = 4. • N | (ar-1)=(ar/2+1)(ar/2 -1) = (72 +1)(72 -1) = 50¢ 48 • p = gcd(15, 50), q = gcd(15, 48). • Create superposition åx |xi |axi 0 q

Outline of Shor’s Factoring Algorithm (Example) • N = 15 = p¢ q • Randomly choose a = 7 (mod 15) • Consider sequence ax (mod 15) for x =0, 1, 2, … 1, 7, 4, 13, … • Period r = 4. N | (r+1)(r-1) = (4+1)(4 -1) = 5¢ 3 • p = gcd(15, 5), q = gcd(15, 3). • Create superposition åx |xi |axi 0 q

The Hidden Subgroup Problem Given f : G ! S, constant and distinct on cosets of subgroup H. Find H. G: Examples • Factoring N: G = • Discrete log: G =

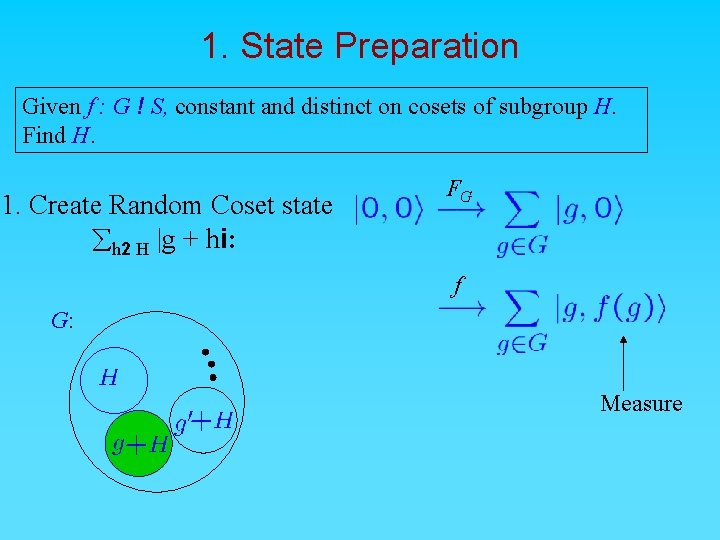
1. State Preparation Given f : G ! S, constant and distinct on cosets of subgroup H. Find H. 1. Create Random Coset state åh 2 H |g + hi: FG f G: Measure

2. Fourier Sampling G: F. T. Measure a random element of H? . 3) (Classically) reconstruct H from polynomialy many samples.

Example: Factoring To factorize N = P¢Q, sufficient to compute order of randomly chosen x mod N. i. e. smallest positive r: xr = 1 mod N. Let f: a ! xa mod N. Underlying group = ZM, where M = F(N) = (P-1)¢(Q 1) Hidden subgroup = H = h r i = {0, r, 2 r, …, M/r} H? = h M/ri = {0, M/r, 2 M/r, …, M} Fourier sampling gives k. M/r for random k: 0 · k · r-1 gcd(M, k. M/r) = M/r if k, r relatively prime.

Pell’s Equation • Given a positive non-square integer d, find integer solutions x, y of x 2 – d¢ y 2 = 1. • One of the oldest studied problem in algorithmic number theory. • Appears harder than factoring • [1989] Buchman-Williams cryptosystem • [Hallgren 2002]: 1) Quantum algorithm for Pell’s Equation 2) Breaks Buchman-Williams cyptosystem Abelian Hidden subgroup problem – but the group is not finitely generated

Two Challenges Short vector in Lattice: • Basis v 1, …, vn vectors in Rn. • The lattice is a 1 v 1 + … + an vn for all integers a 1, … an. • Find shortest vector in lattice.

Two Challenges 1. Short vector in Lattice: Finding short vector not easy! Regev: DN Dihedral group 2. Graph Isomorphism SN Symmetric group

Ajtai-Dwork Cryptosystem.

[GSVV] For random choice of basis, for sufficiently non-abelian groups (e. g. S_n), exponentially many samples necessary to distinguish |H|=2 from |H| =1.

Dihedral HSP • Dihedral Group DN : Group of symmetries of a regular N-gon. • Generated by x, y: x. N = 1, y 2=1, xyxy = 1. • Assume N = 2 n. • DN has 4 1 -d irreps and (N-1)/2 2 -d irreps. [Kuperberg ’ 03] algorithm for dihedral HSP.

Dihedral HSP algorithm • Assume wlog H = {1, xhy} • Set up random coset state, fourier transform and sample irrep to get random j, • Can sample column superposition and do phase estimation to get coin flip of bias • O(log N) samples sufficient to determine h, but reconstruction problem hard. • Would like to sample particular irreps j.

Dihedral HSP algorithm Claim: ri rj = ri+j © ri j Algorithm: • Start with registers in random coset states, FT, sample irreps. • Sort irrep names, pair up successive registers • Apply above transformation, and retain iff i, j ! i j • Number of bits reduced by per iterations • Number of irreps reduced by 4 per iteration.

Non-abelian Hidden Subgroup Problem • Abelian quantum algorithm doesn’t generalize - Prepare random coset state - Measure in Fourier basis • Ettinger, Hoyer, Knill ’ 98: - Prepare several registers with random coset states - Perform appropriate joint measurement • Ip ’ 03: - Fourier transform & Measure irrep (character) for each register - Perform appropriate joint measurement on residual state.

Adiabatic Quantum State Generation Aharonov, Ta-Shma ‘ 02 Aharonovvan. Dam. Kempe. Landau. Lloyd. Regev’ 03 Adiabatic Computation ≈ Quantum Computation

Classical Simulation of Quantum Systems Vidal ’ 03 Polynomial time simulation of one dimensional spin chains with O(log n) entanglement length. r. AC = r. A r. C A 1 r. ABC = r. AB 1 r. B 2 C B 2 C

Summary • Quantum computation only model that violates extended Church-Turing thesis. • Exponential superposition vs limited access. • Exponential speedups appear to require symmetry. • Fast quantum algorithm for abelian hidden subgroup problem • Non-abelian case open.