Progressive Simplicial Complexes Jovan Popovic Hugues Hoppe Carnegie

Progressive Simplicial Complexes Jovan Popovic Hugues Hoppe Carnegie Mellon University Microsoft Research

Complex Models • Rendering • Storage • Transmission 232, 974 faces

Previous Work Progressive Meshes 150 152 M 0 vspl 0 [Hoppe, ‘ 96] 500 M 1 13, 546 M 175 … vspli … vspln-1 Progressive Mesh (PM) representation ^ n M =M

PM Features Continuous LOD sequence Smooth visual transitions (Geomorphs) Progressive transmission Space-efficient representation

PM Restrictions Supports only “meshes” (orientable, 2 -dimensional manifolds) Would also like:

PM Restrictions Supports only “meshes” (orientable, 2 -dimensional manifolds) Preserves topological type M 0 Mn

PM Restrictions Supports only “meshes” (orientable, 2 -dimensional manifolds) Preserves topological type M 0 2, 522 … Mi … 8, 000 Mn 167, 744

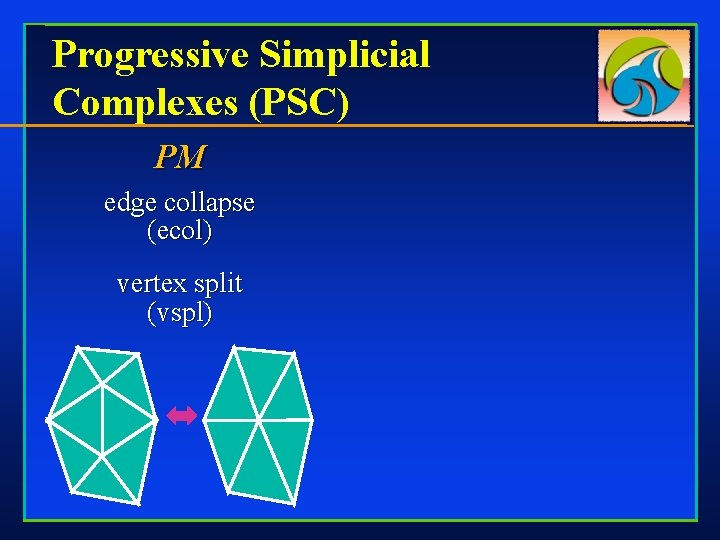
Progressive Simplicial Complexes (PSC) PM edge collapse (ecol) vertex split (vspl)

Previous Work Vertex unification schemes [Rossignac-Borrel ‘ 93] [Schaufler-Stürzlinger ‘ 95]

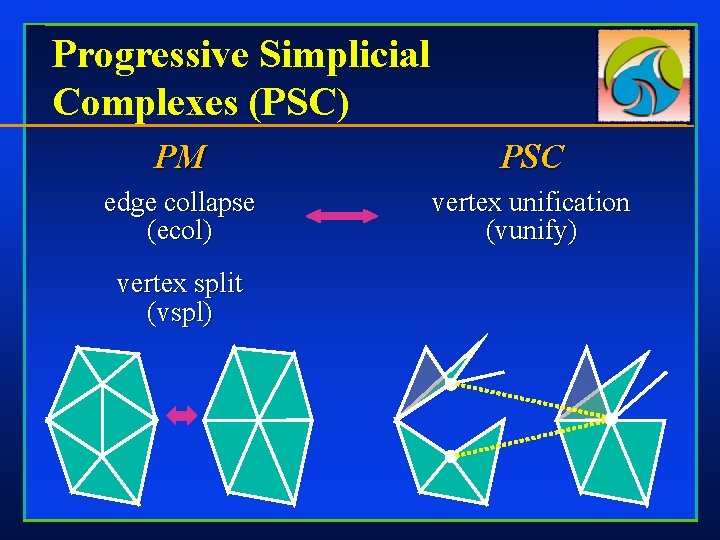
Progressive Simplicial Complexes (PSC) PM PSC edge collapse (ecol) vertex unification (vunify) vertex split (vspl)

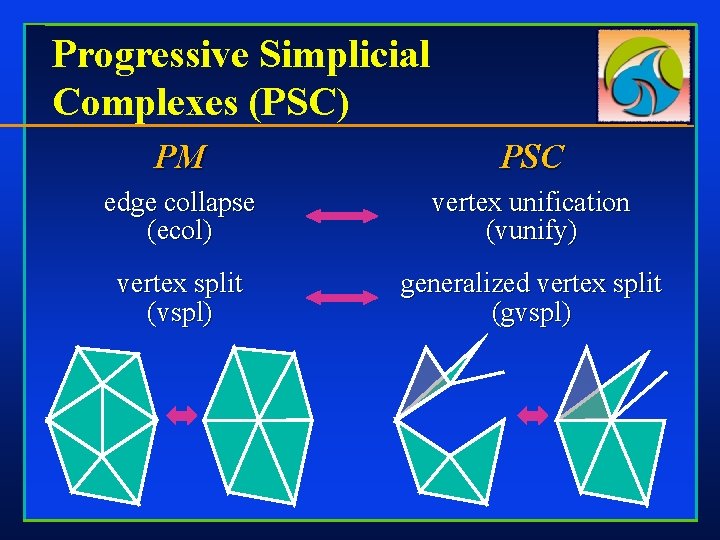
Progressive Simplicial Complexes (PSC) PM PSC edge collapse (ecol) vertex unification (vunify) vertex split (vspl) generalized vertex split (gvspl)

Simplicial Complex ^ M V K

Simplicial Complex ^ M V K

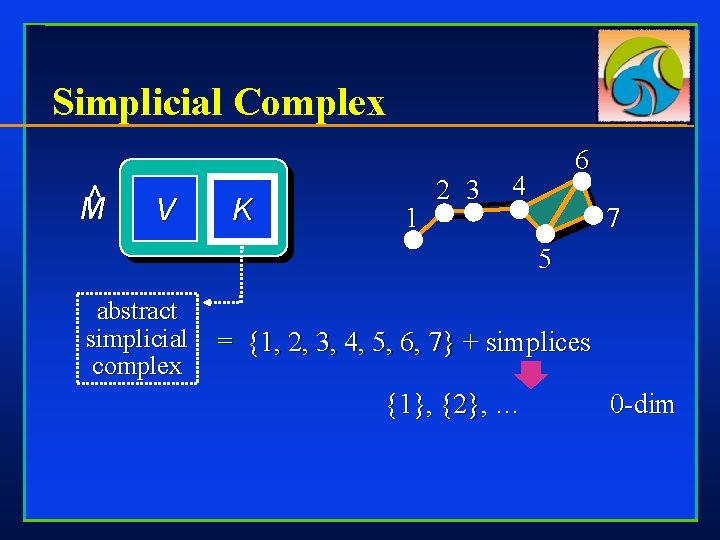
Simplicial Complex ^ M V K 1 2 3 6 4 7 5 abstract simplicial complex = {1, 2, 3, 4, 5, 6, 7} + simplices {1}, {2}, … 0 -dim

Simplicial Complex ^ M V K 1 2 3 6 4 7 5 abstract simplicial complex = {1, 2, 3, 4, 5, 6, 7} + simplices {1}, {2}, … {1, 2}, {2, 3}… 0 -dim 1 -dim

Simplicial Complex ^ M V K 1 2 3 6 4 7 5 abstract simplicial complex = {1, 2, 3, 4, 5, 6, 7} + simplices {1}, {2}, … {1, 2}, {2, 3}… 0 -dim 1 -dim {4, 5, 6}, {6, 7, 5} 2 -dim

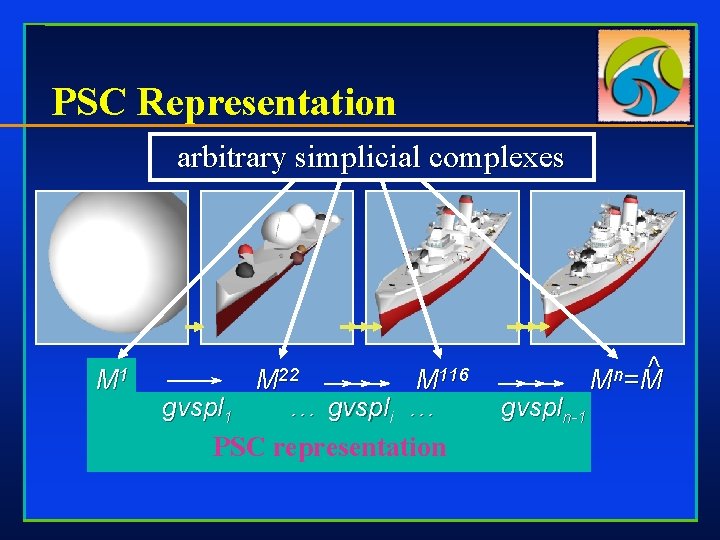
PSC Representation arbitrary simplicial complexes M 1 gvspl 1 M 22 M 116 … gvspli … PSC representation gvspln-1 ^ Mn=M

PSC Features Video Destroyer PSC sequence PM, PSC comparison PSC Geomorphs Line Drawing

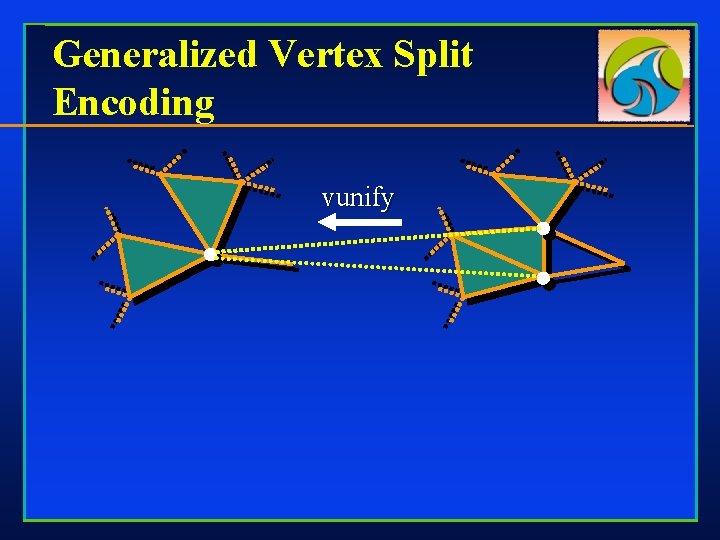
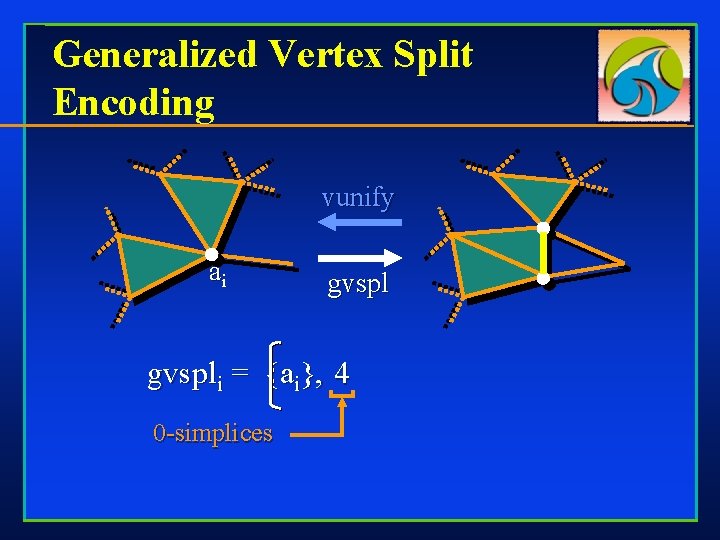
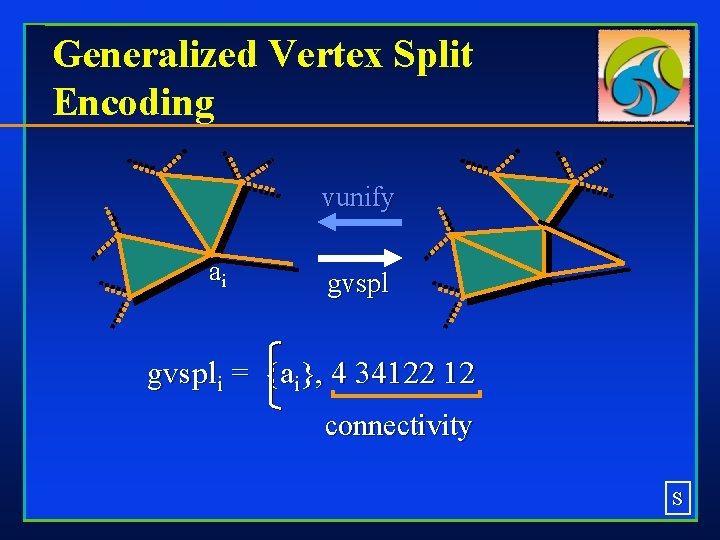
Generalized Vertex Split Encoding vunify

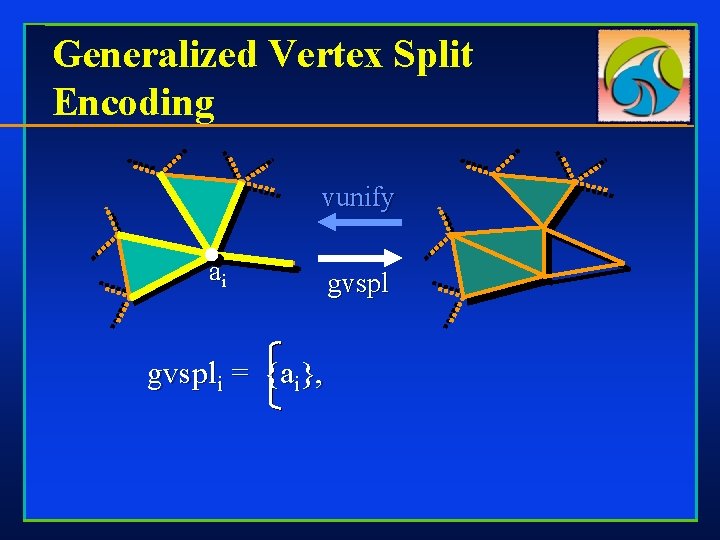
Generalized Vertex Split Encoding vunify ai gvspli = {ai}, gvspl

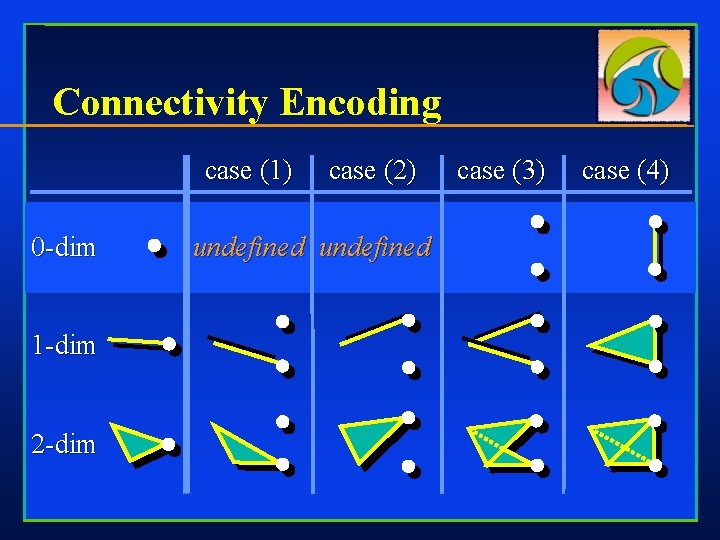
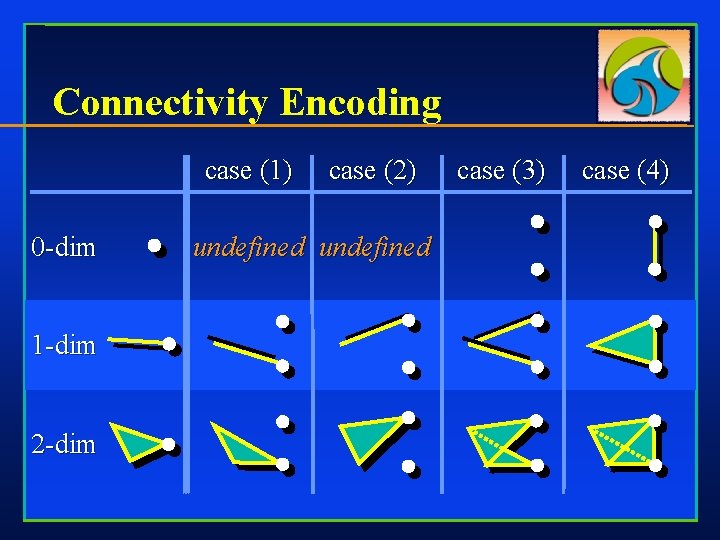
Connectivity Encoding case (1) 0 -dim 1 -dim 2 -dim case (2) undefined case (3) case (4)

Connectivity Encoding case (1) 0 -dim 1 -dim 2 -dim case (2) undefined case (3) case (4)

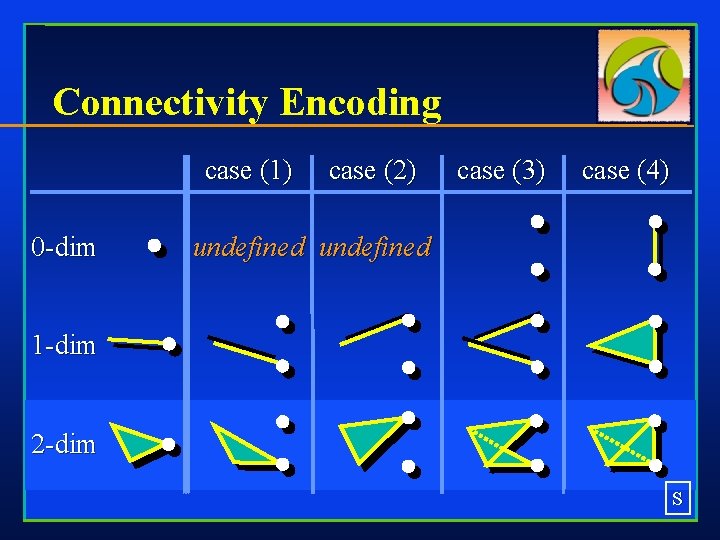
Connectivity Encoding case (1) 0 -dim case (2) case (3) case (4) undefined 1 -dim 2 -dim S

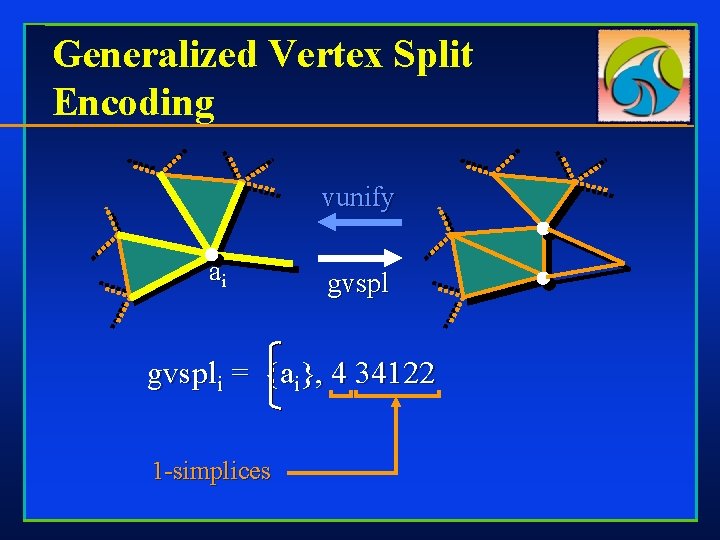
Generalized Vertex Split Encoding vunify ai gvspli = {ai}, 4 0 -simplices

Generalized Vertex Split Encoding vunify ai gvspli = {ai}, 4 34122 1 -simplices

Generalized Vertex Split Encoding vunify ai gvspli = {ai}, 4 34122 12 2 -simplices

Generalized Vertex Split Encoding vunify ai gvspli = {ai}, 4 34122 12 connectivity S

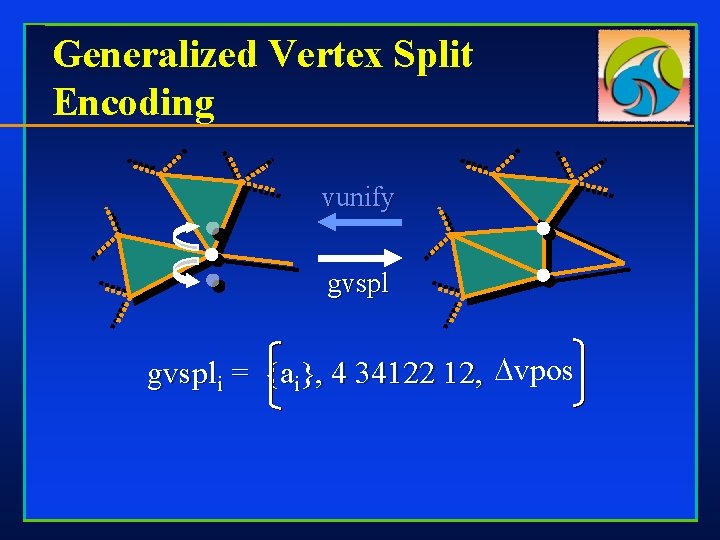
Generalized Vertex Split Encoding vunify gvspli = {ai}, 4 34122 12, vpos

Connectivity Encoding Analysis vunify gvspl example: 15 bits models (avg): 30 bits 3 4 11111 22222 33333 44444 11 22 33 44

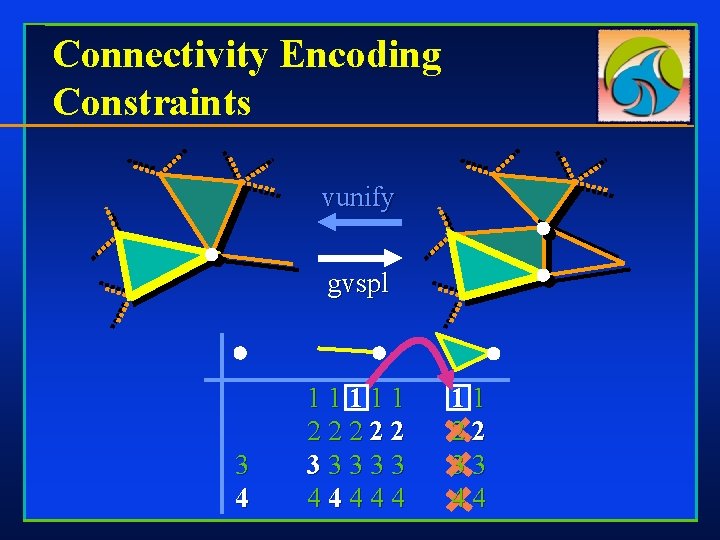
Connectivity Encoding Constraints vunify gvspl 3 4 11111 22222 33333 44444 11 22 33 44

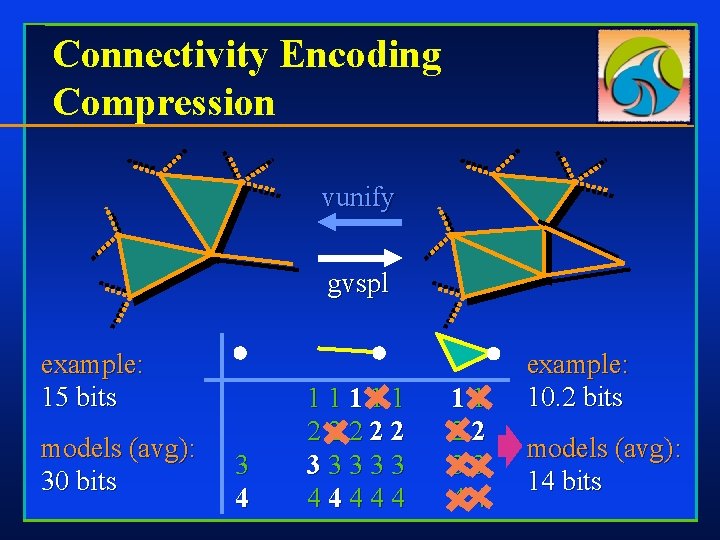
Connectivity Encoding Compression vunify gvspl example: 15 bits models (avg): 30 bits 3 4 11111 22222 33333 44444 11 22 33 44 example: 10. 2 bits models (avg): 14 bits

Space Analysis Average 2 D manifold mesh n vertices, 3 n edges, 2 n triangles PM representation n ( log 2 n + 4 ) bits PSC representation n ( log 2 n + 7 ) bits

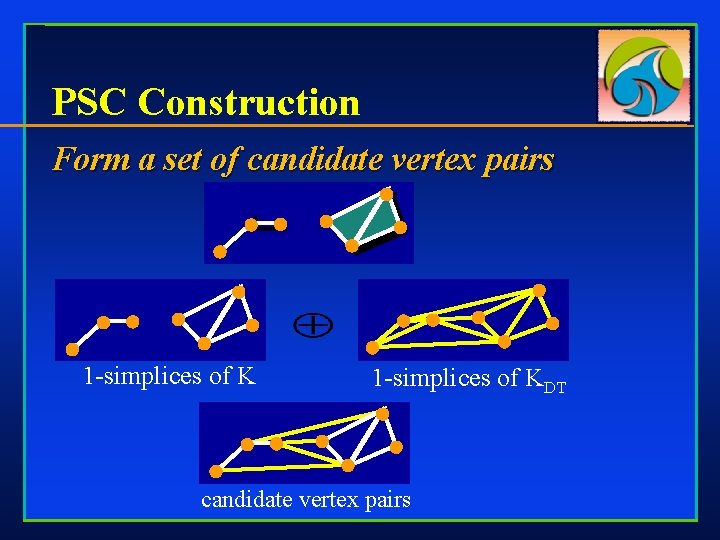
PSC Construction Form a set of candidate vertex pairs 1 -simplices of KDT candidate vertex pairs

PSC Construction Form a set of candidate vertex pairs • 1 -simplices of KDT Compute cost of each vertex pair • ∆E = ∆Edist + ∆Edisc + E∆area + Efold Unify pair with lowest cost • updating costs of affected candidates

Simplification Results 72, 346 triangles 674 triangles

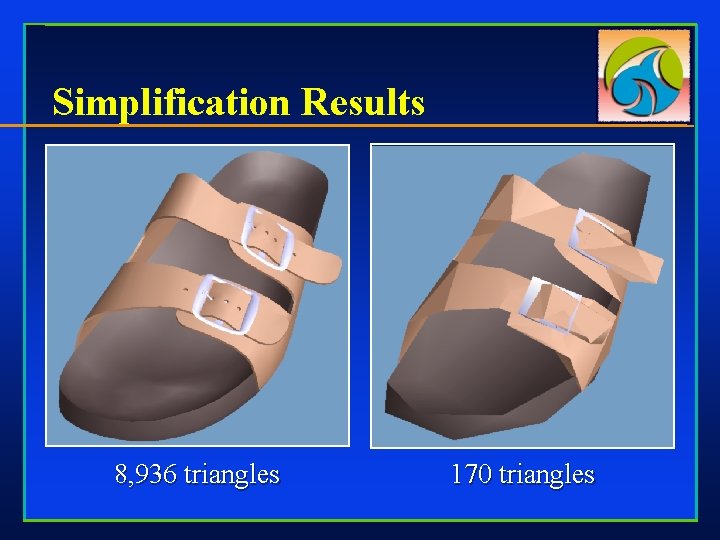
Simplification Results 8, 936 triangles 170 triangles

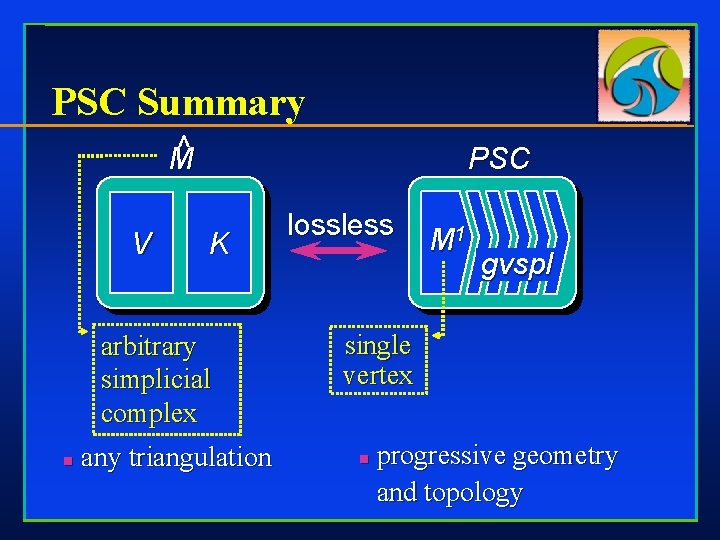
PSC Summary ^ M V PSC K arbitrary simplicial complex n any triangulation lossless M 1 gvspl single vertex n progressive geometry and topology

PSC Summary Continuous LOD sequence Smooth transitions (Geomorphs) Progressive transmission Space-efficient representation Supports topological changes Models of arbitrary dimension e. g. LOD in volume rendering