SOCIAL NETWORKS AND SIMPLICIAL COMPLEXES IN HONOR OF






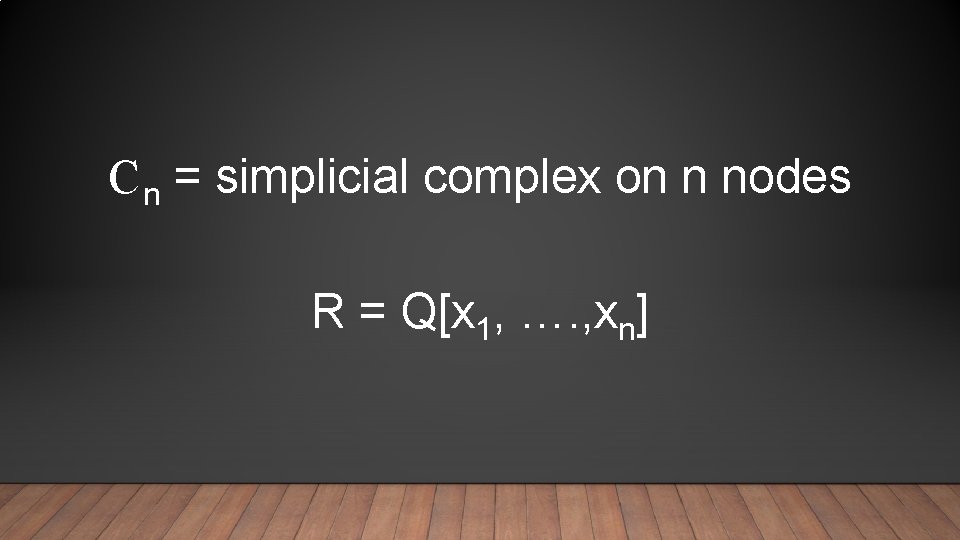












- Slides: 20

SOCIAL NETWORKS AND SIMPLICIAL COMPLEXES (IN HONOR OF ED WEGMAN) DANIELE STRUPPA CHAPMAN UNIVERSITY

STARTING POINT • Many (social) phenomena cannot be efficiently described by graphs (networks) • Example: papers coauthorship B B A, B: Paper 1 A, B, C: Paper 1 B, C: Paper 2 A, C: Paper 3 A C

HYPERGRAPHS • In a graph, an edge only join two vertices, while in a hypergraph an edge (or hyperedge) can join any number of vertices. • Hypergraphs are examples of incidence structures. • An important example of hypergraphs is given by abstract simplicial complexes, which are hypergraphs that contain all subsets of every edge.

SIMPLICIAL COMPLEXES • A set composed of points, line segments, triangles, tetrahedra, and their n-dimensional analogs. • From a purely combinatorial point of view they are referred to as simplicial complexes.

SOME QUESTIONS ON NETWORKS: CAN THEY BE EXTENDED TO HYPERGRAPHS AND SIMPLICIAL COMPLEXES? • Centrality measures (Identification of thought leaders) • Random networks (Evolution of social systems) • Applications to a wide variety of settings (from social sciences to natural sciences)

POLYNOMIAL ALGEBRA FOR SIMPLICIAL COMPLEXES Node Variable Face Monomial of Nodes in the Face
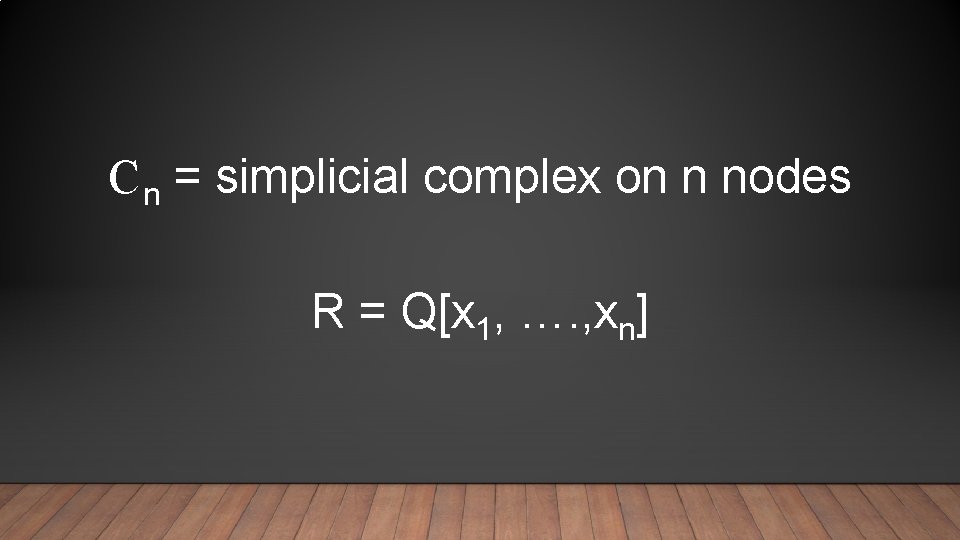
C n = simplicial complex on n nodes R = Q[x 1, …. , xn]

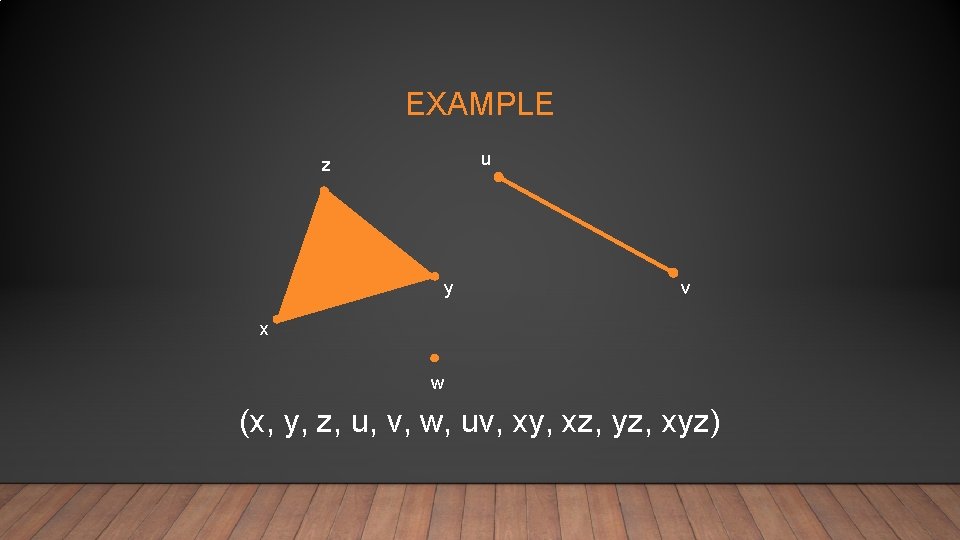
EXAMPLE u z y v x w (x, y, z, u, v, w, uv, xy, xz, yz, xyz)

FACE RING Stanley-Reisner ideal I is the ideal generated by faces not in the complex. We associate to this ideal the face ring of the simplicial complex defined by F I : = Q [x 1, ……, xn]/ I

EXAMPLE z u y v x w I = {xu, xv, xw, yu, yv, yw, zu, zv, zw, uw, vw} But what about xyw? Minimality

FACET RING Facet ideal L is the ideal generated by maximal faces (facets), i. e. faces not contained in faces of higher dimension, and the facet ring is the quotient defined by F L : = Q [x 1, ……, xn]/ L

EXAMPLE z u y v x w J = {xyz, uv, w}

KEY IDEA • Quotients of rings of polynomials can be described in terms of algebraic invariants, which give important information on the associated simplicial complexes • The theory of Grobner bases allows explicit calculation of these invariants • These invariants, in turn, may shed light on the social structure described by the simplicial complex

THE CASE OF THE FACE RING OF A SIMPLICIAL COMPLEX C • Connectedness and high-dimensional holes are topological properties of the complex C that have important meaning in the social context • These objects can be calculated through the dimension of the homology groups of the Stanley-Reisner ideal associated to the dual of C • The Hilbert series of C, H(z) = h(n)z/(1 -z)d and its coefficients can offer additional understanding on its structure

THE SYZYGIES OF THE FACET IDEAL OF A COMPLEX C • If L is the facet ideal generated by r monomials m 1, …mr, we can compute its syzygies, i. e. the submodule of Rr generated by (s 1, …sr) such that m 1 s 1+…mrsr=0, and then the minimal graded free resolution of L. that can be obtained by constructing the syzygies of the syzygies, etc. • These algebraic objects are a good descriptor of the connectedness of the faces of the complex C. • For example, if a syzygy between two facets appears as a minimal generator of the ideal of syzygies, then the two facets are either connected by a common face, or are totally separated, but if the syzygy is not a minimal generator, then the facets are connected by at least one face, but not directly connected.

EXAMPLE: MINIMAL QUADRATIC SYZYGIES z u y x w v

EXAMPLE: NON MINIMAL SYZYGIES z u y x w v

EXAMPLE: LINEAR SYZYGIES z u y x w v

FINAL CONSIDERATIONS • What we just said about syzygies can be made precise, both to describe local connectivity properties, as well as to define global connectivity properties of a complex • This can allow definitions of active and inactive teams within a complex, and can justify the use of these instruments to detect key components of the complex (e. g. faces that allow or accelerate diffusion across the complex) • Finally, one can use more sophisticated techniques, such as the primary decomposition of the ideals, to detect potential leadership subsets in the complex.

REFERENCES • K. Kees, L. Sparks, M. A. Mannucci, and DCS, Social Groups, Social Media, and Higher Dimensional Social Structures: Towards a Simplicial Model of Social Aggregation for Computational Communication Research, Communication Quarterly, 2013, pp. 35 -58. • K. Kee, L. Sparks, M. A. Mannucci, and DCS, Information diffusion, Facebook clusters, and the simplicial model of social aggregation: a computational simulation of simplicial diffusers for community health interventions, Health Communication 2016, pp. 385399. • A. Damiano, M. A. Mannucci, L. Sparks and DCS, Combinatorial Invariants of Social Groups: A Computational Commutative Algebra Approach, in preparation.
 God's covenant
God's covenant Difference between virtual circuit and datagram subnet
Difference between virtual circuit and datagram subnet Radius ratio
Radius ratio Inert and labile complexes
Inert and labile complexes Inert and labile complexes
Inert and labile complexes Inert and labile complexes
Inert and labile complexes Backbone networks in computer networks
Backbone networks in computer networks K complexes eeg
K complexes eeg Electra complex vs oedipus complex
Electra complex vs oedipus complex Sien fien
Sien fien Inhibitors of oxidative phosphorylation
Inhibitors of oxidative phosphorylation Site:slidetodoc.com
Site:slidetodoc.com Lanthanides have poor tendency to form complexes
Lanthanides have poor tendency to form complexes La roda maquina simple
La roda maquina simple Exemples de phrases complexes
Exemples de phrases complexes Co(gly)3
Co(gly)3 Spherical complexes of emulsified fats are known as
Spherical complexes of emulsified fats are known as Racah parameter
Racah parameter In chromatography
In chromatography Potential energy diagram
Potential energy diagram Texas industrialized housing and buildings program
Texas industrialized housing and buildings program