Lecture 5 Triangulations simplicial complexes and cell complexes




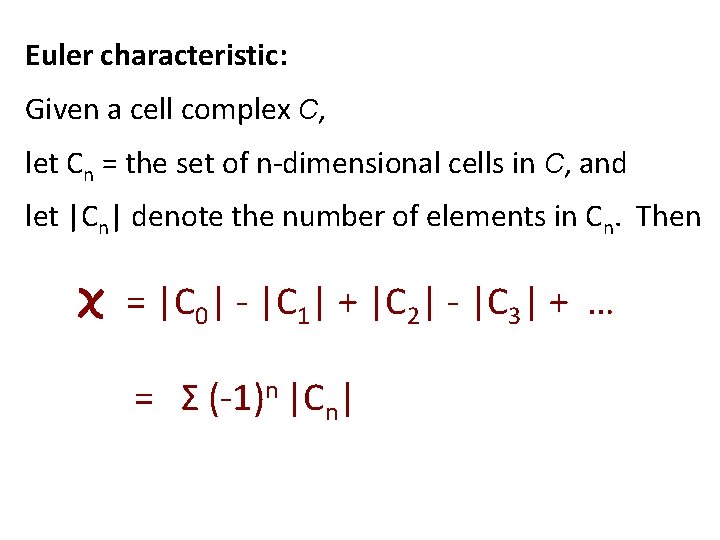

- Slides: 57

Lecture 5: Triangulations & simplicial complexes (and cell complexes). in a series of preparatory lectures for the Fall 2013 online course MATH: 7450 (22 M: 305) Topics in Topology: Scientific and Engineering Applications of Algebraic Topology Target Audience: Anyone interested in topological data analysis including graduate students, faculty, industrial researchers in bioinformatics, biology, business, computer science, cosmology, engineering, imaging, mathematics, neurology, physics, statistics, etc. Isabel K. Darcy Mathematics Department/Applied Mathematical & Computational Sciences University of Iowa http: //www. math. uiowa. edu/~idarcy/Applied. Topology. html

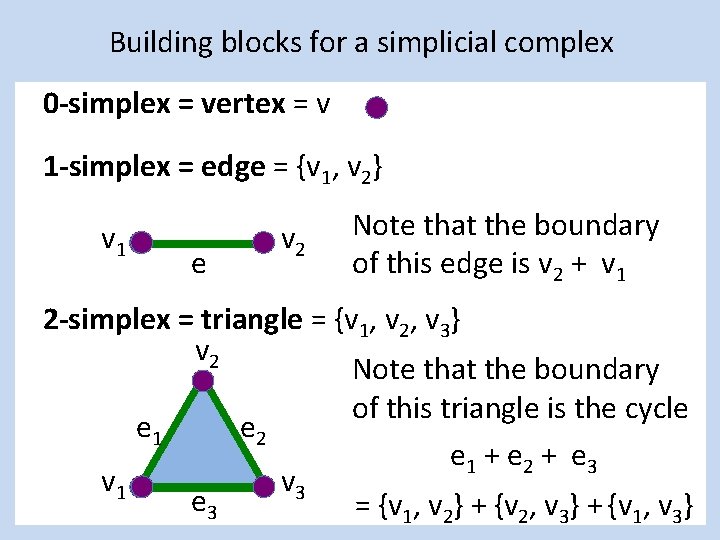
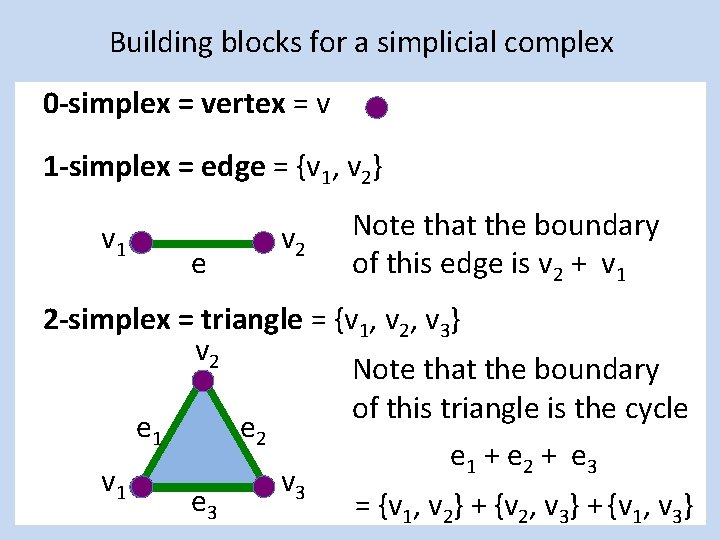
Building blocks for a simplicial complex 0 -simplex = vertex = v 1 -simplex = edge = {v 1, v 2} v 1 e v 2 Note that the boundary of this edge is v 2 + v 1 2 -simplex = triangle = {v 1, v 2, v 3} v 2 Note that the boundary of this triangle is the cycle e 1 e 2 e 1 + e 2 + e 3 v 1 v 3 e 3 = {v 1, v 2} + {v 2, v 3} + {v 1, v 3}

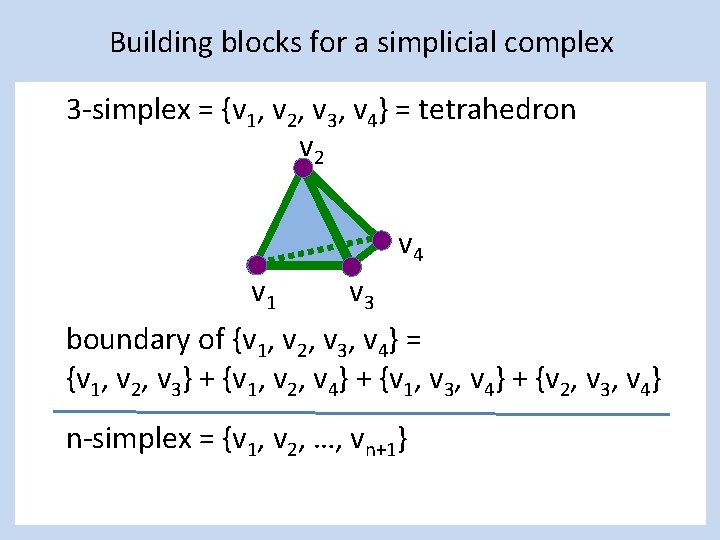
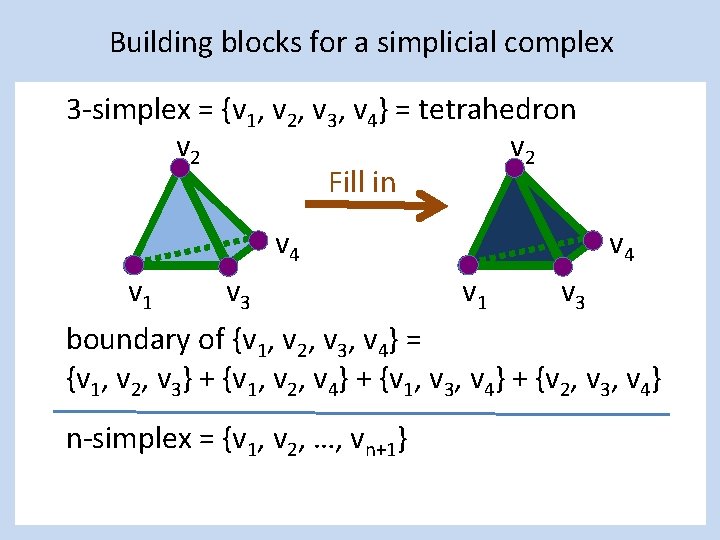
Building blocks for a simplicial complex 3 -simplex = {v 1, v 2, v 3, v 4} = tetrahedron v 2 v 4 v 1 v 3 boundary of {v 1, v 2, v 3, v 4} = {v 1, v 2, v 3} + {v 1, v 2, v 4} + {v 1, v 3, v 4} + {v 2, v 3, v 4} n-simplex = {v 1, v 2, …, vn+1}

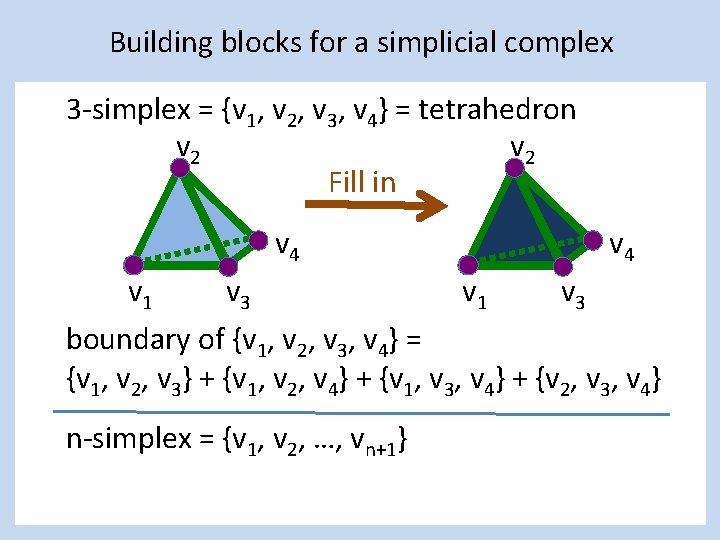
Building blocks for a simplicial complex 3 -simplex = {v 1, v 2, v 3, v 4} = tetrahedron v 2 Fill in v 4 v 1 v 3 boundary of {v 1, v 2, v 3, v 4} = {v 1, v 2, v 3} + {v 1, v 2, v 4} + {v 1, v 3, v 4} + {v 2, v 3, v 4} n-simplex = {v 1, v 2, …, vn+1}

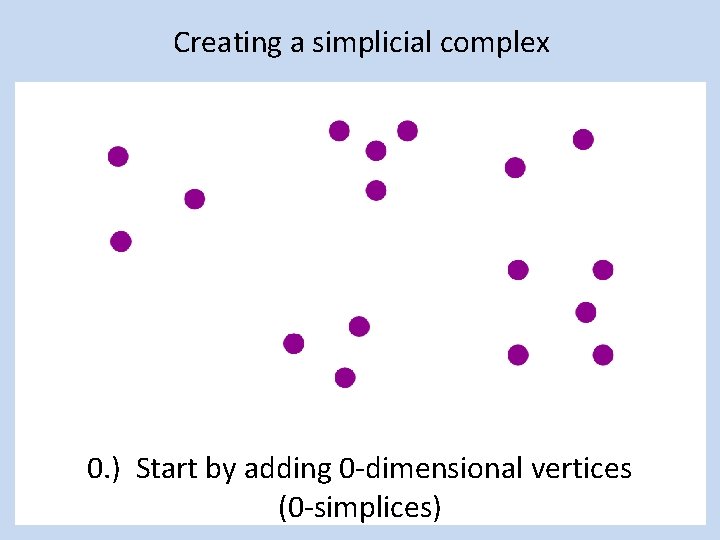
Creating a simplicial complex 0. ) Start by adding 0 -dimensional vertices (0 -simplices)

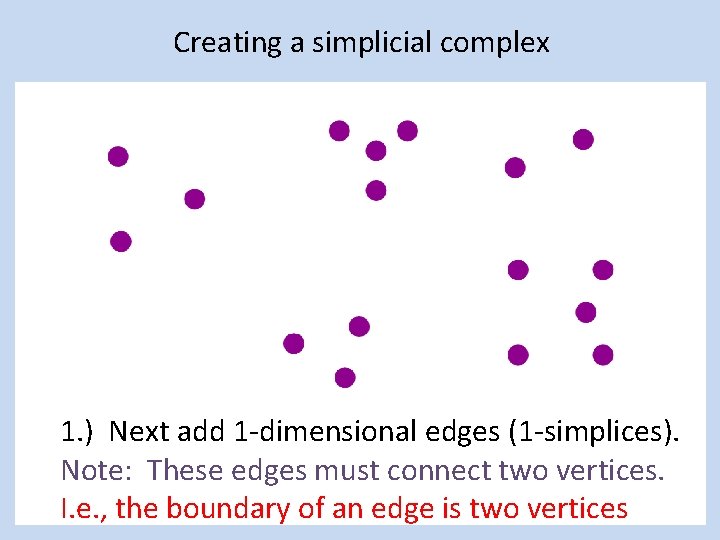
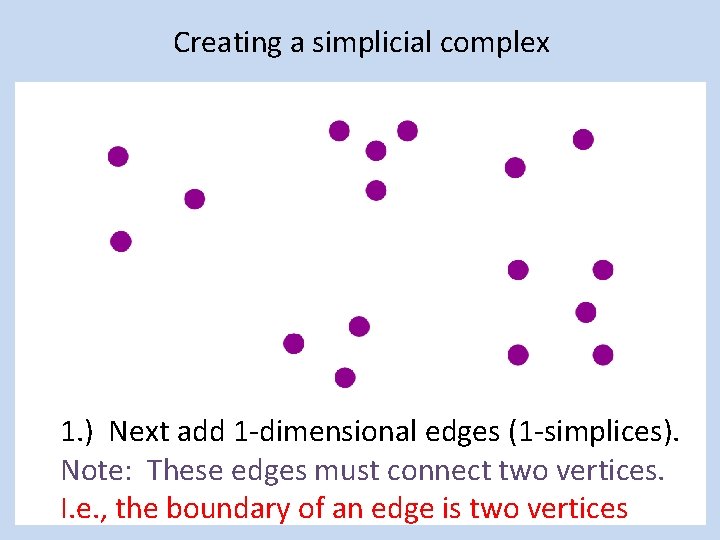
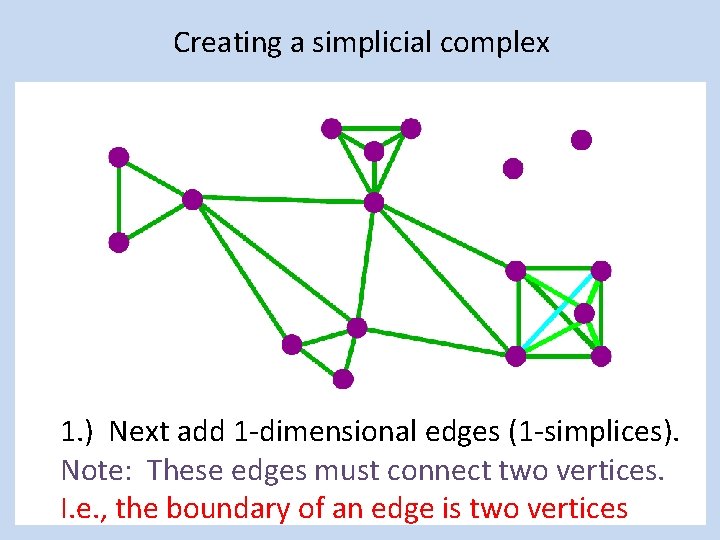
Creating a simplicial complex 1. ) Next add 1 -dimensional edges (1 -simplices). Note: These edges must connect two vertices. I. e. , the boundary of an edge is two vertices

Creating a simplicial complex 1. ) Next add 1 -dimensional edges (1 -simplices). Note: These edges must connect two vertices. I. e. , the boundary of an edge is two vertices

Creating a simplicial complex 1. ) Next add 1 -dimensional edges (1 -simplices). Note: These edges must connect two vertices. I. e. , the boundary of an edge is two vertices

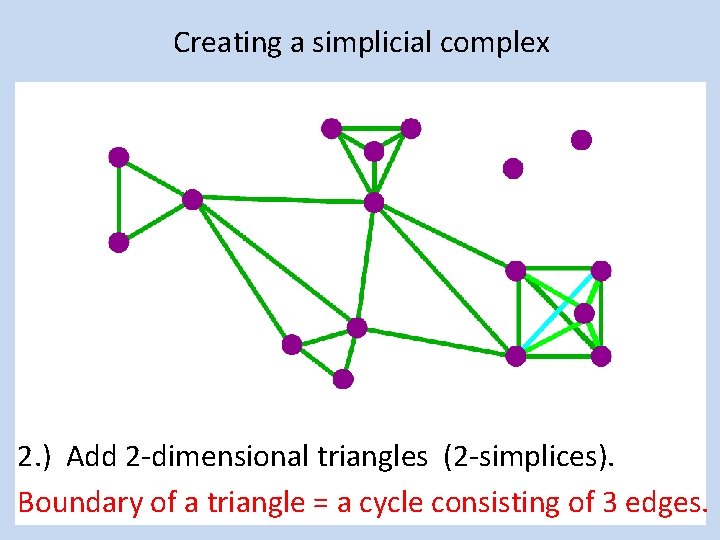
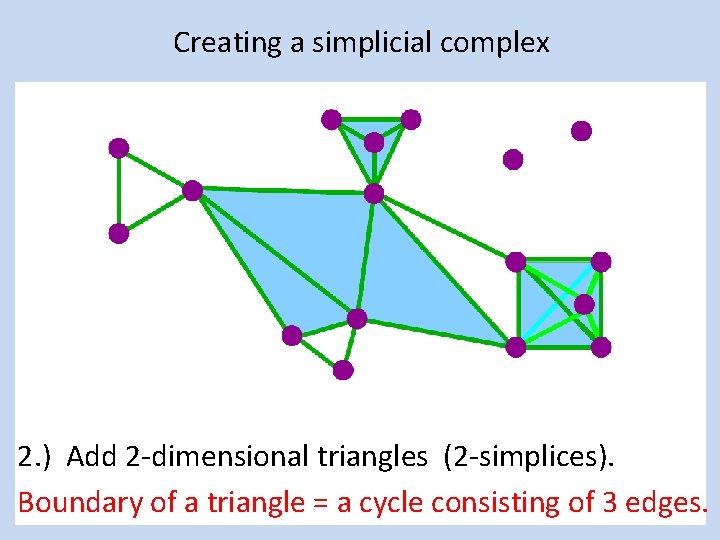
Creating a simplicial complex 2. ) Add 2 -dimensional triangles (2 -simplices). Boundary of a triangle = a cycle consisting of 3 edges.

Creating a simplicial complex 2. ) Add 2 -dimensional triangles (2 -simplices). Boundary of a triangle = a cycle consisting of 3 edges.

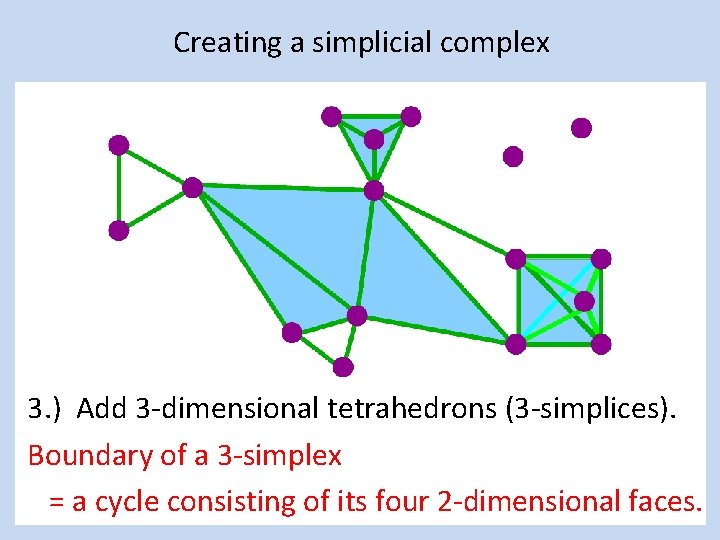
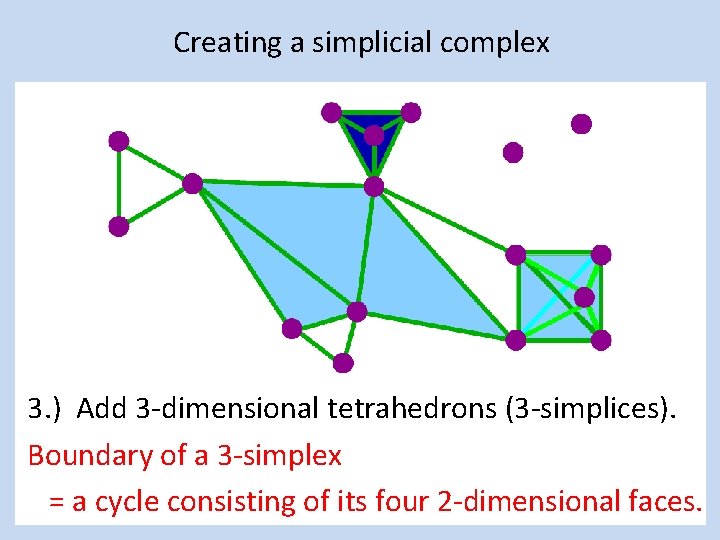
Creating a simplicial complex 3. ) Add 3 -dimensional tetrahedrons (3 -simplices). Boundary of a 3 -simplex = a cycle consisting of its four 2 -dimensional faces.

Creating a simplicial complex 3. ) Add 3 -dimensional tetrahedrons (3 -simplices). Boundary of a 3 -simplex = a cycle consisting of its four 2 -dimensional faces.

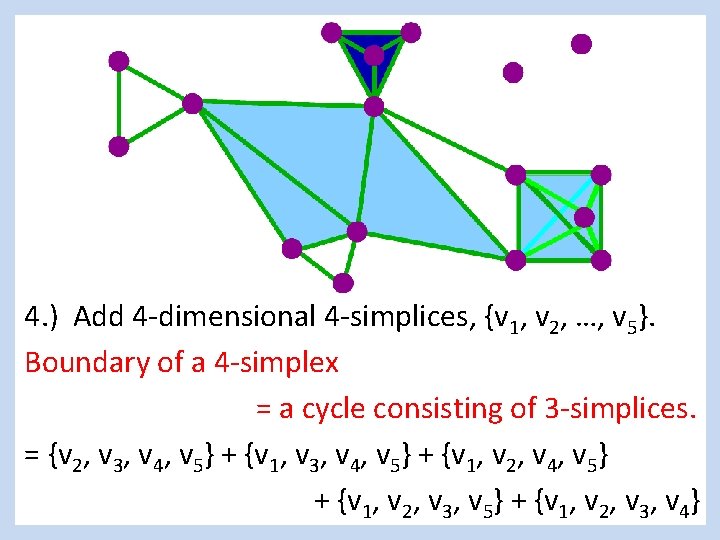
4. ) Add 4 -dimensional 4 -simplices, {v 1, v 2, …, v 5}. Boundary of a 4 -simplex = a cycle consisting of 3 -simplices. = {v 2, v 3, v 4, v 5} + {v 1, v 2, v 3, v 4}

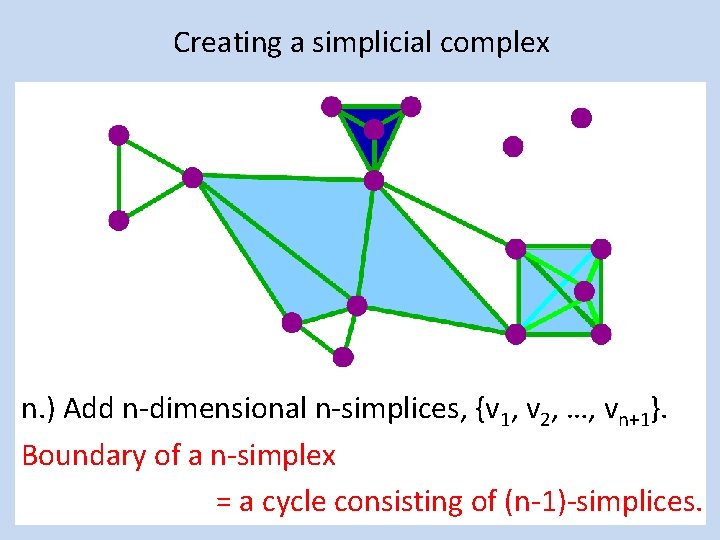
Creating a simplicial complex n. ) Add n-dimensional n-simplices, {v 1, v 2, …, vn+1}. Boundary of a n-simplex = a cycle consisting of (n-1)-simplices.

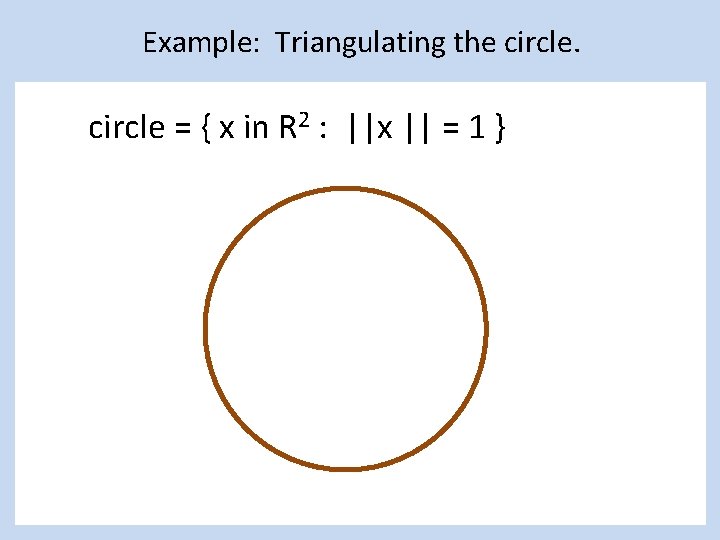
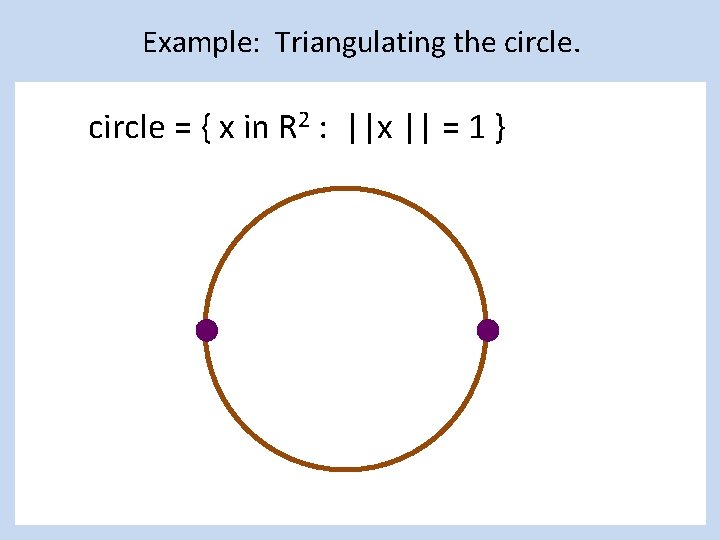
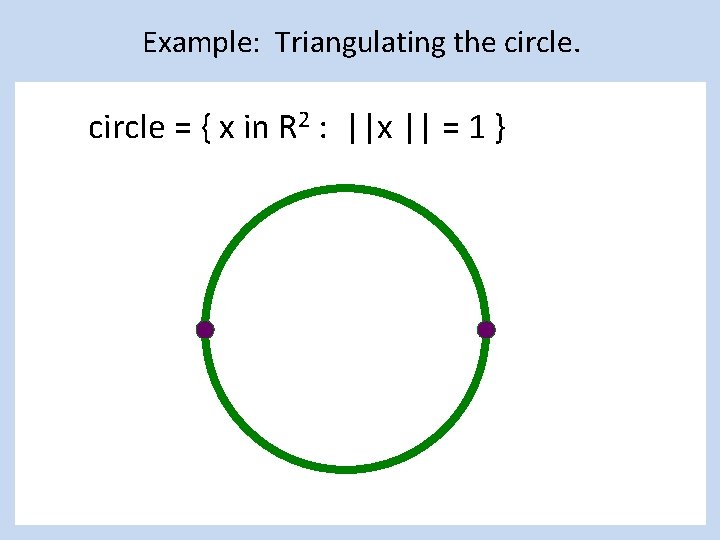
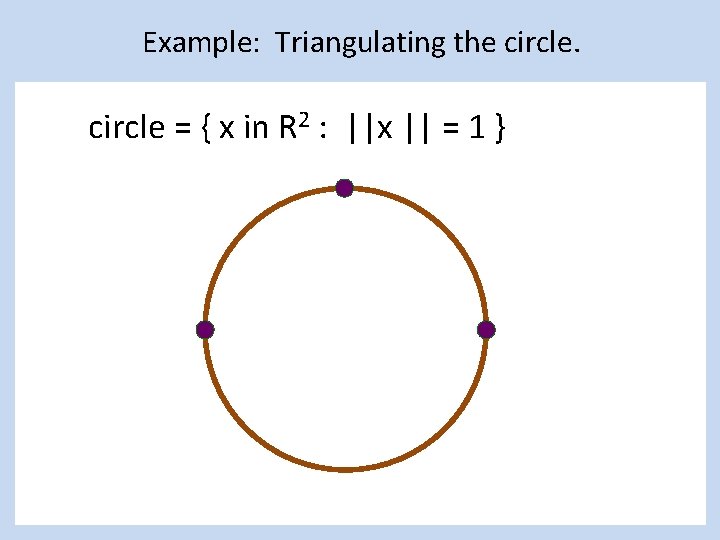
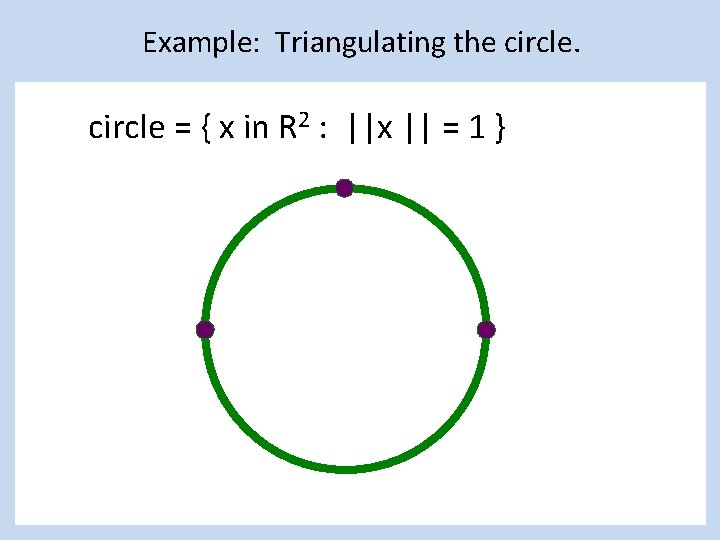
Example: Triangulating the circle = { x in R 2 : ||x || = 1 }

Example: Triangulating the circle = { x in R 2 : ||x || = 1 }

Example: Triangulating the circle = { x in R 2 : ||x || = 1 }

Example: Triangulating the circle = { x in R 2 : ||x || = 1 }

Example: Triangulating the circle = { x in R 2 : ||x || = 1 }

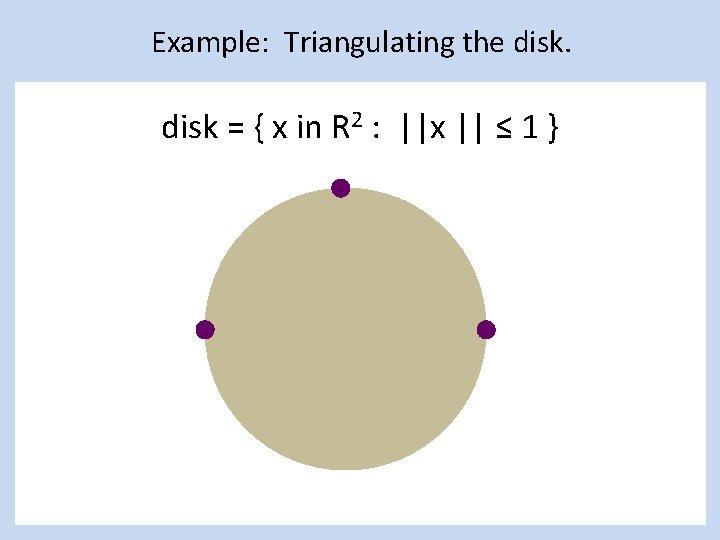
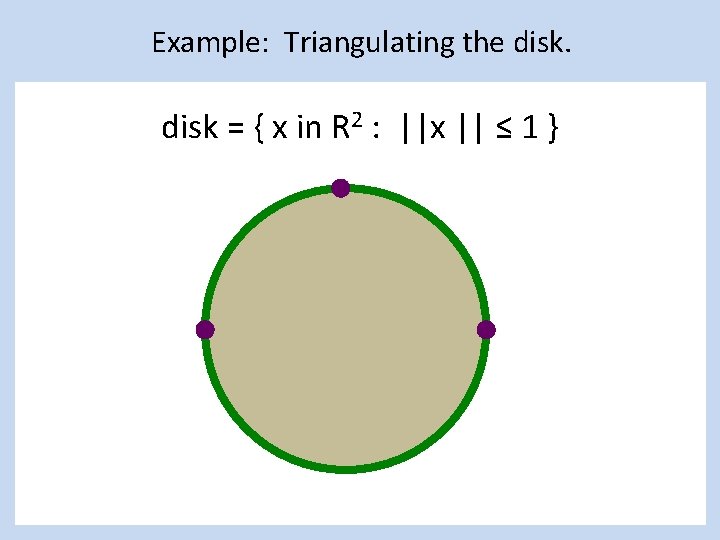
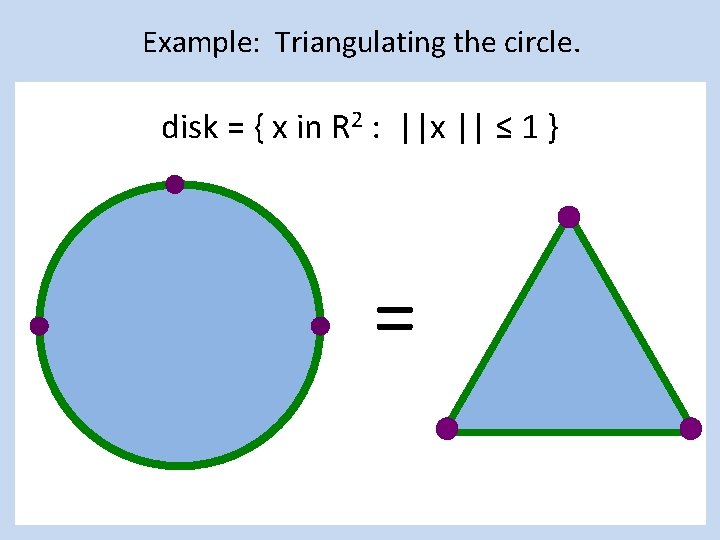
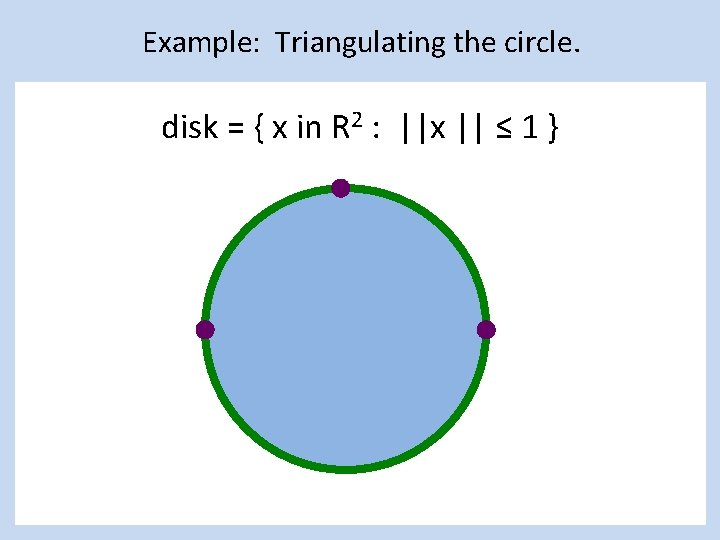
Example: Triangulating the disk = { x in R 2 : ||x || ≤ 1 }

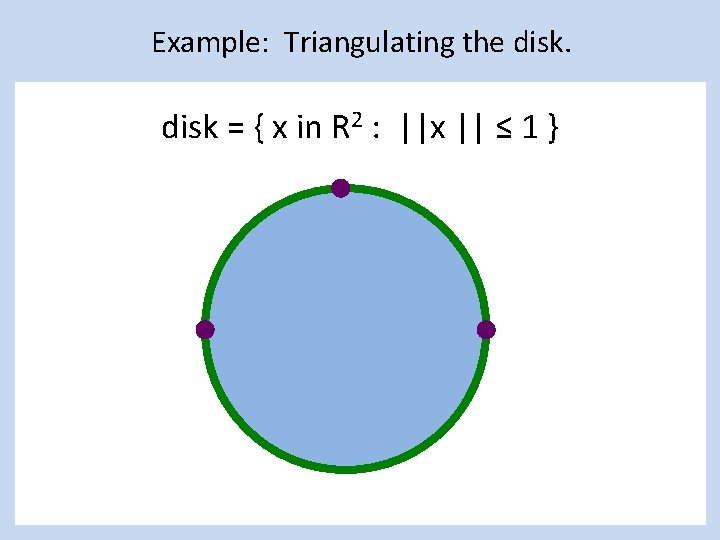
Example: Triangulating the disk = { x in R 2 : ||x || ≤ 1 }

Example: Triangulating the disk = { x in R 2 : ||x || ≤ 1 }

Example: Triangulating the disk = { x in R 2 : ||x || ≤ 1 }

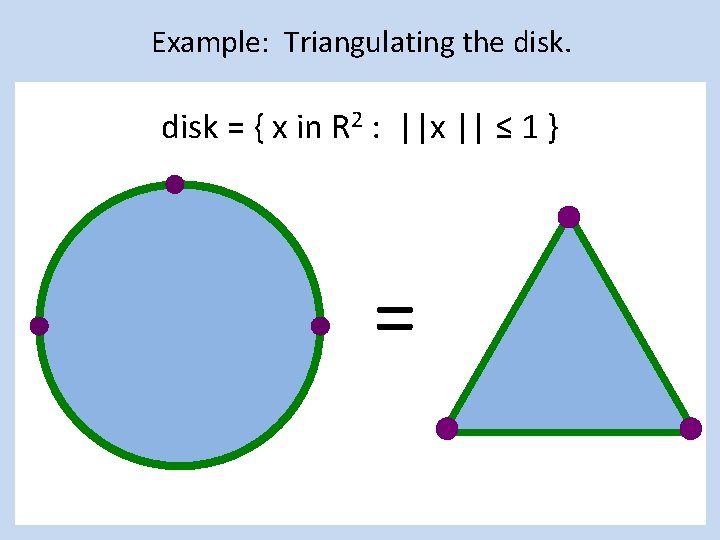
Example: Triangulating the disk = { x in R 2 : ||x || ≤ 1 } =

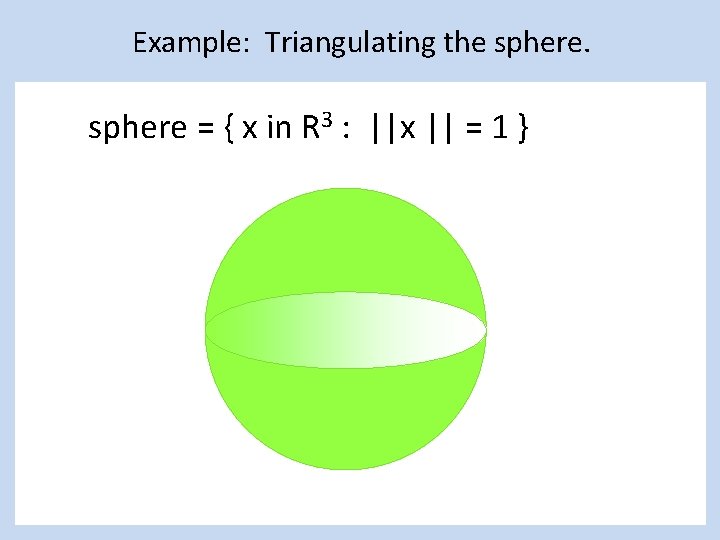
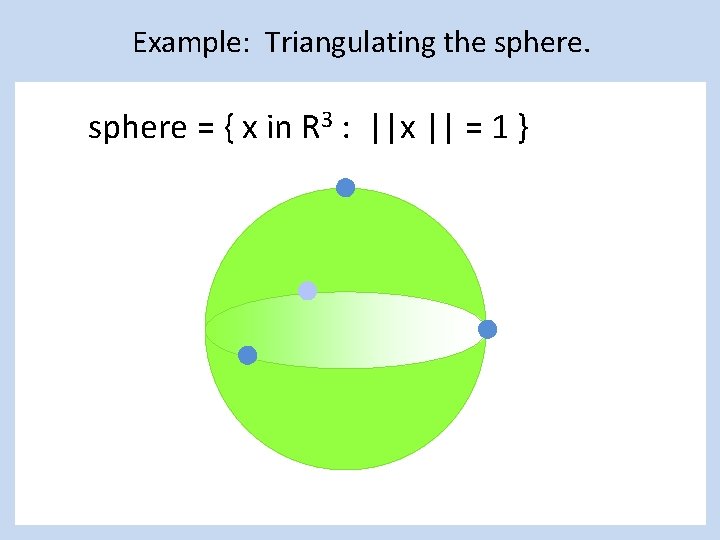
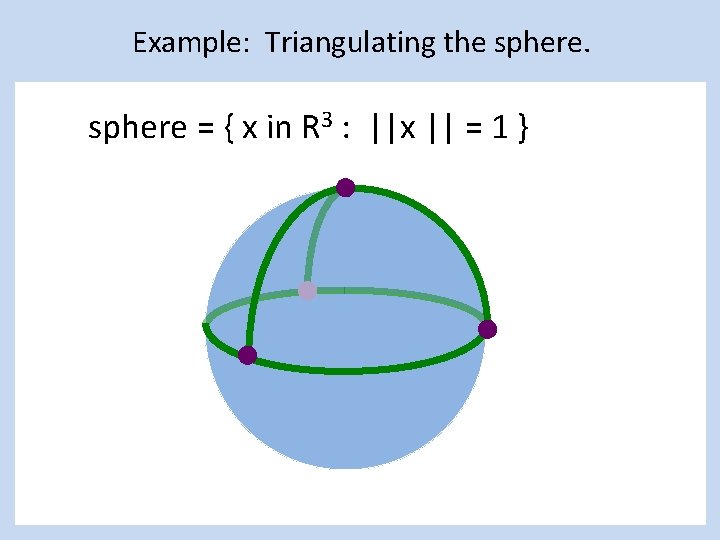
Example: Triangulating the sphere = { x in R 3 : ||x || = 1 }

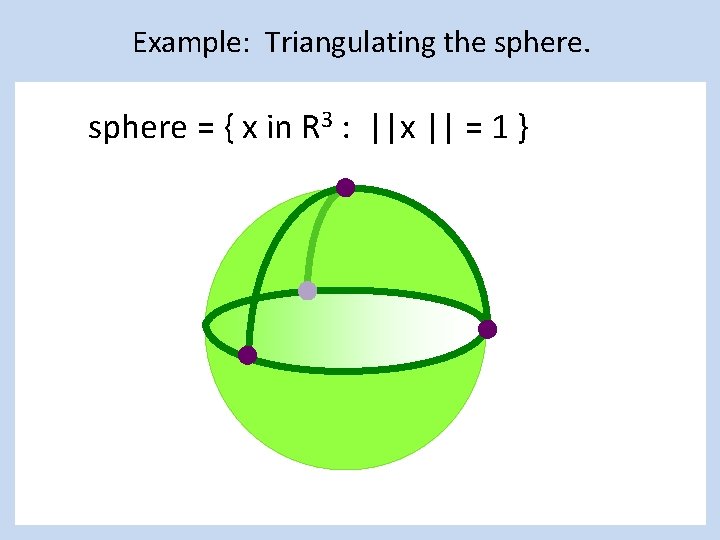
Example: Triangulating the sphere = { x in R 3 : ||x || = 1 }

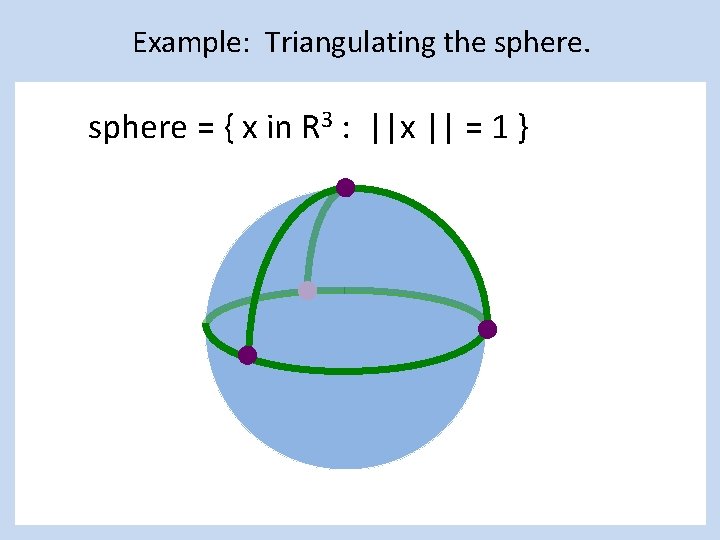
Example: Triangulating the sphere = { x in R 3 : ||x || = 1 }

Example: Triangulating the sphere = { x in R 3 : ||x || = 1 }

Example: Triangulating the circle. disk = { x in R 2 : ||x || ≤ 1 } =

Example: Triangulating the circle. disk = { x in R 2 : ||x || ≤ 1 }

Example: Triangulating the circle. disk = { x in R 2 : ||x || ≤ 1 } Fist image from http: //openclipart. org/detail/1000/a-raised-fist-by-liftarn

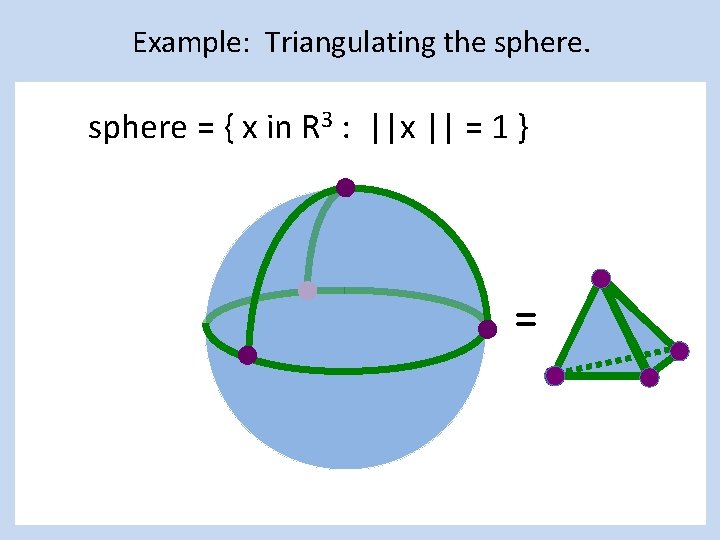
Example: Triangulating the sphere = { x in R 3 : ||x || = 1 }

Example: Triangulating the sphere = { x in R 3 : ||x || = 1 } =

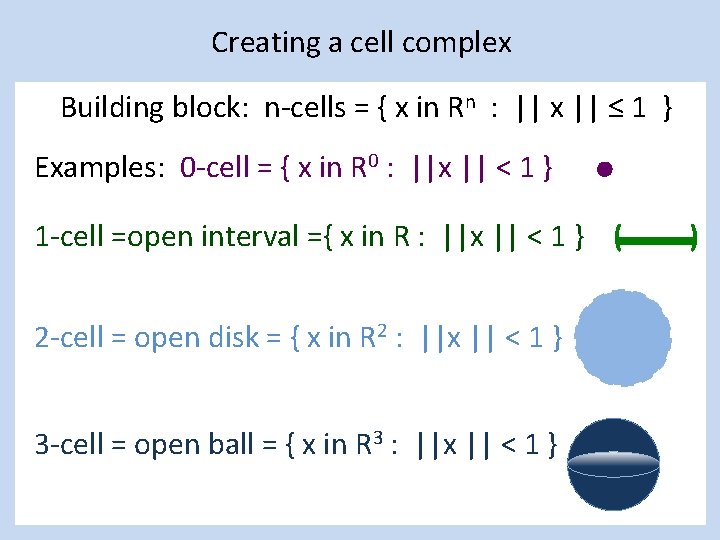
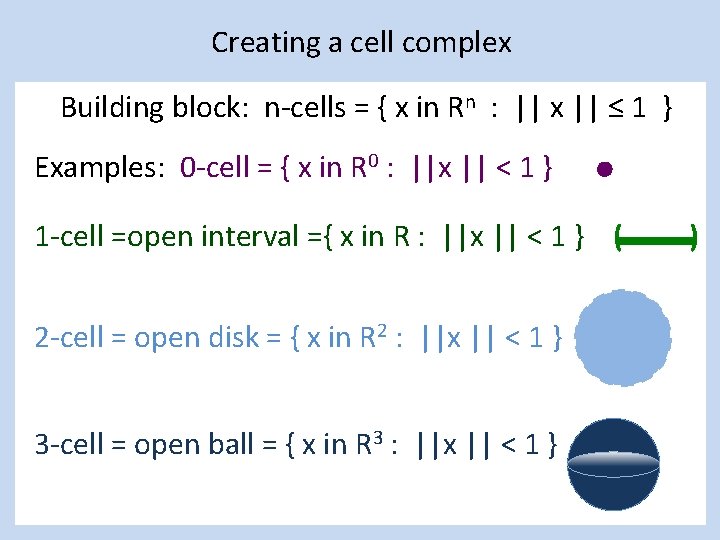
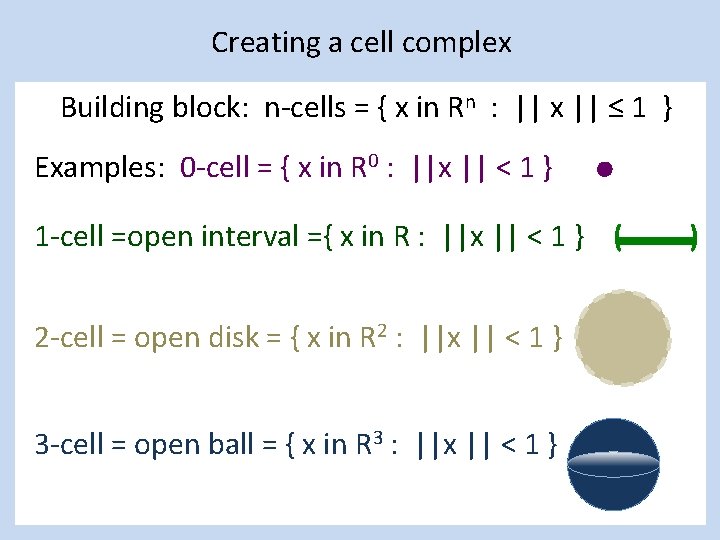
Creating a cell complex Building block: n-cells = { x in Rn : || x || ≤ 1 } Examples: 0 -cell = { x in R 0 : ||x || < 1 } 1 -cell =open interval ={ x in R : ||x || < 1 } ( 2 -cell = open disk = { x in R 2 : ||x || < 1 } 3 -cell = open ball = { x in R 3 : ||x || < 1 } )

Building blocks for a simplicial complex 0 -simplex = vertex = v 1 -simplex = edge = {v 1, v 2} v 1 e v 2 Note that the boundary of this edge is v 2 + v 1 2 -simplex = triangle = {v 1, v 2, v 3} v 2 Note that the boundary of this triangle is the cycle e 1 e 2 e 1 + e 2 + e 3 v 1 v 3 e 3 = {v 1, v 2} + {v 2, v 3} + {v 1, v 3}

Building blocks for a simplicial complex 3 -simplex = {v 1, v 2, v 3, v 4} = tetrahedron v 2 Fill in v 4 v 1 v 3 boundary of {v 1, v 2, v 3, v 4} = {v 1, v 2, v 3} + {v 1, v 2, v 4} + {v 1, v 3, v 4} + {v 2, v 3, v 4} n-simplex = {v 1, v 2, …, vn+1}

Creating a cell complex Building block: n-cells = { x in Rn : || x || ≤ 1 } Examples: 0 -cell = { x in R 0 : ||x || < 1 } 1 -cell =open interval ={ x in R : ||x || < 1 } ( 2 -cell = open disk = { x in R 2 : ||x || < 1 } 3 -cell = open ball = { x in R 3 : ||x || < 1 } )

Creating a cell complex Building block: n-cells = { x in Rn : || x || ≤ 1 } Examples: 0 -cell = { x in R 0 : ||x || < 1 } 1 -cell =open interval ={ x in R : ||x || < 1 } ( 2 -cell = open disk = { x in R 2 : ||x || < 1 } 3 -cell = open ball = { x in R 3 : ||x || < 1 } )

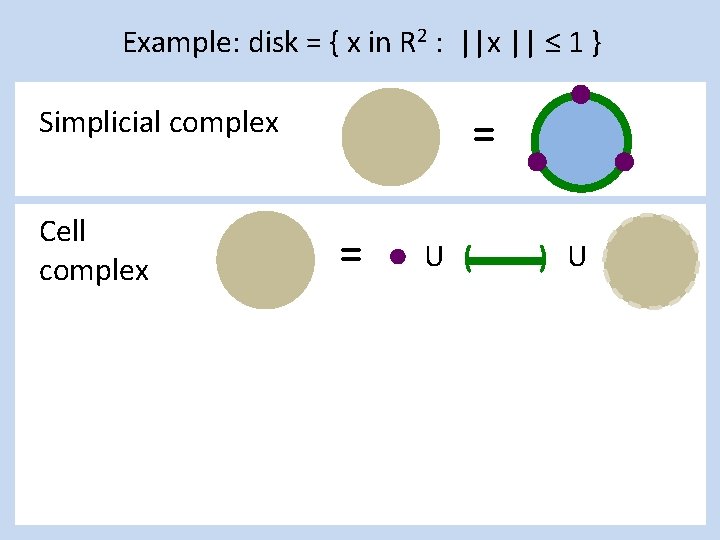
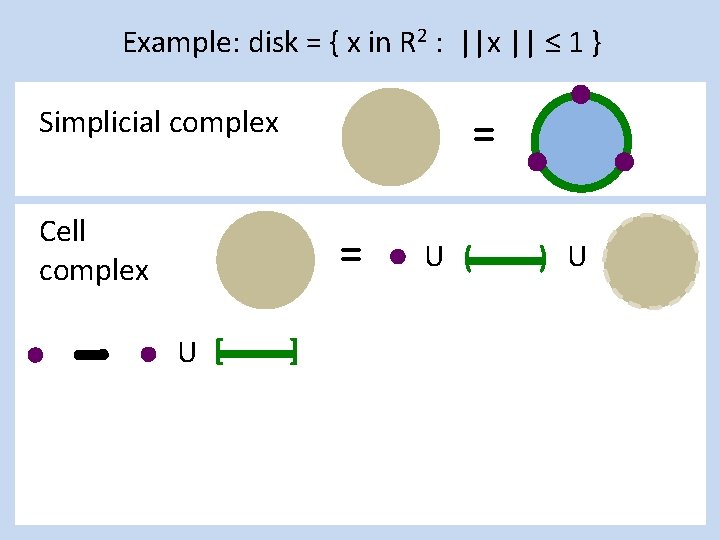
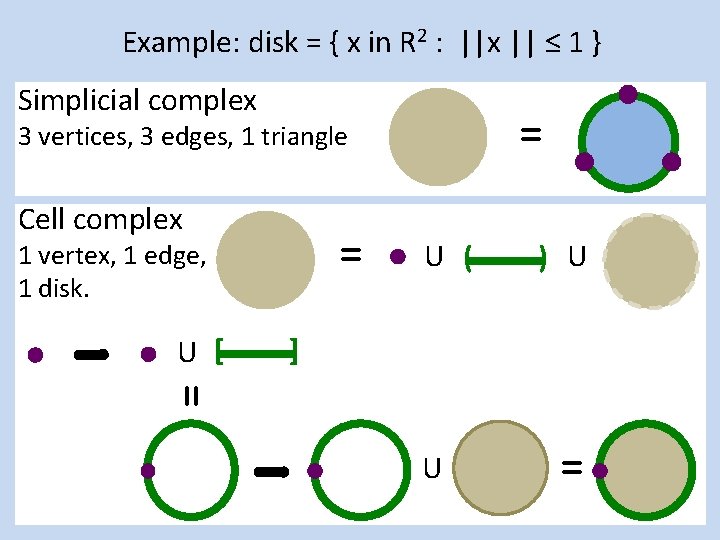
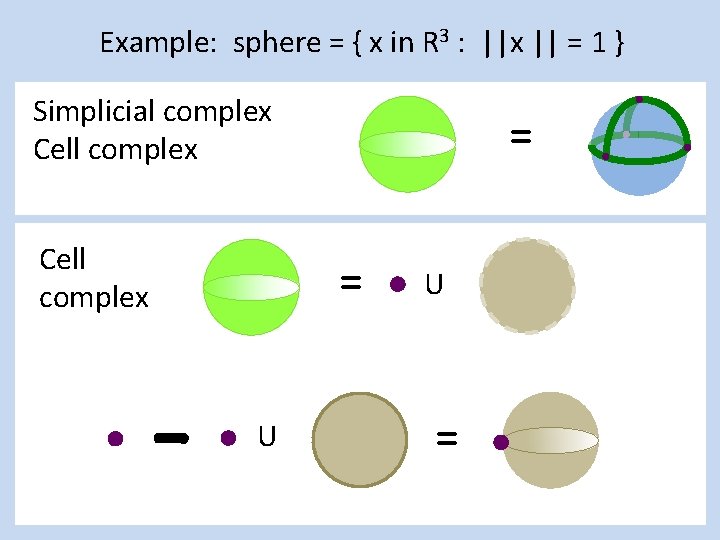
Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex Cell complex = = U ( ) U

Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex Cell complex = = U ( ) U

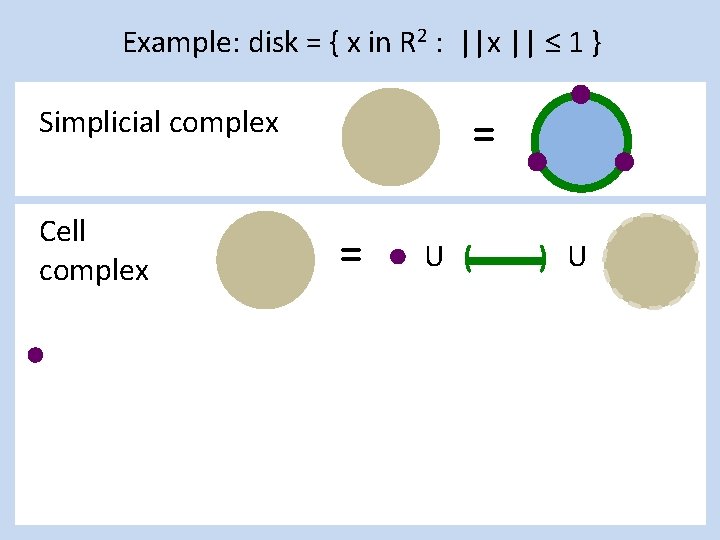
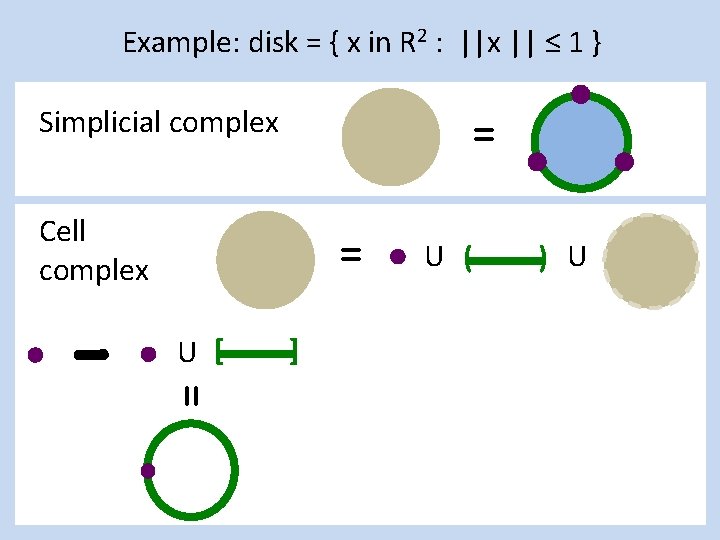
Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex = Cell complex = U ( ) U

Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex = Cell complex = U [ ] U ( ) U

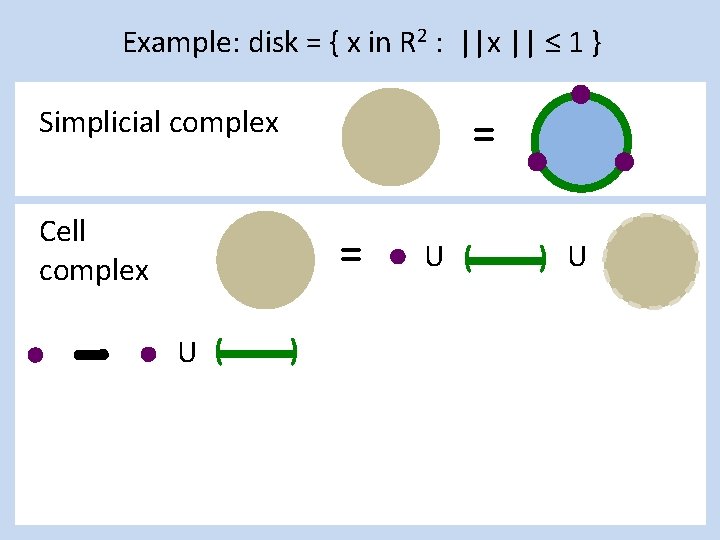
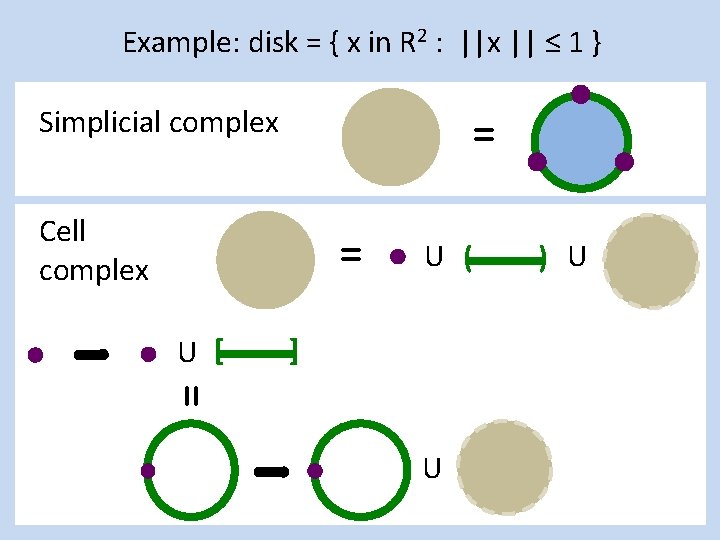
Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex = Cell complex = U [ ] U ( ) U =

Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex = Cell complex = U [ U ( ] = U ) U

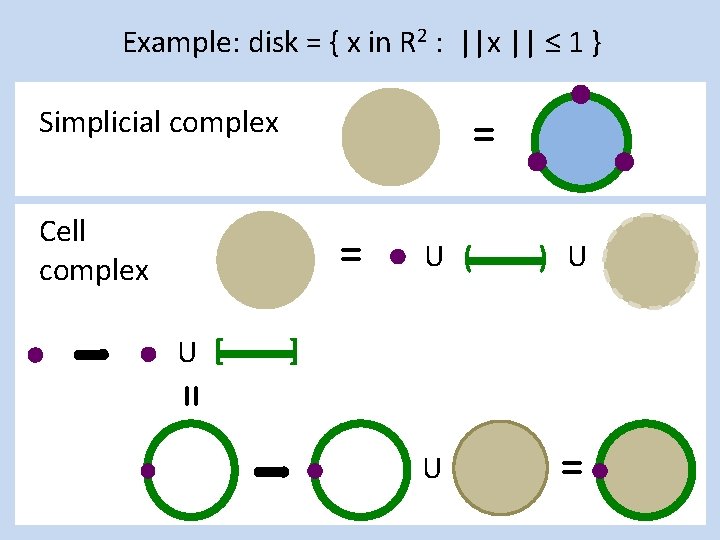
Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex = Cell complex = U [ U ( ) U ] = U =

Euler characteristic (simple form): = number of vertices – number of edges + number of faces Or in short-hand, = |V| - |E| + |F| where V = set of vertices E = set of edges F = set of 2 -dimensional faces & the notation |X| = the number of elements in the set X.

Example: disk = { x in R 2 : ||x || ≤ 1 } Simplicial complex = 3 vertices, 3 edges, 1 triangle Cell complex = 1 vertex, 1 edge, 1 disk. U [ U ( ) U ] = U =

Euler characteristic: Given a simplicial complex C, let Cn = the set of n-dimensional simplices in C, and let |Cn| denote the number of elements in Cn. Then = |C 0| - |C 1| + |C 2| - |C 3| + … = Σ (-1)n |Cn|
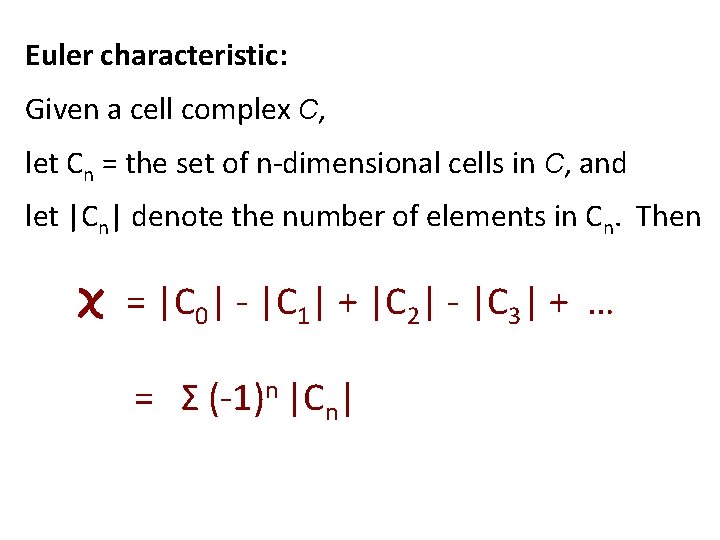
Euler characteristic: Given a cell complex C, let Cn = the set of n-dimensional cells in C, and let |Cn| denote the number of elements in Cn. Then = |C 0| - |C 1| + |C 2| - |C 3| + … = Σ (-1)n |Cn|

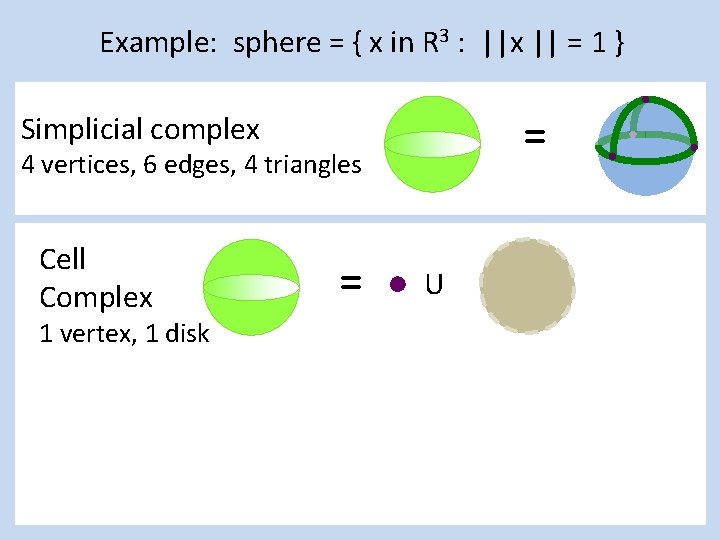
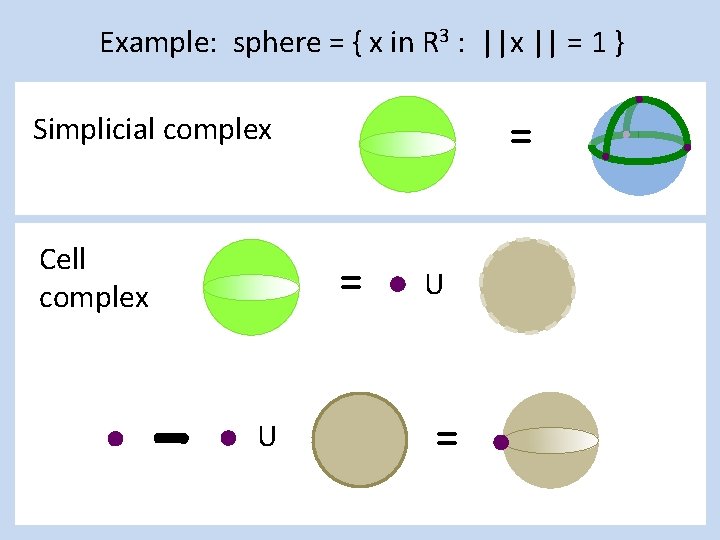
Example: sphere = { x in R 3 : ||x || = 1 } = Simplicial complex 4 vertices, 6 edges, 4 triangles Cell Complex 1 vertex, 1 disk = U

Example: sphere = { x in R 3 : ||x || = 1 } = Simplicial complex Cell complex = U

Example: sphere = { x in R 3 : ||x || = 1 } = Simplicial complex Cell complex = U U

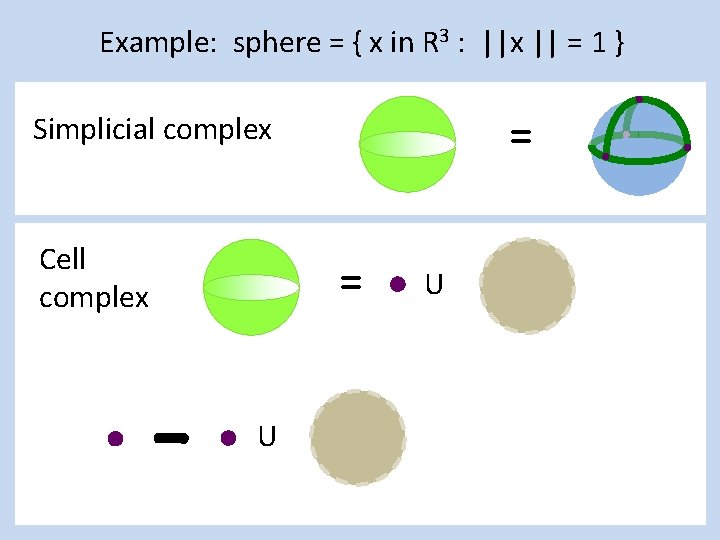
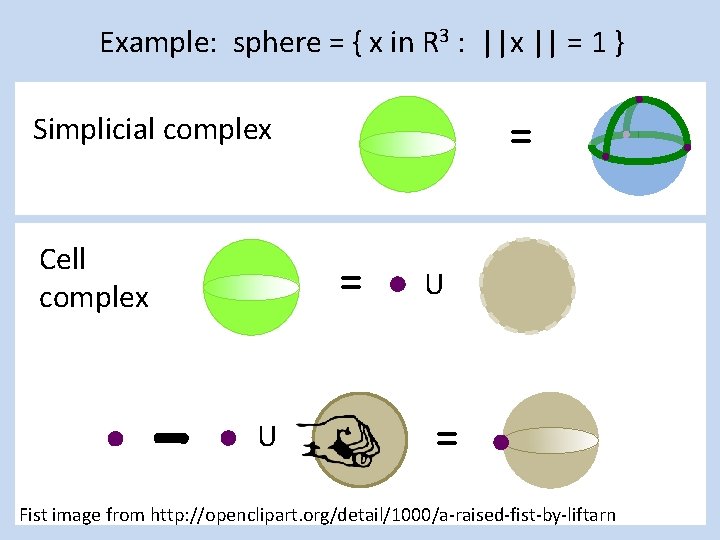
Example: sphere = { x in R 3 : ||x || = 1 } = Simplicial complex Cell complex = U U =

Example: sphere = { x in R 3 : ||x || = 1 } = Simplicial complex Cell complex = U U = Fist image from http: //openclipart. org/detail/1000/a-raised-fist-by-liftarn

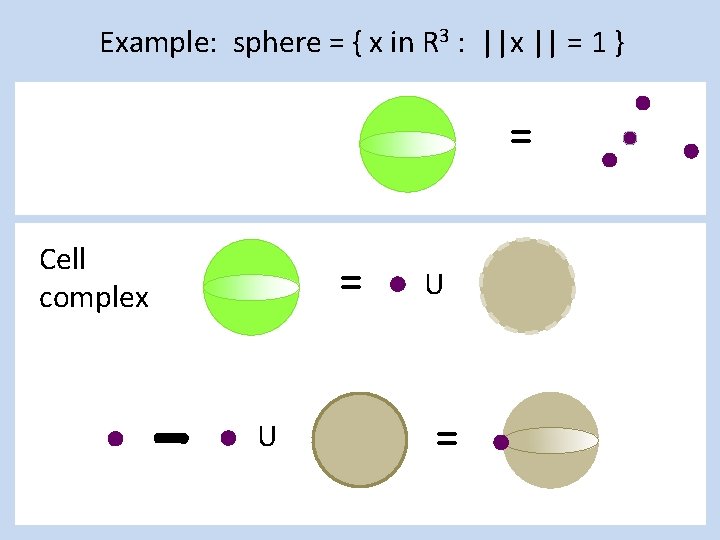
Example: sphere = { x in R 3 : ||x || = 1 } = Cell complex = U U =

Example: sphere = { x in R 3 : ||x || = 1 } = Cell complex = U U =

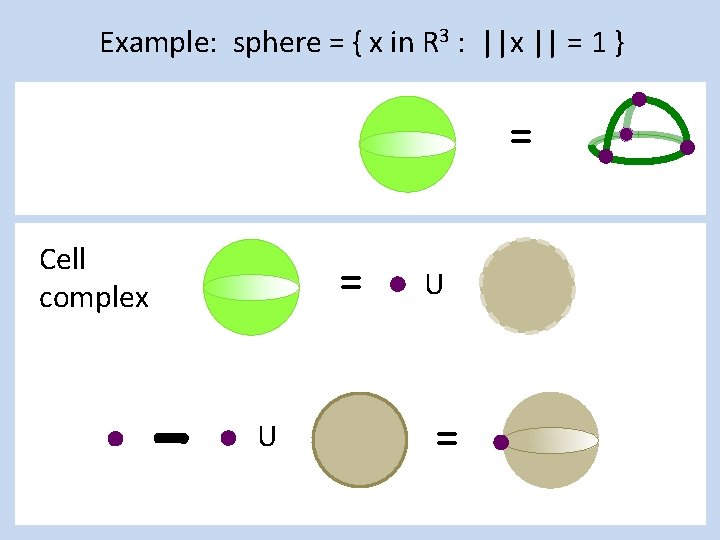
Example: sphere = { x in R 3 : ||x || = 1 } Simplicial complex Cell complex = = U U =
 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Mond process
Mond process Inert and labile complexes
Inert and labile complexes Inert and labile complexes
Inert and labile complexes Ligand spectrochemical series
Ligand spectrochemical series Fibroblast
Fibroblast Cleavage
Cleavage Eeg eye
Eeg eye The electra complex
The electra complex Chion lion
Chion lion Uncouplers of oxidative phosphorylation
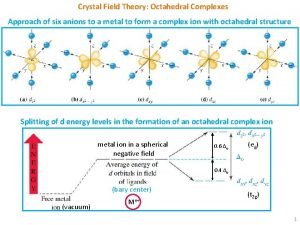
Uncouplers of oxidative phosphorylation Crystal field theory for tetrahedral complexes
Crystal field theory for tetrahedral complexes Actinide contraction
Actinide contraction La roda maquina simple
La roda maquina simple Exemples des phrases complexes
Exemples des phrases complexes Optical isomers of octahedral complexes
Optical isomers of octahedral complexes Spherical complexes of emulsified fats are known as
Spherical complexes of emulsified fats are known as Racah parameter
Racah parameter Orgel diagram is used for
Orgel diagram is used for Potential energy diagram labeled
Potential energy diagram labeled Man camps in texas
Man camps in texas A ________ is formed from beadlike histone-dna complexes.
A ________ is formed from beadlike histone-dna complexes. Advantages of diaphragm cell
Advantages of diaphragm cell Linear chromosomes in eukaryotes
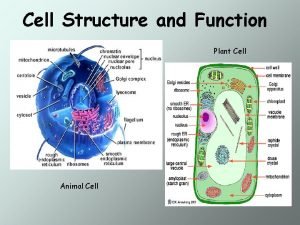
Linear chromosomes in eukaryotes Venn diagram plant and animal cell
Venn diagram plant and animal cell Plant cell structure
Plant cell structure What is the structure and function of the smooth er?
What is the structure and function of the smooth er? Lead acid battery primary or secondary
Lead acid battery primary or secondary Differences between plant animal and bacterial cells
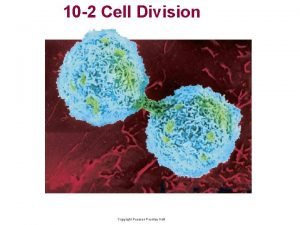
Differences between plant animal and bacterial cells Section 10-2 cell division
Section 10-2 cell division Life
Life The scientist mathias schleiden studied _______ in ______.
The scientist mathias schleiden studied _______ in ______. Idealized plant cell
Idealized plant cell Walker cell and hadley cell
Walker cell and hadley cell Cell cycle and cell division
Cell cycle and cell division Plant vs animal cell venn diagram
Plant vs animal cell venn diagram Cell cycle and cell division
Cell cycle and cell division Electrolysis vs voltaic cell
Electrolysis vs voltaic cell Flexible covering of an animal cell
Flexible covering of an animal cell Golgi body school analogy
Golgi body school analogy Prokaryotic cell vs eukaryotic cell
Prokaryotic cell vs eukaryotic cell The cell reaction for the zn-h2 cell is
The cell reaction for the zn-h2 cell is Dry cell vs wet cell
Dry cell vs wet cell Middle lamella
Middle lamella Carbohydrate in cell membrane
Carbohydrate in cell membrane Cell strain
Cell strain Cell line vs cell strain
Cell line vs cell strain Cell city introduction
Cell city introduction Cell-cell junction
Cell-cell junction Cell-cell junction
Cell-cell junction Which organelle prepares proteins for specific jobs
Which organelle prepares proteins for specific jobs Carbohydrate side chain
Carbohydrate side chain Cell structure graphic organizer
Cell structure graphic organizer Prokaryotic and eukaryotic cells worksheet
Prokaryotic and eukaryotic cells worksheet Biology.arizona.edu/cell bio/activities/cell cycle/01.html
Biology.arizona.edu/cell bio/activities/cell cycle/01.html Matlab
Matlab Magnetism
Magnetism Power system dynamics and stability lecture notes
Power system dynamics and stability lecture notes