PROF SSA STEFANIA SCIUTO Gli insiemi SI INDICA

PROF. SSA STEFANIA SCIUTO Gli insiemi

SI INDICA CON IL NOME INSIEME MATEMATICO OGNI RAGGRUPPAMENTO BEN DEFINITO DI OGGETTI, PERSONE, ANIMALI, NUMERI, LETTERE, . . . DISTINTI L’UNO DALL’ALTRO, TALE DA POTER DIRE CON PRECISIONE SE UN CERTO ELEMENTO APPARTENGA O NO AL RAGGRUPPAMENTO CONSIDERATO A . mi. fa . re . do. la. si. sol B . u. o. c. s . l . a . 5. 7. 3 . 8. 1 C . 2 . 0. 4. 9. 6 UN INSIEME SI INDICA CON UNA LETTERA MAIUSCOLA DELL’ALFABETO: A, B, C, . . . E OGNI SUO ELEMENTO CON UNA LETTERA MINUSCOLA: a, b, c, . . . OPPURE CON IL SUO NOME O CON IL SUO SIMBOLO

UN INSIEME È FINITO SE È CONTIENE UN NUMERO LIMITATO DI ELEMENTI. Ad esempio… LE LETTERE DELLA PAROLA «SCUOLA» I NUMERI NATURALI MINORI DI 6 GLI ALUNNI DELLA 1 B LE NOTE MUSICALI LE STAGIONI

Un insieme è INFINITO se è contiene un numero infinito di elementi. Ad esempio… I NUMERI NATURALI I NUMERI PARI LE STELLE DEL CIELO I MULTIPLI DI 7

UN INSIEME È VUOTO SE NON CONTIENE ELEMENTI; SI INDICA CON IL SIMBOLO Æ Ad esempio… I MESI DELL’ANNO CON 32 GIORNI LE SETTIMANE SENZA SABATO LE CONSONANTI DELLA PAROLA «AIA» GLI ALUNNI DELLA 1 B ALTI 190 CM

1° MODO: I DIAGRAMMI DI VENN GLI INSIEMI SI RAPPRESENTANO CON UNA LINEA CHIUSA (UN RECINTO) IN CUI METTERE GLI ELEMENTI DELL'INSIEME A B . s. u. l . o. c. a

2° MODO: RAPPRESENTAZIONE PER ELENCAZIONE QUESTO TIPO DI RAPPRESENTAZIONE CONSISTE NELL’ELENCARE, TRA DUE PARENTESI GRAFFE, TUTTI GLI ELEMENTI DELL’INSIEME CONSIDERATO, SEPARATI DA UNA VIRGOLA. A = { s, c, u, o, l, a}

3° MODO: RAPPRESENTAZIONE PER CARATTERISTICA Gli elementi dell'insieme si indicano con una proprietà che li identifica in modo preciso A = { x / x è una lettera della parola «scuola» } si legge: l'insieme A è formato da tutti gli elementi x tali che x è una lettera della parola «scuola» Questa rappresentazione si usa soprattutto quando gli elementi sono molto numerosi e sarebbe difficile e lungo elencarli tutti. Esempio: B = { b / b è un mammifero}

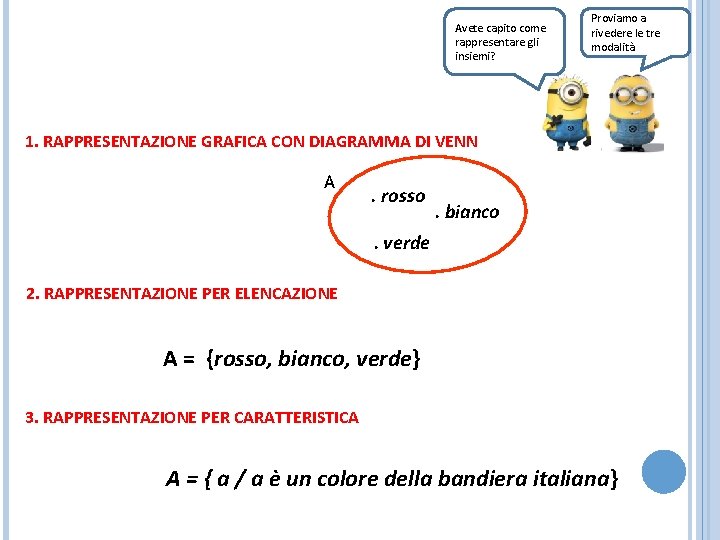
Avete capito come rappresentare gli insiemi? Proviamo a rivedere le tre modalità 1. RAPPRESENTAZIONE GRAFICA CON DIAGRAMMA DI VENN A . rosso . bianco . verde 2. RAPPRESENTAZIONE PER ELENCAZIONE A = {rosso, bianco, verde} 3. RAPPRESENTAZIONE PER CARATTERISTICA A = { a / a è un colore della bandiera italiana}

UN INSIEME B SI DICE SOTTOINSIEME PROPRIO DI UN INSIEME A SE OGNI ELEMENTO DI B APPARTIENE AD A. ESEMPIO : A = { a/a è un mese dell'anno } B = { b/b è un mese dell'anno di 30 giorni } B ⊂ A SI LEGGE: B È INCLUSO IN A

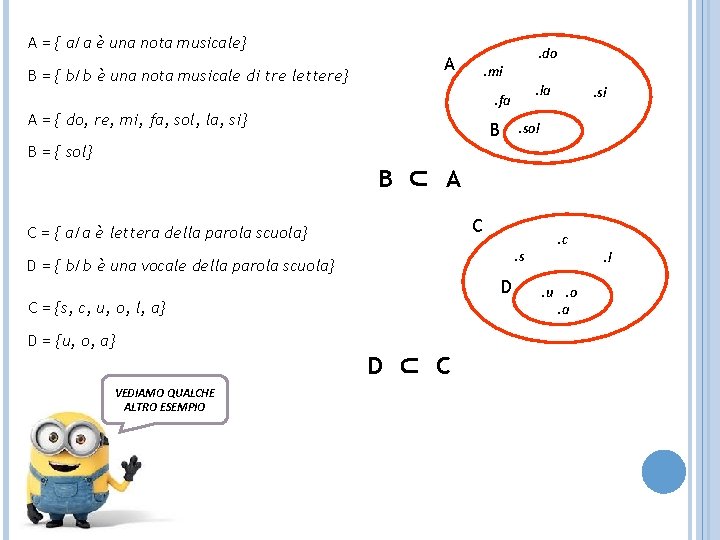
A = { a/a è una nota musicale} B = { b/b è una nota musicale di tre lettere} . do A . mi. la . fa A = { do, re, mi, fa, sol, la, si} B . si . sol B = { sol} B ⊂ A C C = { a/a è lettera della parola scuola} . s D = { b/b è una vocale della parola scuola} D C = {s, c, u, o, l, a} D = {u, o, a} D ⊂ C VEDIAMO QUALCHE ALTRO ESEMPIO . c. l. u. o. a

PROVIAMO ADESSO A CONSIDERARE L’INSIEME A FORMATO DALLE LETTERE DELLA PAROLA «ARMADILLO» E L’INSIEME B FORMATO DALLE LETTERE DELLA PAROLA «DAINO» A = { a, r, m, d, i, l, o} B = { a, d, i, n, o} OSSERVIAMO CHE B NON È UN SOTTOINSIEME DI A PERCHÉ NON TUTTI I SUOI ELEMENTI SONO COMPRESI IN A INFATTI NELLA PAROLA «DAINO» È PRESENTE LA LETTERA «n» CHE NON TROVIAMO NELLA PAROLA «ARMADILLO» PER INDICARE CHE B NON È SOTTOINSIEME DI A SI SCRIVE NEL SEGUENTE MODO: B ⊂ A SI LEGGE: B NON È INCLUSO IN A

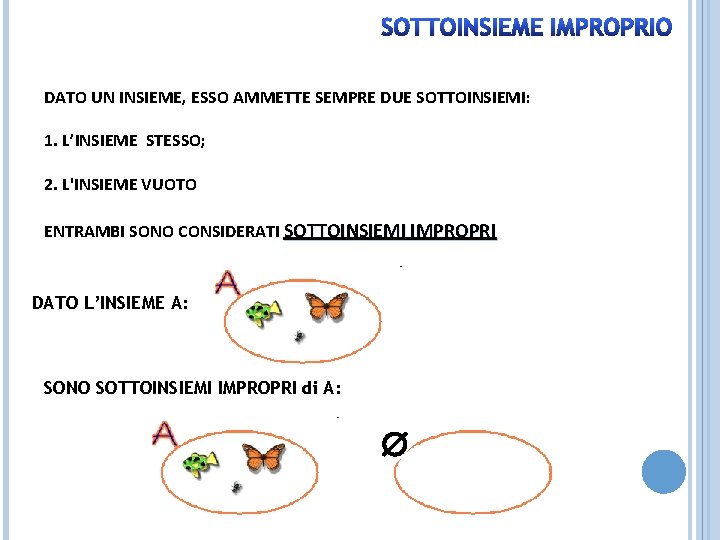
SOTTOINSIEME IMPROPRIO DATO UN INSIEME, ESSO AMMETTE SEMPRE DUE SOTTOINSIEMI: 1. L’INSIEME STESSO; 2. L'INSIEME VUOTO ENTRAMBI SONO CONSIDERATI SOTTOINSIEMI IMPROPRI DATO L’INSIEME A: SONO SOTTOINSIEMI IMPROPRI di A: Æ

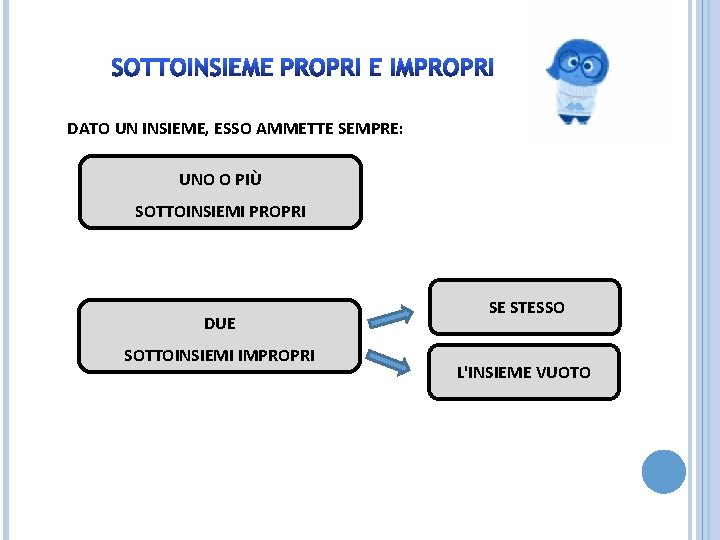
SOTTOINSIEME PROPRI E IMPROPRI DATO UN INSIEME, ESSO AMMETTE SEMPRE: UNO O PIÙ SOTTOINSIEMI PROPRI DUE SOTTOINSIEMI IMPROPRI SE STESSO L'INSIEME VUOTO

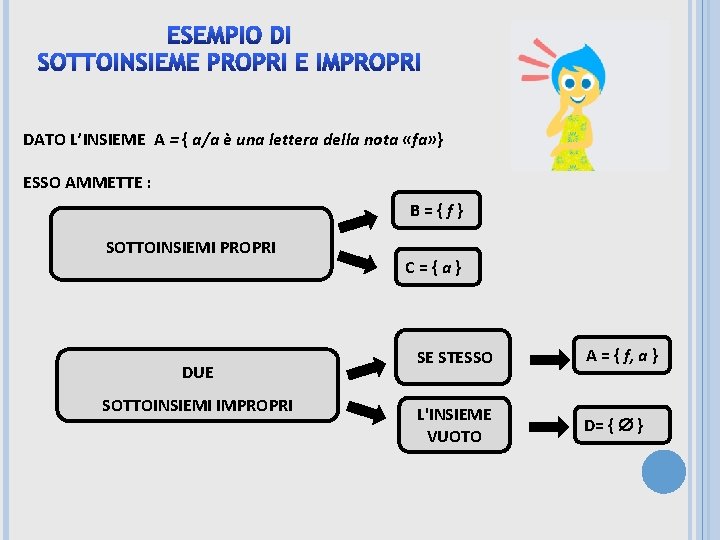
ESEMPIO DI SOTTOINSIEME PROPRI E IMPROPRI DATO L’INSIEME A = { a/a è una lettera della nota «fa» } ESSO AMMETTE : B={f} SOTTOINSIEMI PROPRI DUE SOTTOINSIEMI IMPROPRI C={a} SE STESSO A = { f, a } L'INSIEME VUOTO D= { Æ }

Insieme delle parti L'INSIEME FORMATO DA TUTTI I POSSIBILI SOTTOINSIEMI PROPRI ED IMPROPRI DI A SI CHIAMA INSIEME DELLE PARTI DI A E SI INDICA CON Ã(A). CONSIDERIAMO L’INSIEME A FORMATO DALLE PRIME TRE LETTERE DELL’ALFABETO A = {a, b, c} L'INSIEME Ã(A) SARÀ Ã(A) = {Æ; �{a; b; c}; {a}; {b}; {c}; {a; b}; {a; c}; {b; c} } N. B. i primi due sottoinsiemi sono impropri, gli altri sono propri Ã(A) A. a. b . c Æ {a} {ab} {a; c} {a; b; c} {b; c}

LA PARTIZIONE DI UN INSIEME� Consideriamo l'insieme A formato da alcune regioni italiane: A = {Piemonte; Liguria; Veneto; Toscana; Marche; Puglia; Campania; Calabria} e formiamo tre sottoinsiemi: B = {Piemonte; Liguria; Veneto} C = {Toscana; Marche} D = {Puglia; Campania; Calabria} Osserviamo le caratteristiche di questi sottoinsiemi: • Non ci sono elementi in comune tra i sottoinsiemi • Nessuno di questi sottoinsiemi è vuoto. • Riunendo i sottoinsiemi otteniamo di nuovo l'insieme di partenza A. In questo caso abbiamo fatto una partizione dell'insieme A. Operare una partizione dell'insieme significa dunque suddividerlo in due o più sottoinsiemi che devono rispettare queste condizioni: - non devono avere elementi in comune - non devono essere vuoti - riuniti tutti i sottoinsiemi, si deve ottenere l'insieme di partenza.

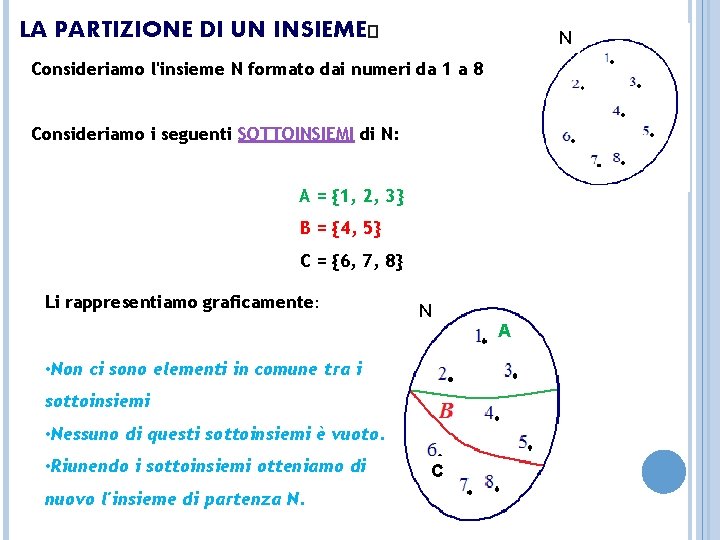
LA PARTIZIONE DI UN INSIEME� N Consideriamo l'insieme N formato dai numeri da 1 a 8 Consideriamo i seguenti SOTTOINSIEMI di N: A = {1, 2, 3} B = {4, 5} C = {6, 7, 8} Li rappresentiamo graficamente: N A • Non ci sono elementi in comune tra i sottoinsiemi • Nessuno di questi sottoinsiemi è vuoto. • Riunendo i sottoinsiemi otteniamo di nuovo l'insieme di partenza N. C

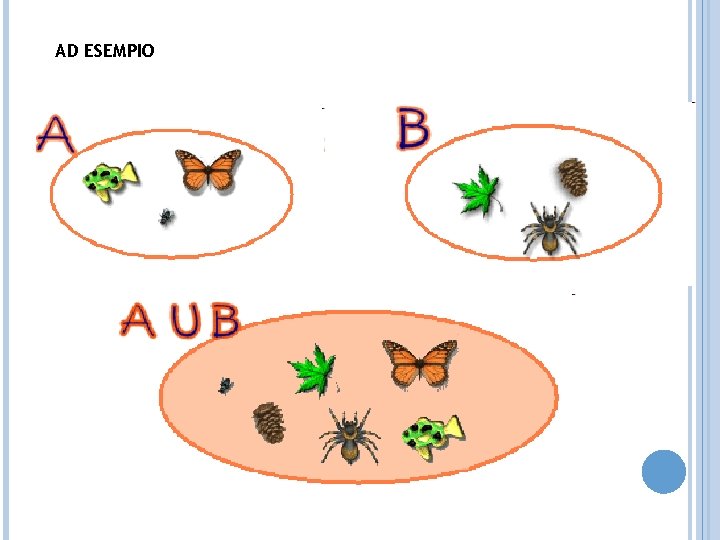
CONSIDERIAMO I SEGUENTI INSIEMI: L’INSIEME A = { a , b , c } L’INSIEME B = { c , d , e } POI CONSIDERIAMO L’INSIEME C = { a , b , c , d , e } POSSIAMO NOTARE CHE L’INSIEME C CONTIENE SIA GLI ELEMENTI DI A CHE GLI ELEMENTI DI B L’INSIEME C è L’INSIEME UNIONE DI A E B E SI INDICA: AUB={a, b, c, d, e} CHE SI LEGGE A UNITO CON B

AD ESEMPIO

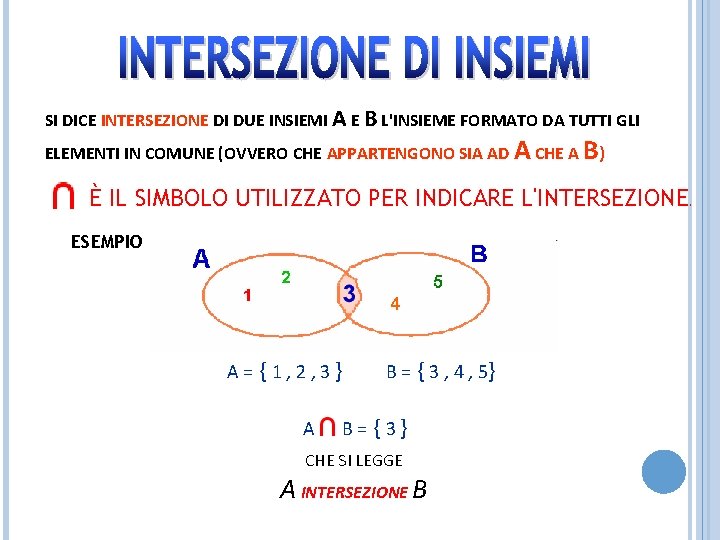
SI DICE INTERSEZIONE DI DUE INSIEMI A E B L'INSIEME FORMATO DA TUTTI GLI ELEMENTI IN COMUNE (OVVERO CHE APPARTENGONO SIA AD A CHE A B) È IL SIMBOLO UTILIZZATO PER INDICARE L'INTERSEZIONE. ESEMPIO A={1, 2, 3} A B = { 3 , 4 , 5} B={3} CHE SI LEGGE A INTERSEZIONE B

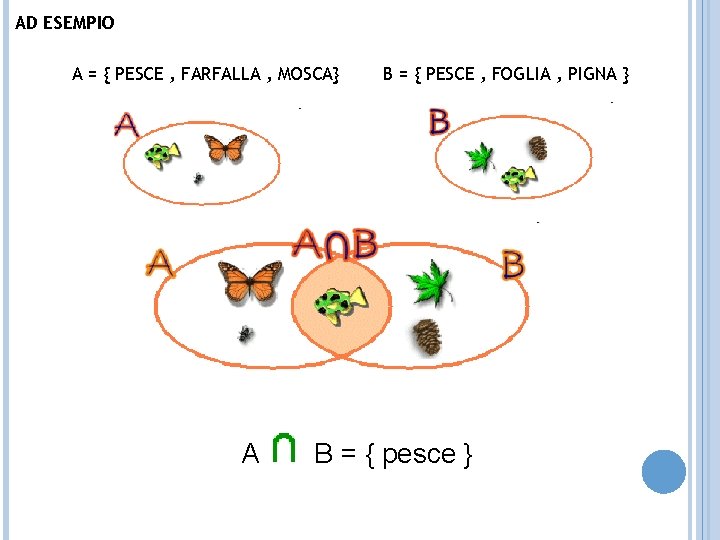
AD ESEMPIO A = { PESCE , FARFALLA , MOSCA} A B = { PESCE , FOGLIA , PIGNA } B = { pesce }

B A . o. l . v . a. c A. rosa. bianco. verde VEDIAMO QUALCHE ALTRO ESEMPIO DI INTERSEZIONE DI INSIEMI . blu. viola lo. gial . n. e . nero. azzurro. rosso B

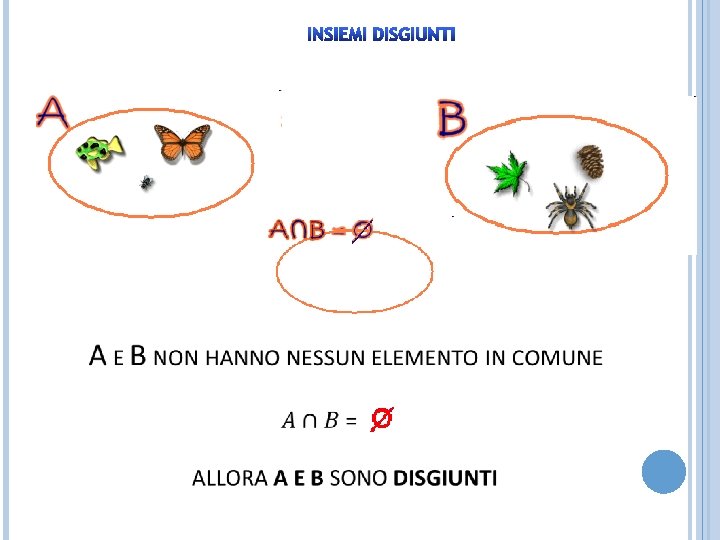
INSIEMI DISGIUNTI

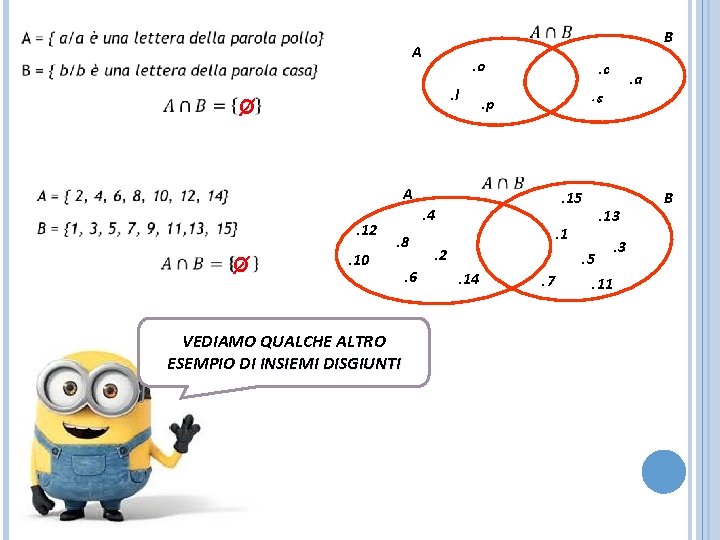
B A . o. l . c. s . p A. 12. 10 . 15 . 4. 8 VEDIAMO QUALCHE ALTRO ESEMPIO DI INSIEMI DISGIUNTI . 6 . 13 . 1. 2 . 5. 14 . a . 7 . 11 . 3 B

CONSIDERIAMO L’INSIEME A DELLE VOCALI E L’INSIEME B DEI NOMI DEGLI ORGANI SU SENSO A = {a, e, i, o, u} B = {vista, udito, gusto, tatto, olfatto} SE LI RAPPRESENTIAMO CON DIAGRAMMI DI EULERO-VENN, E COLLEGHIAMO TRA LORO GLI ELEMENTI, CI ACCORGIAMO CHE A OGNI ELEMENTO DI UNO DEI DUE INSIEMI È ASSOCIATO UN SOLO ELEMENTO DELL’ALTRO INSIEME E VICEVERSA. NOTIAMO CHE L’INSIEME A HA TANTI ELEMENTI QUANTI NE HA L’INSIEME B.

I DUE INSIEMI A E B HANNO LA STESSA QUANTITÀ DI ELEMENTI CIOÈ LA STESSA POTENZA, PERCIÒ SI DICONO EQUIPOTENTI LA POTENZA DI UN INSIEME SI CHIAMA ANCHE CARDINALITÀ O CARDINALE DELL’INSIEME. IL NUMERO È IL SIMBOLO CHE ESPRIME QUANTI SONO GLI ELEMENTI DI UN INSIEME E DI OGNI ALTRO INSIEME A ESSO EQUIPOTENTE IL NUMERO CHE ESPRIME LA CARDINALITÀ DELL’INSIEME: § A={ } è 0; § B={elefante} è 1; § C={cavallo, cane} è 2; § D={giraffa, tigre, leone} è 3.

A = { a/a è una lettera della parola pollo} GLI INSIEMI A E B SONO EQUIPOTENTI B = { b/b è una lettera della parola cassa} LA LORO CARDINALITÀ È 5 C = { c/c è un mese di 40 giorni} GLI INSIEMI C E D SONO EQUIPOTENTI D = { d/d è una consonante della parola aia} LA LORO CARDINALITÀ È 0 M = { bianco, rosso, verde} L = {il, lo, la } VEDIAMO QUALCHE ALTRO ESEMPIO GLI INSIEMI M E L SONO EQUIPOTENTI LA LORO CARDINALITÀ È 3

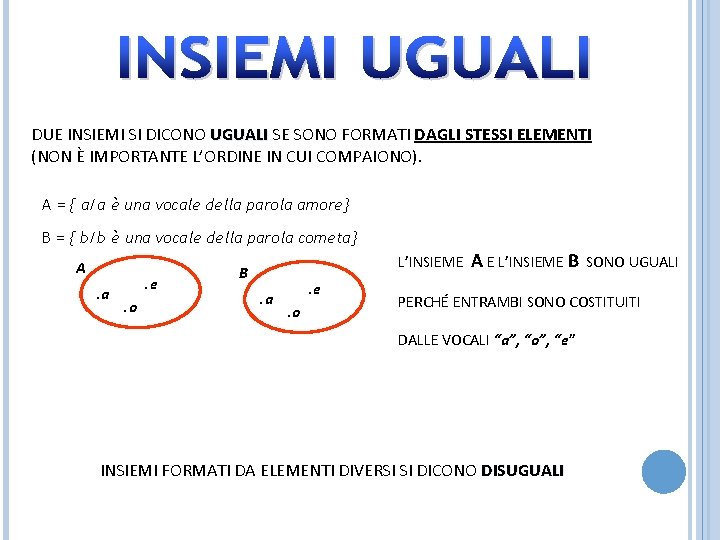
DUE INSIEMI SI DICONO UGUALI SE SONO FORMATI DAGLI STESSI ELEMENTI (NON È IMPORTANTE L’ORDINE IN CUI COMPAIONO). A = { a/a è una vocale della parola amore} B = { b/b è una vocale della parola cometa} A. a . e. o L’INSIEME B. a . e. o A E L’INSIEME B SONO UGUALI PERCHÉ ENTRAMBI SONO COSTITUITI DALLE VOCALI “a”, “o”, “e” INSIEMI FORMATI DA ELEMENTI DIVERSI SI DICONO DISUGUALI

SIMBOLO SIGNIFICATO INSIEME FORMATO DAGLI ELEMENTI a, b, c, INSIEME VUOTO APPARTIENE A… NON APPARTIENE A… INSIEMI SI DICONO UGUALI SE SONO ⊂ È SOTTOINSIEME, È INCLUSO ⊂ NON È INCLUSO Ã(A) INSIEME DELLE PARTI UNIONE INTERSEZIONE