GLI INSIEMI Dispensa a cura del prof CAVAGNA

GLI INSIEMI Dispensa a cura del prof. CAVAGNA GIANCARLO Luglio 2002

Presentazione Questa dispensa nasce come supporto alla lezione. Il docente può integrare le proprie spiegazioni proiettando le diapositive anche non in sequenza. Animazioni e chiarezza grafica sono sicuramente da considerarsi aspetti vantaggiosi rispetto agli strumenti tradizionali. Le animazioni inoltre, possono aiutare lo studente nell’apprendimento graduale del concetto. Questa presentazione può anche essere utilizzata come valido supporto allo studio. L’allievo può utilizzarla per rivedere autonomamente le parti fondamentali dell’unità didattica. Sono state inoltre introdotte alcune diapositive di approfondimento sugli insiemi infiniti e i paradossi che ne derivano, queste diapositive richiedono il sostegno di una spiegazione. Vengono infine proposti alcuni esercizi grazie ai quali l’allievo può autoverificare il proprio grado di preparazione.

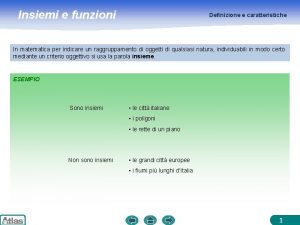
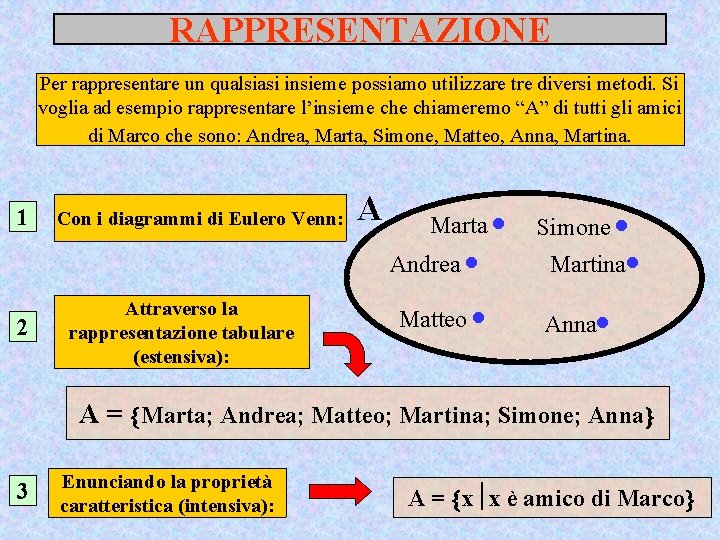
RAPPRESENTAZIONE Per rappresentare un qualsiasi insieme possiamo utilizzare tre diversi metodi. Si voglia ad esempio rappresentare l’insieme chiameremo “A” di tutti gli amici di Marco che sono: Andrea, Marta, Simone, Matteo, Anna, Martina. 1 Con i diagrammi di Eulero Venn: A Marta Andrea 2 Attraverso la rappresentazione tabulare (estensiva): Matteo Simone Martina Anna A = Marta; Andrea; Matteo; Martina; Simone; Anna 3 Enunciando la proprietà caratteristica (intensiva): A = x x è amico di Marco

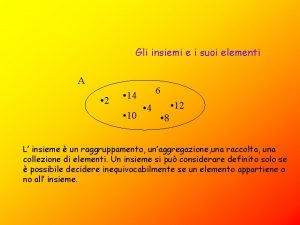
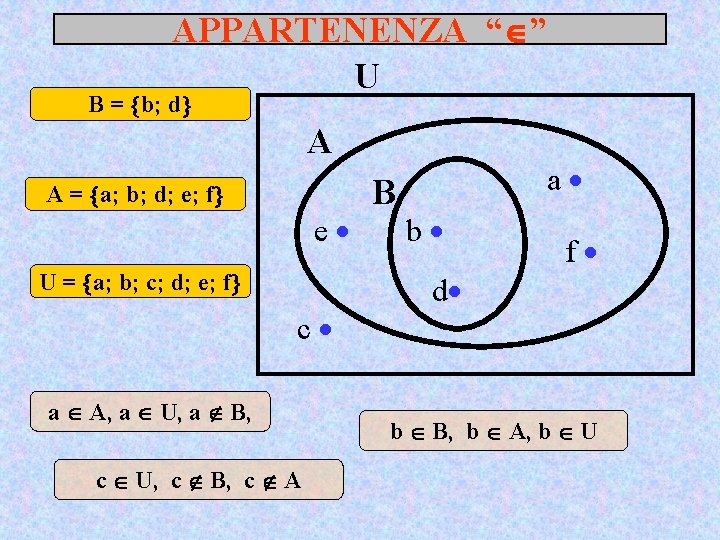
APPARTENENZA “ ” U B = b; d A A = a; b; d; e; f e U = a; b; c; d; e; f c a A, a U, a B, c U, c B, c A B a b f d b B, b A, b U

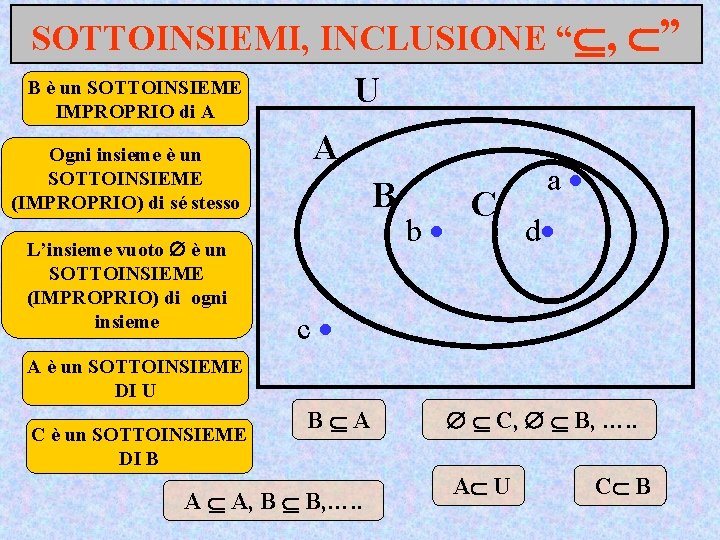
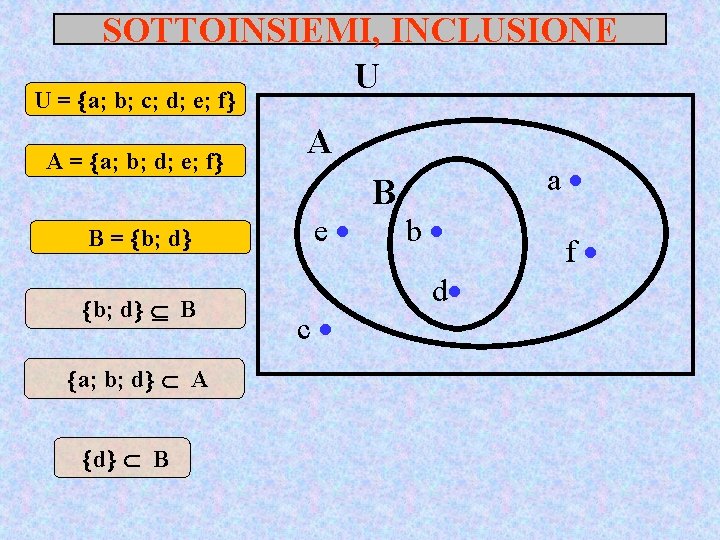
SOTTOINSIEMI, INCLUSIONE “ , B è un SOTTOINSIEME U IMPROPRIO di A Ogni insieme è un SOTTOINSIEME (IMPROPRIO) di sé stesso L’insieme vuoto è un SOTTOINSIEME (IMPROPRIO) di ogni insieme A B b C ” a d c A è un SOTTOINSIEME DI U C è un SOTTOINSIEME DI B B A A A, B B, …. . C, B, …. . A U C B

SOTTOINSIEMI, INCLUSIONE U U = a; b; c; d; e; f A = a; b; d; e; f B = b; d B a; b; d A d B A e c B a b d f

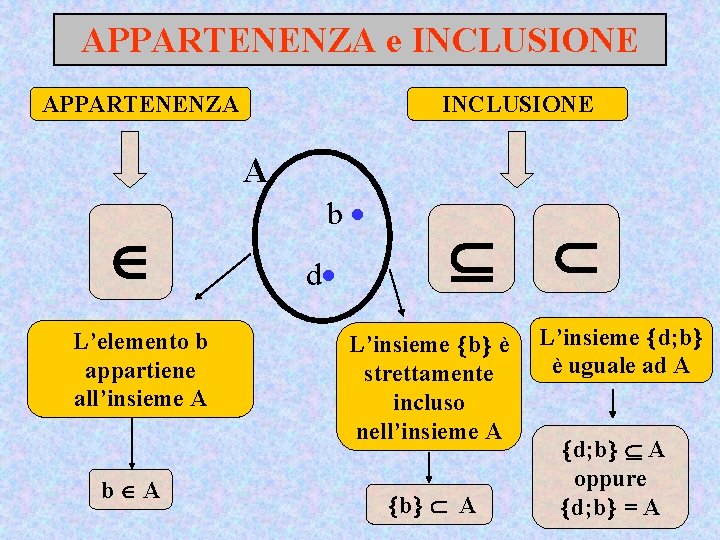
APPARTENENZA e INCLUSIONE APPARTENENZA INCLUSIONE A L’elemento b appartiene all’insieme A b d L’insieme b è strettamente incluso nell’insieme A b A L’insieme d; b è uguale ad A d; b A oppure d; b = A

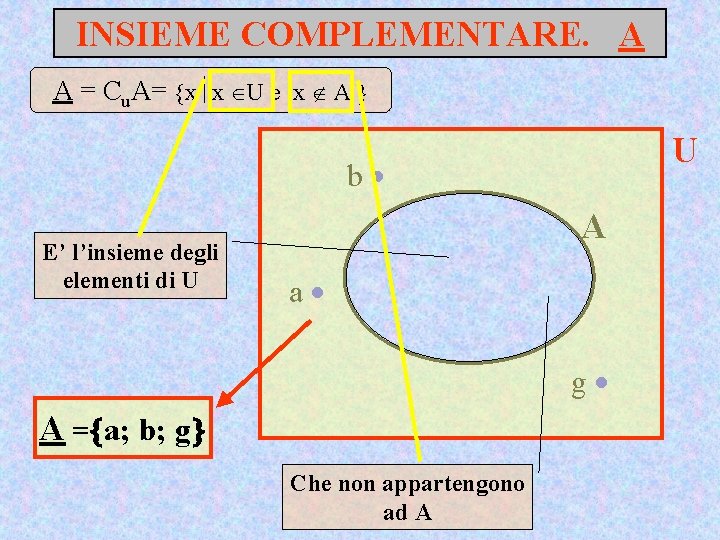
INSIEME COMPLEMENTARE. A A = Cu. A= x x U e x A U b E’ l’insieme degli elementi di U a c d f e A g A = a; b; g Che non appartengono ad A

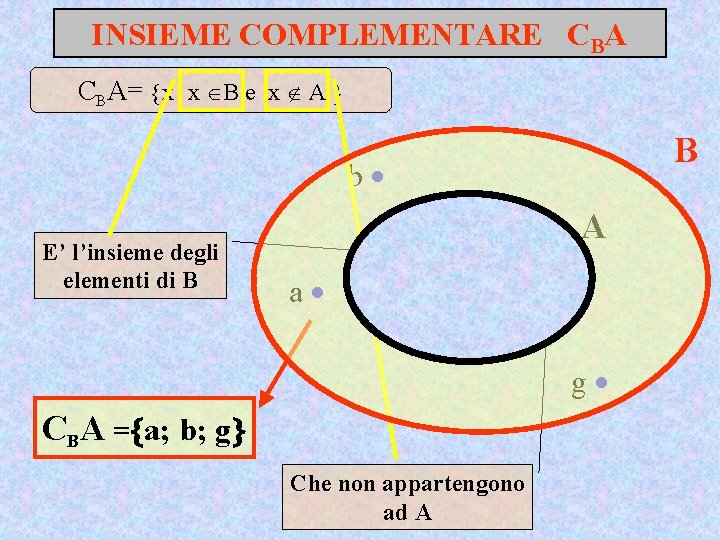
INSIEME COMPLEMENTARE CBA= x x B e x A B b E’ l’insieme degli elementi di B a c d f e A g CBA = a; b; g Che non appartengono ad A

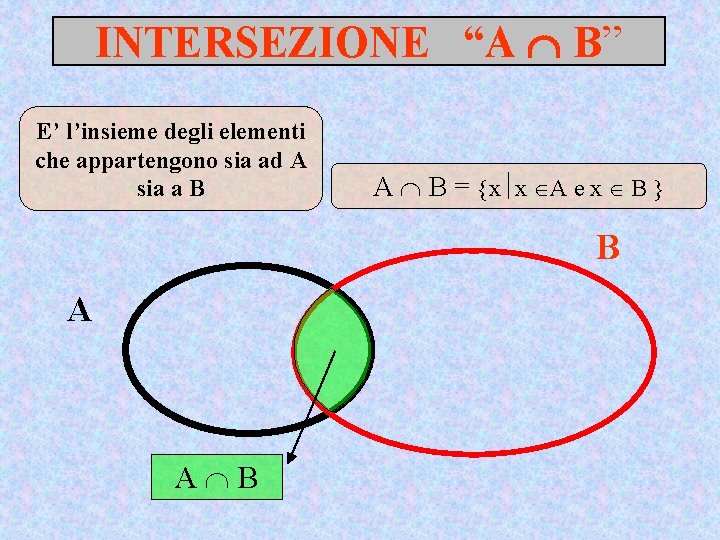
INTERSEZIONE “A B” E’ l’insieme degli elementi che appartengono sia ad A sia a B A B = x x A e x B B A A B

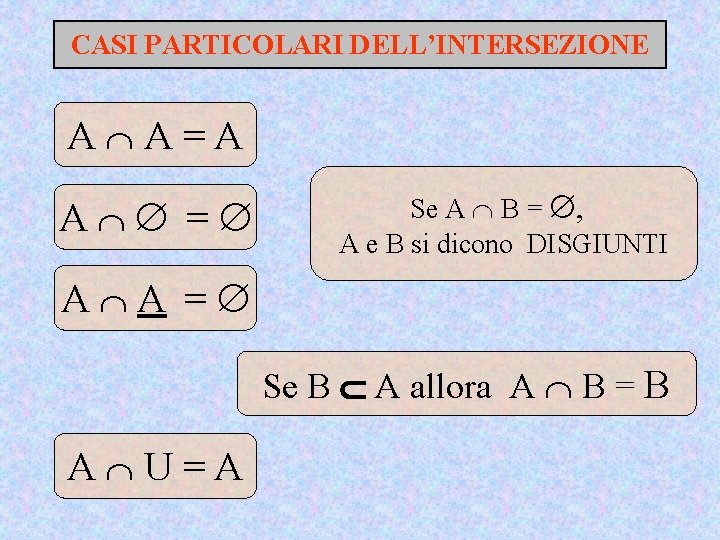
CASI PARTICOLARI DELL’INTERSEZIONE A A=A A = Se A B = , A e B si dicono DISGIUNTI A A = Se B A allora A B = B A U=A

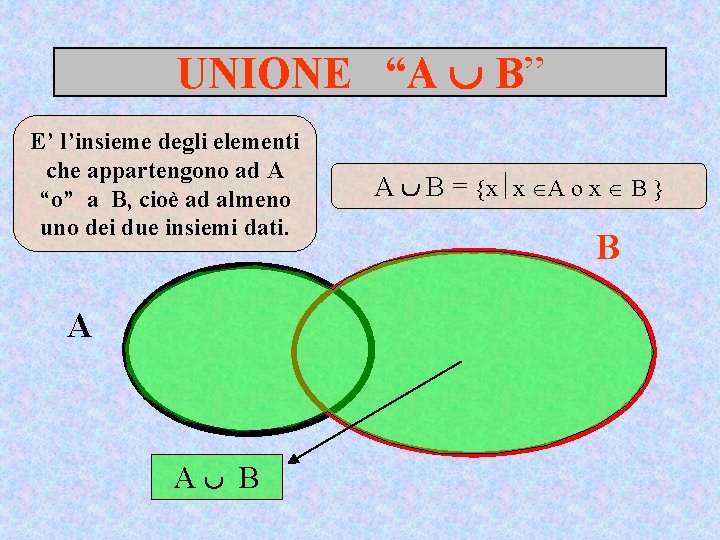
UNIONE “A B” E’ l’insieme degli elementi che appartengono ad A “o” a B, cioè ad almeno uno dei due insiemi dati. A A B A B = x x A o x B B

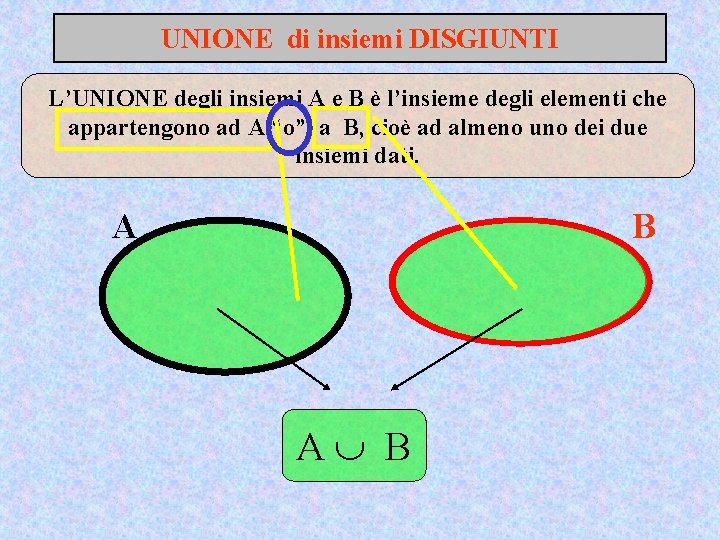
UNIONE di insiemi DISGIUNTI L’UNIONE degli insiemi A e B è l’insieme degli elementi che appartengono ad A “o” a B, cioè ad almeno uno dei due insiemi dati. A B

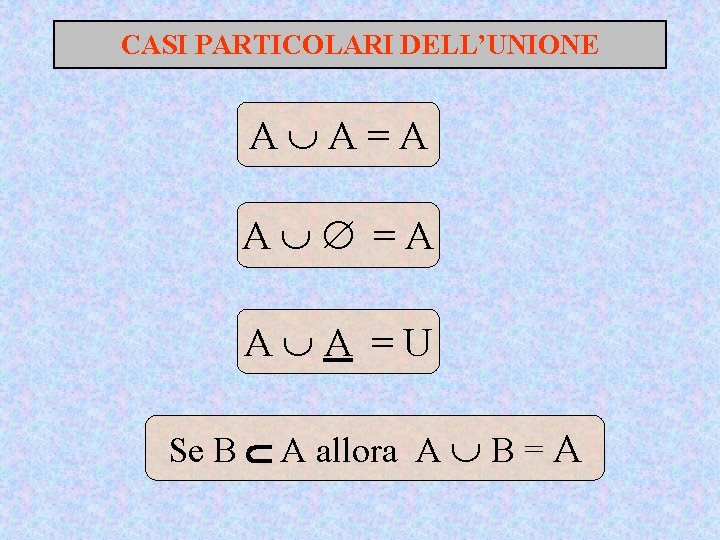
CASI PARTICOLARI DELL’UNIONE A A=A A A =U Se B A allora A B = A

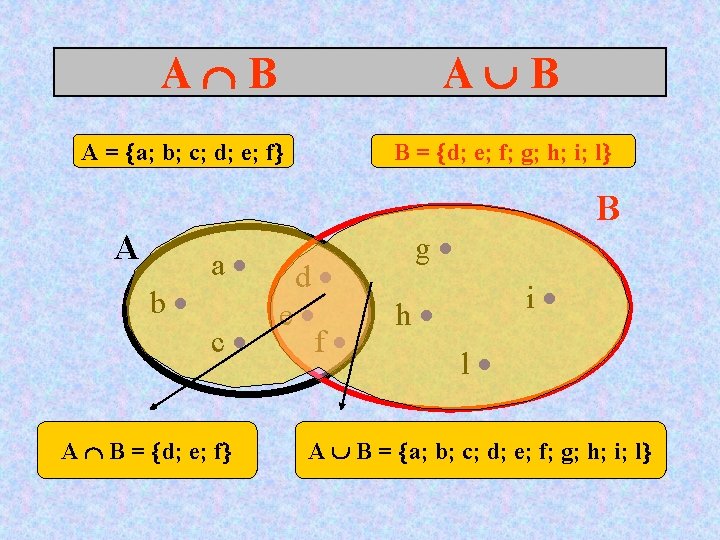
A B A = a; b; c; d; e; f A a B = d; e; f; g; h; i; l d b e c f A B = d; e; f B g i h l A B = a; b; c; d; e; f; g; h; i; l

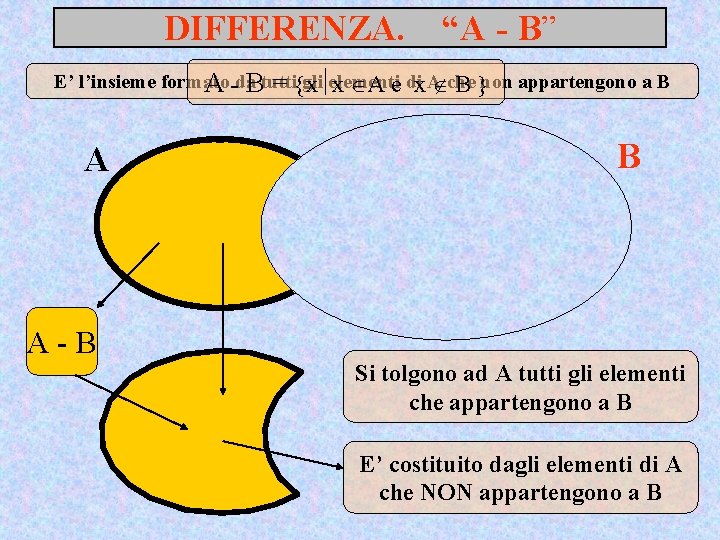
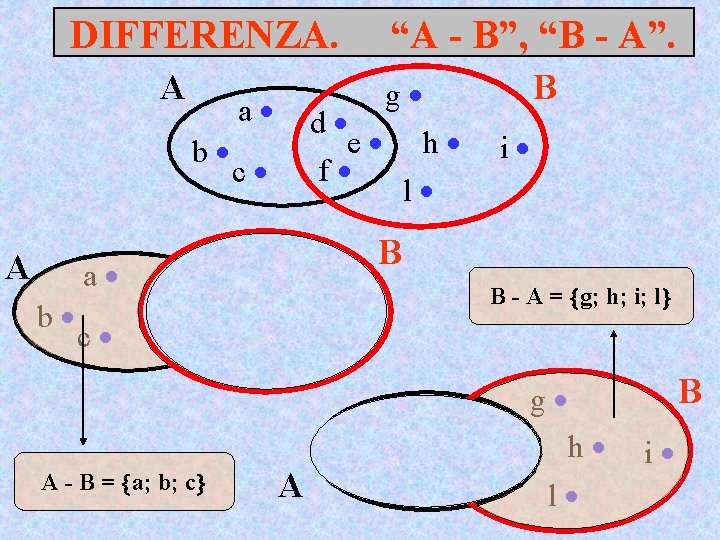
DIFFERENZA. “A - B” E’ l’insieme formato gli elementi A -da. Btutti = x x A e dix A che B non appartengono a B A A-B B Si tolgono ad A tutti gli elementi che appartengono a B E’ costituito dagli elementi di A che NON appartengono a B

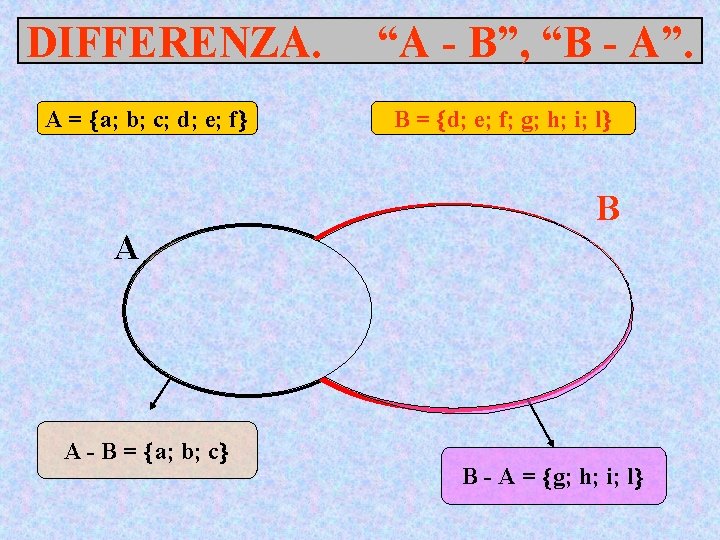
DIFFERENZA. A = a; b; c; d; e; f A a d b e c f A - B = a; b; c “A - B”, “B - A”. B = d; e; f; g; h; i; l B g i h l B - A = g; h; i; l

DIFFERENZA. A A a b c g d e h f l a b “A - B”, “B - A”. c g d e h f l A i B B - A = g; h; i; l i a A - B = a; b; c B b c g d e h f l B i

CASI PARTICOLARI DELLA DIFFERENZA TRA INSIEMI A-A= A- =A Se A B = allora A - B = A e B - A = B Se B A allora B - A =

INSIEME DELLE PARTI “P(A)” Dato un insieme A, l’insieme di tutti i suoi SOTTOINSIEMI propri e impropri, si definisce insieme delle parti di A e si indica A = a; b; c; A b a a con P(A) I possibili SOTTOINSIEMI di A L’insieme delle parti di A è: sono: c b c a; b a; c b; c a; b; c P(A) = ; a ; b ; c ; a; b ; a; c ; b; c ; a; b; c Gli elementi di P(A) sono INSIEMI Se A contiene n elementi, P(A) ne contiene 2 n

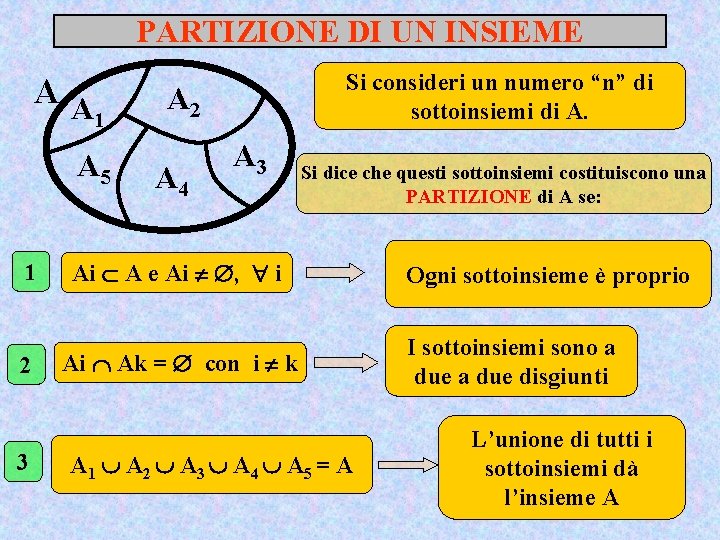
PARTIZIONE DI UN INSIEME AA 1 A 5 1 2 3 Si consideri un numero “n” di sottoinsiemi di A. A 2 A 4 A 3 Si dice che questi sottoinsiemi costituiscono una PARTIZIONE di A se: Ai A e Ai , i Ai Ak = con i k A 1 A 2 A 3 A 4 A 5 = A Ogni sottoinsieme è proprio I sottoinsiemi sono a due disgiunti L’unione di tutti i sottoinsiemi dà l’insieme A

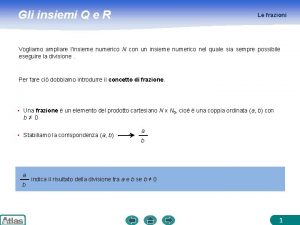
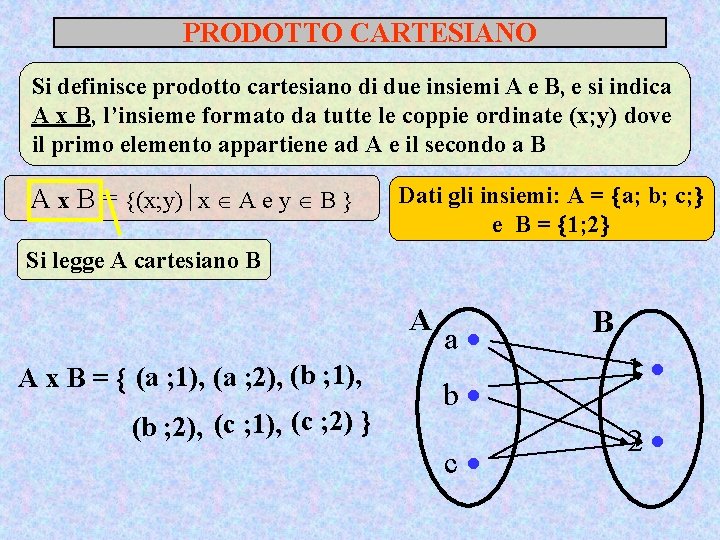
PRODOTTO CARTESIANO Si definisce prodotto cartesiano di due insiemi A e B, e si indica A x B, l’insieme formato da tutte le coppie ordinate (x; y) dove il primo elemento appartiene ad A e il secondo a B A x B = (x; y) x A e y B Dati gli insiemi: A = a; b; c; e B = 1; 2 Si legge A cartesiano B A A x B = (a ; 1), (a ; 2), (b ; 1), (b ; 2), (c ; 1), (c ; 2) a b c B 1 2

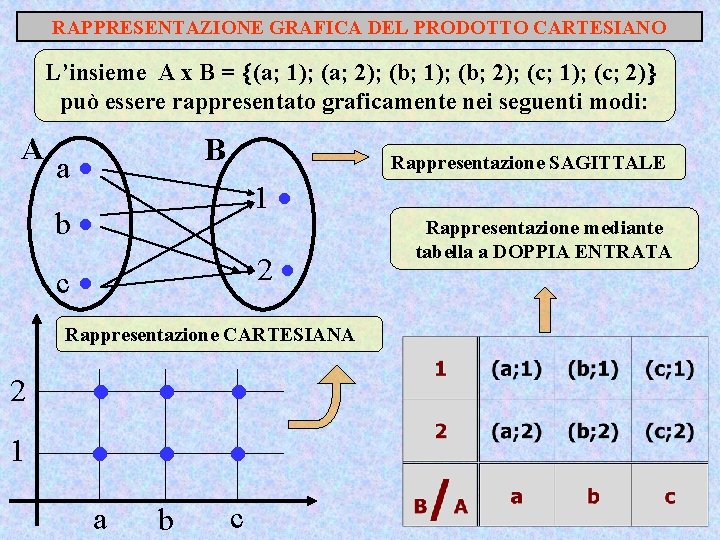
RAPPRESENTAZIONE GRAFICA DEL PRODOTTO CARTESIANO L’insieme A x B = (a; 1); (a; 2); (b; 1); (b; 2); (c; 1); (c; 2) può essere rappresentato graficamente nei seguenti modi: A B a Rappresentazione SAGITTALE 1 b 2 c Rappresentazione CARTESIANA 2 1 a b c Rappresentazione mediante tabella a DOPPIA ENTRATA

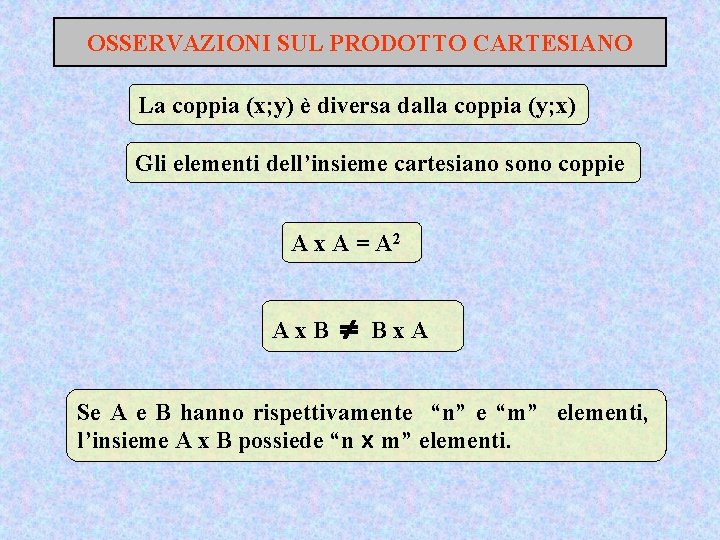
OSSERVAZIONI SUL PRODOTTO CARTESIANO La coppia (x; y) è diversa dalla coppia (y; x) Gli elementi dell’insieme cartesiano sono coppie A x A = A 2 Ax. B Bx. A Se A e B hanno rispettivamente “n” e “m” elementi, l’insieme A x B possiede “n x m” elementi.

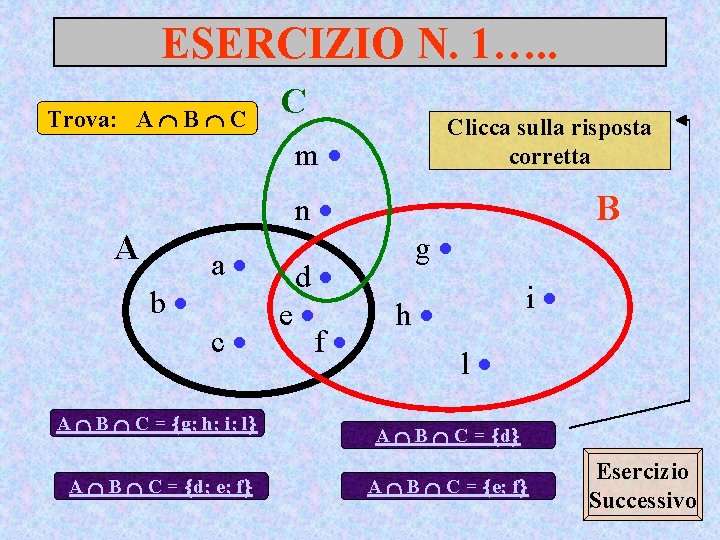
ESERCIZIO N. 1…. . Trova: A B C C Clicca sulla risposta corretta m n A a d b e c f A B C = g; h; i; l A B C = d; e; f B g i h l A B C = d A B C = e; f Esercizio Successivo

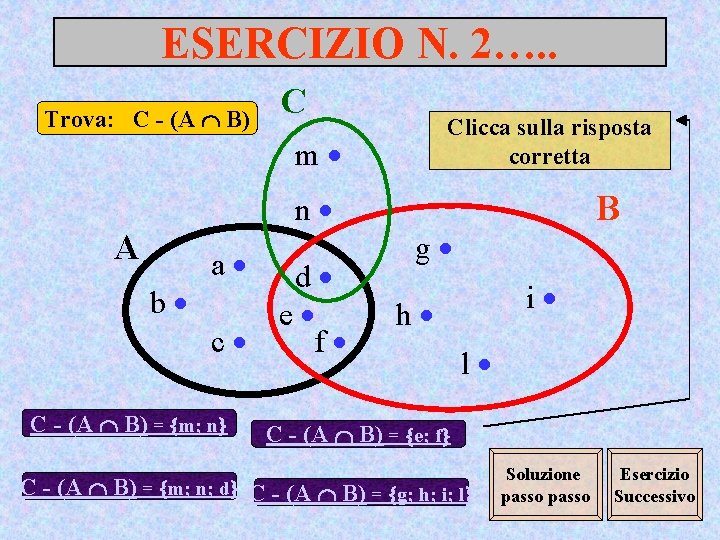
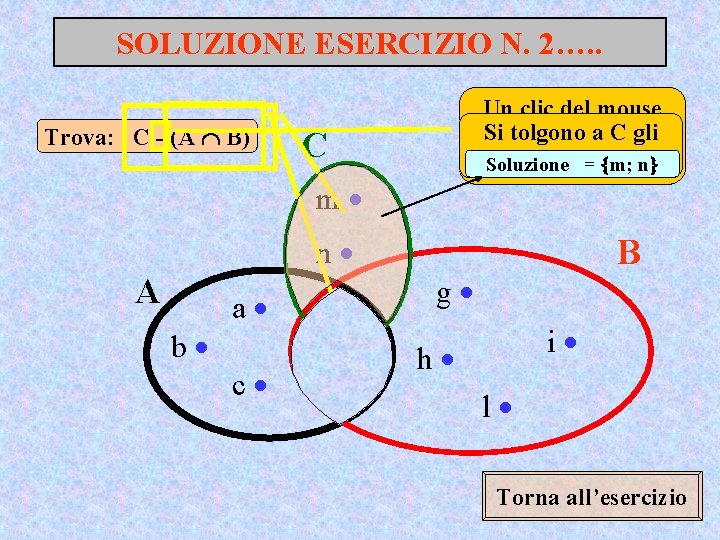
ESERCIZIO N. 2…. . Trova: C - (A B) C Clicca sulla risposta corretta m n A a d b e c f C - (A B) = m; n B g i h l C - (A B) = e; f C - (A B) = m; n; d C - (A B) = g; h; i; l Soluzione passo Esercizio Successivo

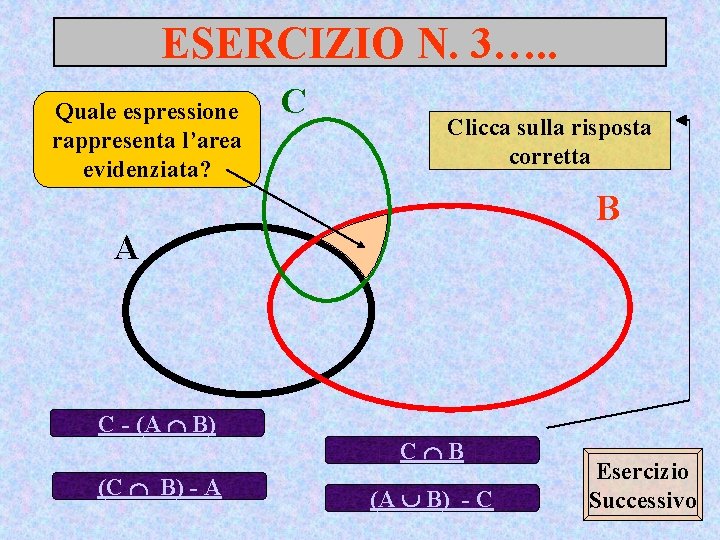
ESERCIZIO N. 3…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A C - (A B) (C B) - A C B (A B) - C Esercizio Successivo

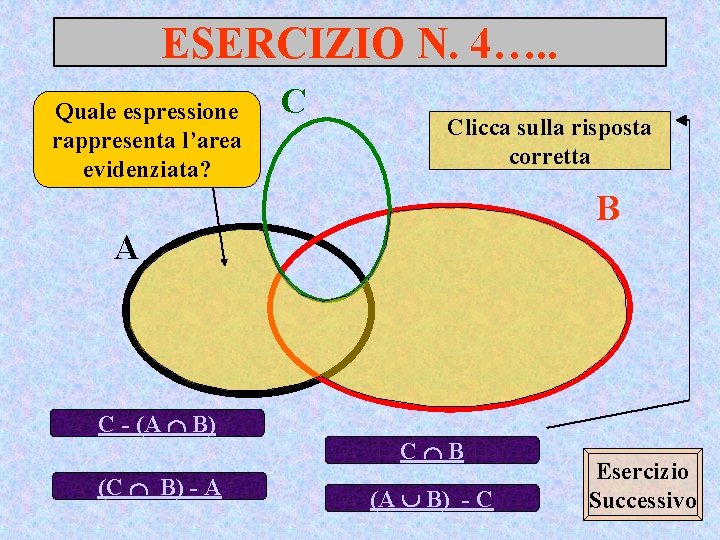
ESERCIZIO N. 4…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A C - (A B) (C B) - A C B (A B) - C Esercizio Successivo

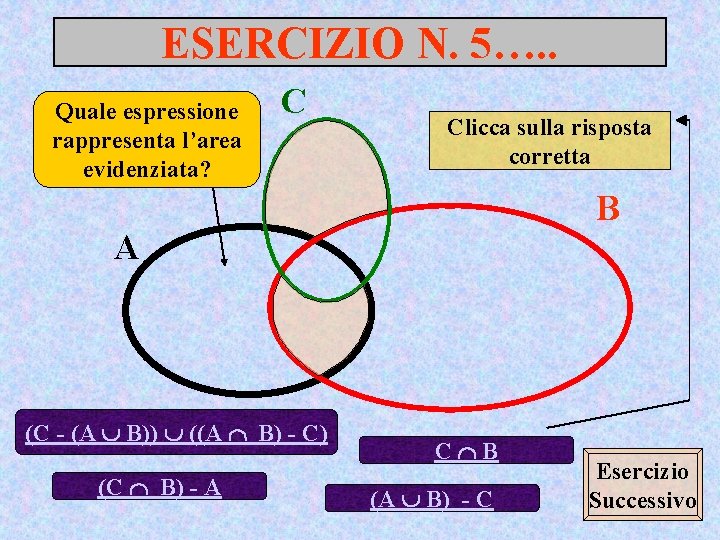
ESERCIZIO N. 5…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A (C - (A B)) ((A B) - C) (C B) - A C B (A B) - C Esercizio Successivo

RISPOSTE AI QUESITI

SOLUZIONE ESERCIZIO N. 2…. . Trova: C - (A B) Un clic del mouse Si tolgono a. C gli per avanzare passoelementi di= A n B Soluzione m; passo C m n A a d b e c f B g i h l Torna all’esercizio

TEORIA DEGLI INSIEMI COMPLIMENTI RISPOSTA ESATTA!!!! Ritorna alla diapositiva precedente

TEORIA DEGLI INSIEMI MI DISPIACE RISPOSTA ERRATA!!!! Ritorna alla diapositiva precedente