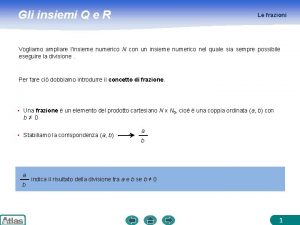
LINFINITO IN MATEMATICA Esempio 1 Dati gli insiemi

L’INFINITO IN MATEMATICA

Esempio 1 Dati gli insiemi L = {a, b, c, d, e, f} e M = {2, 3, 5, 10, 13, 17}, a 2 b 3 c 5 d 10 e 13 f 17 Osserviamo che vi è una corrispondenza biunivoca tra l’insieme L e l’insieme M.

Esempio 1 Siamo soliti dire che gli elementi di L sono tanti quelli di M. Se in M cancellassi 17, la corrispondenza non sarebbe biunivoca (una delle lettere dell’insieme L non avrebbe un corrispondente diverso da tutti i corrispondenti delle altre lettere). In questo caso gli elementi di M sarebbero di meno di quelli di L.

Esempio 2 Consideriamo l’insieme dei numeri naturali N e l’insieme dei numeri pari E. I numeri pari sono tanti quanti i numeri naturali? Ovviamente NO! Non consideriamo i numeri dispari, quindi sono di meno.

Esempio 2 Ma è un paradosso! Ma… 1 2 2 4 3 6 4 8 … n 2 n … Nel caso infinito, quindi, può succedere che un insieme abbia tanti elementi quanti un suo sottoinsieme proprio!

Uguaglianze sorprendenti Cosa si può dire di N e Z? Guardate un po’… 0 1 2 3 4 5 6 7 0 -1 +1 -2 +2 -3 +3 -4 In generale: a 0 corrisponde 0, a +n corrisponde 2 n, a –n corrisponde 2 n-1 Quindi Z ha tanti elementi quanti N.

Uguaglianze sorprendenti Ma sorprende ancora di più che Q abbia tanti elementi quanti ne ha N, anche se Q è denso e N è discreto. La dimostrazione di ciò scaturisce dal fatto che Q è un insieme ottenuto facendo il quoziente di Zx. Z con una congruenza (vedi I numeri razionali). Si dice che N, Z e Q sono insiemi numerabili.

Uguaglianze sorprendenti Ma succede lo stesso per R ed N?

Potenza del continuo TEOREMA L’insieme dei numeri reali R non è numerabile dimostrazione: Supponiamo per assurdo che R sia numerabile e rappresentiamo i numeri reali nella forma decimale. Tali numeri allora si possono numerare e siano: n 1, d 11 d 12 d 13 d 14… n 2, d 21 d 22 d 23 d 24… n 3, d 31 d 32 d 33 d 34… …

Potenza del continuo Costruiamo un numero diverso da tutti quelli elencati. Per esempio il numero m = 0, b 1 b 2 b 3 … dove b 1 è un numero della prima riga diverso da d 11, b 2 è un numero della seconda riga diverso da d 22, b 3 è un numero della terza riga diverso da d 33, e così via. È evidente che m differisce da tutti i numeri della tabella. Abbiamo così costruito un nuovo numero e la tesi è provata. Diremo quindi che R è un insieme non numerabile ma continuo.

Teorema di Cantor La scoperta di un’infinità maggiore di quella del numerabile indusse Cantor a ritenere che esistessero altri tipi di infinità. TEOREMA Dato un insieme A , l’insieme P (A) di tutti i suoi sottoinsiemi ha cardinalità maggiore di quella di A. Questo teorema è ovvio per insiemi finiti.

Teorema di Cantor dimostrazione: Sia f: A P (A) Basta provare che f non è suriettiva, cioè individuare un elemento di P (A) che non è nell’immagine di f. Questo elemento è: B={x є A | x non appartiene a f(x)} Supponiamo per assurdo che B sia nell’immagine di f. Allora, c’è un y in A tale che f(y)=B.

Teorema di Cantor Si possono distinguere due casi: 1. y non è in B 2. y è in B Nel caso 1, per la definizione di B, y appartiene a B. Nel caso 2, per la definizione di B, y non appartiene a B. In ogni caso si ha una contraddizione. Perciò il teorema è dimostrato.

Il teorema di Cantor ci permette di costruire insiemi di cardinalità sempre maggiore. Così P (N) ha cardinalità maggiore del numerabile. P (R) ha cardinalità maggiore di quella del continuo. P (P (R)), P (P (P (R)))…individuano insiemi di cardinalità sempre più grande. Purtroppo, però, Cantor non riuscì a dimostrare che non ci sono insiemi la cui cardinalità è più grande di quella del numerabile e nello stesso tempo più piccola di quella del continuo. Questo fatto viene detto ipotesi del continuo.