Processing Analysis of Geometric Shapes Introduction to Geometry

Processing & Analysis of Geometric Shapes Introduction to Geometry 1 Εισαγωγή Introduction στη toγεωμετρία geometry τηςThe ελληνικής Greek way τρόπο © Alexander & Michael Bronstein, 2006 -2009 © Michael Bronstein, 2010 tosca. cs. technion. ac. il/book 048921 Advanced topics in vision Processing and Analysis of Geometric Shapes EE Technion, Spring 2010

Processing & Analysis of Geometric Shapes Introduction to Geometry Raffaello Santi, School of Athens, Vatican 2

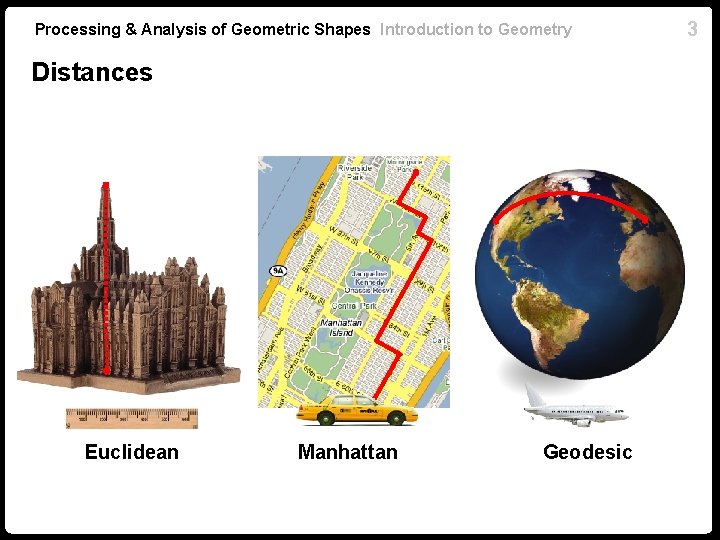
Processing & Analysis of Geometric Shapes Introduction to Geometry Distances Euclidean Manhattan Geodesic 3

4 Processing & Analysis of Geometric Shapes Introduction to Geometry Metric A function satisfying for all n Non-negativity: n Indiscernability: if and only if n Symmetry: n Triangle inequality: B is called a metric space A C AB BC + AC

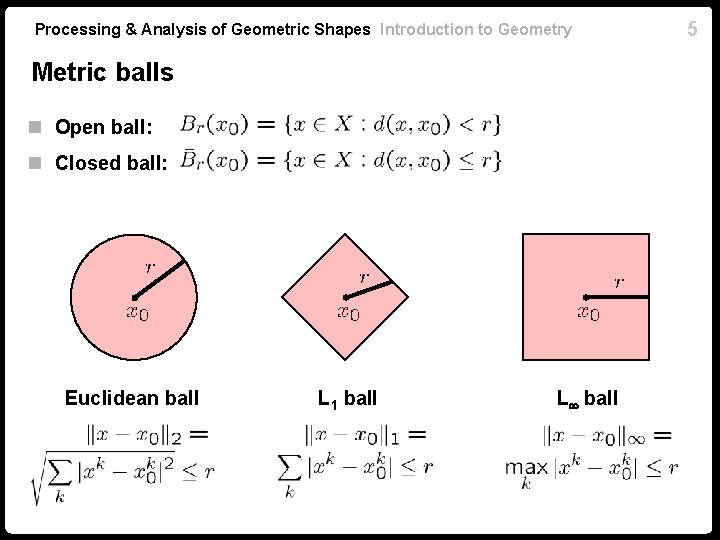
Processing & Analysis of Geometric Shapes Introduction to Geometry Metric balls n Open ball: n Closed ball: Euclidean ball L 1 ball L ball 5

Processing & Analysis of Geometric Shapes Introduction to Geometry Topology A set is open if for any there exists such that n Empty set is open n Union of any number of open sets is open n Finite intersection of open sets is open Collection of all open sets in is called topology The metric induces a topology through the definition of open sets Topology can be defined independently of a metric through an axiomatic definition of an open set 6

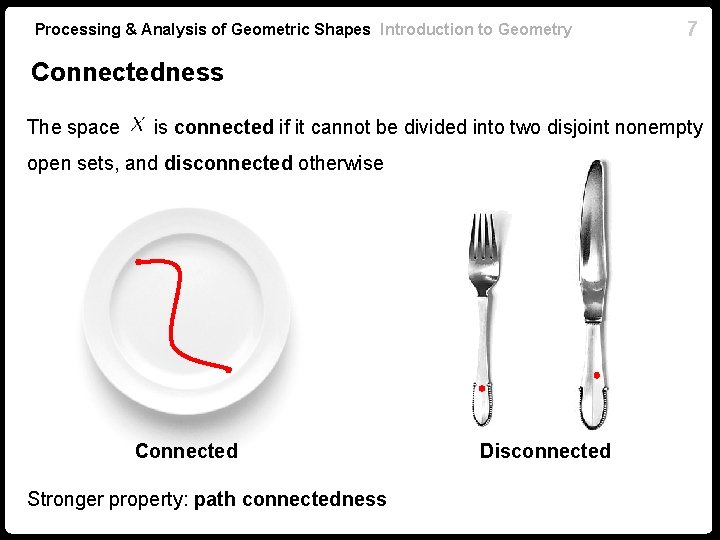
Processing & Analysis of Geometric Shapes Introduction to Geometry 7 Connectedness The space is connected if it cannot be divided into two disjoint nonempty open sets, and disconnected otherwise Connected Stronger property: path connectedness Disconnected

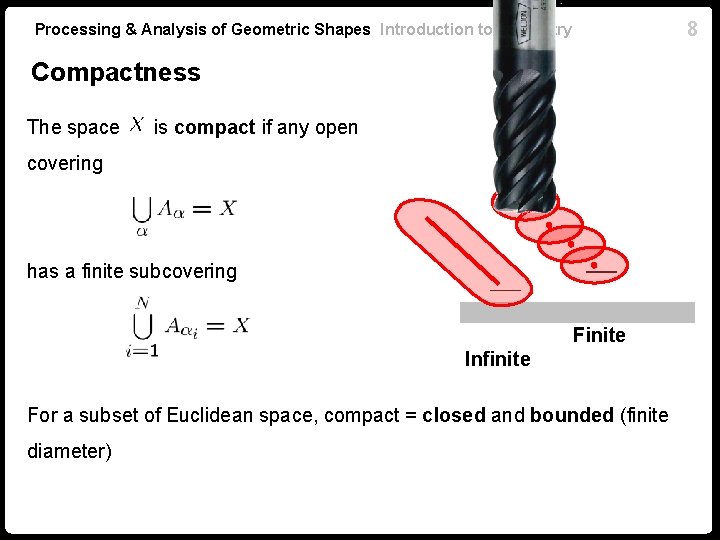
8 Processing & Analysis of Geometric Shapes Introduction to Geometry Compactness The space is compact if any open covering has a finite subcovering Finite Infinite For a subset of Euclidean space, compact = closed and bounded (finite diameter)

9 Processing & Analysis of Geometric Shapes Introduction to Geometry Convergence A sequence converges to for any open set exists containing such that for all Topological definition (denoted for all ) if exists such that for all Metric definition

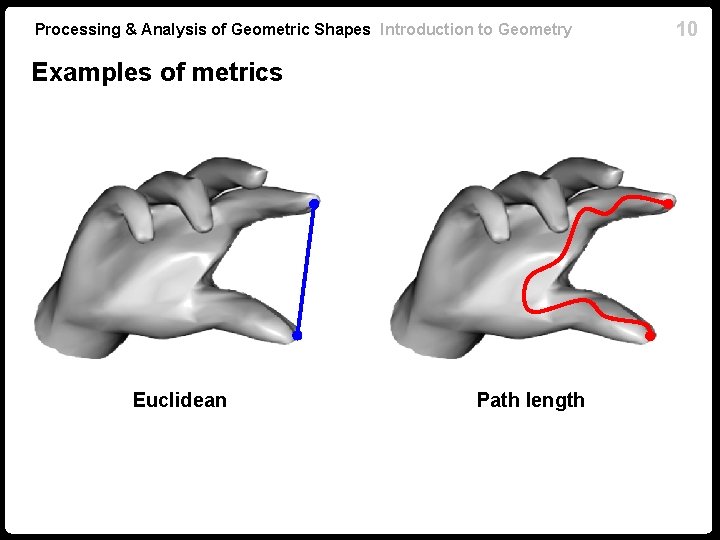
Processing & Analysis of Geometric Shapes Introduction to Geometry Examples of metrics Euclidean Path length 10

Processing & Analysis of Geometric Shapes Introduction to Geometry 11 Length spaces Path length , e. g. measured as time it takes to travel along the path Length metric is called a length space

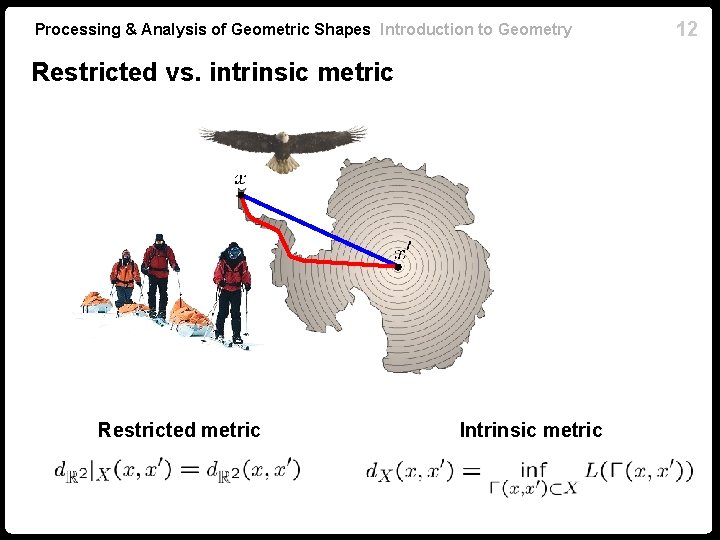
Processing & Analysis of Geometric Shapes Introduction to Geometry Restricted vs. intrinsic metric Restricted metric Intrinsic metric 12

Processing & Analysis of Geometric Shapes Introduction to Geometry Induced metric Path length is approximated as sum of lengths of line segments of which the path consists, measured using Euclidean metric The Euclidean metric induces a length metric Can induce another length metric? 13

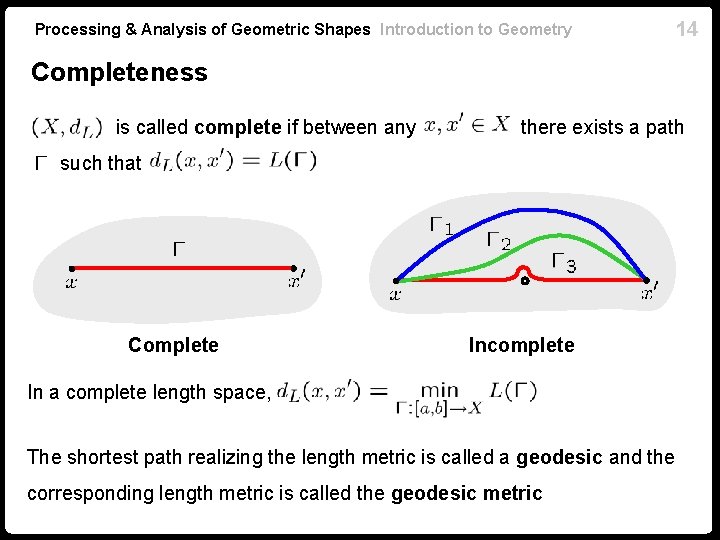
Processing & Analysis of Geometric Shapes Introduction to Geometry 14 Completeness is called complete if between any there exists a path such that Complete Incomplete In a complete length space, The shortest path realizing the length metric is called a geodesic and the corresponding length metric is called the geodesic metric

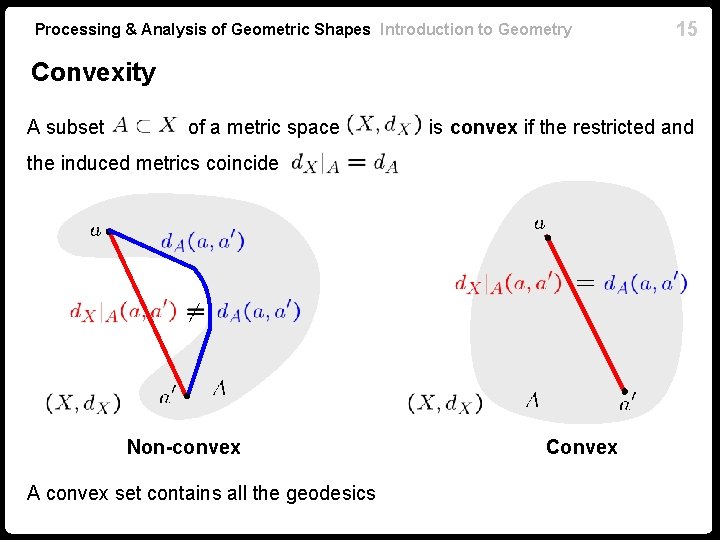
Processing & Analysis of Geometric Shapes Introduction to Geometry 15 Convexity A subset of a metric space is convex if the restricted and the induced metrics coincide Non-convex A convex set contains all the geodesics Convex

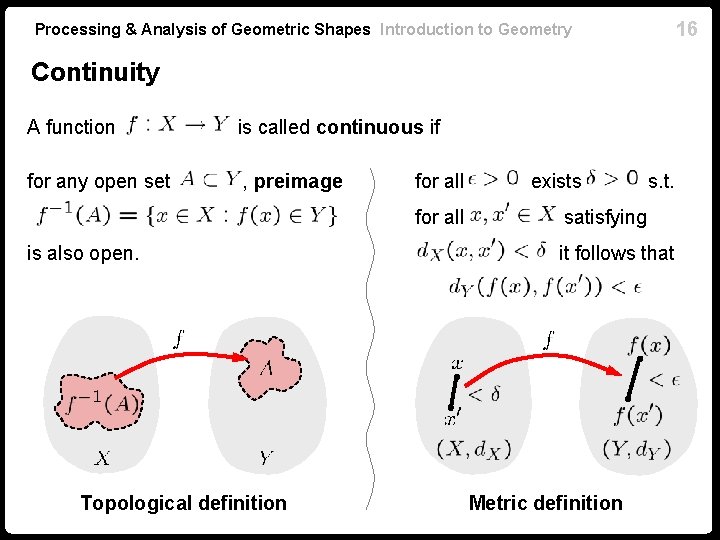
16 Processing & Analysis of Geometric Shapes Introduction to Geometry Continuity A function is called continuous if for any open set , preimage for all is also open. Topological definition exists s. t. satisfying it follows that Metric definition

Processing & Analysis of Geometric Shapes Introduction to Geometry 17 Properties of continuous functions n Map limits to limits, i. e. , if , then n Map open sets to open sets n Map compact sets to compact sets n Map connected sets to connected sets Continuity is a local property: a function can be continuous at one point and discontinuous at another

Processing & Analysis of Geometric Shapes Introduction to Geometry Homeomorphisms A bijective (one-to-one and onto) continuous function with a continuous inverse is called a homeomorphism Homeomorphisms copy topology – homeomorphic spaces are topologically equivalent Torus and cup are homeomorphic 18

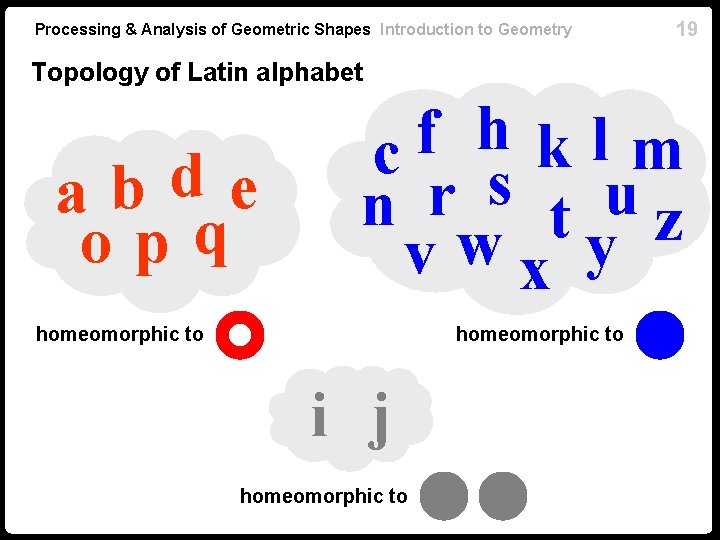
Processing & Analysis of Geometric Shapes Introduction to Geometry 19 Topology of Latin alphabet d b e a opq h f l k m c s n r t uz vwx y homeomorphic to i j homeomorphic to

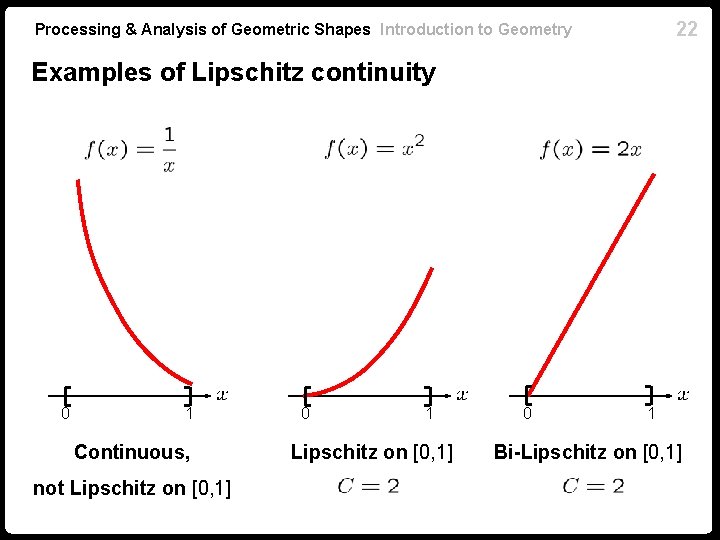
Processing & Analysis of Geometric Shapes Introduction to Geometry 20 Lipschitz continuity A function is called Lipschitz continuous if there exists a constant for all such that . The smallest possible is called Lipschitz constant Lipschitz continuous function does not change the distance between any pair of points by more than times Lipschitz continuity is a global property For a differentiable function

Processing & Analysis of Geometric Shapes Introduction to Geometry Bi-Lipschitz continuity A function there exists a constant for all is called bi-Lipschitz continuous if such that 21

22 Processing & Analysis of Geometric Shapes Introduction to Geometry Examples of Lipschitz continuity 0 1 Continuous, not Lipschitz on [0, 1] 0 1 Bi-Lipschitz on [0, 1]

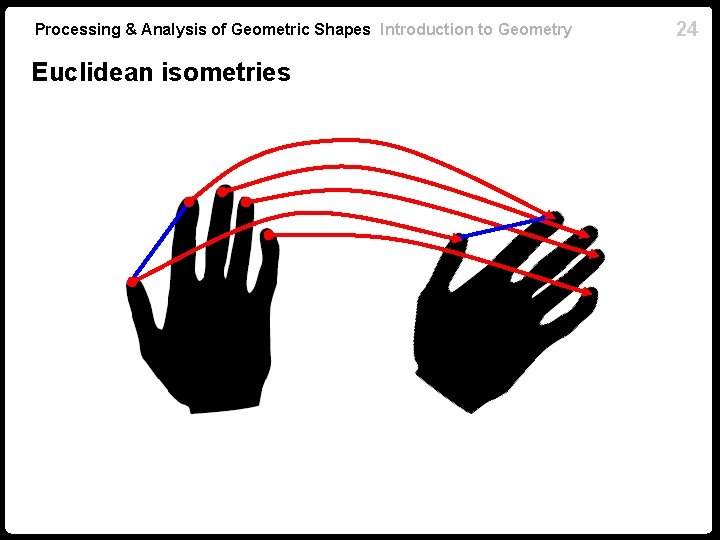
23 Processing & Analysis of Geometric Shapes Introduction to Geometry Isometries n Two metric spaces and are equivalent if there exists a distance-preserving map (isometry) n Such and satisfying are called isometric, denoted n Isometries copy metric geometries – isometric spaces are equivalent from the point of view of metric geometry

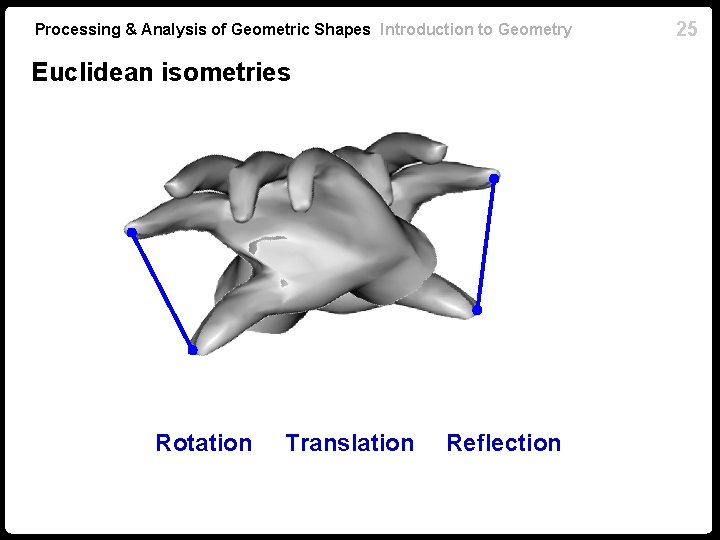
Processing & Analysis of Geometric Shapes Introduction to Geometry Euclidean isometries 24

Processing & Analysis of Geometric Shapes Introduction to Geometry Euclidean isometries Rotation Translation Reflection 25

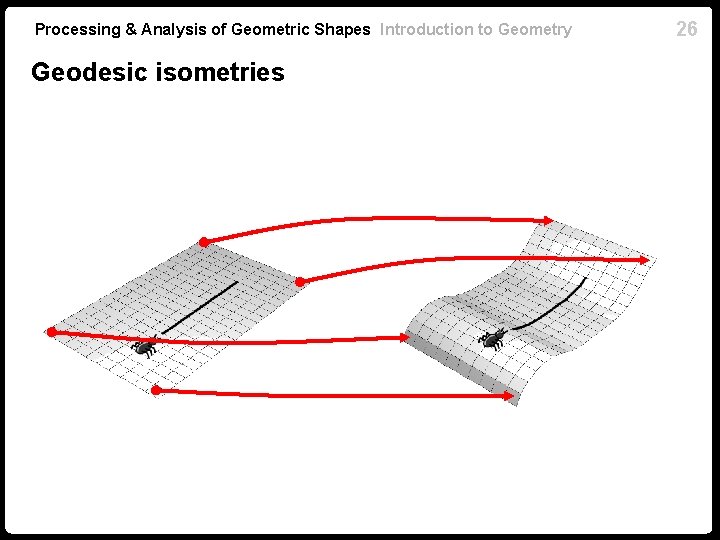
Processing & Analysis of Geometric Shapes Introduction to Geometry Geodesic isometries 26

Processing & Analysis of Geometric Shapes Introduction to Geometry 27 Groups A set with a binary operation is called a group if the following properties hold: n Closure: for all n Associativity: n Identity element: n Inverse element: for any for all such that , for all such that

Processing & Analysis of Geometric Shapes Introduction to Geometry 28 Examples of groups Integers with addition operation n Closure: sum of two integers is an integer n Associativity: n Identity element: n Inverse element: Non-zero real numbers with multiplication operation n Closure: product of two non-zero real numbers is a non-zero real number n Associativity: n Identity element: n Inverse element:

Processing & Analysis of Geometric Shapes Introduction to Geometry Self-sometries A function is called a self-isometry if for all Set of all self-isometries of is denoted by with the function composition operation n Closure is a group is a self-isometry for all n Associativity from definition of function composition n Identity element n Inverse element (exists because isometries are bijective) 29

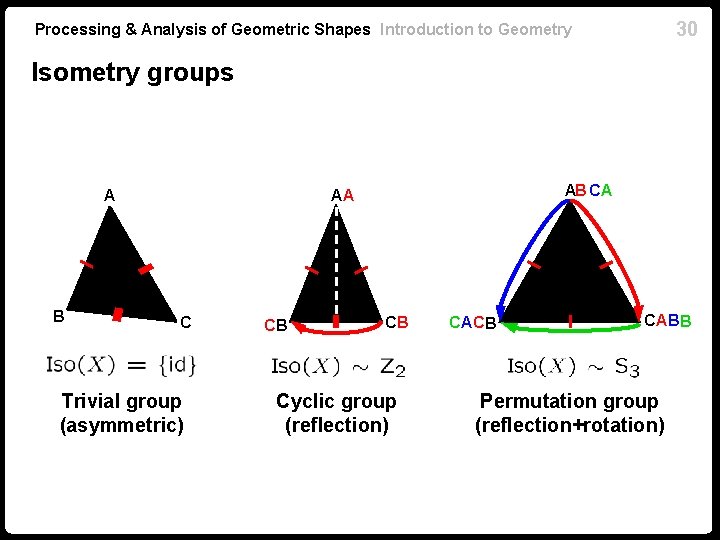
30 Processing & Analysis of Geometric Shapes Introduction to Geometry Isometry groups A B AB CA AA C Trivial group (asymmetric) CB CB Cyclic group (reflection) CACB CAB B Permutation group (reflection+rotation)

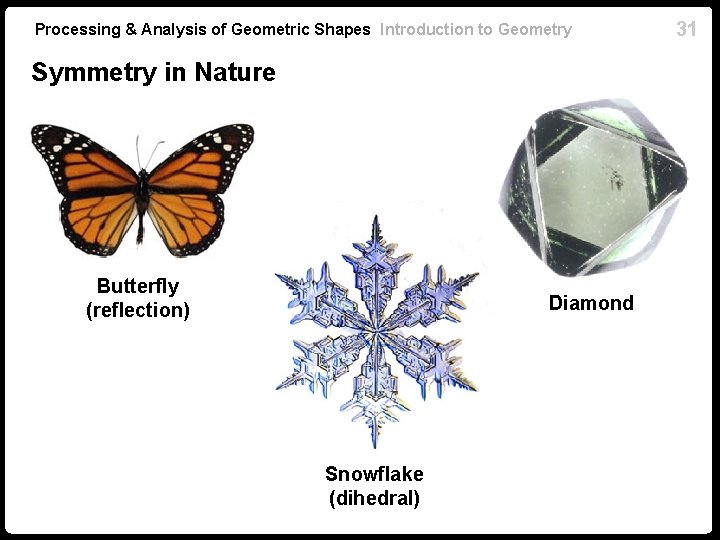
Processing & Analysis of Geometric Shapes Introduction to Geometry Symmetry in Nature Butterfly (reflection) Diamond Snowflake (dihedral) 31

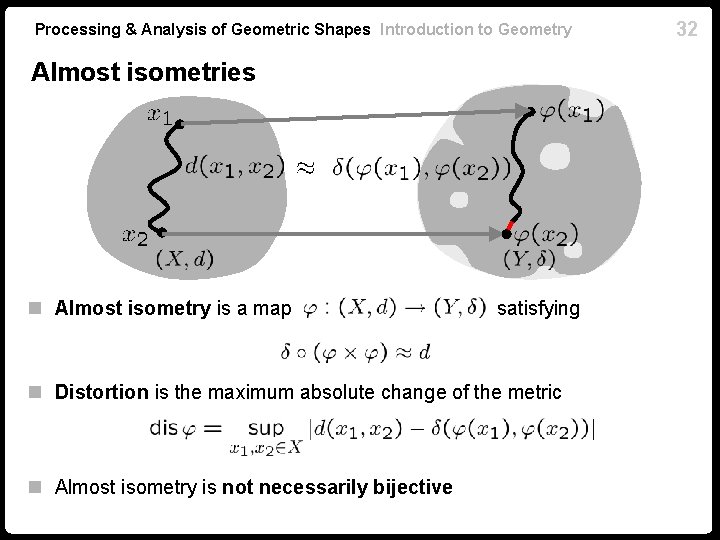
Processing & Analysis of Geometric Shapes Introduction to Geometry Almost isometries n Almost isometry is a map satisfying n Distortion is the maximum absolute change of the metric n Almost isometry is not necessarily bijective 32

Processing & Analysis of Geometric Shapes Introduction to Geometry Almost isometries 33

Processing & Analysis of Geometric Shapes Introduction to Geometry -isometries A function is an Isometry -isometry n Distance preserving n -distance preserving n Bijective (one-to-one and on) n -surjective n Continuous n Not necessarily continuous 34

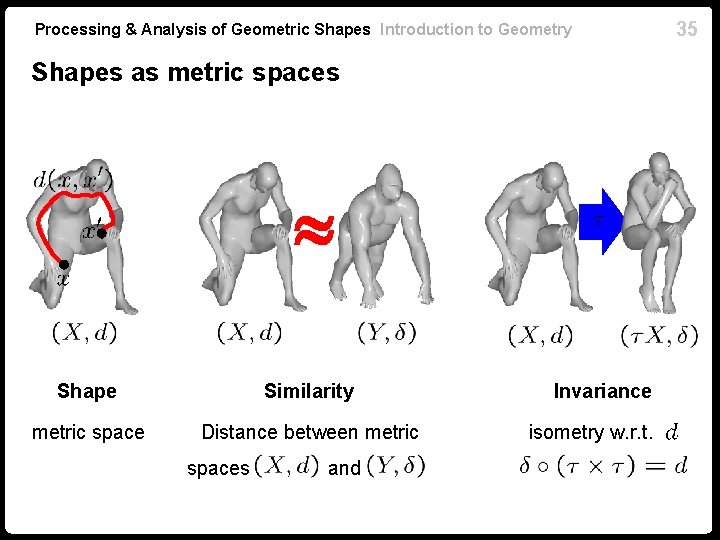
Processing & Analysis of Geometric Shapes Introduction to Geometry Shapes as metric spaces Shape Similarity metric space Distance between metric spaces and Invariance isometry w. r. t. . 35

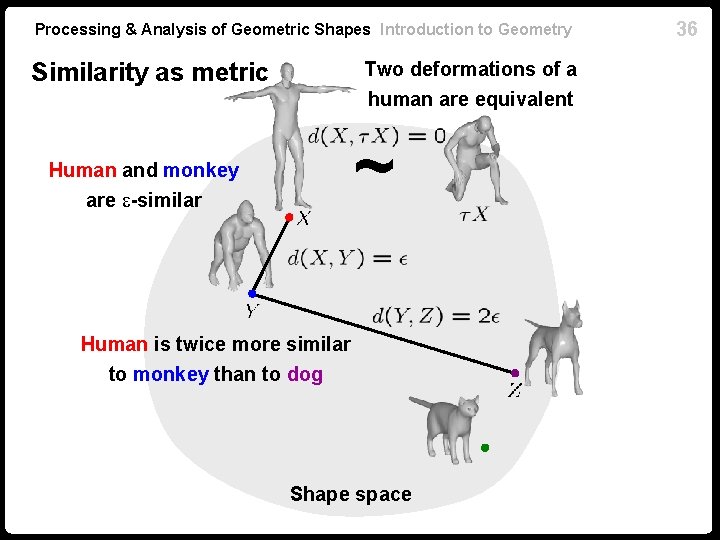
Processing & Analysis of Geometric Shapes Introduction to Geometry Similarity as metric Two deformations of a human are equivalent ~ Human and monkey are -similar Human is twice more similar to monkey than to dog Shape space 36

Processing & Analysis of Geometric Shapes Introduction to Geometry Recap n Metric is a generic notion of distance/dissimilarity n Metric induces topology n Continuous maps preserve topology n Isometric maps preserve metric and topology n Almost isometric maps preserve neither n Shapes as metric spaces (metric is invariant structure) n Shape spaces (metric is a notion of shape similarity) 37