Processing and Analysis of Geometric Shapes Discrete Geometry





























- Slides: 51

Processing and Analysis of Geometric Shapes Discrete Geometry Discrete geometry © Alexander & Michael Bronstein, 2006 -2009 © Michael Bronstein, 2010 tosca. cs. technion. ac. il/book 048921 Advanced topics in vision Processing and Analysis of Geometric Shapes EE Technion, Spring 2010

Processing and Analysis of Geometric Shapes Discrete Geometry ‘‘The world is continuous, ‘‘ but the mind is discrete David Mumford

Processing and Analysis of Geometric Shapes Discrete Geometry Discretization Continuous world Discrete world n Surface n Sampling n Metric n Discrete metric (matrix of distances) n Topology n Discrete topology (connectivity) 3

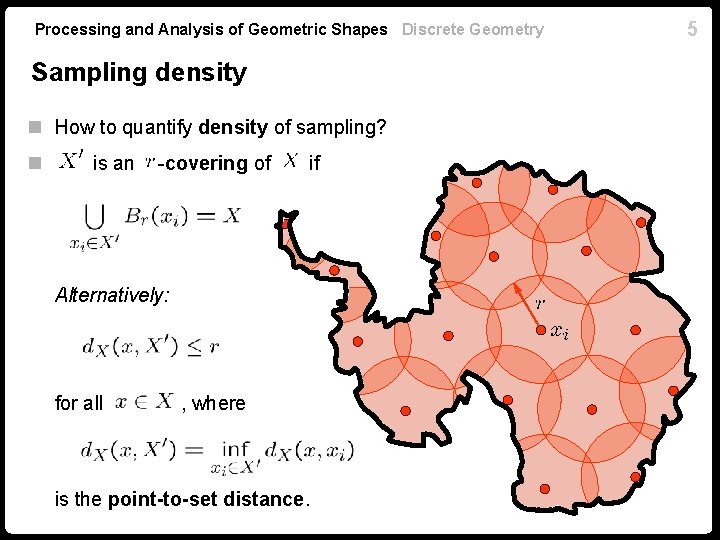
Processing and Analysis of Geometric Shapes Discrete Geometry How good is a sampling? 4

Processing and Analysis of Geometric Shapes Discrete Geometry Sampling density n How to quantify density of sampling? n is an -covering of if Alternatively: for all , where is the point-to-set distance. 5

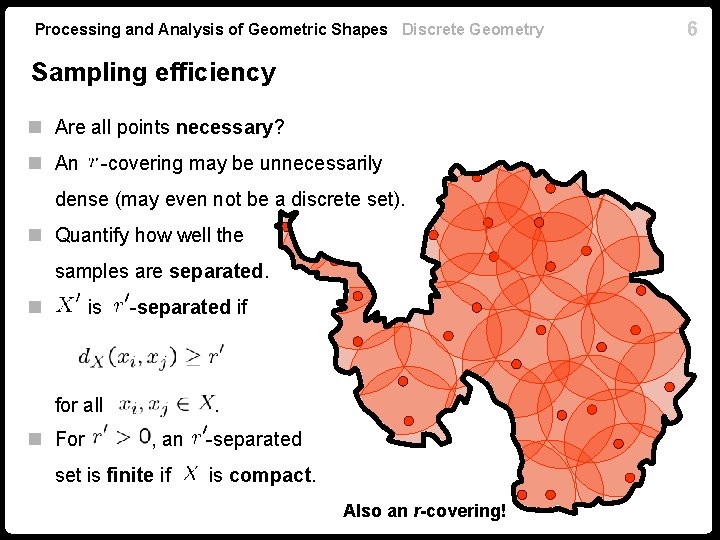
Processing and Analysis of Geometric Shapes Discrete Geometry Sampling efficiency n Are all points necessary? n An -covering may be unnecessarily dense (may even not be a discrete set). n Quantify how well the samples are separated. n is -separated if for all n For . , an set is finite if -separated is compact. Also an r-covering! 6

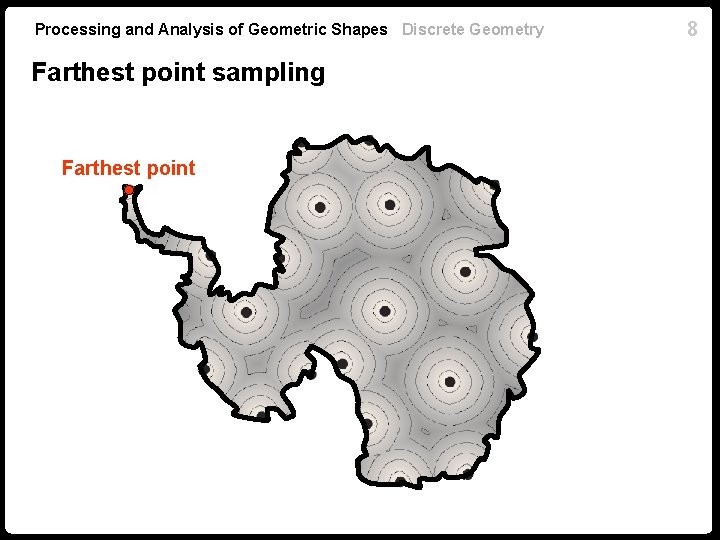
Processing and Analysis of Geometric Shapes Discrete Geometry Farthest point sampling n Good sampling has to be dense and efficient at the same time. n Find and -separated -covering n Achieved using farthest point sampling. n We defer the discussion on n How to select n How to compute ? ? of . 7

Processing and Analysis of Geometric Shapes Discrete Geometry Farthest point sampling Farthest point 8

Processing and Analysis of Geometric Shapes Discrete Geometry Farthest point sampling n Start with some . n Determine sampling radius n If stop. n Find the farthest point from n Add to 9

10 Processing and Analysis of Geometric Shapes Discrete Geometry Farthest point sampling n Outcome: -separated -covering of . n Produces sampling with progressively increasing density. n A greedy algorithm: previously added points remain in n There might be another -separated . -covering containing less points. n In practice used to sub-sample a densely sampled shape. n Straightforward time complexity: number of points in dense sampling, number of points in n Using efficient data structures can be reduced to . .

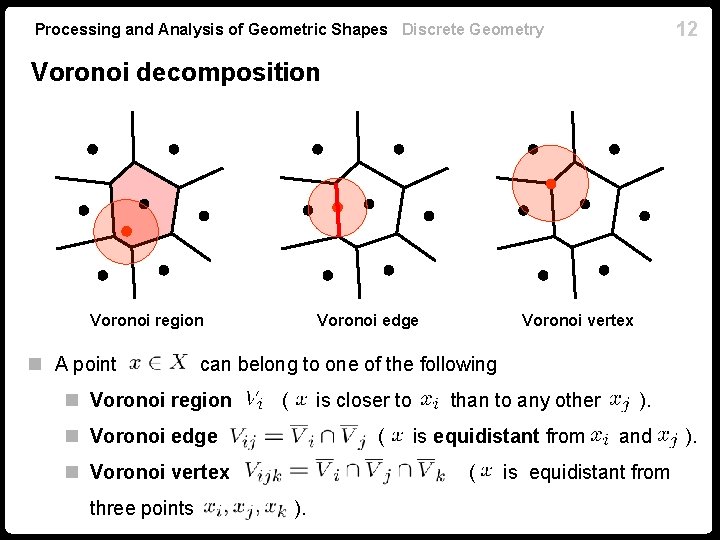
11 Processing and Analysis of Geometric Shapes Discrete Geometry Sampling as representation n Sampling represents a region on as a single point n Region of points on than to any other closer to . n Voronoi region (a. k. a. Dirichlet or Voronoi-Dirichlet region, Thiessen polytope or polygon, Wigner-Seitz zone, domain of action). n To avoid degenerate cases, assume points in in general position: n No three points lie on the same geodesic. (Euclidean case: no three collinear points). n No four points lie on the boundary of the same metric ball. (Euclidean case: no four cocircular points).

12 Processing and Analysis of Geometric Shapes Discrete Geometry Voronoi decomposition Voronoi region n A point Voronoi edge can belong to one of the following n Voronoi region ( is closer to n Voronoi edge ( n Voronoi vertex three points Voronoi vertex than to any other is equidistant from ( ). and is equidistant from ).

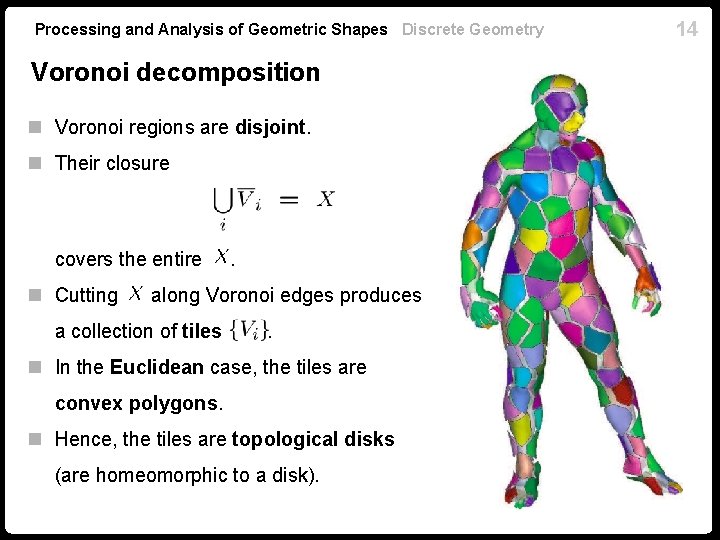
Processing and Analysis of Geometric Shapes Discrete Geometry Voronoi decomposition 13

Processing and Analysis of Geometric Shapes Discrete Geometry Voronoi decomposition n Voronoi regions are disjoint. n Their closure covers the entire n Cutting . along Voronoi edges produces a collection of tiles . n In the Euclidean case, the tiles are convex polygons. n Hence, the tiles are topological disks (are homeomorphic to a disk). 14

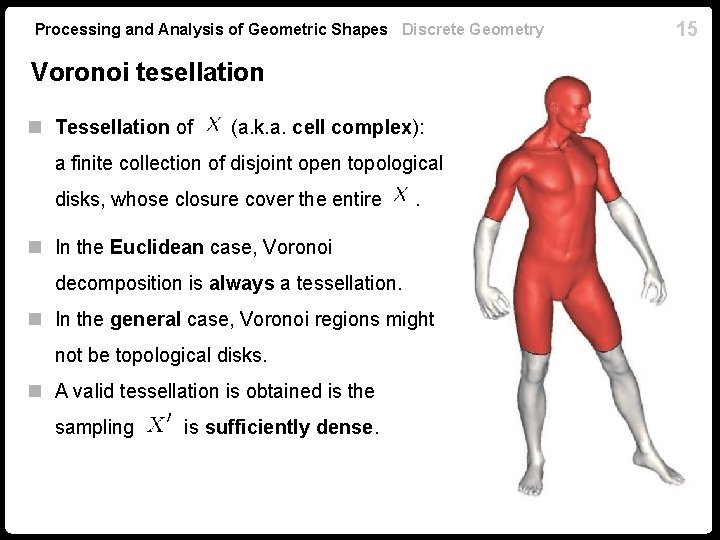
Processing and Analysis of Geometric Shapes Discrete Geometry Voronoi tesellation n Tessellation of (a. k. a. cell complex): a finite collection of disjoint open topological disks, whose closure cover the entire . n In the Euclidean case, Voronoi decomposition is always a tessellation. n In the general case, Voronoi regions might not be topological disks. n A valid tessellation is obtained is the sampling is sufficiently dense. 15

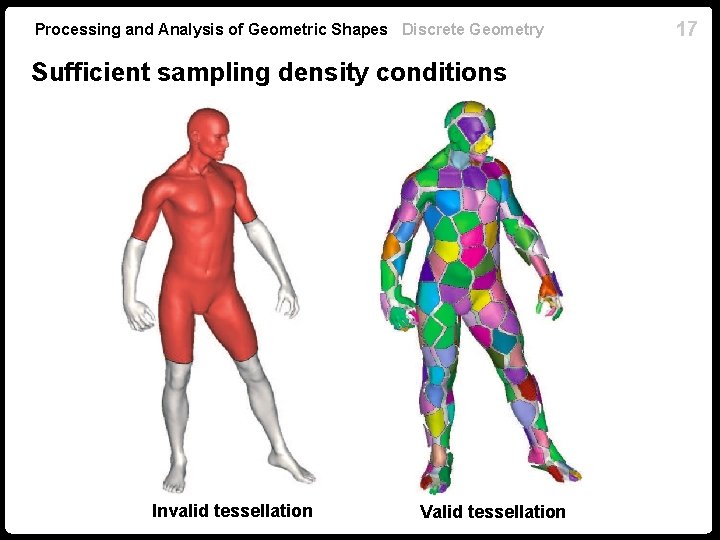
16 Processing and Analysis of Geometric Shapes Discrete Geometry Non-Euclidean Voronoi tessellations n Convexity radius at a point closed ball is the largest is convex in every , i. e. , minimal geodesics between lie in n Convexity radius of for which the . = infimum of convexity radii over all . n Theorem (Leibon & Letscher, 2000): An -separated -covering of with convexity radius of is guaranteed to produce a valid Voronoi tessellation. n Gives sufficient sampling density conditions.

Processing and Analysis of Geometric Shapes Discrete Geometry Sufficient sampling density conditions Invalid tessellation Valid tessellation 17

Processing and Analysis of Geometric Shapes Discrete Geometry Voronoi tessellations in Nature 18

Processing and Analysis of Geometric Shapes Discrete Geometry ® MATLAB intermezzo Farthest point sampling and Voronoi decomposition 19

20 Processing and Analysis of Geometric Shapes Discrete Geometry Representation error n Voronoi decomposition replaces n Mapping copying each with the closest point into n Quantify the representation error introduced by n Let . . be picked randomly with uniform distribution on n Representation error = variance of . .

Processing and Analysis of Geometric Shapes Discrete Geometry 21 Optimal sampling n In the Euclidean case: (mean squared error). n Optimal sampling: given a fixed sampling size Alternatively: Given a fixed representation error size , minimize error , minimize sampling

22 Processing and Analysis of Geometric Shapes Discrete Geometry Centroidal Voronoi tessellation n In a sampling minimizing , each has to satisfy (intrinsic centroid) n In the Euclidean case – center of mass n In general case: intrinsic centroid of . n Centroidal Voronoi tessellation (CVT): Voronoi tessellation generated by in which each is the intrinsic centroid of .

Processing and Analysis of Geometric Shapes Discrete Geometry Lloyd-Max algorithm n Start with some sampling (e. g. , produced by FPS) n Construct Voronoi decomposition n For each , compute intrinsic centroids n Update n In the limit , approaches the hexagonal honeycomb shape – the densest possible tessellation. n Lloyd-Max algorithms is known under many other names: vector quantization, k-means, etc. 23

Processing and Analysis of Geometric Shapes Discrete Geometry 24 Sampling as clustering Partition the space into clusters with centers to minimize some cost function n Maximum cluster radius n Average cluster radius In the discrete setting, both problems are NP-hard Lloyd-Max algorithm, a. k-means is a heuristic, sometimes minimizing average cluster radius (if converges globally – not guaranteed)

Processing and Analysis of Geometric Shapes Discrete Geometry Farthest point sampling encore n Start with some , n For n Find the farthest point n Compute the sampling radius Lemma n. n 25

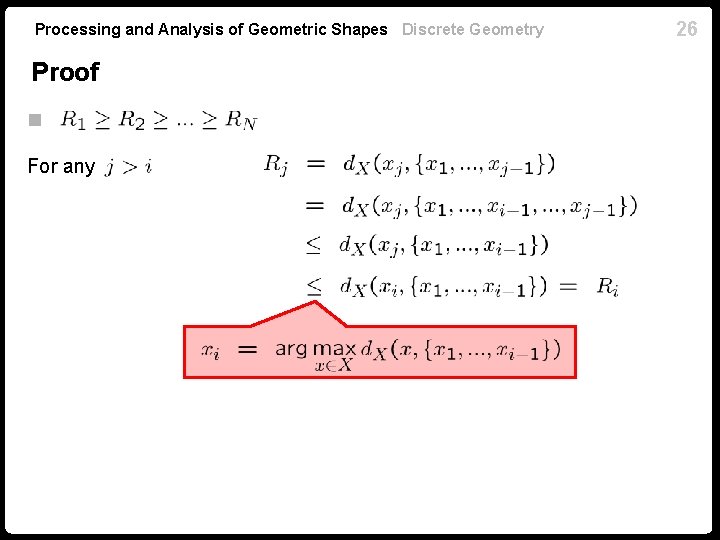
Processing and Analysis of Geometric Shapes Discrete Geometry Proof n For any 26

Processing and Analysis of Geometric Shapes Discrete Geometry Proof (cont) n Since , we have 27

Processing and Analysis of Geometric Shapes Discrete Geometry Almost optimal sampling Theorem (Hochbaum & Shmoys, 1985) Let be the result of the FPS algorithm. Then In other words: FPS is worse than optimal sampling by at most 2. 28

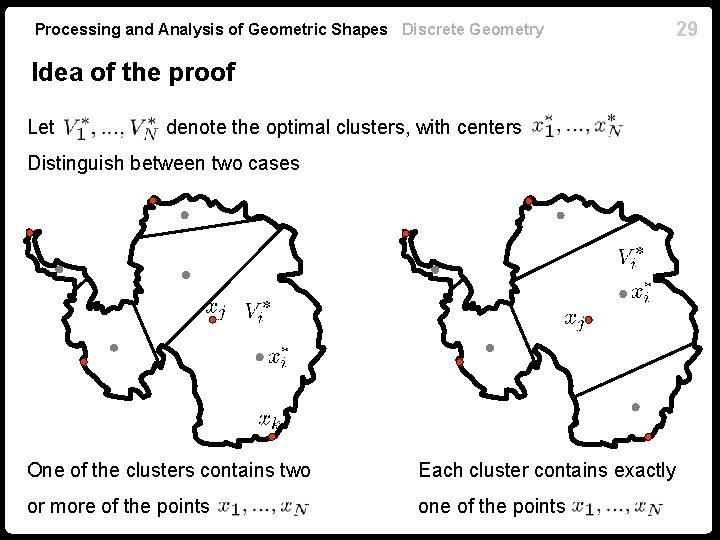
Processing and Analysis of Geometric Shapes Discrete Geometry 29 Idea of the proof Let denote the optimal clusters, with centers Distinguish between two cases One of the clusters contains two Each cluster contains exactly or more of the points one of the points

Processing and Analysis of Geometric Shapes Discrete Geometry Proof (first case) Assume one of the clusters two or more of the points contains , e. g. triangle inequality Hence: 30

Processing and Analysis of Geometric Shapes Discrete Geometry Proof (second case) Assume each of the clusters contains exactly one of the points , e. g. Then, for any point triangle inequality 31

Processing and Analysis of Geometric Shapes Discrete Geometry Proof (second case, cont) We have: for any In particular, for any point 32

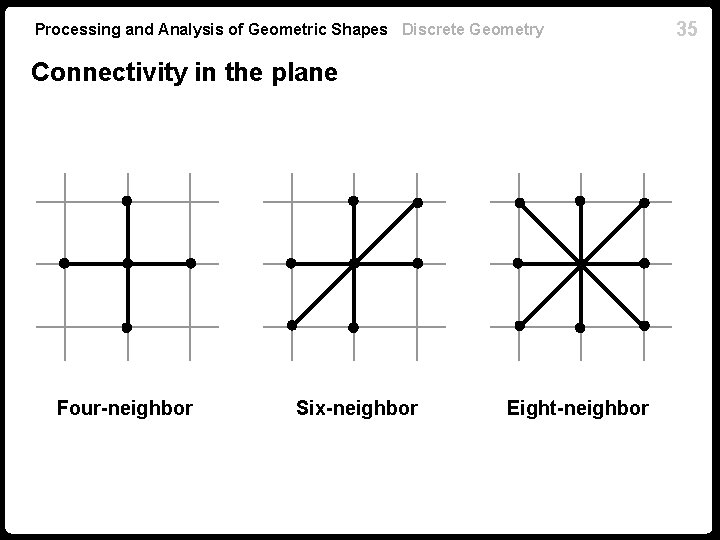
Processing and Analysis of Geometric Shapes Discrete Geometry Connectivity n Neighborhood is a topological definition independent of a metric n Two points are adjacent (directly connected) if they belong to the same neighborhood n The connectivity structure can be represented as an undirected graph with vertices and Vertices Edges edges n Connectivity graph can be represented as a matrix 33

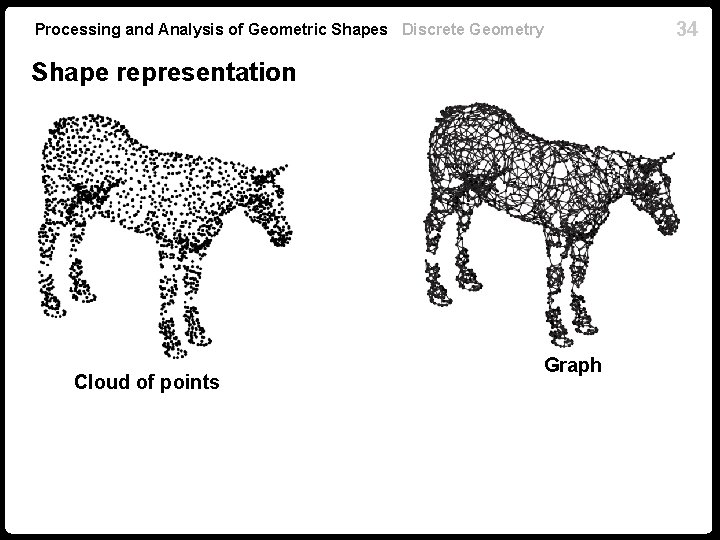
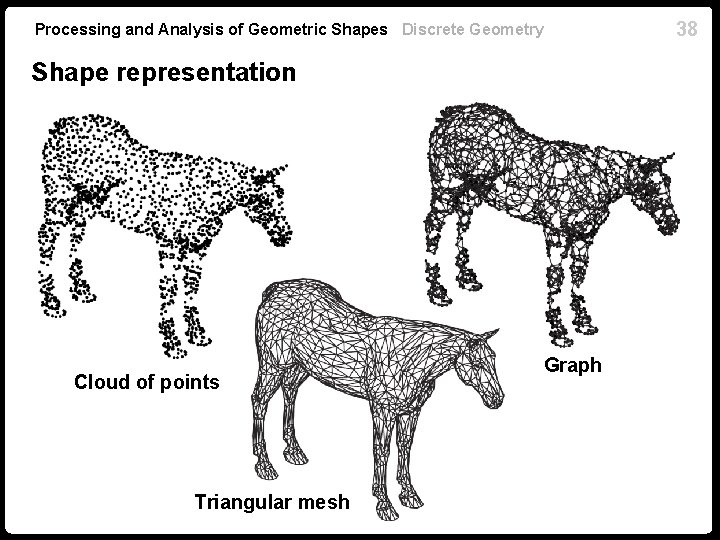
Processing and Analysis of Geometric Shapes Discrete Geometry Shape representation Cloud of points Graph 34

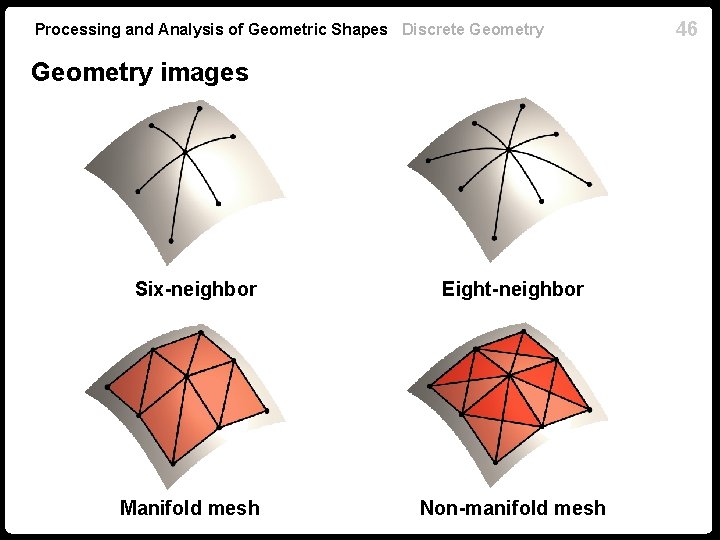
Processing and Analysis of Geometric Shapes Discrete Geometry Connectivity in the plane Four-neighbor Six-neighbor Eight-neighbor 35

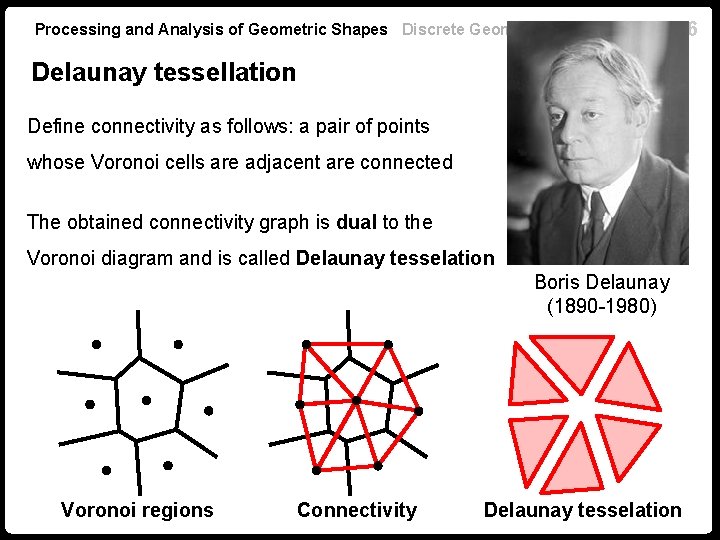
Processing and Analysis of Geometric Shapes Discrete Geometry 36 Delaunay tessellation Define connectivity as follows: a pair of points whose Voronoi cells are adjacent are connected The obtained connectivity graph is dual to the Voronoi diagram and is called Delaunay tesselation Boris Delaunay (1890 -1980) Voronoi regions Connectivity Delaunay tesselation

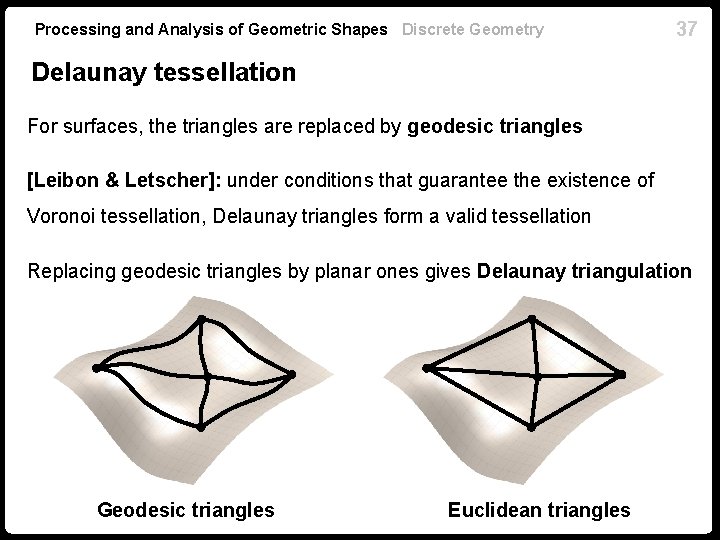
Processing and Analysis of Geometric Shapes Discrete Geometry 37 Delaunay tessellation For surfaces, the triangles are replaced by geodesic triangles [Leibon & Letscher]: under conditions that guarantee the existence of Voronoi tessellation, Delaunay triangles form a valid tessellation Replacing geodesic triangles by planar ones gives Delaunay triangulation Geodesic triangles Euclidean triangles

Processing and Analysis of Geometric Shapes Discrete Geometry Shape representation Cloud of points Triangular mesh Graph 38

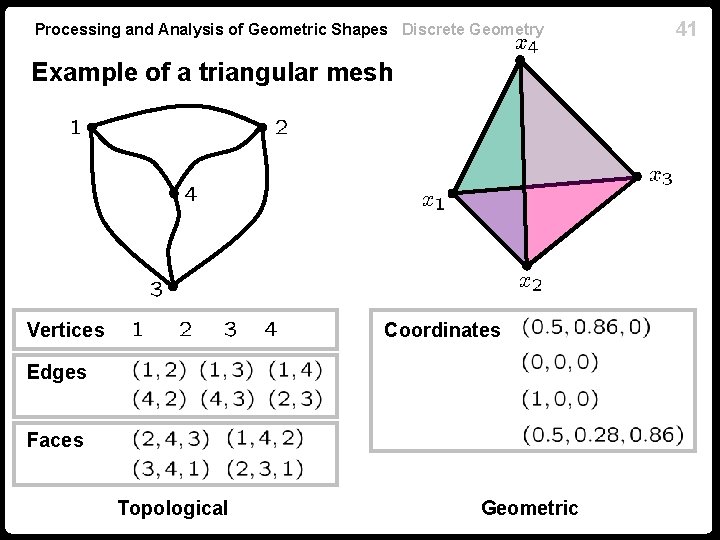
Processing and Analysis of Geometric Shapes Discrete Geometry 39 Triangular meshes A structure of the form consisting of n Vertices n Edges n Faces is called a triangular mesh The mesh is a purely topological object and does not contain any geometric properties The faces can be represented as an row is a vector of the form matrix of indices, where each , and

Processing and Analysis of Geometric Shapes Discrete Geometry Triangular meshes The geometric realization of the mesh is defined by specifying the coordinates of the vertices for all The coordinates can be represented as an matrix The mesh is a piece-wise planar approximation obtained by gluing the triangular faces together, Triangular face 40

Processing and Analysis of Geometric Shapes Discrete Geometry Example of a triangular mesh Vertices Coordinates Edges Faces Topological Geometric 41

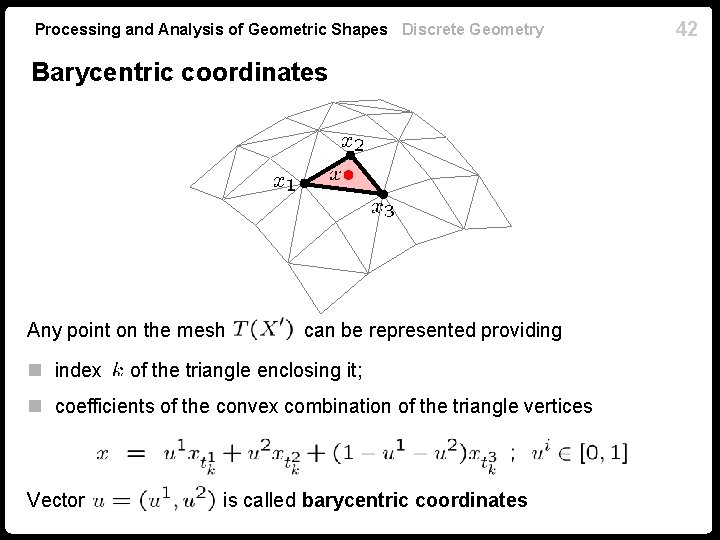
Processing and Analysis of Geometric Shapes Discrete Geometry Barycentric coordinates Any point on the mesh n index can be represented providing of the triangle enclosing it; n coefficients of the convex combination of the triangle vertices Vector is called barycentric coordinates 42

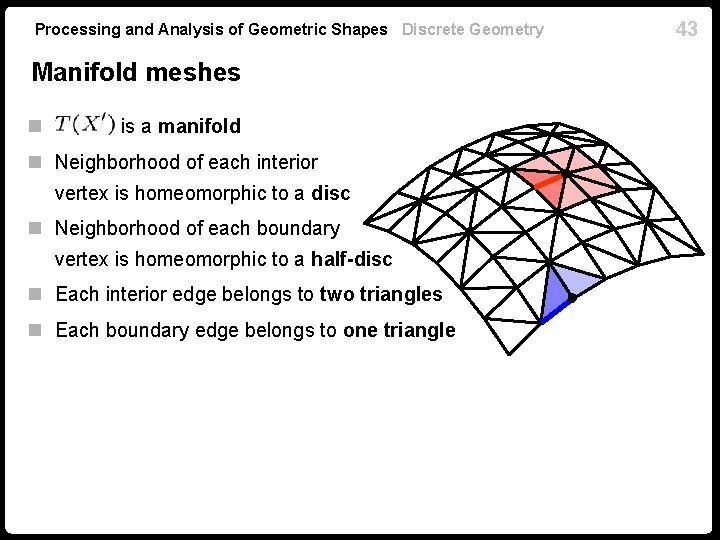
Processing and Analysis of Geometric Shapes Discrete Geometry Manifold meshes n is a manifold n Neighborhood of each interior vertex is homeomorphic to a disc n Neighborhood of each boundary vertex is homeomorphic to a half-disc n Each interior edge belongs to two triangles n Each boundary edge belongs to one triangle 43

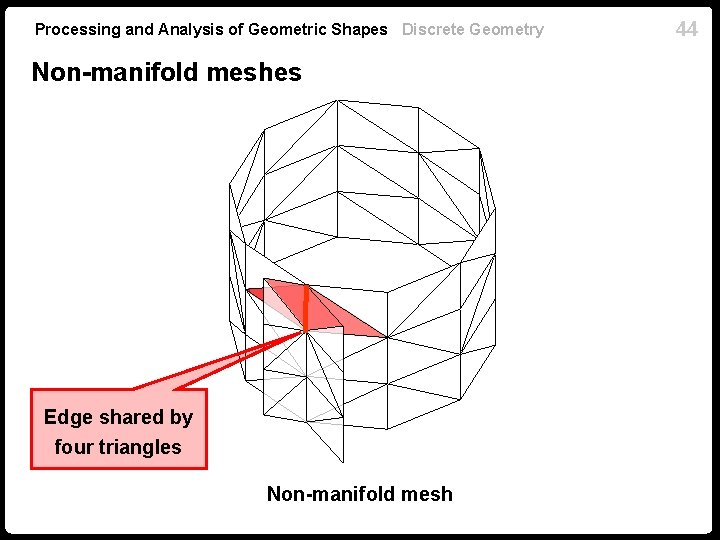
Processing and Analysis of Geometric Shapes Discrete Geometry Non-manifold meshes Edge shared by four triangles Non-manifold mesh 44

Processing and Analysis of Geometric Shapes Discrete Geometry images Surface Geometry image Global parametrization Sampling of parametrization domain on a Cartesian grid 45

Processing and Analysis of Geometric Shapes Discrete Geometry images Six-neighbor Eight-neighbor Manifold mesh Non-manifold mesh 46

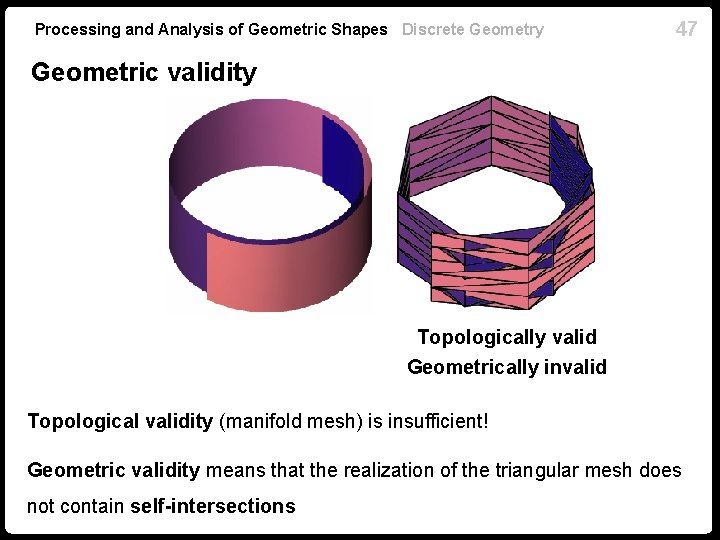
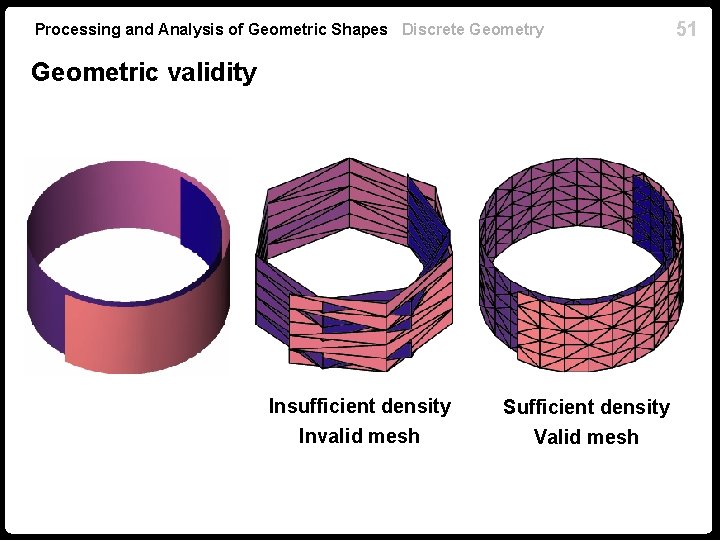
Processing and Analysis of Geometric Shapes Discrete Geometry 47 Geometric validity Topologically valid Geometrically invalid Topological validity (manifold mesh) is insufficient! Geometric validity means that the realization of the triangular mesh does not contain self-intersections

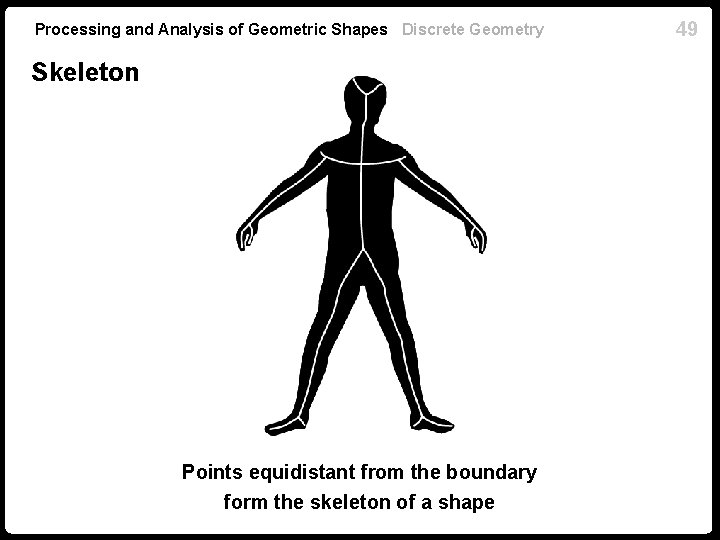
Processing and Analysis of Geometric Shapes Discrete Geometry 48 Skeleton For a smooth compact surface containing , there exists an envelope ) such that every point is continuously mappable to a unique point on The mapping is realized as the closest point on from Problem when is equidistant from two points on (such points are called medial axis or skeleton of If the mesh is contained in the envelope (does not intersect the medial axis), it is valid (open set in )

Processing and Analysis of Geometric Shapes Discrete Geometry Skeleton Points equidistant from the boundary form the skeleton of a shape 49

50 Processing and Analysis of Geometric Shapes Discrete Geometry Local feature size Distance from point on to the medial axis of is called the local feature size, denoted Local feature size related to curvature (not an intrinsic property!) [Amenta&Bern, Leibon&Letscher]: if the surface is sampled such that for every that an open ball of radius contains a point of , it is guaranteed does not intersect the medial axis of Conclusion: there exists sufficiently dense sampling guaranteeing that is geometrically valid

Processing and Analysis of Geometric Shapes Discrete Geometry Geometric validity Insufficient density Invalid mesh Sufficient density Valid mesh 51