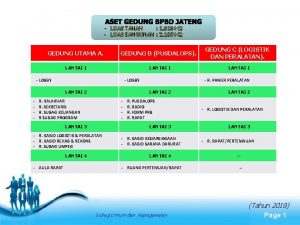
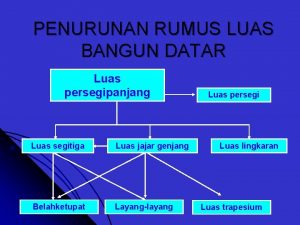
PERTEMUAN 13 ANTI TURUNAN PENDAHULUAN LUAS NOTASI SIGMA

PERTEMUAN 13 ANTI TURUNAN, PENDAHULUAN LUAS & NOTASI SIGMA

Fungsi F disebut anti-turunan f pada I apabila F’(x) = f(x)untuk setiap x є I. Sebagai contoh, F(x) = x 4 + 1 adalah anti-turunan f(x) = 4 x 3 pada R. Secara umum, keluarga fungsi F(x) = x 4 + C merupakan anti-turunan f(x) = 4 x 3 pada R, karena F’(x) = 4 x 3 = f(x) untuk setiap x є R. Keluarga fungsi anti-turunan f(x) disebut integral tak tentu dari f(x), dan dilambangkan dengan ∫ f(x) dx. Jadi, sebagai contoh, ∫ 4 x 3 dx = x 4 + C.

Secara grafik, keluarga fungsi antiturunan f(x) adalah keluarga fungsi yang anggotanya merupakan pergeseran ke atas atau ke bawah dari anggota lainnya. Semua anggota keluarga fungsi tersebut mempunyai turunan yang sama, yaitu f(x)

Persamaan Diferensial Sederhana Jika F’(x) = f(x), maka ∫ f(x) dx = F(x) + dalambahasa diferensial: jika F’(x) = f(x), maka d. F(x) = F’(x) dx = f(x) dx (*) sehingga ∫ d. F(x) = ∫ f(x) dx = F(x) + C. Persamaan (*) merupakan contoh persamaan diferensial yang (paling) sederhana.

NOTASI SIGMA Penjumlahan deret n bilangan a 1 + a 2 + … + an dilambangkan dengan notasi sigma

TEOREMA KELINIERAN DAN SIGMA KHUSUS o o Teorema Kelinieran Beberapa deret khusus (dengan indeks i berjalan dari 1 sampai dengan n), di antaranya:

Deret pertama merupakan deret aritmetika n bilangandengan suku pertama 1 dan beda 1. Untuk pembuktian rumus deret lihat Purcell

LUAS DAERAH DAN JUMLAH RIEMANN

Jumlah Riemann

Perenungan Selanjutnya dapat direnungkan bahwa pendefinisian integral tentu dalam mencari luas daerah adalah sama dengan mencari limit jumlah Riemannya

Latihan o o Ambil beberapa fungsi sederhana yaitu fungsi linier atau kuadrat, dengan batas yang ditentukan Tentukan Luas Daerah dengan partisi dan menggunakan limit Jumlah Riemann Agak sedikit loncat. . selesaikan fungsi dan batas tertentu tadi dengan integral tentu dan bandingkan dengan hasil limit jumlah Riemann Presentasikan setiap kelompok…Apa yang dapat ditealaah

PERTEMUAN 14 INTEGRAL TAK TENTU DAN TENTU (SUATU PENDAHULUAN)

Integral tak tentu o o Mengintegralkan suatu fungsi turunan f(x) berarti adalah mencari integral atau turunan antinya, yaitu F(x) Bentuk umum integral dari f(x) adalah : Dimana k adalah sembarang konstanta yang nilainya tidak tentu. 15

Integral tak tentu © o Contoh untuk fungsi asal : F(x) = x 2 + 5 fungsi turunannya : f(x) = d. F(x) / dx = 2 x Jika prosesnya dibalik, maka : 16

Kaidah- kaidah Integrasi tak tentu Kaidah 1. Formula Pangkat Kaidah 2. Formula Logaritmis 17

Kaidah- kaidah Integrasi tak tentu © o Kaidah 3. Formula Eksponensial o Kaidah 4. Formula Penjumlahan 18

Kaidah-kaidah Integrasi tak tentu © o Kaidah 5. Formula Perkalian o Kaidah 6. Formula Substitusi 19

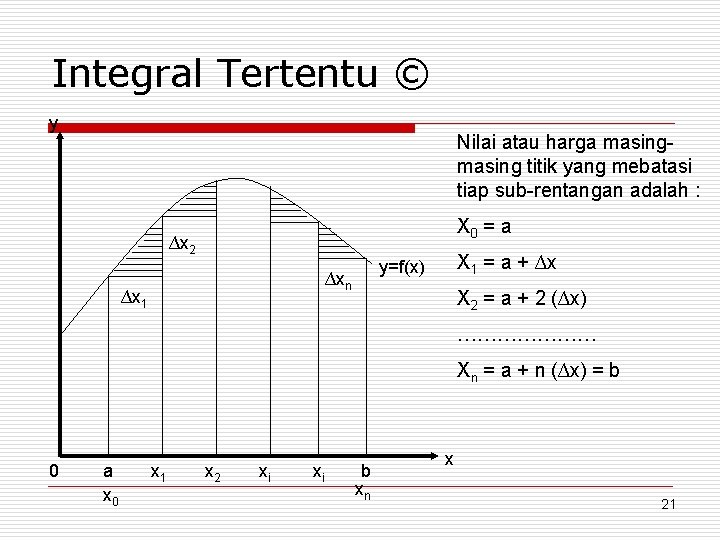
Integral Tertentu o o o Integral tertentu adalah integral dari suatu fungsi yang nilai-nilai variabel bebasnya (memiliki batas-batas) tertentu. Integral tertentu digunakan untuk menghitung luas areal yang terletak di antara kurva y = f(x) dan sumbu horizontal – x, dalam suatu rentangan wilayah yang dibatasi oleh x = a dan x =b. Bentuk umum : 20

Integral Tertentu © y Nilai atau harga masing titik yang mebatasi tiap sub-rentangan adalah : X 0 = a ∆x 2 ∆xn ∆x 1 X 1 = a + ∆x y=f(x) X 2 = a + 2 (∆x) ………………… Xn = a + n (∆x) = b 0 a x 0 x 1 x 2 xi xi b xn x 21

Kaidah- kaidah Integrasi Tertentu Untuk a < b < c, berlaku : 22

Kaidah- kaidah Integrasi Tertentu © 23

Latihan o Evaluasi integral dibawah ini 24