Operations Management Supplement 6 Statistical Process Control Power

Operations Management Supplement 6 – Statistical Process Control Power. Point presentation to accompany Heizer/Render Principles of Operations Management, 6 e Operations Management, 8 e © 2006 Prentice Hall, Inc. © 2006 Prentice S 6 –

Outline þ Statistical Process Control (SPC) þ Control Charts for Variables þ The Central Limit Theorem þ Setting Mean Chart Limits (x-Charts) þ Setting Range Chart Limits (R-Charts) þ Using Mean and Range Charts þ Control Charts for Attributes þ Managerial Issues and Control Charts © 2006 Prentice Hall, Inc. S 6 –

Outline – Continued þ Process Capability Ratio (Cp) þ Process Capability Index (Cpk ) þ Acceptance Sampling þ Operating Characteristic Curve þ Average Outgoing Quality © 2006 Prentice Hall, Inc. S 6 –

Learning Objectives When you complete this supplement, you should be able to: Identify or Define: þ Natural and assignable causes of variation þ Central limit theorem þ Attribute and variable inspection þ Process control þ x-charts and R-charts © 2006 Prentice Hall, Inc. S 6 –

Learning Objectives When you complete this supplement, you should be able to: Identify or Define: þ þ þ © 2006 Prentice Hall, Inc. LCL and UCL P-charts and c-charts Cp and Cpk Acceptance sampling OC curve S 6 –

Learning Objectives When you complete this supplement, you should be able to: Identify or Define: þ AQL and LTPD þ AOQ þ Producer’s and consumer’s risk © 2006 Prentice Hall, Inc. S 6 –

Learning Objectives When you complete this supplement, you should be able to: Describe or Explain: þ The role of statistical quality control © 2006 Prentice Hall, Inc. S 6 –

Statistical Process Control (SPC) þ Variability is inherent in every process þ Natural or common causes þ Special or assignable causes þ Provides a statistical signal when assignable causes are present þ Detect and eliminate assignable causes of variation © 2006 Prentice Hall, Inc. S 6 –

Natural Variations þ Also called common causes þ Affect virtually all production processes þ Expected amount of variation þ Output measures follow a probability distribution þ For any distribution there is a measure of central tendency and dispersion þ If the distribution of outputs falls within acceptable limits, the process is said to be “in control” © 2006 Prentice Hall, Inc. S 6 – 9

Assignable Variations þ Also called special causes of variation þ Generally this is some change in the process þ Variations that can be traced to a specific reason þ The objective is to discover when assignable causes are present þ Eliminate the bad causes þ Incorporate the good causes © 2006 Prentice Hall, Inc. S 6 – 10

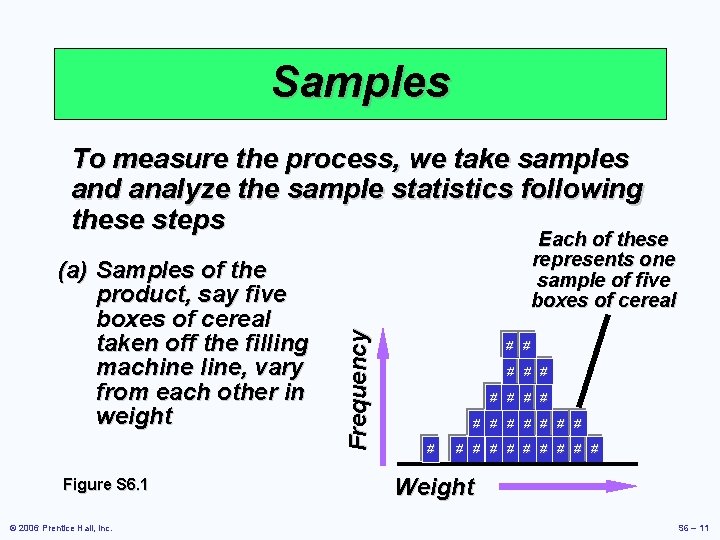
Samples To measure the process, we take samples and analyze the sample statistics following these steps Figure S 6. 1 © 2006 Prentice Hall, Inc. Frequency (a) Samples of the product, say five boxes of cereal taken off the filling machine line, vary from each other in weight Each of these represents one sample of five boxes of cereal # # # # # # # Weight S 6 – 11

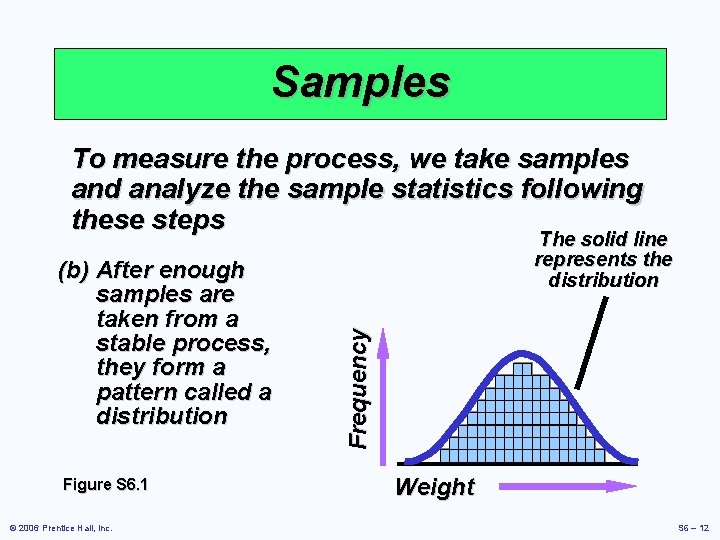
Samples To measure the process, we take samples and analyze the sample statistics following these steps Figure S 6. 1 © 2006 Prentice Hall, Inc. Frequency (b) After enough samples are taken from a stable process, they form a pattern called a distribution The solid line represents the distribution Weight S 6 – 12

Samples To measure the process, we take samples and analyze the sample statistics following these steps Frequency (c) There are many types of distributions, including the normal (bell-shaped) distribution, but distributions do differ in terms of central tendency (mean), standard deviation or variance, and shape Figure S 6. 1 Central tendency Weight © 2006 Prentice Hall, Inc. Variation Weight Shape Weight S 6 – 13

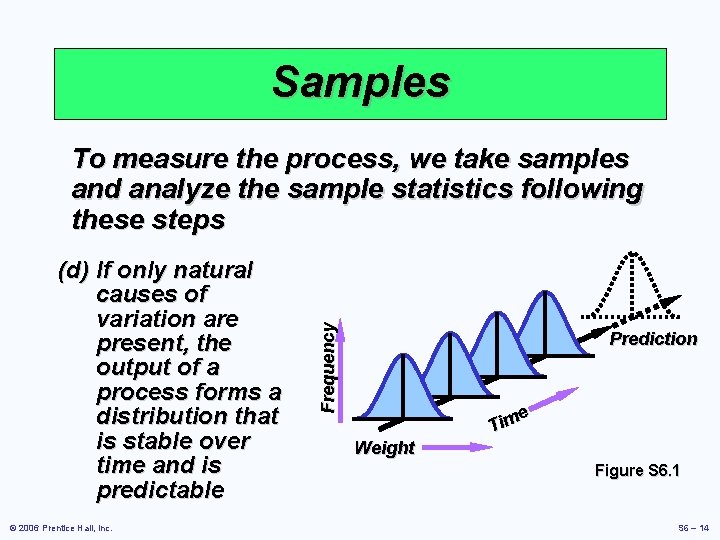
Samples (d) If only natural causes of variation are present, the output of a process forms a distribution that is stable over time and is predictable © 2006 Prentice Hall, Inc. Frequency To measure the process, we take samples and analyze the sample statistics following these steps Prediction e m i T Weight Figure S 6. 1 S 6 – 14

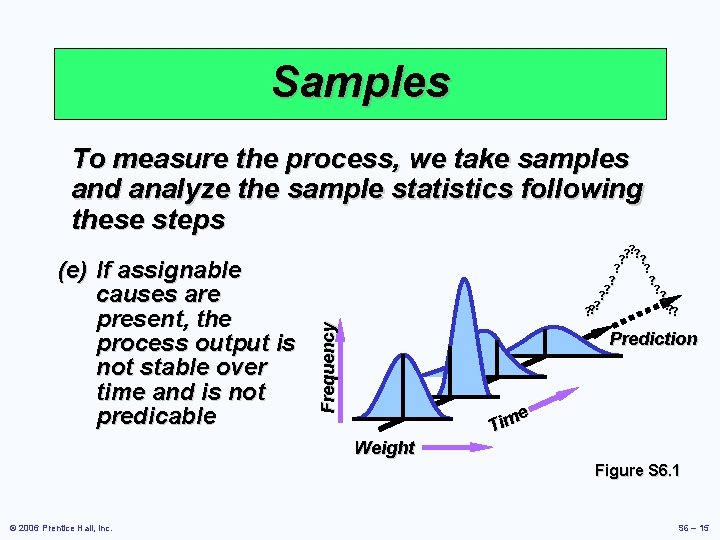
Samples To measure the process, we take samples and analyze the sample statistics following these steps Frequency (e) If assignable causes are present, the process output is not stable over time and is not predicable ? ? ? ? ? Prediction e m i T Weight Figure S 6. 1 © 2006 Prentice Hall, Inc. S 6 – 15

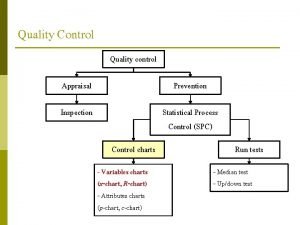
Control Charts Constructed from historical data, the purpose of control charts is to help distinguish between natural variations and variations due to assignable causes © 2006 Prentice Hall, Inc. S 6 –

Types of Data Variables þ Characteristics that can take any real value þ May be in whole or in fractional numbers þ Continuous random variables © 2006 Prentice Hall, Inc. Attributes þ Defect-related characteristics þ Classify products as either good or bad or count defects þ Categorical or discrete random variables S 6 – 17

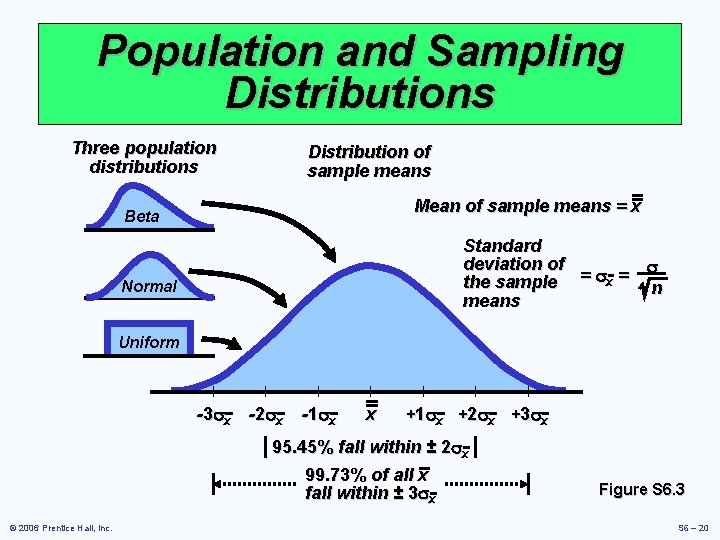
Central Limit Theorem Regardless of the distribution of the population, the distribution of sample means drawn from the population will tend to follow a normal curve 1. The mean of the sampling distribution (x) will be the same as the population mean m 2. The standard deviation of the sampling distribution (sx) will equal the population standard deviation (s) divided by the square root of the sample size, n © 2006 Prentice Hall, Inc. x=m sx = s n S 6 –

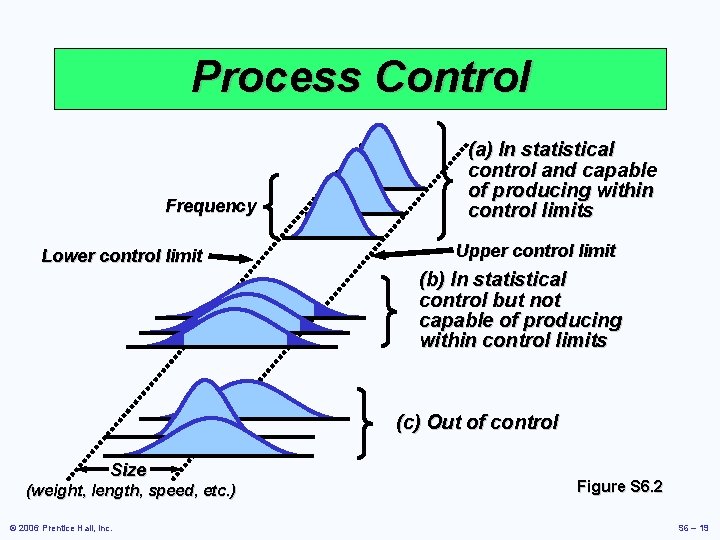
Process Control Frequency Lower control limit (a) In statistical control and capable of producing within control limits Upper control limit (b) In statistical control but not capable of producing within control limits (c) Out of control Size (weight, length, speed, etc. ) © 2006 Prentice Hall, Inc. Figure S 6. 2 S 6 – 19

Population and Sampling Distributions Three population distributions Distribution of sample means Mean of sample means = x Beta Standard deviation of s = x the sample n means Normal Uniform | | -3 s x -2 s x -1 s x x | | + 1 sx + 2 sx + 3 sx 95. 45% fall within ± 2 sx 99. 73% of all x fall within ± 3 sx © 2006 Prentice Hall, Inc. | Figure S 6. 3 S 6 – 20

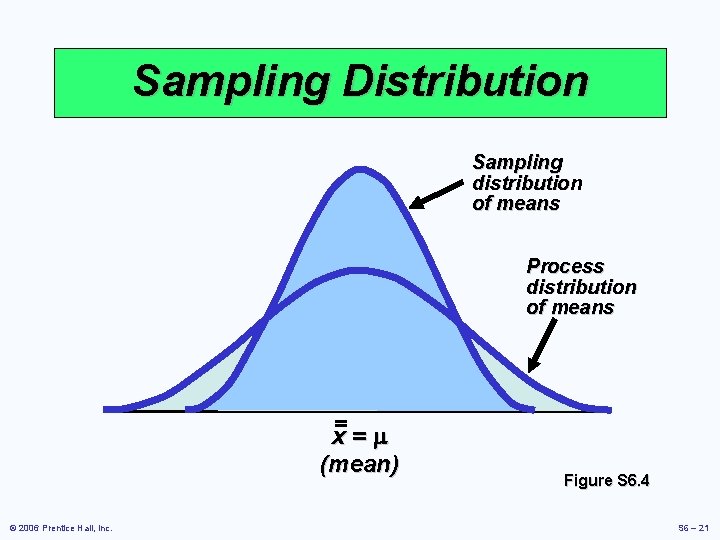
Sampling Distribution Sampling distribution of means Process distribution of means x=m (mean) © 2006 Prentice Hall, Inc. Figure S 6. 4 S 6 – 21

Steps In Creating Control Charts 1. Take samples from the population and compute the appropriate sample statistic 2. Use the sample statistic to calculate control limits and draw the control chart 3. Plot sample results on the control chart and determine the state of the process (in or out of control) 4. Investigate possible assignable causes and take any indicated actions 5. Continue sampling from the process and reset the control limits when necessary © 2006 Prentice Hall, Inc. S 6 – 22

Control Charts for Variables þ For variables that have continuous dimensions þ Weight, speed, length, strength, etc. þ x-charts are to control the central tendency of the process þ R-charts are to control the dispersion of the process þ These two charts must be used together © 2006 Prentice Hall, Inc. S 6 –

Setting Chart Limits For x-Charts when we know s Upper control limit (UCL) = x + zsx Lower control limit (LCL) = x - zsx where © 2006 Prentice Hall, Inc. x =mean of the sample means or a target value set for the process z =number of normal standard deviations sx =standard deviation of the sample means = s/ n s =population standard deviation n =sample size S 6 – 24

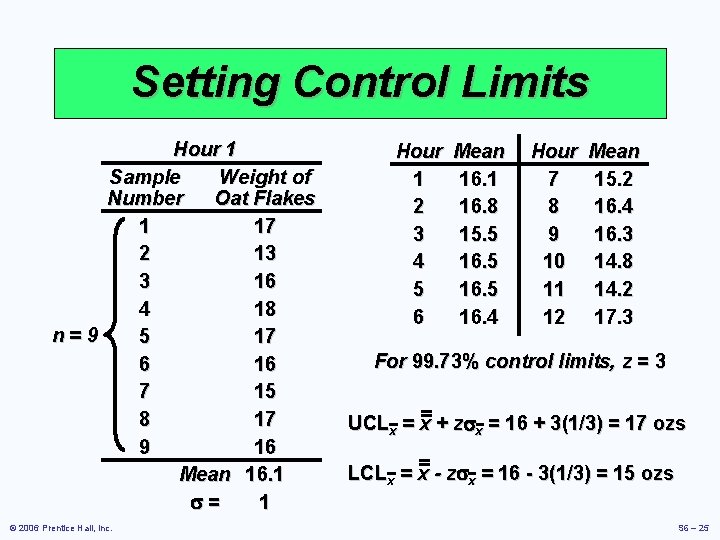
Setting Control Limits Hour 1 Sample Weight of Number Oat Flakes 1 17 2 13 3 16 4 18 n=9 5 17 6 16 7 15 8 17 9 16 Mean 16. 1 s= 1 © 2006 Prentice Hall, Inc. Hour 1 2 3 4 5 6 Mean 16. 1 16. 8 15. 5 16. 4 Hour 7 8 9 10 11 12 Mean 15. 2 16. 4 16. 3 14. 8 14. 2 17. 3 For 99. 73% control limits, z = 3 UCLx = x + zsx = 16 + 3(1/3) = 17 ozs LCLx = x - zsx = 16 - 3(1/3) = 15 ozs S 6 – 25

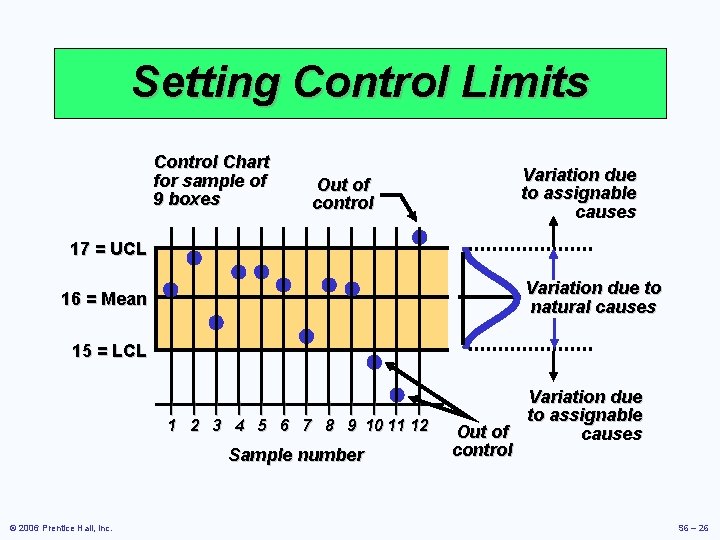
Setting Control Limits Control Chart for sample of 9 boxes Out of control Variation due to assignable causes 17 = UCL Variation due to natural causes 16 = Mean 15 = LCL | | | 1 2 3 4 5 6 7 8 9 10 11 12 Sample number © 2006 Prentice Hall, Inc. Variation due to assignable Out of causes control S 6 – 26

Setting Chart Limits For x-Charts when we don’t know s Upper control limit (UCL) = x + A 2 R Lower control limit (LCL) = x - A 2 R where © 2006 Prentice Hall, Inc. R A 2 x =average range of the samples =control chart factor found in Table S 6. 1 =mean of the sample means S 6 – 27

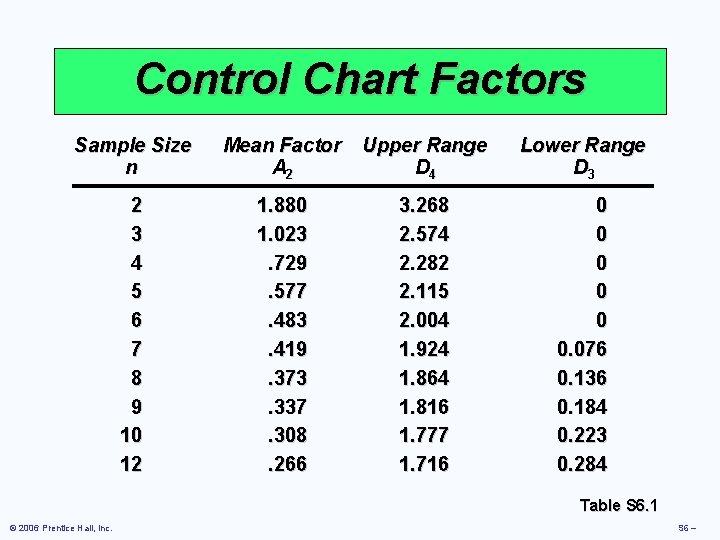
Control Chart Factors Sample Size n Mean Factor A 2 Upper Range D 4 Lower Range D 3 2 3 4 5 6 7 8 9 10 12 1. 880 1. 023. 729. 577. 483. 419. 373. 337. 308. 266 3. 268 2. 574 2. 282 2. 115 2. 004 1. 924 1. 864 1. 816 1. 777 1. 716 0 0 0. 076 0. 136 0. 184 0. 223 0. 284 Table S 6. 1 © 2006 Prentice Hall, Inc. S 6 –

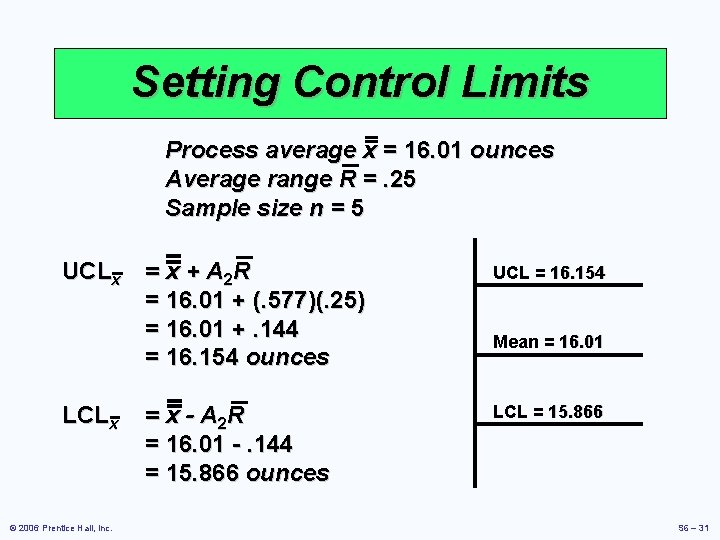
Setting Control Limits Process average x = 16. 01 ounces Average range R =. 25 Sample size n = 5 © 2006 Prentice Hall, Inc. S 6 – 29

Setting Control Limits Process average x = 16. 01 ounces Average range R =. 25 Sample size n = 5 UCLx © 2006 Prentice Hall, Inc. = x + A 2 R = 16. 01 + (. 577)(. 25) = 16. 01 +. 144 = 16. 154 ounces From Table S 6. 1 S 6 – 30

Setting Control Limits Process average x = 16. 01 ounces Average range R =. 25 Sample size n = 5 UCLx LCLx © 2006 Prentice Hall, Inc. = x + A 2 R = 16. 01 + (. 577)(. 25) = 16. 01 +. 144 = 16. 154 ounces UCL = 16. 154 = x - A 2 R = 16. 01 -. 144 = 15. 866 ounces LCL = 15. 866 Mean = 16. 01 S 6 – 31

R – Chart þ Type of variables control chart þ Shows sample ranges over time þ Difference between smallest and largest values in sample þ Monitors process variability þ Independent from process mean © 2006 Prentice Hall, Inc. S 6 –

Setting Chart Limits For R-Charts Upper control limit (UCLR) = D 4 R Lower control limit (LCLR) = D 3 R where R =average range of the samples D 3 and D 4 =control chart factors from Table S 6. 1 © 2006 Prentice Hall, Inc. S 6 – 33

Setting Control Limits Average range R = 5. 3 pounds Sample size n = 5 From Table S 6. 1 D 4 = 2. 115, D 3 = 0 UCLR = D 4 R = (2. 115)(5. 3) = 11. 2 pounds UCL = 11. 2 LCLR LCL = 0 © 2006 Prentice Hall, Inc. = D 3 R = (0)(5. 3) = 0 pounds Mean = 5. 3 S 6 – 34

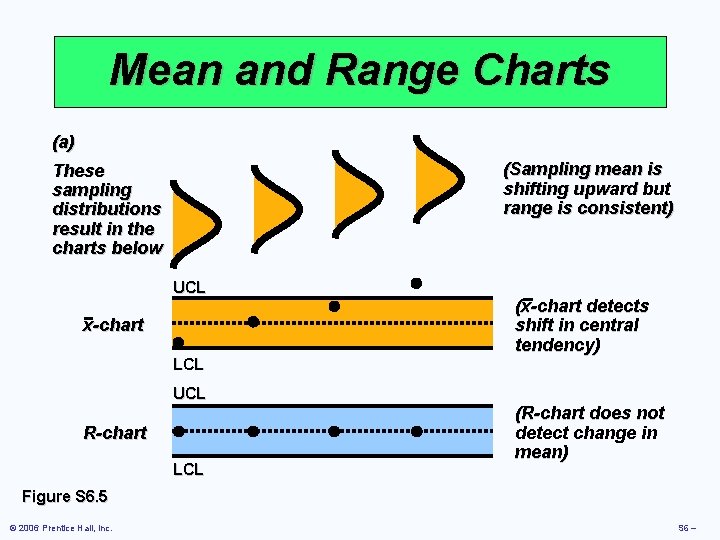
Mean and Range Charts (a) (Sampling mean is shifting upward but range is consistent) These sampling distributions result in the charts below UCL x-chart LCL UCL R-chart LCL (x-chart detects shift in central tendency) (R-chart does not detect change in mean) Figure S 6. 5 © 2006 Prentice Hall, Inc. S 6 –

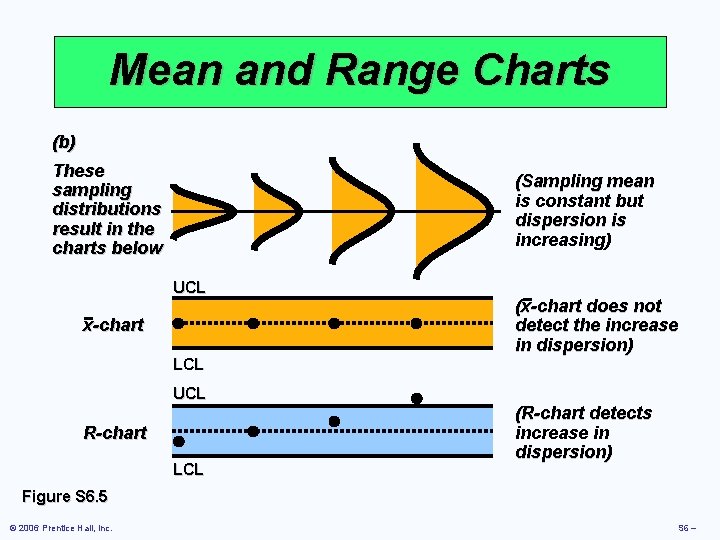
Mean and Range Charts (b) These sampling distributions result in the charts below (Sampling mean is constant but dispersion is increasing) UCL x-chart LCL UCL R-chart LCL (x-chart does not detect the increase in dispersion) (R-chart detects increase in dispersion) Figure S 6. 5 © 2006 Prentice Hall, Inc. S 6 –

Automated Control Charts © 2006 Prentice Hall, Inc. S 6 –

Control Charts for Attributes þ For variables that are categorical þ Good/bad, yes/no, acceptable/unacceptable þ Measurement is typically counting defectives þ Charts may measure þ Percent defective (p-chart) þ Number of defects (c-chart) © 2006 Prentice Hall, Inc. S 6 –

Control Limits for p-Charts Population will be a binomial distribution, but applying the Central Limit Theorem allows us to assume a normal distribution for the sample statistics UCLp = p + zsp^ sp = ^ LCLp = p - zsp^ where © 2006 Prentice Hall, Inc. p z sp^ n p(1 - p) n =mean fraction defective in the sample =number of standard deviations =standard deviation of the sampling distribution =sample size S 6 – 39

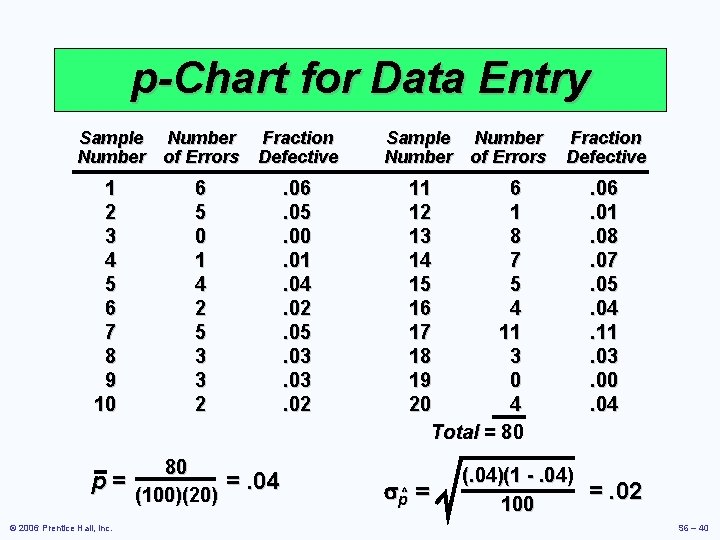
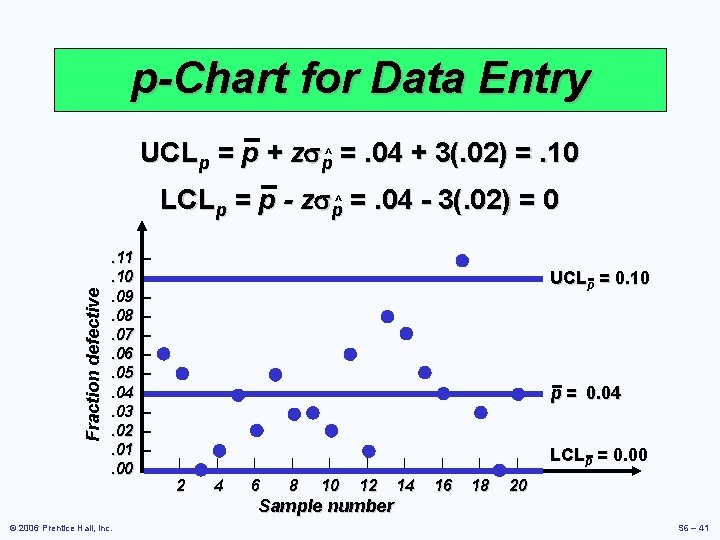
p-Chart for Data Entry Sample Number of Errors 1 2 3 4 5 6 7 8 9 10 p= © 2006 Prentice Hall, Inc. Fraction Defective Sample Number of Errors Fraction Defective . 06. 05. 00. 01. 04. 02. 05. 03. 02 11 6 12 1 13 8 14 7 15 5 16 4 17 11 18 3 19 0 20 4 Total = 80 . 06. 01. 08. 07. 05. 04. 11. 03. 00. 04 6 5 0 1 4 2 5 3 3 2 80 (100)(20) =. 04 sp^ = (. 04)(1 -. 04) 100 =. 02 S 6 – 40

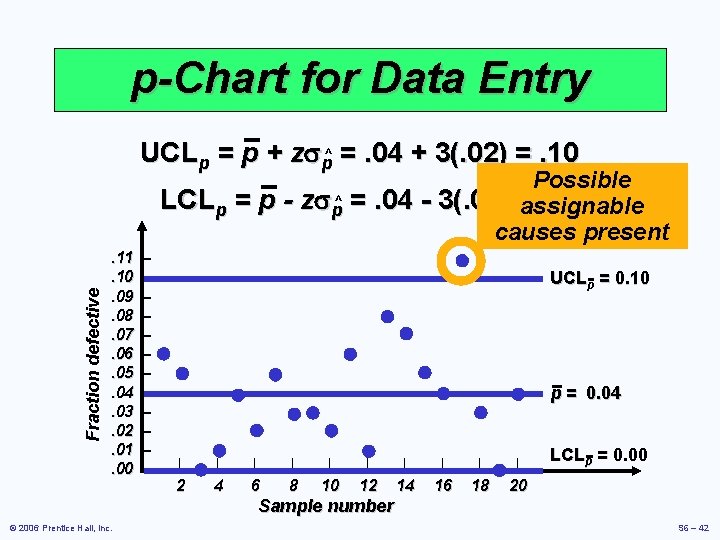
p-Chart for Data Entry UCLp = p + zsp^ =. 04 + 3(. 02) =. 10 Fraction defective LCLp = p - zsp^ =. 04 - 3(. 02) = 0. 11. 10. 09. 08. 07. 06. 05. 04. 03. 02. 01. 00 – – – UCLp = 0. 10 p = 0. 04 | | | | | 2 4 6 8 10 12 14 16 18 20 LCLp = 0. 00 Sample number © 2006 Prentice Hall, Inc. S 6 – 41

p-Chart for Data Entry UCLp = p + zsp^ =. 04 + 3(. 02) =. 10 Fraction defective Possible LCLp = p - zsp^ =. 04 - 3(. 02) = 0 assignable causes present . 11. 10. 09. 08. 07. 06. 05. 04. 03. 02. 01. 00 – – – UCLp = 0. 10 p = 0. 04 | | | | | 2 4 6 8 10 12 14 16 18 20 LCLp = 0. 00 Sample number © 2006 Prentice Hall, Inc. S 6 – 42

Control Limits for c-Charts Population will be a Poisson distribution, but applying the Central Limit Theorem allows us to assume a normal distribution for the sample statistics UCLc = c + 3 c where © 2006 Prentice Hall, Inc. LCLc = c - 3 c c =mean number defective in the sample S 6 – 43

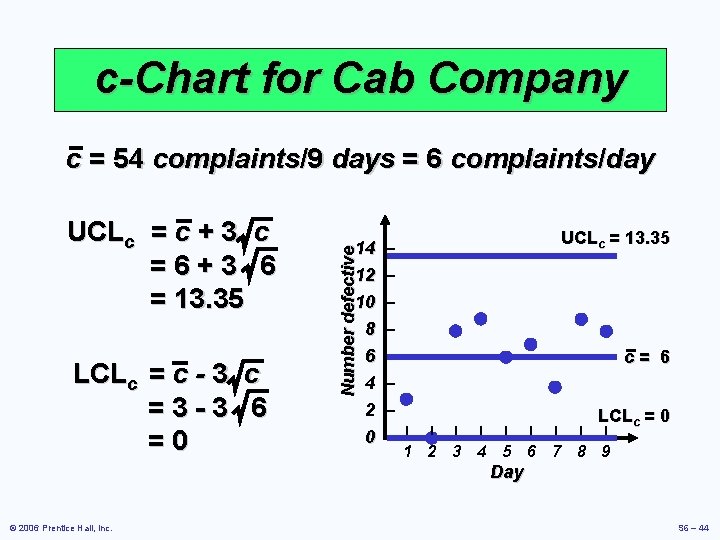
c-Chart for Cab Company c = 54 complaints/9 days = 6 complaints/day LCLc = c - 3 c =3 -3 6 =0 UCLc = 13. 35 14 14 – 12 – 10 – Number defective UCLc = c + 3 c =6+3 6 = 13. 35 8 6 4 2 0 – – – | c= 6 LCLc = 0 | | | | 1 2 3 4 5 6 7 8 9 Day © 2006 Prentice Hall, Inc. S 6 – 44

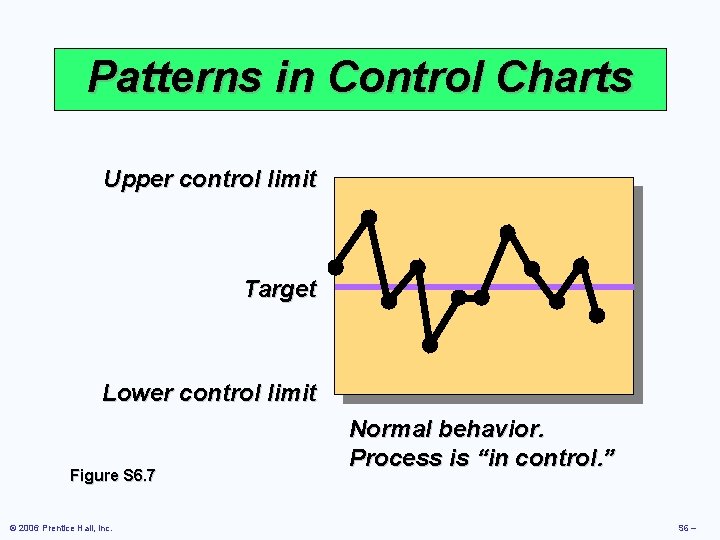
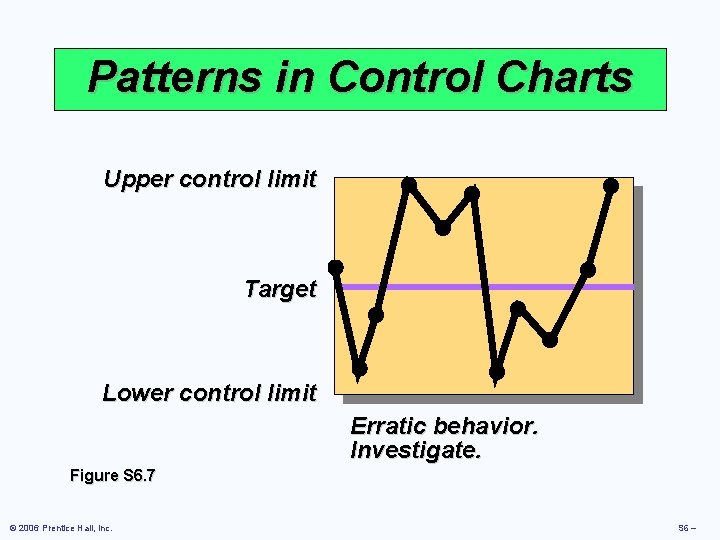
Patterns in Control Charts Upper control limit Target Lower control limit Figure S 6. 7 © 2006 Prentice Hall, Inc. Normal behavior. Process is “in control. ” S 6 –

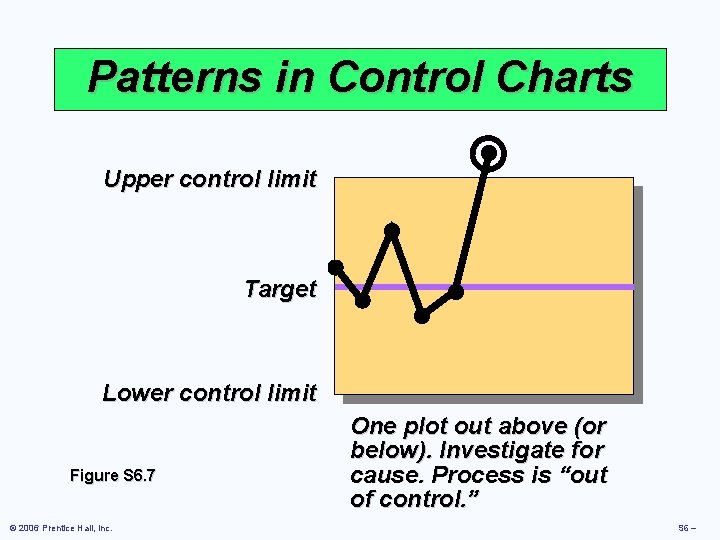
Patterns in Control Charts Upper control limit Target Lower control limit Figure S 6. 7 © 2006 Prentice Hall, Inc. One plot out above (or below). Investigate for cause. Process is “out of control. ” S 6 –

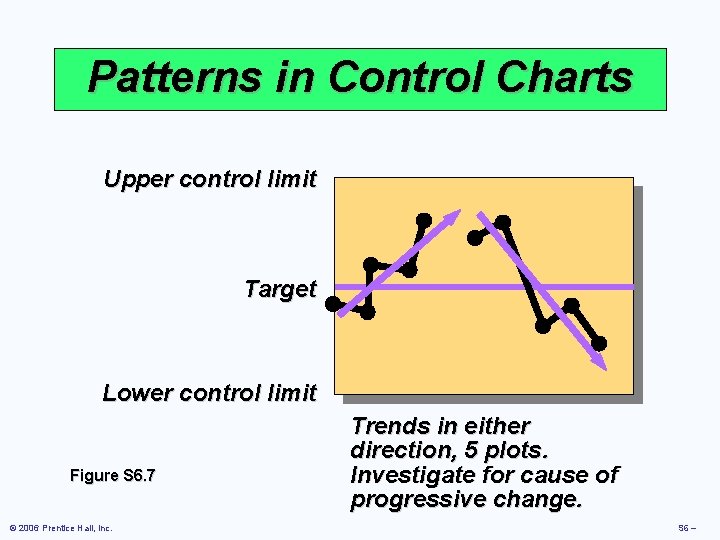
Patterns in Control Charts Upper control limit Target Lower control limit Figure S 6. 7 © 2006 Prentice Hall, Inc. Trends in either direction, 5 plots. Investigate for cause of progressive change. S 6 –

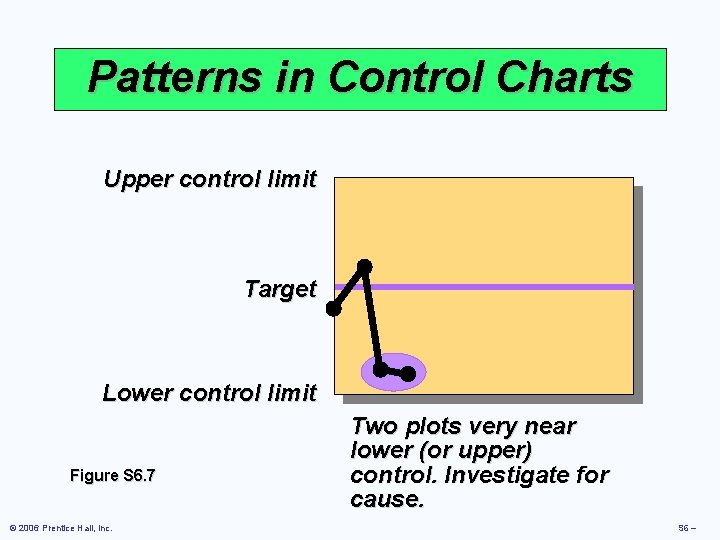
Patterns in Control Charts Upper control limit Target Lower control limit Figure S 6. 7 © 2006 Prentice Hall, Inc. Two plots very near lower (or upper) control. Investigate for cause. S 6 –

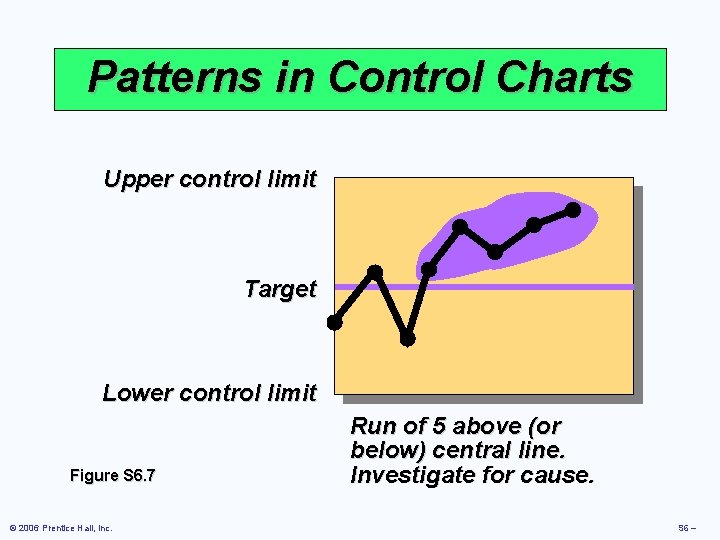
Patterns in Control Charts Upper control limit Target Lower control limit Figure S 6. 7 © 2006 Prentice Hall, Inc. Run of 5 above (or below) central line. Investigate for cause. S 6 –

Patterns in Control Charts Upper control limit Target Lower control limit Erratic behavior. Investigate. Figure S 6. 7 © 2006 Prentice Hall, Inc. S 6 –

Which Control Chart to Use Variables Data þ Using an x-chart and R-chart: þ Observations are variables þ Collect 20 - 25 samples of n = 4, or n = 5, or more, each from a stable process and compute the mean for the x-chart and range for the R-chart þ Track samples of n observations each © 2006 Prentice Hall, Inc. S 6 –

Which Control Chart to Use Attribute Data þ Using the p-chart: þ Observations are attributes that can be categorized in two states þ We deal with fraction, proportion, or percent defectives þ Have several samples, each with many observations © 2006 Prentice Hall, Inc. S 6 –

Which Control Chart to Use Attribute Data þ Using a c-Chart: þ Observations are attributes whose defects per unit of output can be counted þ The number counted is often a small part of the possible occurrences þ Defects such as number of blemishes on a desk, number of typos in a page of text, flaws in a bolt of cloth © 2006 Prentice Hall, Inc. S 6 –

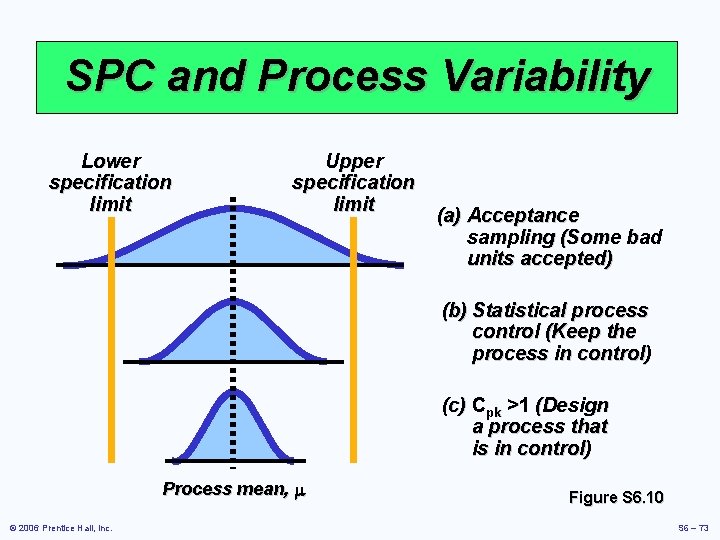
Process Capability þ The natural variation of a process should be small enough to produce products that meet the standards required þ A process in statistical control does not necessarily meet the design specifications þ Process capability is a measure of the relationship between the natural variation of the process and the design specifications © 2006 Prentice Hall, Inc. S 6 –

Process Capability Ratio Upper Specification - Lower Specification Cp = 6 s þ A capable process must have a Cp of at least 1. 0 þ Does not look at how well the process is centered in the specification range þ Often a target value of Cp = 1. 33 is used to allow for off-center processes þ Six Sigma quality requires a Cp = 2. 0 © 2006 Prentice Hall, Inc. S 6 –

Process Capability Ratio Insurance claims process Process mean x = 210. 0 minutes Process standard deviation s =. 516 minutes Design specification = 210 ± 3 minutes Upper Specification - Lower Specification Cp = 6 s © 2006 Prentice Hall, Inc. S 6 –

Process Capability Ratio Insurance claims process Process mean x = 210. 0 minutes Process standard deviation s =. 516 minutes Design specification = 210 ± 3 minutes Upper Specification - Lower Specification Cp = 6 s 213 - 207 = = 1. 938 6(. 516) © 2006 Prentice Hall, Inc. S 6 –

Process Capability Ratio Insurance claims process Process mean x = 210. 0 minutes Process standard deviation s =. 516 minutes Design specification = 210 ± 3 minutes Upper Specification - Lower Specification Cp = 6 s 213 - 207 Process is = = 1. 938 6(. 516) capable © 2006 Prentice Hall, Inc. S 6 –

Process Capability Index Upper Lower Cpk = minimum of Specification - x , x - Specification Limit 3 s 3 s þ A capable process must have a Cpk of at least 1. 0 þ A capable process is not necessarily in the center of the specification, but it falls within the specification limit at both extremes © 2006 Prentice Hall, Inc. S 6 – 59

Process Capability Index New Cutting Machine New process mean x =. 250 inches Process standard deviation s =. 0005 inches Upper Specification Limit =. 251 inches Lower Specification Limit =. 249 inches © 2006 Prentice Hall, Inc. S 6 – 60

Process Capability Index New Cutting Machine New process mean x =. 250 inches Process standard deviation s =. 0005 inches Upper Specification Limit =. 251 inches Lower Specification Limit =. 249 inches (. 251) -. 250 Cpk = minimum of , (3). 0005 © 2006 Prentice Hall, Inc. S 6 – 61

Process Capability Index New Cutting Machine New process mean x =. 250 inches Process standard deviation s =. 0005 inches Upper Specification Limit =. 251 inches Lower Specification Limit =. 249 inches (. 251) -. 250 - (. 249) Cpk = minimum of , (3). 0005 Both calculations result in. 001 Cpk = = 0. 67. 0015 © 2006 Prentice Hall, Inc. New machine is NOT capable S 6 – 62

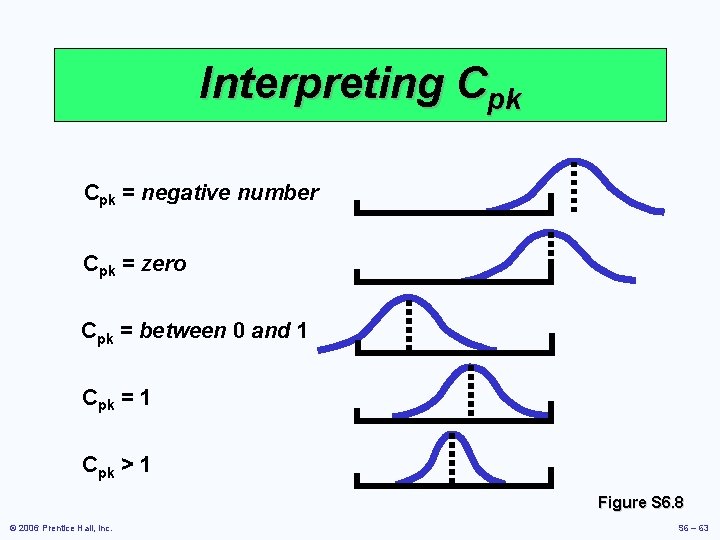
Interpreting Cpk = negative number Cpk = zero Cpk = between 0 and 1 Cpk = 1 Cpk > 1 Figure S 6. 8 © 2006 Prentice Hall, Inc. S 6 – 63

Acceptance Sampling þ Form of quality testing used for incoming materials or finished goods þ Take samples at random from a lot (shipment) of items þ Inspect each of the items in the sample þ Decide whether to reject the whole lot based on the inspection results þ Only screens lots; does not drive quality improvement efforts © 2006 Prentice Hall, Inc. S 6 –

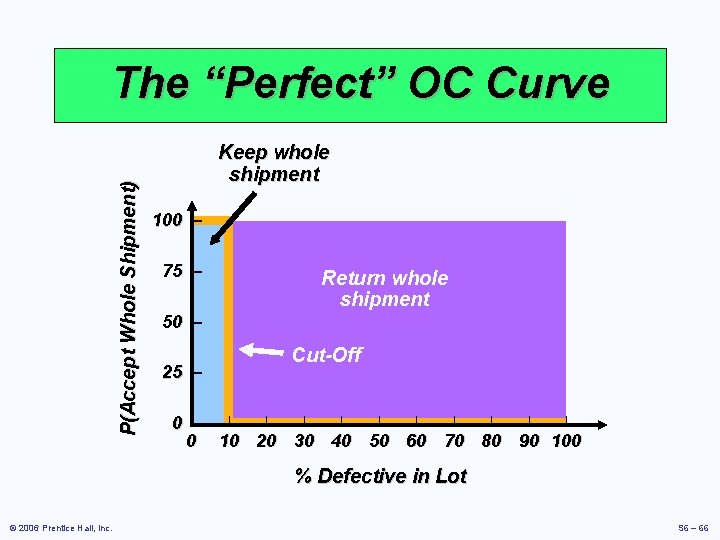
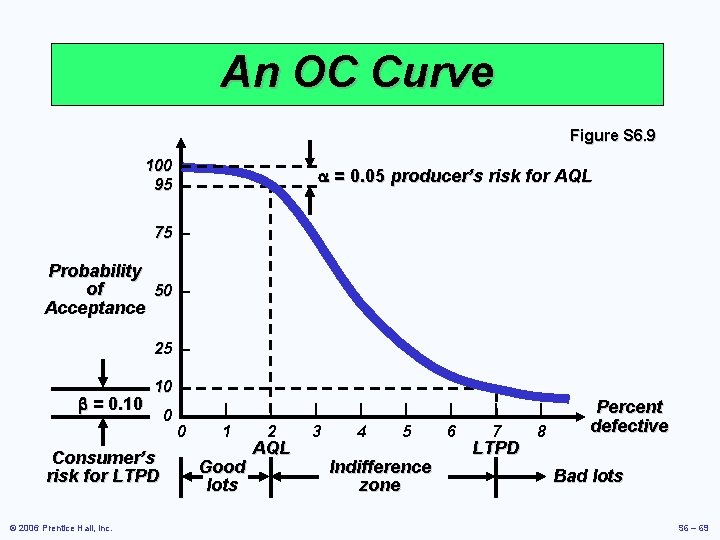
Operating Characteristic Curve þ Shows how well a sampling plan discriminates between good and bad lots (shipments) þ Shows the relationship between the probability of accepting a lot and its quality level © 2006 Prentice Hall, Inc. S 6 –

P(Accept Whole Shipment) The “Perfect” OC Curve Keep whole shipment 100 – 75 – Return whole shipment 50 – 25 – Cut-Off | | | | | 0 |– | 0 10 20 30 40 50 60 70 80 90 100 % Defective in Lot © 2006 Prentice Hall, Inc. S 6 – 66

AQL and LTPD þ Acceptable Quality Level (AQL) þ Poorest level of quality we are willing to accept þ Lot Tolerance Percent Defective (LTPD) þ Quality level we consider bad þ Consumer (buyer) does not want to accept lots with more defects than LTPD © 2006 Prentice Hall, Inc. S 6 –

Producer’s and Consumer’s Risks þ Producer's risk ( ) þ Probability of rejecting a good lot þ Probability of rejecting a lot when the fraction defective is at or above the AQL þ Consumer's risk ( ) þ Probability of accepting a bad lot þ Probability of accepting a lot when fraction defective is below the LTPD © 2006 Prentice Hall, Inc. S 6 –

An OC Curve Figure S 6. 9 100 – 95 – = 0. 05 producer’s risk for AQL 75 – Probability of 50 – Acceptance 25 – 10 – = 0. 10 0 |– 0 Consumer’s risk for LTPD © 2006 Prentice Hall, Inc. | 1 Good lots | 2 AQL | 3 | 4 | 5 Indifference zone | 6 | 7 LTPD | 8 Percent defective Bad lots S 6 – 69

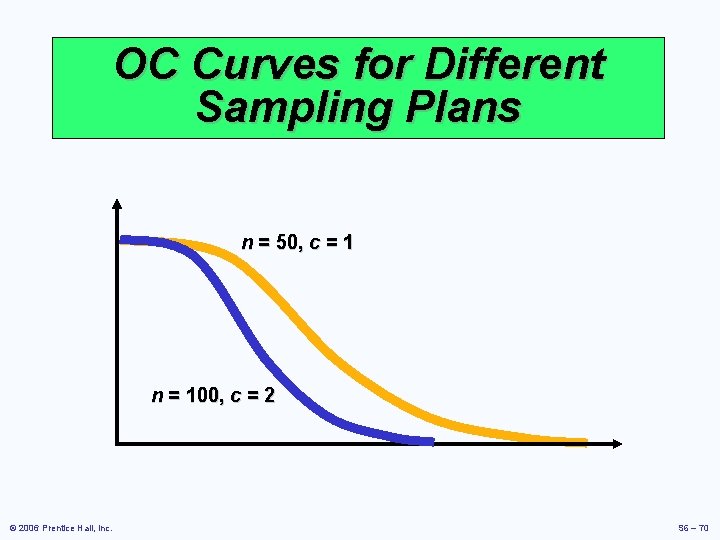
OC Curves for Different Sampling Plans n = 50, c = 1 n = 100, c = 2 © 2006 Prentice Hall, Inc. S 6 – 70

Average Outgoing Quality (Pd)(Pa)(N - n) AOQ = N where Pd = true percent defective of the lot Pa = probability of accepting the lot N = number of items in the lot n = number of items in the sample © 2006 Prentice Hall, Inc. S 6 –

Average Outgoing Quality 1. 2. If a sampling plan replaces all defectives If we know the incoming percent defective for the lot We can compute the average outgoing quality (AOQ) in percent defective The maximum AOQ is the highest percent defective or the lowest average quality and is called the average outgoing quality level (AOQL) © 2006 Prentice Hall, Inc. S 6 –

SPC and Process Variability Lower specification limit Upper specification limit (a) Acceptance sampling (Some bad units accepted) (b) Statistical process control (Keep the process in control) (c) Cpk >1 (Design a process that is in control) Process mean, m © 2006 Prentice Hall, Inc. Figure S 6. 10 S 6 – 73