On Minimizing Pattern Splitting in Multitrack String Matching

On Minimizing Pattern Splitting in Multi-track String Matching CPM 2003, Morelia, June 25 -27 Kjell Lemström and Veli Mäkinen Department of Computer Science On Minimizing Pattern Splitting in Multi-track String Matching of Helsinki University

Minimum splitting problem q We study the following problem. Given a pattern string P and K parallel text strings Tk, 1· k · K, find the smallest integer k > 0 such that P can be split into k pieces P=P 1 LPk, where each Pi has an occurrence in some text track and these partial occurrences retain the order. P T 1 T 2 T 3 CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 2

Motivation q q Music information retrieval. Text tracks represent different instruments. Finding splitted pattern occurrences allows the query-melody to jump between instruments. Useful in Query-by-Humming applications, where the pattern is monophonic and the music in database are polyphonic. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 3

CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 4

Minimum splitting problem. . . q We study different versions of the problem: - Gap between the occurrences of two consecutive pattern pieces is limited by a. - Length of each piece must be ¸ g. - Transposition-invariant occurrences; there is an occurrence if the pattern is found with a constant c added to each character. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 5

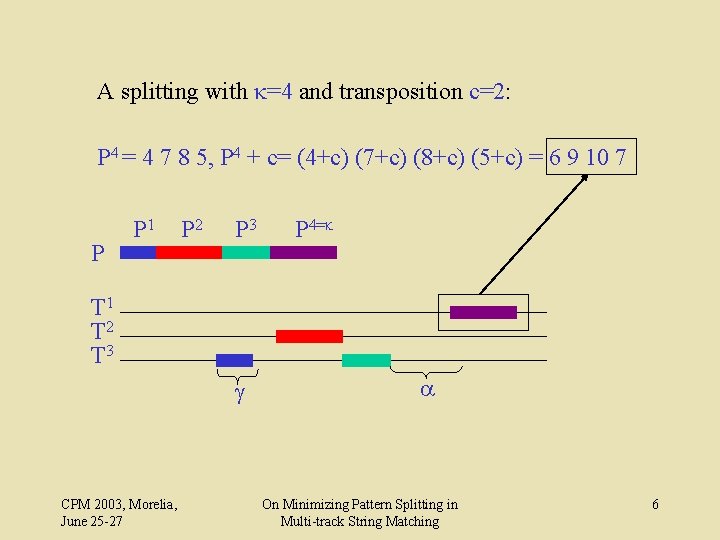
A splitting with k=4 and transposition c=2: P 4 = 4 7 8 5, P 4 + c= (4+c) (7+c) (8+c) (5+c) = 6 9 10 7 P P 1 P 2 P 3 P 4=k T 1 T 2 T 3 g CPM 2003, Morelia, June 25 -27 a On Minimizing Pattern Splitting in Multi-track String Matching 6

Parallel texts assumption q q To represent the different tracks as parallel strings, we need to add empty characters to make the tracks aligned. Therefore it makes more sense to consider splittings where the jumps over empty characters are not counted. P=464538289 CPM 2003, Morelia, June 25 -27 4 -6 --7 ---3 --9 T=. . . -5 --784 --2 -8 -. . . 3 -3 -453 -8 --8 - On Minimizing Pattern Splitting in Multi-track String Matching 7

Related work q q All related work assume that texts are parallel. The exact search (a=0), when the number of splits is not minimized, can be casted into a subset matching problem. - Running time O(Kn log 2(Kn)) can be achieved using an algorithm of Cole and Hariharan, 2002. - O((Kn+mn)d|S|/we) can be achieved using bitparallelism, see Iliopoulos and Kurokawa, 2002. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 8

Related work. . . q Lemström and Tarhio, 2003, have developed an efficient filter and a checking algorithm for the transposition-invariant version of the exact search problem on multi-track texts. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 9

Summary of results 1. 2. Let M={(i, j, k) | pi=tkj} be the set of matching character pairs, where 1· i · m, 1· j · n, and 1· k · K. For simplicity, let us assume that the alphabet is S={1, 2, . . . , Kn+m}, and m, K<n. The minimum splitting problem with a > 0, and with or without the parallel text assumption, can be solved in O(m+Kn+|M|) time. - Corollary: the transposition-invariant splitting problem can be solved in O(m. Kn) time. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 10

Summary of results. . . 1. 2. 3. Let (i, j, k)(i+1, j+1, k)L(i+l-1, j+l-1, k) be a maximal sequence of points in M, i. e. a maximal (diagonal) line segment of M. Let S be the set of all maximal line segments of M. The minimum splitting problem can be solved in O(m 2+Kn+|S|log n) time. The minimum splitting problem with a > 0 can be solved in O(m 2+Kn+|R|log n) time, where |R|· min(|S|2, |M|). CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 11

Summary of results. . . q The minimum splitting problem with a = 0 can be solved in O(m 2+k. Kn) time, where k is a given threshold. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 12

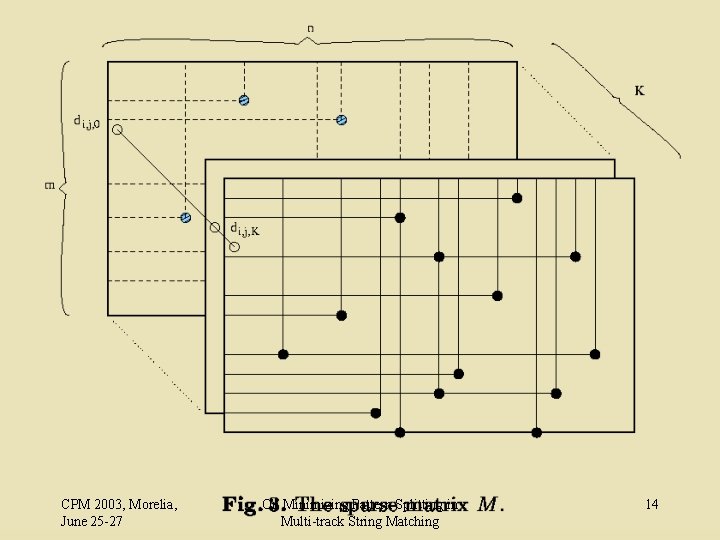
O(|M|) algorithm q The idea is to compute an m£ n £ K matrix sparsely, so that each computed cell di, j, k stores the minimum splitting needed between P 1. . . i and the text tracks upto tkj. The recurrence is CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 13

CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 14

O(|M|) algorithm. . . q q q Initializing d 1, j, k = 0 for each (1, j, k) 2 M, we have that k = 1+min{dm, j, k | (m, j, k) 2 M}. It is easy to construct M so that diagonally consecutive elements are linked to enable constant time evaluation of line (1) of the recurrence. Evaluating M column-by-column, rows bottom to up, we can maintain the minimum value at each row to enable constant time evaluation of line (2) of the recurrence. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 15

O(|M|) algorithm. . . q q To solve case a > 0, we use a technique from Crochemore et al. , 2002; keep sliding window minima at each row during column-by-column evaluation. Min-deques (Gajewska and Tarjan, 1986) support constant time access to the minimum value in a list as well as insertion to the tail and deletion from the head of the list. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 16

O(|M|) algorithm. . . q Each step of the algorithm takes constant amortized time. Thus the overall running time is O(|M|). CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 17

Transposition-invariance q q In Navarro et al. , 2003, the following connection between sparse dynamic programming and transposition-invariance was given. Lemma: Let d(P, T) be a distance between strings P and T such that its value is determined by the set M={(i, j) | pi=tj}. If an algorithm computes d(P, T) in O(|M| f(m, n)) time, then the transposition invariant distance can be computed in O(mn f(m, n)) time. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 18

Transposition-invariance. . . q q q In our problem, the relevant match sets for transposition invariant computation are the nonempty Mc={(i, j, k) | pi+c=tkj} for c 2 [-1, 1]. We can construct them all in O(m. Kn) time with pointers between diagonally consecutive elements in each set. For each set we need O(|Mc|) time computation, which is O(m. Kn) overall. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 19

Line segment algorithms 1. 2. 3. We will now show to solve the minimum splitting problem doing computation only at the endpoints of the line segments of S. After that, the construction of S is given and the solution to the case a = 0. In the sequel, we assume a single track text for simplicity. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 20

Interpretation as a minimum jump distance CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 21

Interpretation as a minimum jump distance q q q We denote the two endpoints of a line segment S by start(S), end(S) 2 M. Let minimum jump distance d((i, j)) to (i, j) 2 S be the number of horizontal jumps (from (i’-1, j’’) 2 S’’ to (i’, j’) 2 S’, j’<j, S’’, S’ 2 S) needed for traversing through line segments of S from row 1 to (i, j). Then di, j = 1+d((i, j)), where di, j denotes the minimum splitting upto (i, j). CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 22

Interpretation as a minimum jump distance. . . q q Lemma: The minimum jump distance d(end(S)) equals d(start(S)). Let us denote this value d(S). Idea of the algorithm: Traverse the endpoints of the line segments row-by-row. Keep the active segments (those intersecting previous row) in a balanced binary search tree with the diagonal numbers as the keys. Maintain subtree minima of d(S) values to answer range minimum queries [-1, j -i). CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 23

Interpretation as a minimum jump distance. . . q q The required operations on binary search tree can be supported in O(log n) time. Thus, the algorithm works in O(|S|log n) time. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 24

Minimum splitting with a>0 q q One can prove that it is enough to recompute the values of line segments only in their intersections with the so called a-greedy paths. With some care in the implementation, one gets time bound O(m 2+Kn+|R|log n), where |R|· min(|S|2, |M|). CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 25

Minimum splitting with a>0. . . CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 26

Constructing S q q q We will give a more general algorithm that constructs set Sg, i. e. , the set of maximal line segments of length at least g. Let Prefix(A, B) denote the length of the longest common prefix of strings A and B. Let Max. Prefix(j) be max{Prefix(Pi. . . m, Tj. . . n) | 1· i · m} and H(j) some index i giving the maximum. A=aaabbbb Prefix(A, B)=aaab B=aaabcbb CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 27

Constructing S. . . q q Let Jump(i, j) denote Prefix(Pi. . . m, Tj. . . n). Lemma (Ukkonen and Wood, 1993): Jump(i, j)=min(Max. Prefix(j), Prefix(Pi. . . m, PH(j). . . m). Ukkonen and Wood show to allow constant access to any Jump(i, j) value after O(m 2+n) time preprocessing. Observation: If we manage to call Jump(i, j) only at points (i, j)=start(S), S 2 Sg, we have an O(|Sg|) construction algorithm for Sg. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 28

Constructing S. . . q q q To find points (i, j)=start(S), S 2 Sg, we construct the suffix array A of P. We make a copy As of A for each distinct character s of P. Then we remove from each As the suffixes i such that pi-1=s. Now, if we query Tj. . . j+g-1 from the suffix array As where s = tj-1 (or from A if As does not exist), the resulting positions of P give the line segments that start at column j. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 29

Constructing S. . . q q q If we associate all suffix arrays with LCP values, the overall complexity of constructing Sg is O(m 2+Kn(g+log m)+|Sg|). Using suffix trees instead gives a bound O(m 2| P|+Kng+|Sg|) A more direct approach gives O(m 2+Kn+|S|) for the case g = 1. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 30

Minimum splitting with a=0 q Fact: Let there be a splitting of the pattern into k pieces, starting at position j of the multi-track text, without gaps between the partial occurrences. Then there is an equally good occurrence that can be found as follows: Select track Tk whose jth suffix has the longest common prefix, say length l, with the pattern. Iterate the same algorithm from position j+l with pattern suffix Pl+1. . . m, until a splitting into k pieces is found. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 31

Minimum splitting with a=0. . . q q In the above algorithm, we need k queries to Jump(i, j) for each track at each position j. Thus, after O(m 2+Kn) preprocessing for Jump(i, j) queries, the problem can be solved in O(k. Kn) time. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 32

Implementation q q q We implemented the O(|M|) time algorithm, with the aforementioned skipping of empty characters. Instead of using min-deques to support sliding window minima computation, we used a modification of the linear time construction of Cartesian trees (simple to implement and fast in practice). The algorithm is plugged into the C-BRAHMS music search engine. CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 33

http: //www. cs. helsinki. fi/group/ cbrahms/demoengine/ CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 34

Extension and open problems q q q The O(|M|) and O(|S|log n) algorithms can be extended to the case where the cost is the sum of the lengths of the gaps between the partial occurrences. Open: Computation in the case of the g restriction on the lengths of the partial occurrences. Open: Can one achieve O(m+Kn+|Sg|) time for constructing Sg? CPM 2003, Morelia, June 25 -27 On Minimizing Pattern Splitting in Multi-track String Matching 35