On Evaluation of Graph Pattern Matching in Large

On Evaluation of Graph Pattern Matching in Large Graph Databases Yangjun Chen Bin Guo Xingyue Huang Dept. Applied Computer Science, University of Winnipeg 515 Portage Ave. Winnipeg, Manitoba, Canada R 3 B 2 E 9

Outline n n Motivation Algorithm for Graph Pattern matching - n n -transitive closures Relation Signatures and Vertex Counters main algorithm: triangle consistency Experiments Conclusion

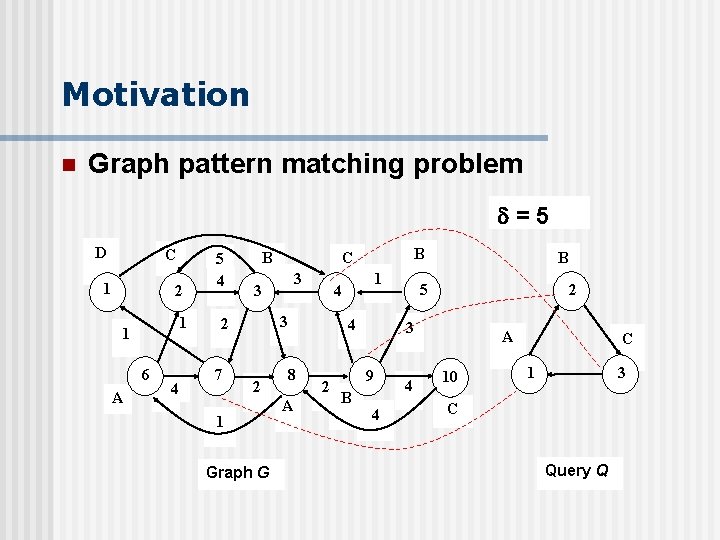
Motivation n Graph pattern matching problem Given a data graph G, a query graph Q with n vertices {v 1, . . . , vn} and a parameter δ, the evaluation of Q reports all matching results <u 1, … un> in G if the following conditions hold: 1) label(ui) = label(vi) for 1 ≤ i ≤ n; 2) For any edge (vi, vj) Q, the distance between ui and uj in G is no larger than δ, i. e. , Dist(ui, uj) ≤ δ.

Motivation n Graph pattern matching problem =5 D C 1 2 1 1 6 A A 4 5 4 B 7 3 3 2 1 Graph G 8 A 1 4 3 2 B C 4 2 2 5 3 9 B B 4 4 A 10 C 1 3 C Query Q

Motivation n Application Schema matching to part of a database instance Matching in large metabolic network Computer vision, by which a scene is represented as a graph

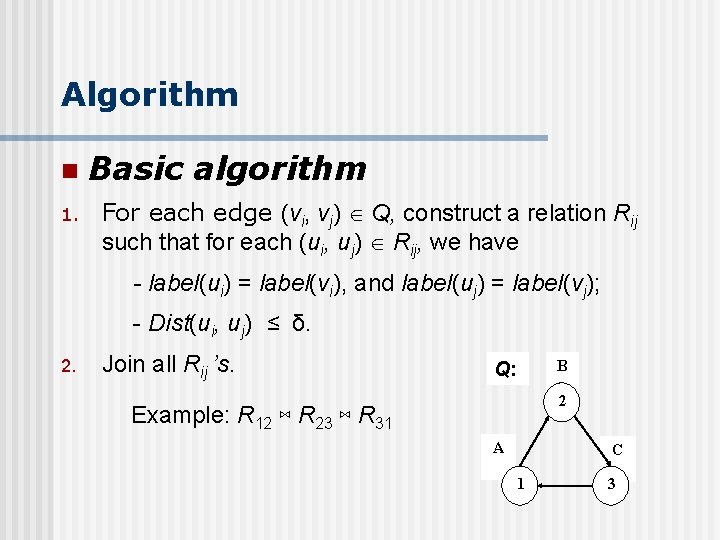
Algorithm n 1. Basic algorithm For each edge (vi, vj) Q, construct a relation Rij such that for each (ui, uj) Rij, we have - label(ui) = label(vi), and label(uj) = label(vj); - Dist(ui, uj) ≤ δ. 2. Join all Rij ’s. B Q: 2 Example: R 12 ⋈ R 23 ⋈ R 31 A C 1 3

Algorithm n Improved algorithm 1. For graph G, construct a δ-transitive closure for it as part of an index. 2. To speed up join operations, do the following: - construct relation signatures and vertex counters as part of the index. - check triangle consistency to filter useless tuples. - join all the reduced relations.

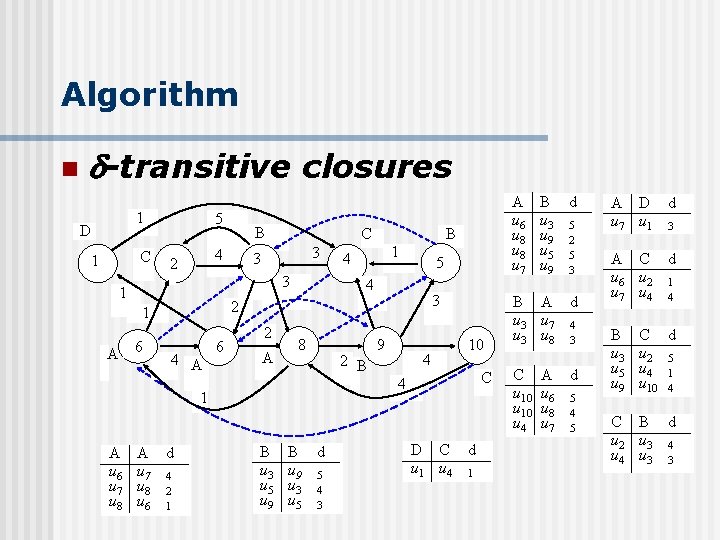
Algorithm n -transitive closures Definition ( -transitive closures) Let G = (V, E, Σ) be a directed, weighted graph, where V – set of vertices E – set of edges Σ – set of labels (for vertices). Let > 0 be a positive number. A -transitive closure of G, denoted G , is a graph such that V(G ) = V, and there is an edge (u, u ) E(G ) if and only if dist(u, u ) .

Algorithm n -transitive closures 1 D C 1 5 4 2 3 3 B 5 4 4 A 6 2 A 8 1 A u 6 u 7 u 8 1 4 3 2 1 6 B C 3 1 A B A d u 7 4 u 8 2 u 6 1 B u 3 u 5 u 9 B d u 9 5 u 3 4 u 5 3 2 B A u 6 u 8 u 7 9 4 10 4 D C d u 1 u 4 1 C B d u 3 5 u 9 2 u 5 5 u 9 3 B A d u 3 u 7 4 u 3 u 8 3 C u 10 u 4 A d u 6 5 u 8 4 u 7 5 A D d u 7 u 1 3 A C d u 6 u 2 1 u 7 u 4 4 B u 3 u 5 u 9 C d u 2 5 u 4 1 u 10 4 C B d u 2 u 3 4 u 3 3

Algorithm n Relation Signatures - Consider G(V, E, ). Let = {l 1, …, lk}. We will divide all the vertices into | | disjoint lists, denoted as D[l 1], …, D[lk] such that D[l 1] …, D[lk] = V, D[li] D[lj] = for i j, and all the vertices in a D[li] have the same label li. Then, we sort all vertices in D[li] in ascending order by their vertex IDs and refer to each vertex by its order number. - For example, for the graph shown in Fig. 1(a), we have D[A] = {u 6, u 7, u 8}. Thus, u 6 is the first vertex, u 7 the second, and u 8 the third in D[A].

Algorithm n Relation Signatures - In this way, a vertex in G can be referred to as a pair (l, i), where l is a label, and i is the order number of the vertex in D[l]. For example, u 6 can be represented as (A, 1). Let R be a relation in G corresponding to a pair of vertex labels (l, l ). Denote by R[1] and R[2] all vertices in the first and the second column, respectively. Then, all the vertices in R[1] (R[2]) can be represented by a bit string s of length |D[l]| (resp. |D[l ]|) such that s[i] = 1 if the ith vertex of D[l] (resp. D[l ]|) appears in R[1] (resp. R[2]). Otherwise, s[i] = 0. Let s, s be the bit string for R[1] and (R[2]), respectively. We call S = [s | s ] the signature of R, respectively referred to as R. S[1] = s and R. S[2] = s. - -

Algorithm n Relation Signatures R 1 : A u 6 u 8 u 7 B u 3 u 9 u 5 u 9 d 5 2 5 3 R 2 : R 5 : B u 3 u 5 u 9 C u 2 u 4 u 10 d 5 1 4 C R 6: u 10 u 4 A u 6 u 8 u 7 d 5 4 5 R 7 : R 8 : A u 6 u 7 u 8 A u 7 u 8 u 6 d 4 2 1 B u 3 u 5 u 9 B u 9 u 3 u 5 d 5 4 3 R 10: domains: A 1 u 6 2 u 7 3 u 8 R 9 : A D d u 7 u 1 3 B 1 u 3 2 u 5 3 u 10 A C d R 3: u 6 u 2 1 u 7 u 4 4 C 1 u 2 2 u 4 3 u 10 C B d u 2 u 3 4 u 3 3 D C d u 1 u 4 1 D 1 u 1 R 4: Bu 3 R 1 : R 2 : R 3 : R 4 : R 5 : R 6 : R 7 : R 8 : R 9 : R 10: A d u 7 4 u 8 3 [111 | 111] [010 | 1] [110 | 110] [100 | 011] [111 | 111] [011 | 111] [110 | 100] [111 | 111] [1 | 010]

Algorithm n Vertex Counters - By using relation signatures, we are able to indicate whether a vertex appears in a column of a certain relation. However, the information on how many times it appears in that column is missing. So, for each vertex u in a domain D[l] for a label l, we will also associate it with a set of counters each for a column in a different relation, in which it occurs. -

Algorithm n Vertex Counters - Assume that u is a vertex appearing in the first column of some Ri. Then, it will have a counter, denoted as u. Ci[1], to record how many times it appears in that column of Ri. In general, if it appears in k columns (respectively from different relations), it will be associated with k counters. -

Algorithm n Vertex Counters - For example, u 6 (represented by (A, 1)) appears in 6 columns: R 1[1], R 3[1], R 4[2], R 6[2], R 8[1] and R 8[2]. Thus, u 6 will be associated with 6 counters: u 6. C 1[1] = 1, u 6. C 3[1] = 1, u 6. C 4[2] = 1, u 6. C 6[2] = 1, u 6. C 8[1] = 1, u 6. C 8[2] = 1. - u 8 (represented by (A, 3)) appears only in 5 columns. Thus, it has 5 counters: u 8. C 1[1] = 2, u 8. C 4[2] = 1, u 8. C 6[2] = 1, u 8. C 8[1] = 1, u 8. C 8[2] = 1.

Algorithm n Filtering - When a query Q with parameter arrives, a simple way to evaluate it can be described as follows. First, we locate all the relevant relations (in G ). Then, for each edge (vi, vj) Q, remove all those tuples <u, u > with dist(u, u ) > from the corresponding relation Rij = R(label(vi), label(vj)). Next, we join such Rij’s to form the final result.

Algorithm However, we can do better by filtering all those tuples which cannot contribute to the final result before the joins are carried out. To this end, we need a new concept of triangle consistency. Triangle Consistency Definition (triangle consistency) Let Q be a query with parameter . Let (vi, vj) be an edge in Q. A tuple t = <u, u > Rij in G with is said to be triangle consistent with respect to a vertex vk (k i, j) in Q if for Rjk, or Rkj, and Rik, or Rki in G , one of the following conditions is satisfied:

Algorithm - if vk is incident to vj but not to vi, then there exists u such that <u , u > Rjk if (vj, vk) Q, or <u , u > Rkj if (vk, vj) Q; - if vk is incident to vi but not to vj, then there exists u such that <u , u > Rik if (vi, vk) Q, or <u , u > Rki if (vk, vi) Q; if vk is incident to both vi and vj, then there exists u such that <u, u > Rik and <u , u > Rkj if (vi, vk), (vk, vj) Q; or <u, u > Rik and <u , u > Rjk if (vi, vk), (vj, vk) Q; or <u , u> Rki and <u , u > Rjk if (vk, vi), (vk, vj) Q; or <u , u> Rki and <u , u > Rkj if (vk, vi), (vj, vk) Q. -

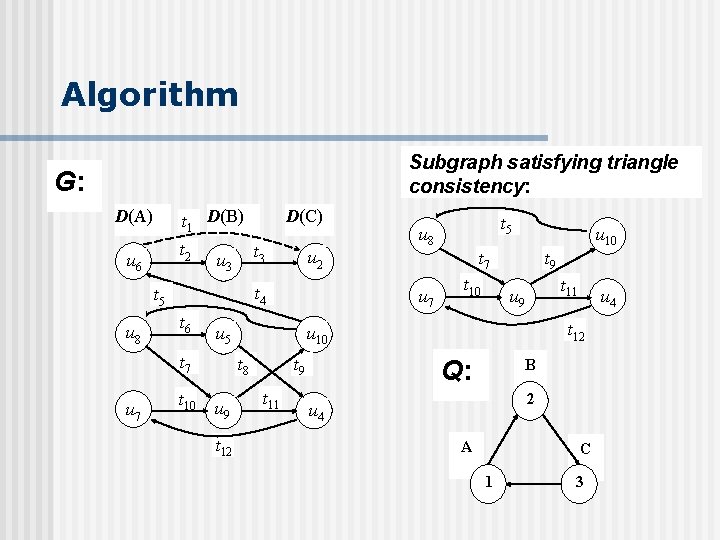
Algorithm Subgraph satisfying triangle consistency: G: D(A) t 1 D(B) t 2 u 6 t 3 u 3 t 6 t 10 t 12 u 10 t 7 t 10 t 9 t 11 u 4 t 12 u 10 t 8 u 9 t 5 u 8 u 7 u 5 t 7 u 2 t 4 t 5 u 8 D(C) Q: B 2 u 4 A C 1 3

Algorithm n Do the relation filtering based on the triangle consistency n Do the joins on the reduced Rij’s

n Experiments In our experiments, we have tested altogether three different methods: n n n 2 -hop-based [1] (2 Hb for short), LLR-embedding-based [2] (LLRb for short), Our method discussed in this paper. [1] J. Cheng, J. X. Yu, B. Ding, P. S. Yu, and H. Wang, “Fast graph pattern matching, ” Proc. Int. Conf. ICDE. , pp. 913– 922, 2008. [2] L. Zou, L. Chen, and M. Özsu, “Distance-Join  Pattern Match Query In a Large Graph, ” VLDB, vol. 2, no. 1, pp. 886– 897, 2009.

n Experiments - All the three methods have been implemented in C++, compiled by GNU make utility with optimization of level 2. - All of our experiments are performed on a 64 -bit Ubuntu operating system, run on a single core of a 2. 40 GHz Intel Xeon E 52630 processor with 32 GB RAM.

n Experiments Tested data (graphs): data graph |V| yeast 2, 361 wiki. Vote 7, 115 cite. Hepph 34, 546 web. Stanford 281, 903 com. DBLP 317, 080 web. Notre. Dame 325, 729 citeseer 384, 413 web. Berk. Stan 685, 230 web. Google 875, 713 road. Net. PA 1, 088, 092 road. Net. TX 1, 379, 917 cite. Patterns 3, 774, 768 |E| 7, 182 103, 689 421, 578 2, 312, 497 1, 049, 866 1, 497, 134 1, 751, 463 7, 600, 595 5, 105, 039 1, 541, 898 1, 921, 660 16, 518, 948 | | 12 100 124 100 13, 477 100 500 500 500 1, 1319 directed weight syn. label no yes yes no no yes 1 1 1 -10 1 -10 no yes yes yes no

n Experiments Patterns:

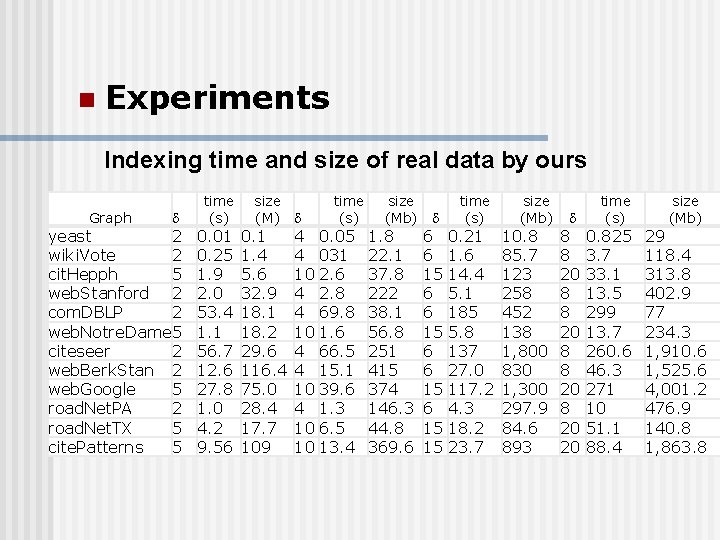
n Experiments Indexing time and size of real data by ours Graph yeast 2 wiki. Vote 2 cit. Hepph 5 web. Stanford 2 com. DBLP 2 web. Notre. Dame 5 citeseer 2 web. Berk. Stan 2 web. Google 5 road. Net. PA 2 road. Net. TX 5 cite. Patterns 5 time (s) 0. 01 0. 25 1. 9 2. 0 53. 4 1. 1 56. 7 12. 6 27. 8 1. 0 4. 2 9. 56 size (M) 0. 1 1. 4 5. 6 32. 9 18. 1 18. 2 29. 6 116. 4 75. 0 28. 4 17. 7 109 time (s) 4 0. 05 4 031 10 2. 6 4 2. 8 4 69. 8 10 1. 6 4 66. 5 4 15. 1 10 39. 6 4 1. 3 10 6. 5 10 13. 4 size (Mb) 1. 8 22. 1 37. 8 222 38. 1 56. 8 251 415 374 146. 3 44. 8 369. 6 time (s) 6 0. 21 6 15 14. 4 6 5. 1 6 185 15 5. 8 6 137 6 27. 0 15 117. 2 6 4. 3 15 18. 2 15 23. 7 size (Mb) 10. 8 85. 7 123 258 452 138 1, 800 830 1, 300 297. 9 84. 6 893 8 8 20 20 time (s) 0. 825 3. 7 33. 1 13. 5 299 13. 7 260. 6 46. 3 271 10 51. 1 88. 4 size (Mb) 29 118. 4 313. 8 402. 9 77 234. 3 1, 910. 6 1, 525. 6 4, 001. 2 476. 9 140. 8 1, 863. 8

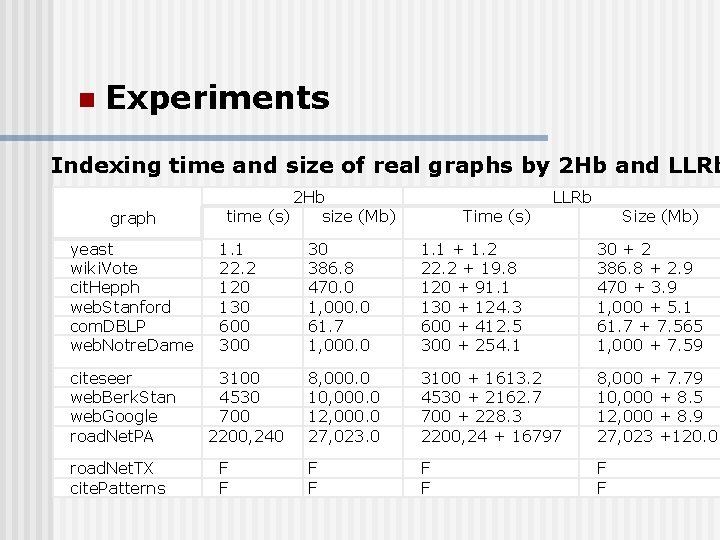
n Experiments Indexing time and size of real graphs by 2 Hb and LLRb graph yeast wiki. Vote cit. Hepph web. Stanford com. DBLP web. Notre. Dame citeseer web. Berk. Stan web. Google road. Net. PA road. Net. TX cite. Patterns 2 Hb time (s) size (Mb) 1. 1 22. 2 120 130 600 3100 4530 700 2200, 240 F F Time (s) LLRb Size (Mb) 30 386. 8 470. 0 1, 000. 0 61. 7 1, 000. 0 1. 1 + 1. 2 22. 2 + 19. 8 120 + 91. 1 130 + 124. 3 600 + 412. 5 300 + 254. 1 30 + 2 386. 8 + 2. 9 470 + 3. 9 1, 000 + 5. 1 61. 7 + 7. 565 1, 000 + 7. 59 8, 000. 0 10, 000. 0 12, 000. 0 27, 023. 0 3100 + 1613. 2 4530 + 2162. 7 700 + 228. 3 2200, 24 + 16797 8, 000 + 7. 79 10, 000 + 8. 5 12, 000 + 8. 9 27, 023 +120. 0 F F F

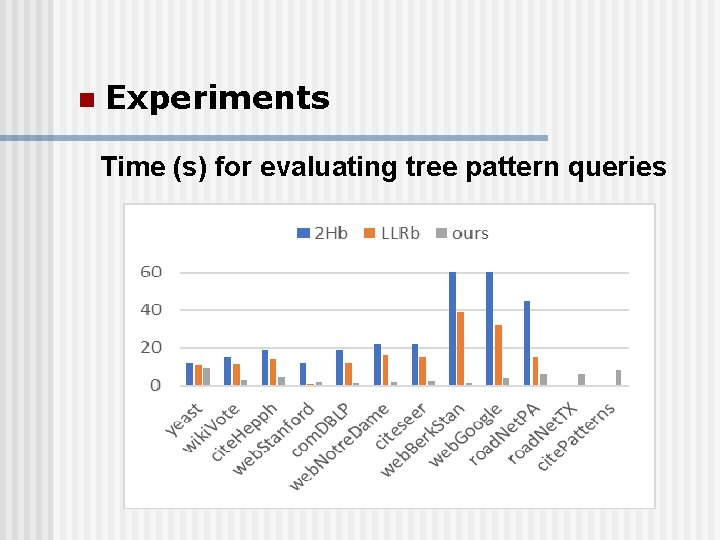
n Experiments Time (s) for evaluating tree pattern queries

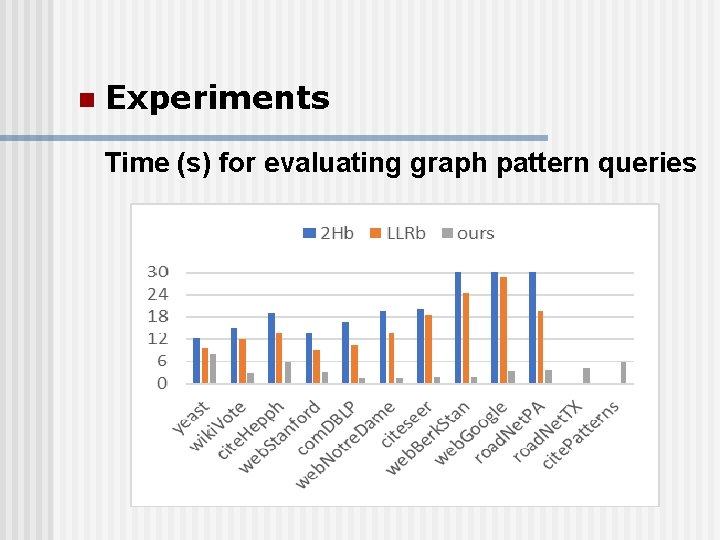
n Experiments Time (s) for evaluating graph pattern queries

n Conclusion and Future Work Ø Algorithm for evaluating graph pattern queries based on the following techniques: - -transitive closures - Relation Signatures and Vertex Counters - main algorithm: triangle consistency Ø Future work - When is large, a -transitive closure can be very big. - How to efficiently create a -transitive closure?