Nonlinear MHD simulations of ELMs Emiel van der

Nonlinear MHD simulations of ELMs Emiel van der Plas Guido Huijsmans Association Euratom-CEA Cadarache Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

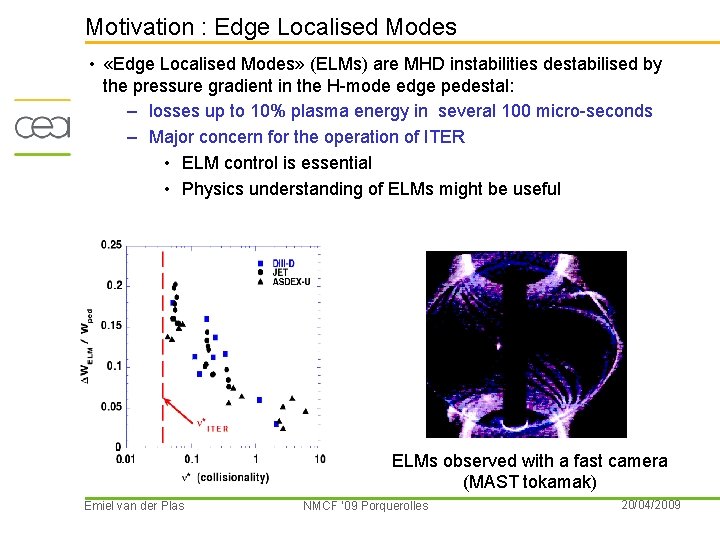
Motivation : Edge Localised Modes • «Edge Localised Modes» (ELMs) are MHD instabilities destabilised by the pressure gradient in the H-mode edge pedestal: – losses up to 10% plasma energy in several 100 micro-seconds – Major concern for the operation of ITER • ELM control is essential • Physics understanding of ELMs might be useful ELMs observed with a fast camera (MAST tokamak) Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

ELMs • The physics of the ELMs is still not well understood: – How to extrapolate to ITER parameters • MHD stability limits are well known: – Ballooning modes (and peeling modes) – Good agreement with experiment • Many open questions on the non-linear evolution: – What determines the size of an ELM? – How can a plasma become strongly unstable? – What is the relaxation mechanism? ELM physics studies by numerical simulation – Proposal ANR-CIS 2006: project ASTER ‘The objective of this project is the high resolution MHD simulation of a complete cycle of the ELM instability, from its onset, the highly non-linear phase and its decay. ’ Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

ANR-CIS projet ASTER: Adaptive mhd Simulation of Tokamak Elms for ite. R Rémi Abgrall Marina Bécoulet Olivier Coulaud Pascal Hénon Robin Huart Guido Huysmans Boniface N’Konga Stanislas Pamela Emiel van der Plas Pierre Ramet Alessandro Liberati Emiel van der Plas (Prof, MAB, Univ. Bdx 1) (CR, CEA/IRFM) (DR INRIA) (CR INRIA) (thesard, Md. C, MAB, Univ Bdx 1) (CR, CEA/IRFM) (Prof, Univ. Nice/ Md. C, Univ Bdx 1) (thesard, CEA/IRFM) (postdoc, CEA/IRFM) (Md. C, Labri, Univ Bdx 1) (postdoc, Labri, Univ. Bdx 1) NMCF ’ 09 Porquerolles 20/04/2009

Project ANR-CIS 2006. 001 : ASTER • Development of high-resolution non-linear MHD code(s) for the simulation of ELMs in ITER – Using the expertise of the fluid dynamics community to develop non-linear MHD simulation codes • Extension of the CFD code Fluidbox to MHD – Continued development of the code JOREK • Physics model, numerical methods – FLUIDBOX and JOREK use the same fully implicit methods leading to large sparse systems of equations: • Continued development of the Pasti. X sparse matrix library – adaptive grid refinement • application to the study of the physics of ELMs • Collaboration IRFM Cadarache & Labri, MAB et INRIA Bordeaux • ASTER finances: postdoc Emiel van der Plas, Ph. D Stanislas Pamela 1 postdoc (Labri) et 1 Ph. D (MAB) site web : http: //aster. gforge. inria. fr Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK 2 nonlinear MHD code • JOREK has been developed with the specific aim to simulate ELMs – non-linear MHD – domain with closed and open field lines • New version: (JOREK 2): – Discretisation: • Cubic finite elements in the poloidal plane • Fourier series in toroidal angle – Time stepping: • fully implicit Crank-Nicholson (no splitting) – Solver sparse matrices: • GMRES with ‘physics’ based preconditioner • Preconditioner per toroidal harmonic using Pasti. X • N(dof) ~ 5 x 106 – Parallelisation using MPI (+threads, Pasti. X) • Distribution of elements, matrix construction • Matrix solution GMRES, Pasti. X Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

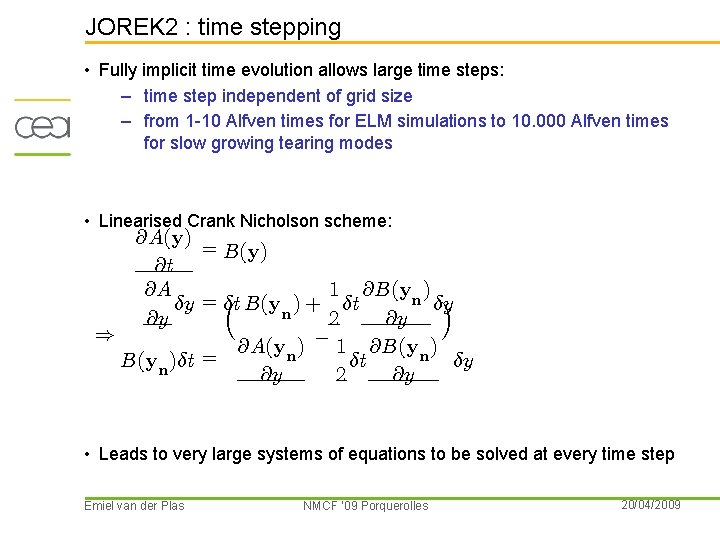
JOREK 2 : time stepping • Fully implicit time evolution allows large time steps: – time step independent of grid size – from 1 -10 Alfven times for ELM simulations to 10. 000 Alfven times for slow growing tearing modes • Linearised Crank Nicholson scheme: @A(y) = B(y) @t @A 1 @B(yn ) ´ ±y = ³ ±t B(yn ) + ±t ±y @y 2 @y ) @A(yn ) ¡ 1 @B(yn ) ±t ±y B(yn )±t = @y 2 @y • Leads to very large systems of equations to be solved at every time step Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK Boundary Conditions • Wall parallel to field lines: – all variables constant in time • Wall crossing field lines: – Free outflow of density and temperature – Mach 1 parallel flow vk = c = s ¢ p ¢ ° Tdivertor ¢ k • Generalised to includekpoloidal flow component: v n + v. E n = vj knj v Emiel van der Plas NMCF ’ 09 Porquerolles cs 20/04/2009

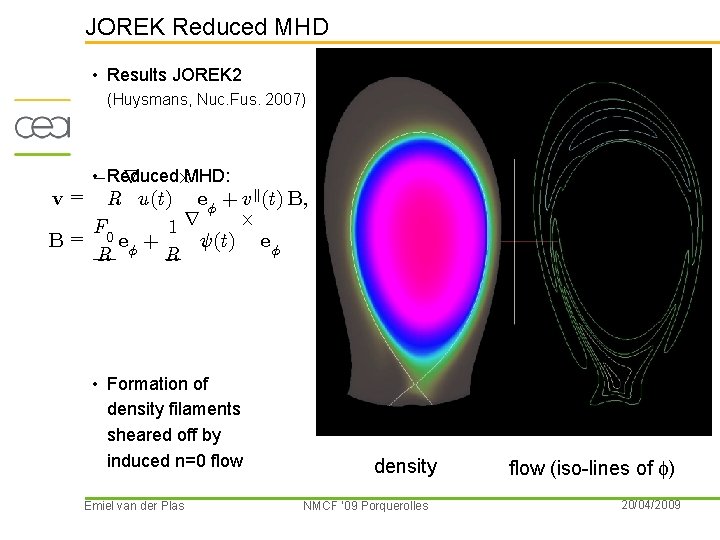
JOREK Reduced MHD • Results JOREK 2 (Huysmans, Nuc. Fus. 2007) • Reduced ¡ £MHD: r v = R u(t) eÁ + vk(t) B; £ 1 r F 0 Ã(t) eÁ B= eÁ + R R • Formation of density filaments sheared off by induced n=0 flow Emiel van der Plas density NMCF ’ 09 Porquerolles flow (iso-lines of f) 20/04/2009

JOREK development : full MHD comparison with experiment (growth rates etc) ! • Introduces new physics compressibility, (fast) magneto-acoustic waves effects of parallel flow parallel vs perpendicular physics untangled ¡r ¢ r¢ r full = MHD equations: ½ (½v) + (D ½) + S½ ; @The t ¡ ¢r ¡r £ r 2 v; ½@t v = ¡½v¢ r v¡ ¡ + ¢º r (½T ) +r. J¢ B r (· T ) + ST ; @t T = v £ r. T£ (°¡ 1)T r £ rv£+ A) ´( A): @A=v ( t – Vector equations Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

Vector basis J r £r • Use the local Á); a 1 = ( t coordinates: J r £r a 2 = ( Á s); J r £r a 3 = ( s t); g 12 r a 1 = s; r a 2 = t; r a 3 = Á; J jr j • Then metric 2 tensor g 11 = Á 2 t 2; J jr j 2 Á 2 s 2; g 22 = ¡J jr j r ¢ r 2 =g = Á2 s t; 21 jr j¡ J jr j g = 2 s 2 t 2 = Á 2 = R 2 33 g 11 g 22 g 12 = g 21 g 33 jr j = s 2; jr j = t 2; r ¢r = s t; 1 = : 2 R ´ 1 ¶ ¡ ¶ µ ¡k gmk (@i gmj + @j gim @m gij ): 2 • Christoffel symbols ij ¡ 1 ys sx t x ¡yt = sy ty xt xs J 2 D • But how to obtain µ Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

Example: Jx. B force • Choose v covariant, A contravariant, so • Then • and • so Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

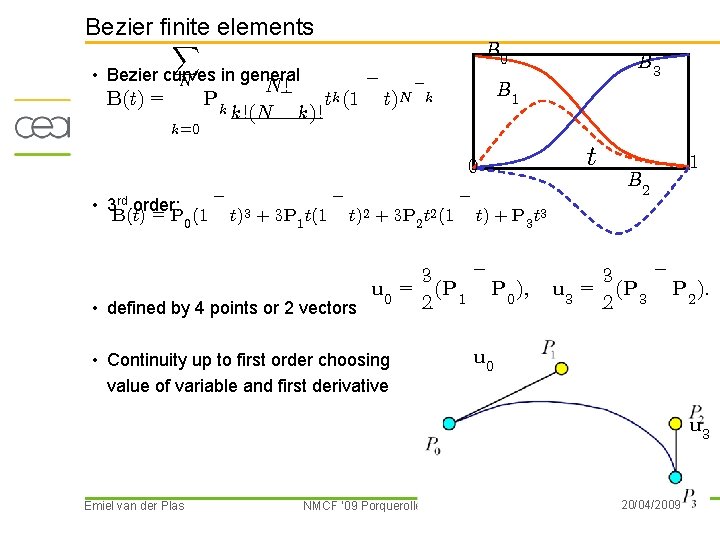
Bezier finite elements X B 0 • Bezier curves in general N B(t) = k=0 ¡ ¡ ! N¡ Pk tk (1 t)N k k!(N k)! B 1 0 • 3 rd order: B(t) = P 0 (1 ¡ t)3 + 3 P 1 t(1 ¡ t)2 + 3 P 2 t 2 (1 ¡ t B 2 1 t) + P 3 t 3 ¡ 3 u 0 = (P 1 P 0 ); 2 • defined by 4 points or 2 vectors • Continuity up to first order choosing value of variable and first derivative B 3 ¡ 3 u 3 = (P 3 P 2 ): 2 u 0 u 3 Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

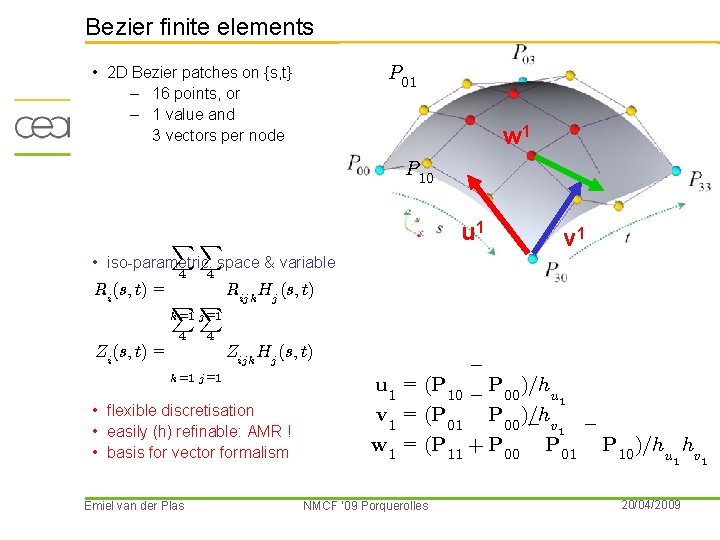
Bezier finite elements • 2 D Bezier patches on {s, t} – 16 points, or – 1 value and 3 vectors per node P 01 w 1 P 10 XX u 1 v 1 • iso-parametric: space & variable 4 Ri (s; t) = 4 XX Rijk Hj (s; t) k=1 j =1 4 Zi (s; t) = 4 Zijk Hj (s; t) k=1 j =1 • flexible discretisation • easily (h) refinable: AMR ! • basis for vector formalism Emiel van der Plas ¡ u 1 = (P 10 ¡ P 00 )=hu 1 = v 1 (P 01 P 00 )=h ¡ v 1 ¡ w 1 = (P 11 + P 00 P 01 P 10 )=hu hv 1 NMCF ’ 09 Porquerolles 20/04/2009 1

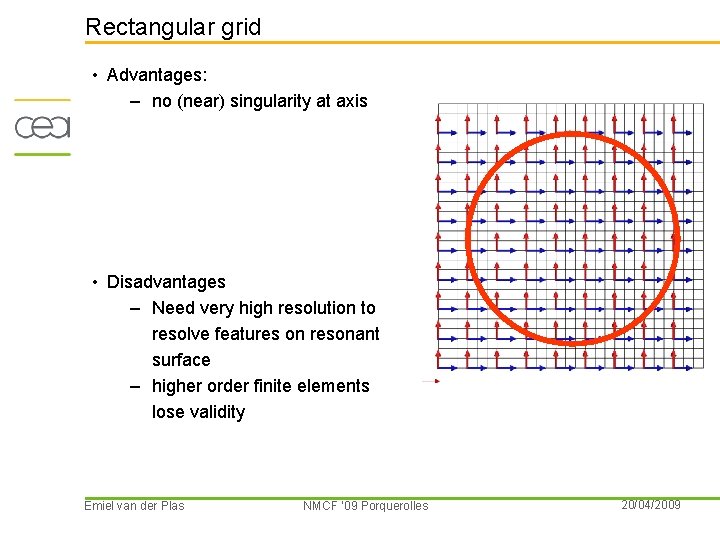
Rectangular grid • Advantages: – no (near) singularity at axis • Disadvantages – Need very high resolution to resolve features on resonant surface – higher order finite elements lose validity Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

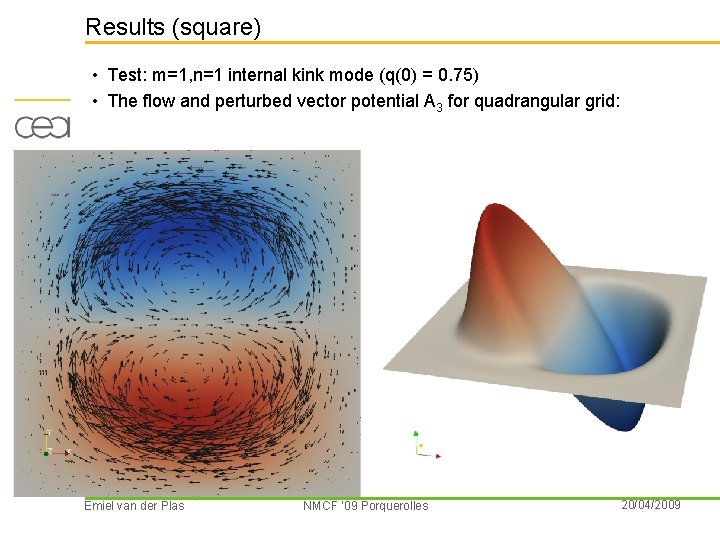
Results (square) • Test: m=1, n=1 internal kink mode (q(0) = 0. 75) • The flow and perturbed vector potential A 3 for quadrangular grid: Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

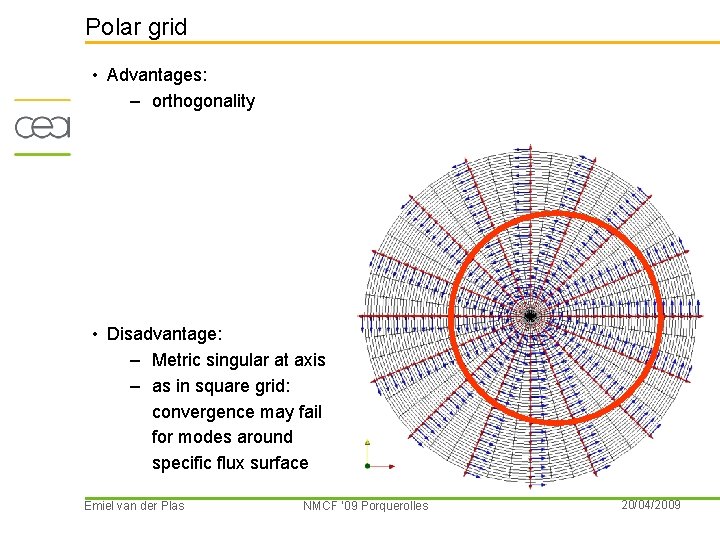
Polar grid • Advantages: – orthogonality • Disadvantage: – Metric singular at axis – as in square grid: convergence may fail for modes around specific flux surface Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

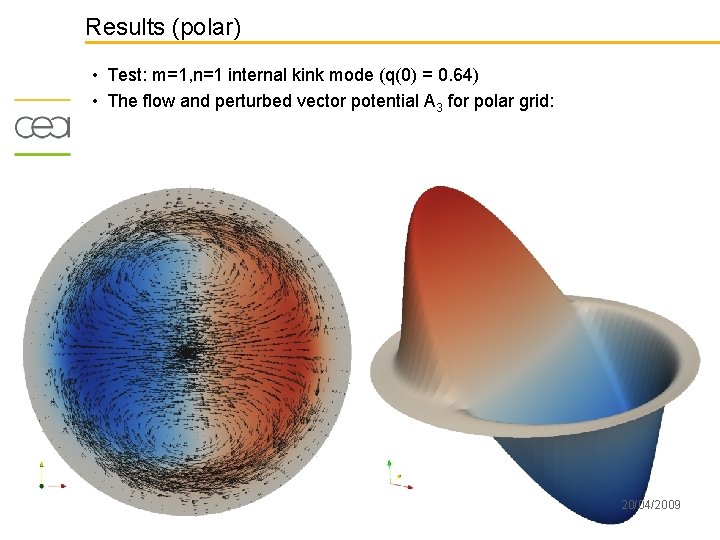
Results (polar) • Test: m=1, n=1 internal kink mode (q(0) = 0. 64) • The flow and perturbed vector potential A 3 for polar grid: Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

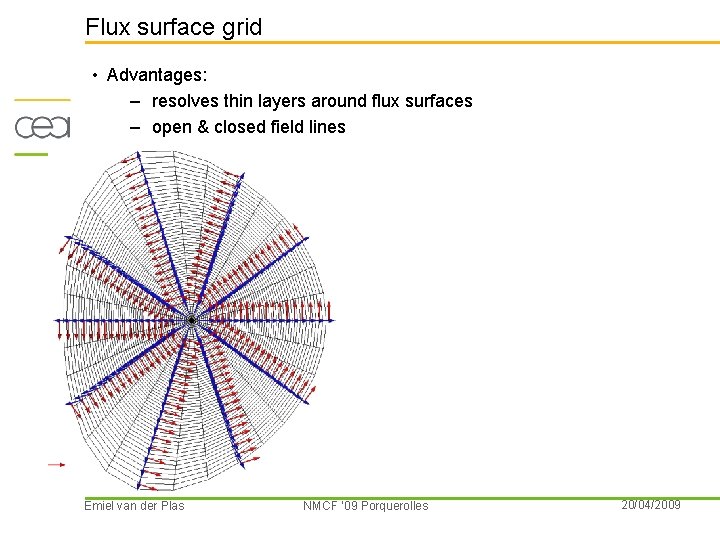
Flux surface grid • Advantages: – resolves thin layers around flux surfaces – open & closed field lines Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

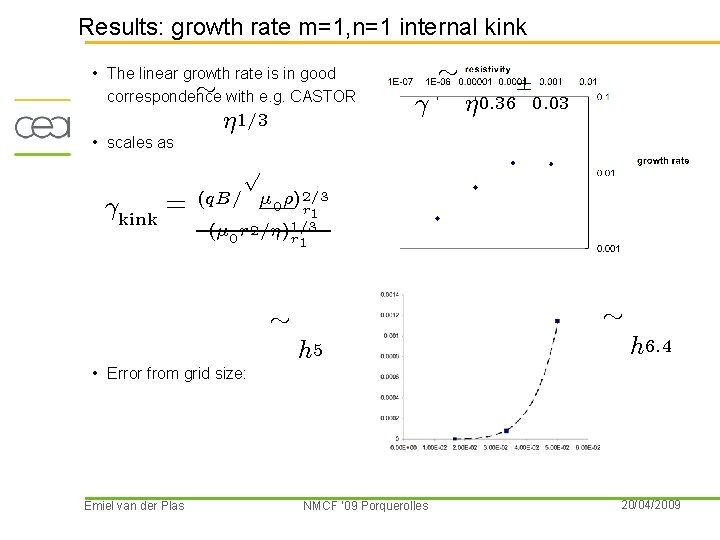
Results: growth rate m=1, n=1 internal kink • The linear growth rate is in good » with e. g. CASTOR correspondence • scales as ´ 1=3 ° » ´ 0: 36 § 0: 03 p °kink = (q. B= ¹ 0 ½)2=3 r 1 (¹ 0 r 2 =´)1=3 r 1 » • Error from grid size: Emiel van der Plas h 5 NMCF ’ 09 Porquerolles » h 6: 4 20/04/2009

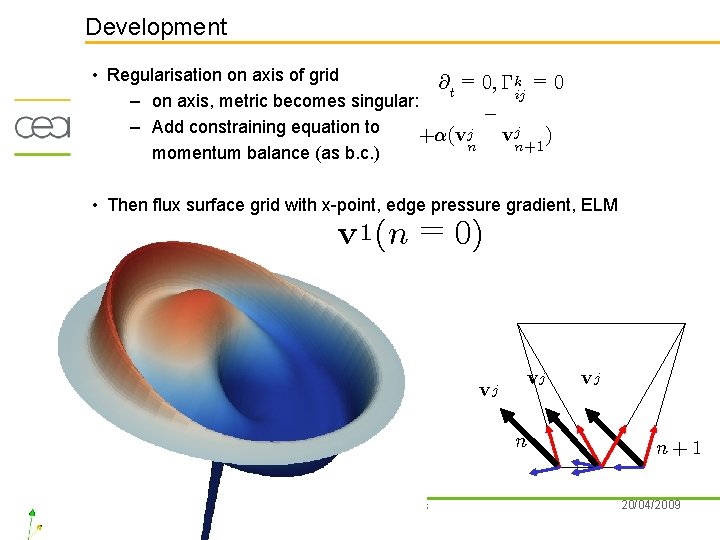
Development • Regularisation on axis of grid @t = 0; ¡k = 0 ij – on axis, metric becomes singular: ¡ – Add constraining equation to +®(vj vj ) n n+1 momentum balance (as b. c. ) • Then flux surface grid with x-point, edge pressure gradient, ELM v 1 (n = 0) vj vj n Emiel van der Plas NMCF ’ 09 Porquerolles vj n+1 20/04/2009

JOREK Collaborations • UKAEA, Ian Chapman : resistive wall modes – Implementation of a resistive wall – Coupling with the magnetic field outside vessel • FOM, Dirk Hoving (University Eindhoven/FOM): divertor model – Interaction plasma-neutrals (fluid model) • FOM, Egbert Westerhof : – Tearing Modes, stabilisation, application TEXTOR • Longer term subjects (2009 -2012): – Disruptions – Fast particles (FOM, J. W. Blokland) – Divertor model • Renewal ANR on MHD (2010? ) Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

Conclusion • project ASTER: model full ELM cycle • JOREK 2 in RMHD works ok • JOREK: full MHD – in quadrangular/polar grid quasi-linear kink mode • growth rate ´ • scaling under – under development: full nonlinear time evolution n=0 • vector representation at center Ce travail a bénéficié d'une aide de l'Agence Nationale de la Recherche portant (référence ANR-06 - CIS 6 -001). Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

Thank you Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

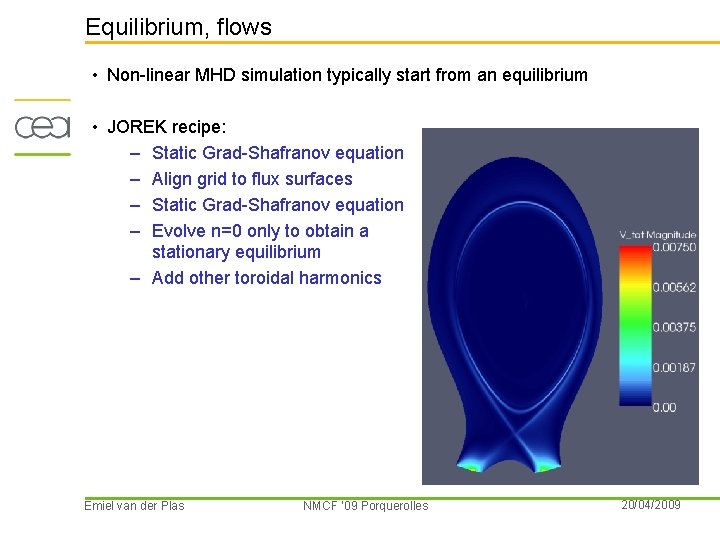
Equilibrium, flows • Non-linear MHD simulation typically start from an equilibrium • JOREK recipe: – Static Grad-Shafranov equation – Align grid to flux surfaces – Static Grad-Shafranov equation – Evolve n=0 only to obtain a stationary equilibrium – Add other toroidal harmonics Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

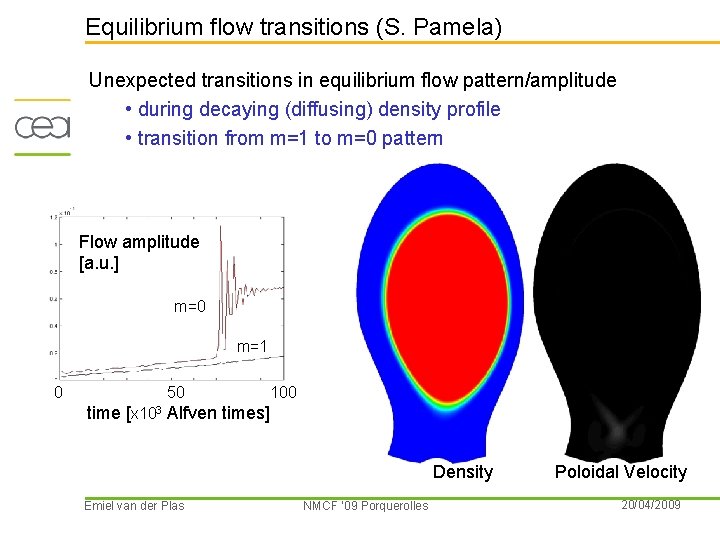
Equilibrium flow transitions (S. Pamela) Unexpected transitions in equilibrium flow pattern/amplitude • during decaying (diffusing) density profile • transition from m=1 to m=0 pattern Flow amplitude [a. u. ] m=0 m=1 0 50 100 time [X 103 Alfven times] Density Emiel van der Plas NMCF ’ 09 Porquerolles Poloidal Velocity 20/04/2009

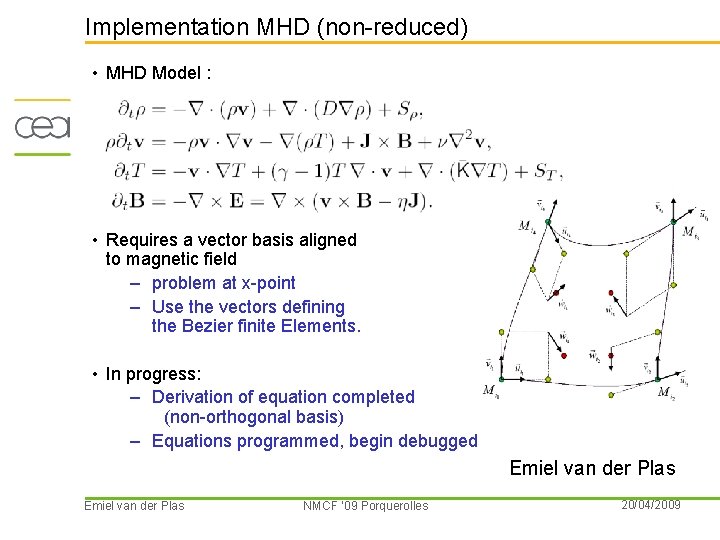
Implementation MHD (non-reduced) • MHD Model : • Requires a vector basis aligned to magnetic field – problem at x-point – Use the vectors defining the Bezier finite Elements. • In progress: – Derivation of equation completed (non-orthogonal basis) – Equations programmed, begin debugged Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK Ongoing activities (2008 -2009) • ELM physics studies (S. Pamela) • 2 -fluid MHD, Te, Ti, diamagnetic flows (S. Pamela) • Resonant magnetic field perturbations (M. Becoulet) • Full MHD implementation (E. van der Plas) • Fluid neutral model (D. Hoving) • Implementation external magnetic field (G. Huysmans) • Adaptive grid refinement (postdoc Bordeaux) Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK Equations reduced MHD • Formulation ¡ r using£electric and magnetic potentials: F v= R u(t) eÁ + vk(t)B; £ r 1 B = 0 eÁ + Ã(t) eÁ R R Poloidal flux Parallel momentum Poloidal momentum Temperature Density Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK Time stepping • Implementation of new time evolution scheme in JOREK 2: – Fully implicit, using iterative solution (GMRES) • Matrix for each toroidal harmonic used as preconditioner – Solved using Pasti. X or MUMPS (using N MPI groups, new option in Pasti. X) – Preconditioning only recalculated when GMRES requires too many iterations – Reduce time step when number of iterations still too large • Much improved scaling parallelisation/memory use – First tests on CCRT platine (up to 512 cores) – reasonable scaling when (n_tor / n_cpu) constant • To be compared with Pasti. X iterative/direct solution – Alternative : partially explicit scheme: • Each toroidal harmonic implicit (ignoring coupling between harmonics) • Coupling terms explicit • Scheme as in SFELES CFD code Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK 2 Non-linear MHD ELM Simulations • First simulations including parallel flow and Mach one boundary conditions at the divertor: – Ntor=0 -21 (periodicity 3) – Ncpu=128 (Norma) formation of density filaments Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

Non-linear MHD ELM Simulations • The non-linear MHD simulations (ballooning modes) are, qualitatively, in agreement with experimental observations: – Formation of filaments – Density profile perturbations (“density depression”) – Fine Structure in the power deposited at the divertor target temperature Emiel van der Plas density NMCF ’ 09 Porquerolles 20/04/2009

Power deposition profiles • Fine Structures (~cm) observed in the JOREK simulations are similar to the structures observed in the AUG divertor. Simulation Temperature at target Emiel van der Plas Measured heat flux (AUG) NMCF ’ 09 Porquerolles 20/04/2009

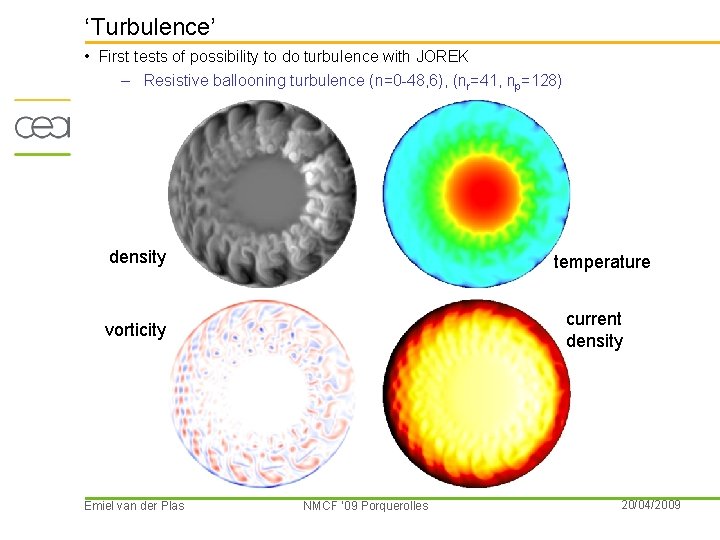
‘Turbulence’ • First tests of possibility to do turbulence with JOREK – Resistive ballooning turbulence (n=0 -48, 6), (nr=41, np=128) density temperature current density vorticity Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

JOREK 2 : real or complex • JOREK version using complex variables – Tearing mode test cases diverges after 105 Alfven times (in steady state with island) – Ballooning mode cases diverge in the early non-linear phase • using real variables – Stable for both tearing and ballooning mode cases – But slower for matrix construction/solution, larger memory requirements Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009

Implicit n=0 equation • Implicit complex scheme cannot be reduced to remove conjugate harmonics from the equation for n=0: – but conjugate variables not available • Implicit real scheme keeps all terms: Emiel van der Plas NMCF ’ 09 Porquerolles 20/04/2009