Lecture Planet Formation Topic Introduction to hydrodynamics and

Lecture “Planet Formation” Topic: Introduction to hydrodynamics and magnetohydrodynamics Lecture by: C. P. Dullemond

Equations of hydrodynamics Hydrodynamics can be formulated as a set of conservation equations + an equation of state (EOS). Equation of state relates pressure P to density and (possibly) temperature T In astrophysics: ideal gas (except inside stars/planets): For typical H 2/He mixture: Sometimes assume adiabatic flow: For H 2 (molecular): =7/5 For H (atomic): Sometimes assume given T (this is what we will do in this lecture, because often T is fixed to external temperature) =5/3

Equations of hydrodynamics Conservation of mass: Conservation of momentum: Energy conservation equation need not be solved if T is given (as we will mostly assume).

Equations of hydrodynamics Comoving frame formulation of momentum equation: Continuity equation So, the change of v along the fluid motion is:

Equations of hydrodynamics Momentum equation with (given) gravitational potential: So, the complete set of hydrodynamics equations (with given temperature) is:

Isothermal sound waves No gravity, homonegeous background density ( 0=const). Use linear perturbation theory to see what waves are possible So the continuity and momentum equation become:

Supersonic flows and shocks If a parcel of gas moves with v<cs, then any obstacle ahead receives a signal (sound waves) and the gas in between the parcel and the obstacle can compress and slow down the parcel before it hits the obstacle. If a parcel of gas moves with v>cs, then sound signals do not move ahead of parcel. No ‘warning’ before impact on obstacle. Gas is halted instantly in a shock-front and the energy is dissipated. Chain collision on highway: visual signal too slow to warn upcoming traffic.

Shock example: isothermal Galilei transformation to frame of shock front. (1) Continuity equation: Momentum conservation: (2) Combining (1) and (2), eliminating i and o yields: Incoming flow is supersonic: outgoing flow is subsonic:

Viscous flows Most gas flows in astrophysics are inviscid. But often an anomalous viscosity plays a role. Viscosity requires an extra term in the momentum equation Navier-Stokes Equation The tensor t is the viscous stress tensor: shear stress (the second viscosity is rarely important in astrophysics)

Magnetohydrodynamics (MHD) • Like hydrodynamics, but with Lorentz-force added • Mostly we have conditions of “Ideal MHD”: infinite conductivity (no resistance): – Magnetic flux freezing – No dissipation of electro-magnetic energy – Currents are present, but no charge densities • Sometimes non-ideal MHD conditions: – Ions and neutrals slip past each other (ambipolar diffusion) – Reconnection (localized events) – Turbulence induced reconnection

Ideal MHD: flux freezing Galilei transformation to comoving frame (’) ( infinite, but j finite) Galilei transformation back: Suppose B-field is static (E-field is 0 because no charges): Gas moves along the B-field

Ideal MHD: flux freezing More general case: moving B-field lines. A moving B-field is (by definition) accompanied by a E-field. To see this, let’s start from a static pure magnetic B-field (i. e. without E-field). Now move the whole system with some velocity u (which is not necessarily v): On previous page, we derived that in the comoving frame of the fluid (i. e. velocity v), there is no E-field, and hence: (Flux-freezing)

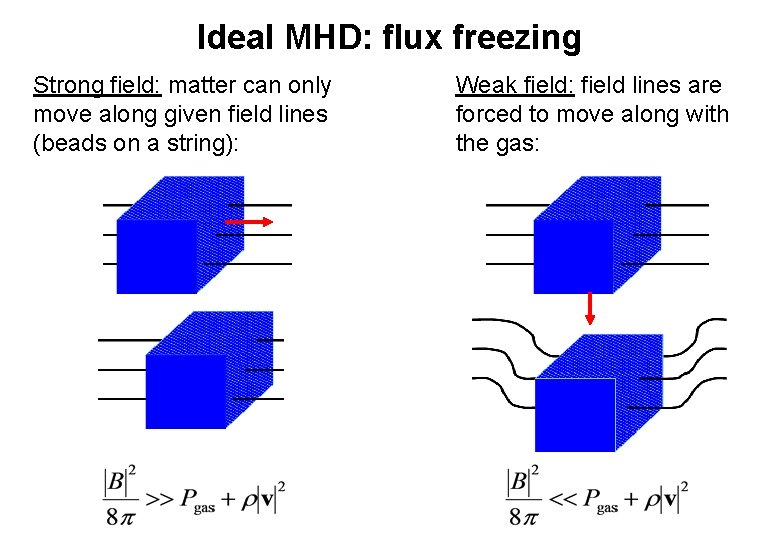
Ideal MHD: flux freezing Strong field: matter can only move along given field lines (beads on a string): Weak field: field lines are forced to move along with the gas:

Ideal MHD: flux freezing Coronal loops on the sun

Ideal MHD: flux freezing Mathematical formulation of flux-freezing: the equation of ‘motion’ for the B-field: Exercise: show that this ‘moves’ the field lines using the example of a constant v and gradient in B (use e. g. right-hand rule).

Ideal MHD: equations Ampère’s law: (in comoving frame) (Infinite conductivity: i. e. no displacement current in comoving frame) Momentum equation magneto-hydrodynamics: Lorentz force: Momentum equation magneto-hydrodynamics:

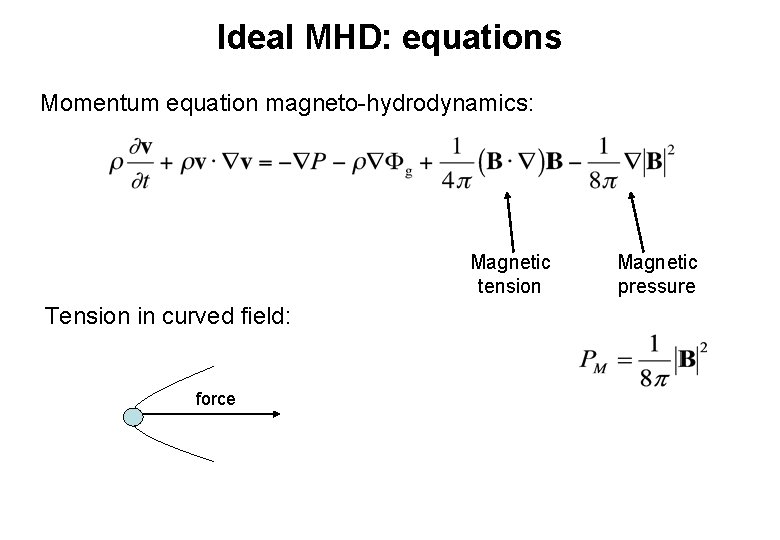
Ideal MHD: equations Momentum equation magneto-hydrodynamics: Magnetic tension Tension in curved field: force Magnetic pressure

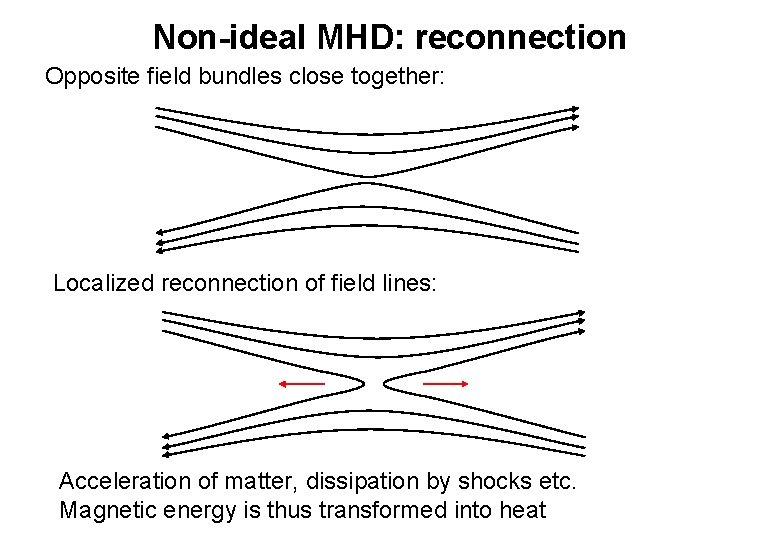
Non-ideal MHD: reconnection Opposite field bundles close together: Localized reconnection of field lines: Acceleration of matter, dissipation by shocks etc. Magnetic energy is thus transformed into heat