Lecture 4 MHD equations Flux Freezing The MHD










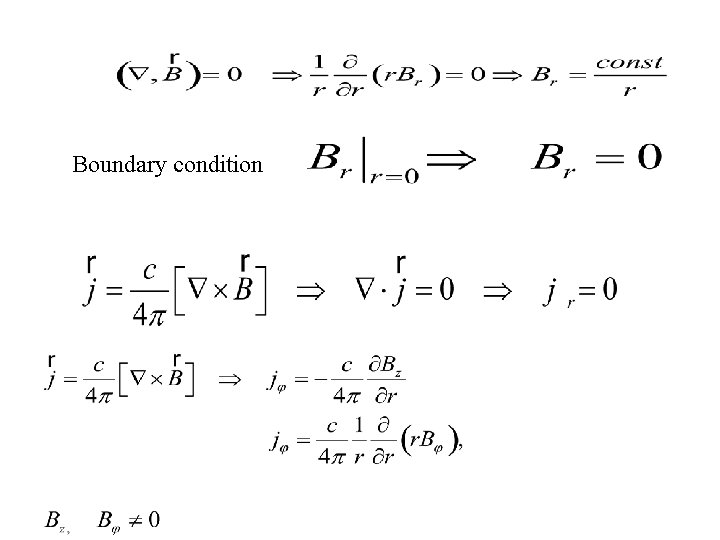




- Slides: 15

Lecture 4

MHD equations


Flux Freezing The MHD Ohm’s law is sometimes referred to as the perfect conductivity equation, for obvious reasons, and sometimes as the flux freezing equation. Local freezing in condition

Let us write the equation for liquid line. Each point of this line is connected with the particle. So this line moves together with the particles comprising the line. Let us investigate how the length of this line changes with time. It means that if at the initial moment these vectors coincide by direction, they will be parallel all the time, and their length will change proportionally. So if two infinitely close liquid elements are located on the same line of force they will stay on the same line. We conclude each magnetic field line moves together with liquid elements on it, or that magnetic field lines are frozen in plasma.

The magnetic flux through any closed contour in the plasma, each element of which moves with the local plasma velocity, is a conserved quantity. In order to verify the above assertion, let us consider the magnetic flux, Ψ, through a contour, C, which is co-moving with the plasma: Here, S is some surface which spans C. The time rate of change of Ψ is made up of two parts. Firstly, there is the part due to the time variation of B over the surface S. This can be written Using the Maxwell equation, this reduces to

Secondly, there is the part due to the motion of C. If dl is an element of C then V × dl is the area swept out by dl per unit time. Hence, the flux crossing this area is B・V × dl. It follows that Using Stokes’s theorem, we obtain Hence, the total time rate of change of Ψ is given by

The condition c. E + V × B = 0 clearly implies that Ψ remains constant in time for any arbitrary contour. This, in turn, implies that magnetic field-lines must move with the plasma. In other words, the field lines are frozen into the plasma. A flux-tube is defined as a topologically cylindrical volume whose sides are defined by magnetic field-lines. Suppose that, at some initial time, a flux-tube is embedded in the plasma. According to the flux-freezing constraint, the subsequent motion of the plasma and the magnetic field is always such as to maintain the integrity of the flux-tube. Since magnetic fieldlines can be regarded as infinitely thin flux-tubes, we conclude that MHD plasma motion also maintains the integrity of field lines. In other words, magnetic field-lines embedded in an MHD plasma can never break and reconnect: i. e. , MHD forbids any change in topology of the field-lines.

Equilibrium configurations in MHD

Unlimited plasma configuratios
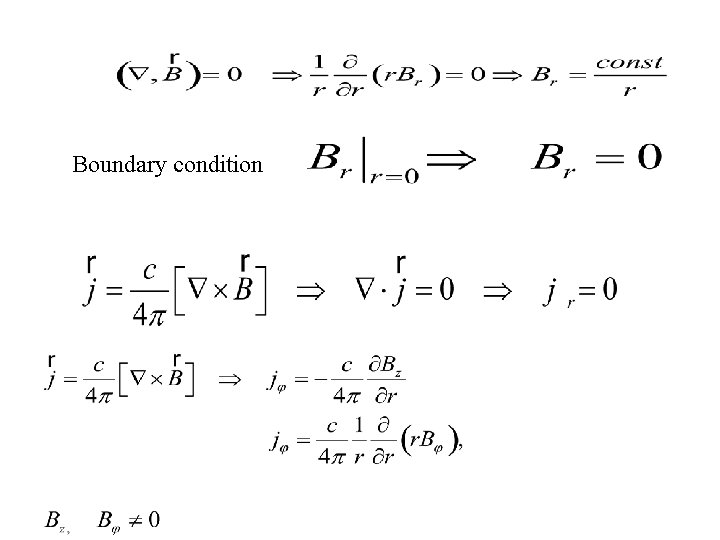
Boundary condition


MHD Shocks Consider a subsonic disturbance moving through a conventional neutral fluid. As is well known, sound waves propagating ahead of the disturbance give advance warning of its arrival, and, thereby, allow the response of the fluid to be both smooth and adiabatic. Now, consider a supersonic disturbance. In this case, sound waves are unable to propagate ahead of the disturbance, and so there is no advance warning of its arrival, and, consequently, the fluid response is sharp and non-adiabatic. This type of response is generally known as a shock. Let us investigate shocks in MHD fluids. In general, a shock propagating through an MHD fluid produces a significant difference in plasma properties on either side of the shock front. The thickness of the front is


 Mhd equations
Mhd equations Unit of magnetic flux density in weber
Unit of magnetic flux density in weber Magnetic retentivity
Magnetic retentivity 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Predominant cell type
Predominant cell type Mhd
Mhd Introduction to mhd
Introduction to mhd Mhd lm
Mhd lm What is the working fluid in closed cycle mhd system?
What is the working fluid in closed cycle mhd system? Mhd
Mhd Mhd alyssa
Mhd alyssa Mhd title
Mhd title 9-3 polar and rectangular forms of equations
9-3 polar and rectangular forms of equations Translate word equations to chemical equations
Translate word equations to chemical equations Expansion upon freezing
Expansion upon freezing Tunnel liquid nitrogen freezer
Tunnel liquid nitrogen freezer