MTODOS NUMERICOS PARA SOLUCION DE ECUACIONES Parte 2

MÉTODOS NUMERICOS PARA SOLUCION DE ECUACIONES Parte 2 JESUS_SUNIAGA | 26 DE OCTUBRE DE 2016

CONTENIDO Teorema de BOLZANO METODO DE LA BISECCION Es un algoritmo de búsqueda de raíces que trabaja dividiendo el intervalo a la mitad y seleccionando el subintervalo que tiene la raíz. Este es uno de los métodos más sencillos y de fácil intuición para resolver ecuaciones en una variable. Se basa en el teorema de BOLZANO Sea y = f(x) continua en un intervalo [a, b] y supongamos que f(x) tenga signos opuestos en a y b es decir f(a)*f(b)<0 Entonces debe existir r en [a, b] tal que f(r)=0, es decir, debe haber por lo menos una raíz en el intervalo

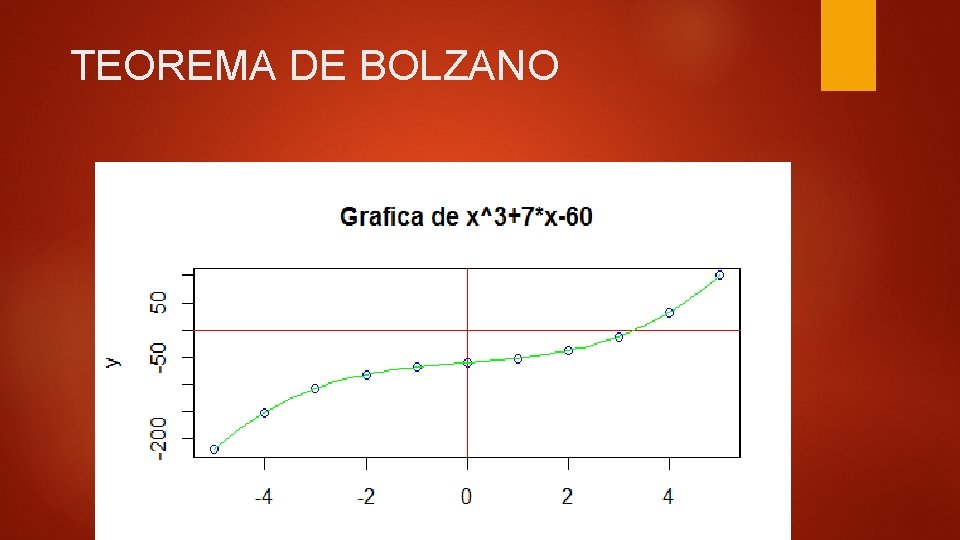
TEOREMA DE BOLZANO

PROGRAMA PARA DETECTAR VLORES DE a y b tal que f(a)*f(b)<0 y<-function(x) x^3+7*x-60 for(x in -100: 100) {z<-y(x)*y(x+1) if(z<0) {cat ("cambio de signo detectado entre ", x , "y", x+1) stop()} cambio de signo detectado entre 3 y 4 y(3)=-12, y(4)=32

Algoritmo i) Encontrar valores iniciales xa y xb, tales que y tienen signos opuestos ii ) La primera aproximación a la raíz se toma igual al punto medio entre xa y xb es decir Xm=(x 1+x 2)/2 iii) Evaluar f(xm). Forzosamente debemos caer en uno de los siguientes casos: primero: f(xm)*f(xa)>0. En este caso, f(xa) y f(xm) tienen el mismo signo. Por lo tanto, la raíz se encuentra en el intervalo [xm, xb] segundo: f(xm)*f(xa)<0 En este caso, f(xa) y f(xm) tienen signos opuestos, y por lo tanto la raíz se encuentra en el intervalo [xa, xm] . tercero: f(xm)*f(xa)=0 En este caso se tiene que f(xm)=0 y por lo tanto ya localizamos la raíz que es xm i. V Repetir paso iii con el nuevo intervalo, hasta que la raiz hallada sea menor que una tolerancia especificada es decir hasta que abs(f(xm))<e

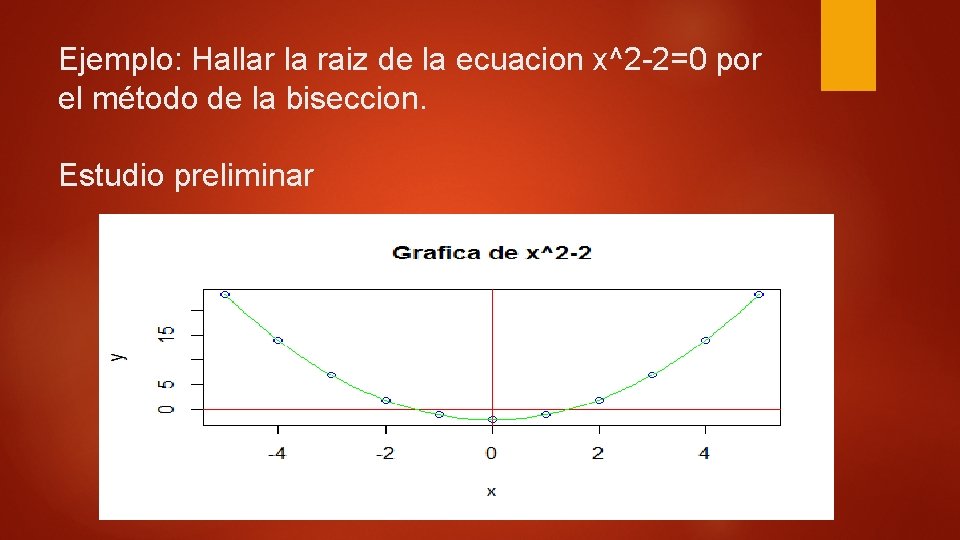
Ejemplo: Hallar la raiz de la ecuacion x^2 -2=0 por el método de la biseccion. Estudio preliminar -----

y(1) [1] -1 > y(2) [1] 2 Programa para detectar puntos de inicio for(x in 0: 4) {z<-y(x)*y(x+1) if(z<0) {cat ("cambio de signo detectado entre ", x , "y", x+1) stop()}} cambio de signo detectado entre 1 y 2 y(1)=-1, y(2)=2 c a m b i o y<-function(x) x^2 -2 d e s i g n o d e t e c t a d o e n t r e 1 y 2

Solución i) Calculamos el punto medio (que es de hecho nuestra primera aproximación a la raíz) iii) Repetimos el proceso con el nuevo intervalo [1, 2]. Calculamos el punto medio (que es nuestra segunda aproximación a la raíz): xm=(1+2)/2 =1. 5 Evaluamos f(1. 5)=0. 25 cambia b, a queda igual. la raíz se encuentra en el intervalo [1, 1. 5] El grafico siuiente nos permite visualizar los cambios: xm=(0+2)/2 =1 ii) Evaluamos f(xm) =f(1)=-1 cambiamos a, a=1, b queda igual Este grafico nos permite visualizar los cambios: signo de f(x) - - + signo de f(x) ------ - + + 0 1 2 ------ Por lo tanto, vemos que la raíz se encuentra en el intervalo [1, 2]. En este punto, vemos que todavía no podemos calcular ningún error aproximado, puesto que solamente tenemos la primera aproximación. 1 1. 5 2 Aquí podemos calcular el primer error aproximado, puesto que contamos ya con la aproximación actual y la aproximación previa: e 1=|1. 5 -1| =0. 5

Continuación del ejemplo Iii-2)Repetimos el proceso con el nuevo intervalo [1, 1. 5] xm=1. 25 Iii-3 Repetimos el proceso ahora con el nuevo intervalo [1. 25, 1. 5] xm=1. 375 Evaluamos f(1. 25)=-0. 4375, cambia a, b queda igual. la raíz se encuentra en el intervalo [1. 25, 1. 5] Evaluamos f(1. 375)=-0. 1. 09375, cambia a, b queda igual. la raíz se encuentra en el intervalo [1. 375, 1. 5] El grafico correspondiente en esta etapa: El grafico correspondiente es signo de f(x) - - + - - + ----------------- 1. 25 1. 5. 1. 25 1. 375 1. 5 Calculam el error err=|1. 25 -1. 51 =0. 25 err=|1. 375 -1. 251 =0. 125 El proceso debe seguirse hasta cumplir el objetivo

. Tabla Resumen: Aprox. Error aprox. 1 1. 5 0. 5 1. 25 0. 25 1. 375 0. 125 1. 4375 0. 0625 Así, obtenemos como aproximación a la raíz 1. 4375 P á T g e oi H n orl érr a e a f or w n i e o e b o l d e c e tll r t órti n ar a si b b ct a a orj

# PROGRAMA EN R # Metodo de Biseccion #valores iniciales a=0; b=2; N=20; E=0. 01 #definimos la funcion f = function(x) x^2 -2 #dibujo curve(f, from=-5, to=5, col="red") abline(h=0, col="blue")

Programa continuacion #CICLO ITERACTIVO XANT=0 FOR ( I IN 1: N){ XM=(A+B)/2 ERR=ABS(XM-XANT) CAT("N", "ITERACION", I) CAT("N", "A, B, XM", A, B, XM, "IMAGENES", F(A), F(B), F(XM), "N", "RAIZ=", XM, "ERROR =", ERR) IF(ABS(F(XM))<E) {CAT("N", "CONVERGE EN", I, "ITERACIONES", "RAIZ = ", XM) STOP()} ELSE{ IF (F(A)*F(XM)> 0) {A = XM; PRINT("CAMBIA A, B QUEDA IGUAL ") } IF (F(A)*F(XM)< 0) {B = XM; PRINT("CAMBIA B, A QUEDA IGUAL ")} } XANT=XM }

METODO DE LA REGLA FALSA EL MÉTODO DE REGLA FALSA O FALSA POSICIÓN ES UN MÉTODO ITERATIVO DE RESOLUCIÓN NUMÉRICA DE ECUACIONES NO LINEALES MUY SIMILAR AL MÉTODO DE LA BISECCIÓN EXCEPTO QUE EN CADA PASO EN LUGAR DE USAR EL PUNTO MEDIO SE USA LA INTERSECCIÓN DE LA RECTA QUE UNE LOS EXTREMOS DEL INTERVALO CON EL EJE X

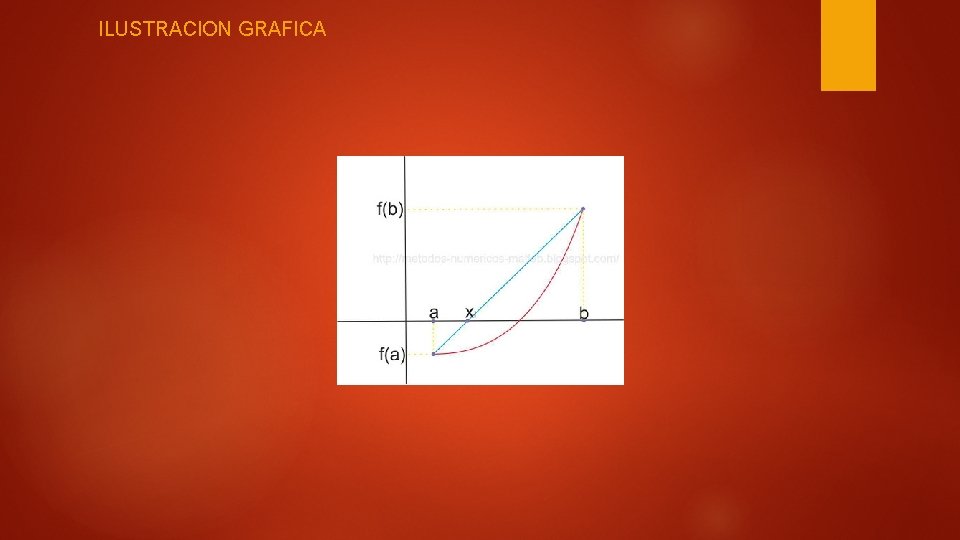
ILUSTRACION GRAFICA

ALGORITMO Nota: Como se dijo antes la única diferencia es la formula de calculo de la raíz aproximada que en el caso del método de la bisección es el punto medio, xm=(xa+xb) en el caso del método de la regla falsa la raiz xm se calcula por la siguiente formula xm=[xb*f(xa)-xa*f(xb)]/[f(xa)-f(xb)] por lo tanto se puede reescribir el algoritmo del método de la Reglea Falsa parafreseando el Algoritmo de la Bisección

Algoritmo del método Regla Falsa i) Encontrar valores iniciales xa y xb, tales que y tienen signos opuestos ii ) La primera aproximación a la raíz se toma igual al punto xm dado por xm=[xb*f(xa)-xa*f(xb)]/[f(xa)-f(xb)] iii) Evaluar f(xm). Forzosamente debemos caer en uno de los siguientes casos: primero: f(xm)*f(xa)>0 En este caso, f(xa) y f(xm) tienen el mismo signo. Por lo tanto, la raíz se encuentra en el intervalo [xm, xb] segundo: f(xm)*f(xa)<0 En este caso, f(xa) y f(xm) tienen signos opuestos, y por lo tanto la raíz se encuentra en el intervalo [xa, xm]. tercero: f(xm)*f(xa)=0 En este caso se tiene que f(xm)=0 y por lo tanto ya localizamos la raíz.

ALGORITMO - CONTINUACION iv) El proceso se vuelve a repetir con el nuevo intervalo, hasta que la raiz hallada sea menor que una tolerancia especificada es decir hasta que abs(f(xm))<e Ejemplo: Sea la ecuación f(x)=x^0. 5 -cos(x) =0. Resolver por el metodo de la falsa posicion

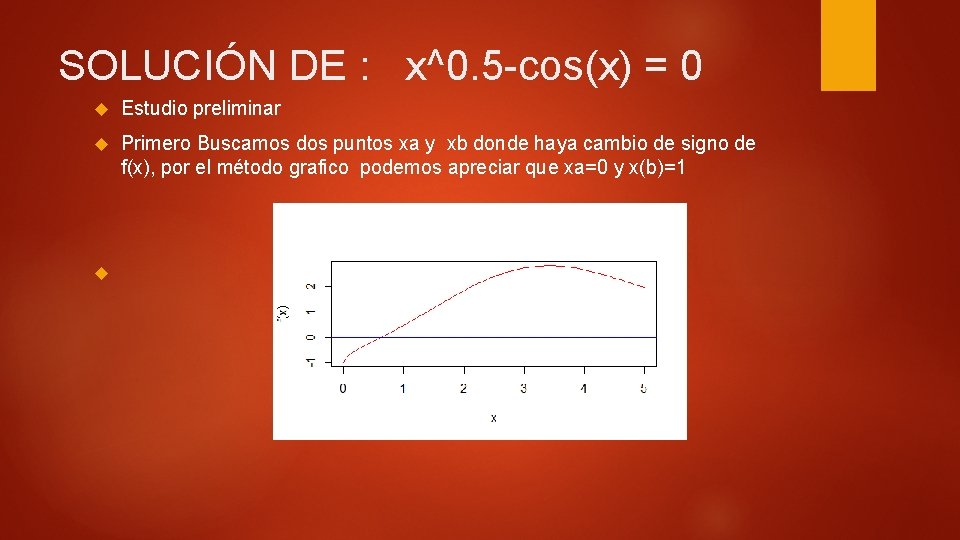
SOLUCIÓN DE : x^0. 5 -cos(x) = 0 Estudio preliminar Primero Buscamos dos puntos xa y xb donde haya cambio de signo de f(x), por el método grafico podemos apreciar que xa=0 y x(b)=1

SOLUCION-ESTUDIO PRELIMINAR programa para detectar raices y=function(x) x^0. 5 -cos(x); z=0 for(x in 0: 5) {z<-y(x)*y(x+1) if(z<0) {cat (“cambio de signo detectado entre “, x , ”y”, x+1) stop()} } corrida: cambio de signo detectado entre 0 y 1 => f(0)=-1 y f(1)=0. 46

SOLUCION- PASO 1 1) Iteración inical, xa=0, xb=1 Calculamos xm xm=[xb*f(xa)-xa*f(xb)]/[f(xa)-f(xb)] =(1*f(0)-0)/(f(0)-f(1))= 0. 685 Evaluamos f(xm) => f(. 685)=0. 053 signo de f(x) – + + ———– => La raiz se encuentra en el intervalo [0, 0. 68] 0 0. 68 1

SOLUCION – PASO 2 2)Segunda Iteración xa=0; xb=0. 68 ; f(0)=-1 f(0. 68)=0. 047 xm=[xb*f(xa)-xa*f(xb)]/[f(xa)-f(xb)] =(0. 68*f(0)-0)/(f(0)-f(0. 68))=0. 649 Evaluamos f(xm) => f(. 649)=0. 009. Err 1=abs(0. 649 -0. 685)=0. 036 signo de f(x) – + + ———– — => La raiz se encuentra en el intervalo [0, 0. 649] 0 0. 649 0. 68

SOLUCION – PASO III Tercera Iteración xa=0; xb=0. 649 xm=[xb*f(xa)-xa*f(xb)]/[f(xa)-f(xb)] =(0. 649*f(0)-0)/(f(0)-f(0. 649))=0. 643 Evaluamos f(xm) => f(. 643)=0. 009. Err 1=abs(0. 649 -0. 685)=0. 0015 signo de f(x) – + + ———– — => La raiz se encuentra en el intervalo [0, 0. 643] 0 0. 643 0. 649 Err 2=abs(0. 643 -0. 649)=0. 06

TABLA DE RESULTADOS Tabla de resultados Aprox. Error aprox. 0. 685 0. 649 0. 036 0. 643 0. 0015

PROGRAMA METODO REGLA FALSA ## Metodo de Regla Falsa #valores iniciales a=0; b=1; N=20; E=0. 001 #definimos la funcion f = function(x) x^0. 5 -cos(x) #dibujo curve(f, from=0, to=5, col=”red”) abline(h=0, col=”blue”) # chequeo del teorema de bolzano if (f(a)*f(b) > 0) { cat(“error: f(xmin) y f(xmax) son del mismo signo. Escoja otro par de valores”) stop()}

PROGRAMA-CICLO ITERATIVO xant=0 for ( i in 1: N){ xm=(b*f(a)-a*f(b))/(f(a)-f(b)) err=abs(xm-xant) cat(“n”, ”iteracion”, i) cat(“n”, ”a, b, xm”, a, b, xm, ”imagenes”, f(a), f(b), f(xm), “n”, “raiz=”, xm, “error =”, err) if(abs(f(xm))<E) {cat(“n”, ”converge en”, i, ”iteraciones”, “raiz = “, xm) stop()} else{ if (f(a)*f(xm)> 0) {a = xm; print(“cambia a, b queda igual “) } if (f(a)*f(xm)< 0) {b = xm; print(“cambia b, a queda igual “)} } xant=xm }

CORRIDA iteracion 1 a, b, xm 0 1 0. 6850734 imagenes -1 0. 4596977 0. 05331895 raiz= 0. 6850734 error = 0. 6850734[1] “cambia b, a queda igual ” iteracion 2 a, b, xm 0 0. 6850734 0. 650395 imagenes -1 0. 05331895 0. 01062599 raiz= 0. 650395 error = 0. 03467838[1] “cambia b, a queda igual ” iteracion 3 a, b, xm 0 0. 650395 0. 6435566 imagenes -1 0. 01062599 0. 002253033 raiz= 0. 6435566 error = 0. 006838428[1] “cambia b, a queda igual ” iteracion 4 a, b, xm 0 0. 6435566 0. 6421099 imagenes -1 0. 002253033 0. 0004835998 raiz= 0. 6421099 error = 0. 001446694 converge en 4 iteraciones raiz = 0. 6421099

DEDUCCION DE LA FORMULA

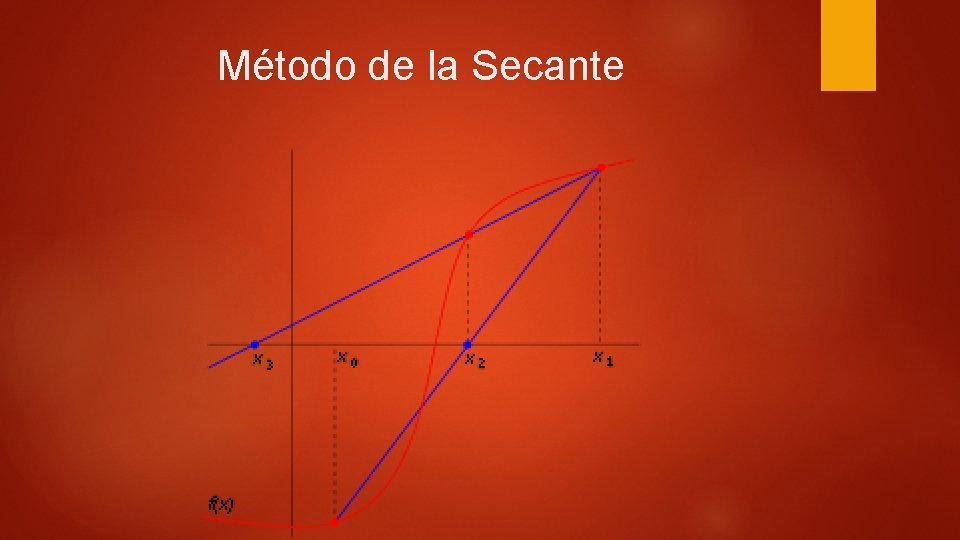
Metodo de la secante Es una variación del método de Newton-Raphson donde en vez de calcular la derivada de la función en el punto de estudio, se usa una aproximación de la derivada, Este método es de especial interés cuando es difícil derivar la función de estudio, por lo que el método de Newton no resulta atractivo. La aproximación a la derivada que usamos es: Df=(f(x 1)-f(x 0))/(x 1 -x 0). La que representa la pendiente de la recta secante que une los puntos (x 0, f(x 0)) y (x 1, f(x 1))

Método de la Secante

Programa de newton y de la secante #Metodo de Newton para resolver x^2 -2=0 #Metodo de la Secante para resolver x^2 -2=0 f=function(x) x^2 -2 f= function(x) x^2 -2 tol=0. 001; n=20 x 0=1; x 1=2; tol=0. 001; n=20 x 0= 1 for(i in 1: n) { x=x 0 - f(x 0)/df(x 0) aprox. df=(f(x 1)-f(x 0))/(x 1 -x 0) print(c(i, x 0, f(x 0))) x=x 0 - f(x 0)/aprox. df error=abs(x-x 0); print(c(i, x, error)) if (error<tol){ cat("n", "convergencia alcanzada if (error<tol){ cat("n", "convergencia en", i, " iteraciones", "raiz=", x) en iteraciones", i, "raiz", x) stop() } x 0=x 1; x 1=x x 0=x } print("maximo numero de iteraciones alcanzadas")

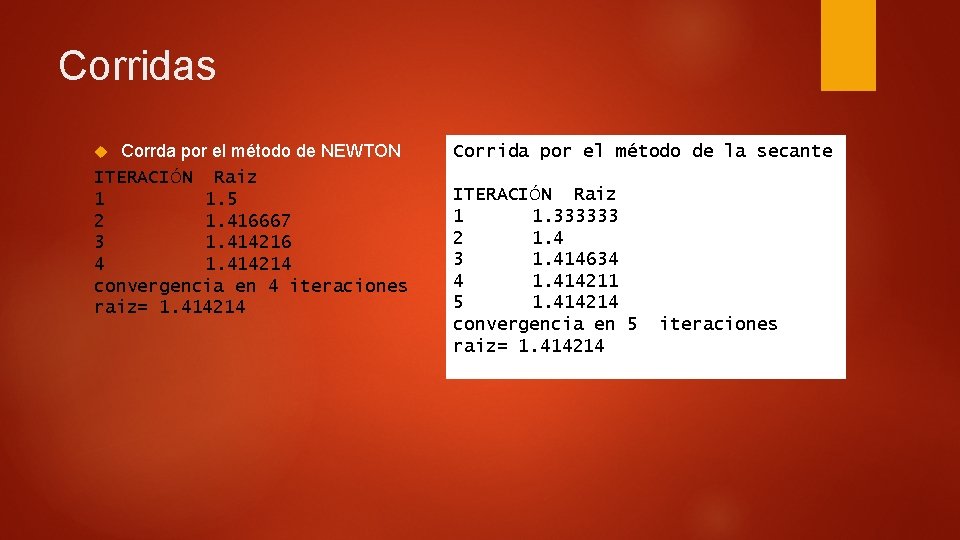
Corridas Corrda por el método de NEWTON ITERACIÓN Raiz 1 1. 5 2 1. 416667 3 1. 414216 4 1. 414214 convergencia en 4 iteraciones raiz= 1. 414214 Corrida por el método de la secante ITERACIÓN Raiz 1 1. 333333 2 1. 4 3 1. 414634 4 1. 414211 5 1. 414214 convergencia en 5 raiz= 1. 414214 iteraciones