Mtodos Numricos e Estatsticos Prof Marcone Jamilson Freitas

Métodos Numéricos e Estatísticos Prof. Marcone Jamilson Freitas Souza Aula 7: Métodos numéricos para equações diferenciais • 1 a ordem • Passos múltiplos • 2 a ordem REDEMAT - Métodos Numéricos e Estatísticos 1

Equações diferenciais de 1 a ordem Métodos numéricos são usados quando não é possível obter uma solução geral, ou a forma dela é tão complicada que seu uso não é prático. Uma equação diferencial de 1 a ordem tem a forma , e em geral podemos escrevê-la como: REDEMAT - Métodos Numéricos e Estatísticos Problema do valor inicial - uma equação diferencial - uma condição que deve ser satisfeita pela solução 2

Os métodos que estudaremos partem da idéia de que o espaço da variável independente (x) pode ser discretizado, formando uma rede x 0 x 1= x 0+h x 2= x 1+h. . . . h é o passo. O valor da função em cada ponto da rede é calculado a partir de expansões em série de Taylor. REDEMAT - Métodos Numéricos e Estatísticos 3

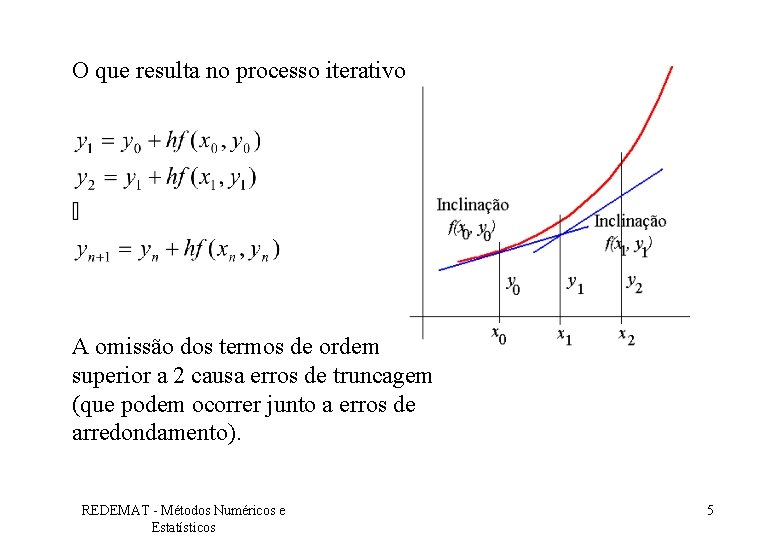
Método de Euler ou Euler-Cauchy O valor de y para um passo h é dado pela expansão: Como em geral h é pequeno, suprimimos os termos de ordem O(h 2): h 2, h 3, . . . Resultando na aproximação REDEMAT - Métodos Numéricos e Estatísticos 4

O que resulta no processo iterativo A omissão dos termos de ordem superior a 2 causa erros de truncagem (que podem ocorrer junto a erros de arredondamento). REDEMAT - Métodos Numéricos e Estatísticos 5

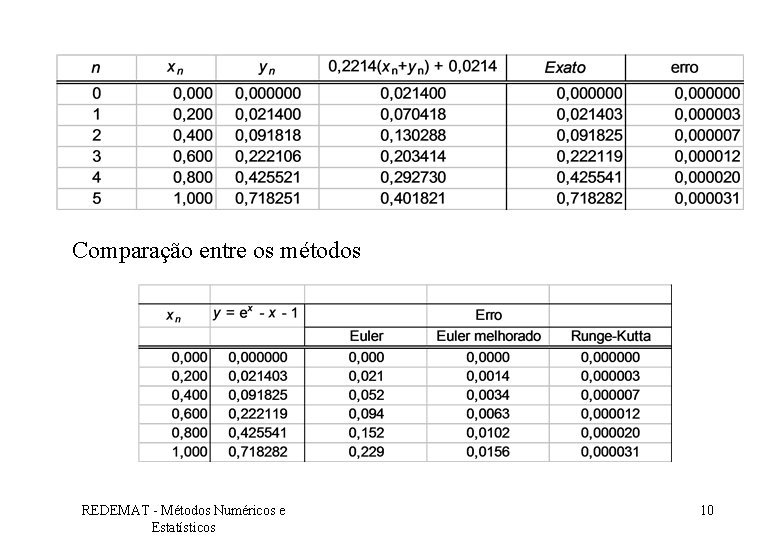
Exemplo: passo h=0, 2 O erro não é (em geral) conhecido. Podemos estimá-lo utilizando um passo h´=2 h REDEMAT - Métodos Numéricos e Estatísticos 6

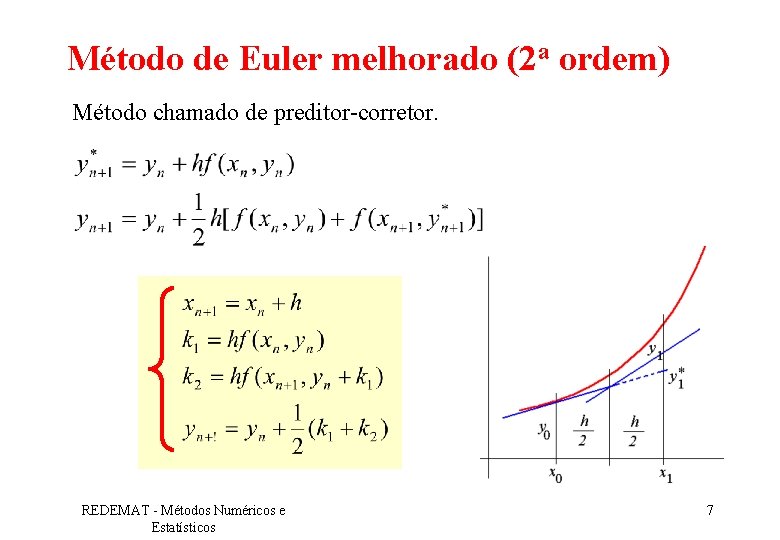
Método de Euler melhorado (2 a ordem) Método chamado de preditor-corretor. REDEMAT - Métodos Numéricos e Estatísticos 7

Exemplo: o mesmo visto anteriormente REDEMAT - Métodos Numéricos e Estatísticos 8

Método de Runge-Kutta (4 a ordem) Se f(x, y) não depender de y, o método reduz-se à regra de integração de Simpson REDEMAT - Métodos Numéricos e Estatísticos 9

Comparação entre os métodos REDEMAT - Métodos Numéricos e Estatísticos 10

Qual o valor mais adequado para o passo h? Se a função f varia muito com y, então h deve ser pequeno, para evitar erros de truncagem. Em geral, adota-se a “proposta” de que h h/2 se K 0, 05 h 2 h se 0, 01 K h não muda se 0, 05 K 0, 01 Estimativa de erro: REDEMAT - Métodos Numéricos e Estatísticos 11

Métodos para eq. dif. de segunda ordem P. V. I. Novamente o problema é obter os valores de yn´ para a seqüência x 1 = x 0 + h; x 2 = x 0 + 2 h; . . . Começamos mais uma vez pelas expansões em série de Taylor da função e de sua derivada: REDEMAT - Métodos Numéricos e Estatísticos 12

O método mais simples consiste em desprezar os termos em derivadas de ordem y´´´ ou superiores 1 o passo: REDEMAT - Métodos Numéricos e Estatísticos 2 o passo: 13

Runge-Kutta-Nyström Valores iniciais: x 0, y 0´ passo h Saída REDEMAT - Métodos Numéricos e Estatísticos 14

Equações diferenciais parciais Uma equação é dita quasilinear se for linear nas derivadas mais altas: REDEMAT - Métodos Numéricos e Estatísticos 15

Equações de diferenças para Eq. de Laplace e Poisson Vamos ver o caso mais simples em duas dimensões (x e y): Laplace Poisson (x, y+k) h (x-h, y) k k h (x, y) (x+h, y) (x, y-k) REDEMAT - Métodos Numéricos e Estatísticos 16

(x, y+k) h (x-h, y) k k h (x, y) (x+h, y) (x, y-k) REDEMAT - Métodos Numéricos e Estatísticos 17

Para as derivadas segundas, desprezando os termos O(h 4), temos Juntando as aproximações das derivadas primeiras e segundas, fazendo h=k, obtemos a equação de diferenças correspondente à equação de Poisson: REDEMAT - Métodos Numéricos e Estatísticos 18

Para f(x, y) = 0 temos a equação de Laplace. h é chamado de o comprimento da malha (mesh size). Equações elípticas - em geral - devem levar em conta problemas de contorno (condições previamente definidas numa dada fronteira espacial, por exemplo). Casos mais comuns: Fronteira C • Dirichlet: se u é definido na fronteira C • Neumann: se un= u/ n (derivada na direção normal) é definida na fronteira. Para resolver o problema, é necessário criar uma malha. : nós da rede ou da malha (Pij) REDEMAT - Métodos Numéricos e Estatísticos 19

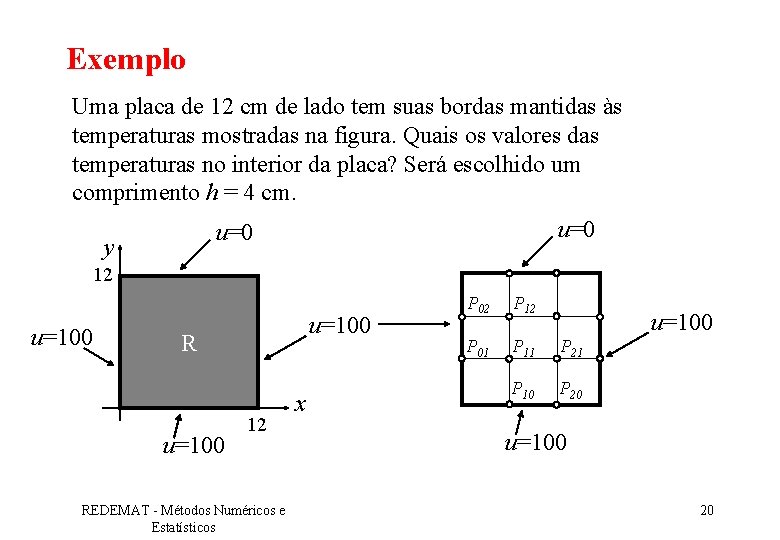
Exemplo Uma placa de 12 cm de lado tem suas bordas mantidas às temperaturas mostradas na figura. Quais os valores das temperaturas no interior da placa? Será escolhido um comprimento h = 4 cm. u=0 y 12 u=100 R u=100 12 REDEMAT - Métodos Numéricos e Estatísticos x P 02 P 12 P 01 P 11 P 21 P 10 P 20 u=100 20

A equação de transferência de calor é ut = c 2(uxx+uyy) ui-1, j Para o regime estacionário ut = 0, a equação se reduz à de Laplace uxx+uyy = 0 Para cada ponto da malha, temos a seguinte equação: ui, j+1 ui, j ui+1, j ui, j-1 ui+1, j + ui-1, j + ui, j+1 + ui, j-1 -4 ui, j = 0 P 11: - 4 u 11 + u 21 + u 01 + u 12 + u 10 = 0 - 4 u 11 + u 21 + 100 + u 12 + 100 = 0 - 4 u 11 + u 21 + u 12 = - 200 REDEMAT - Métodos Numéricos e Estatísticos 21

- 4 u 11 + u 21 + u 12 u 11 - 4 u 21 u 11 u 21 = -200 + u 22 = -200 - 4 u 12 + u 22 = -100 +u 12 = -100 - 4 u 22 Dando como resultados u 11 = u 21 = 87, 5 (88, 1) u 12 = u 22 = 62, 5 (61, 9) REDEMAT - Métodos Numéricos e Estatísticos 22