Matemticas clase 1 Nivelacin Conjuntos numricos Diagrama representativo

Matemáticas clase 1: Nivelación

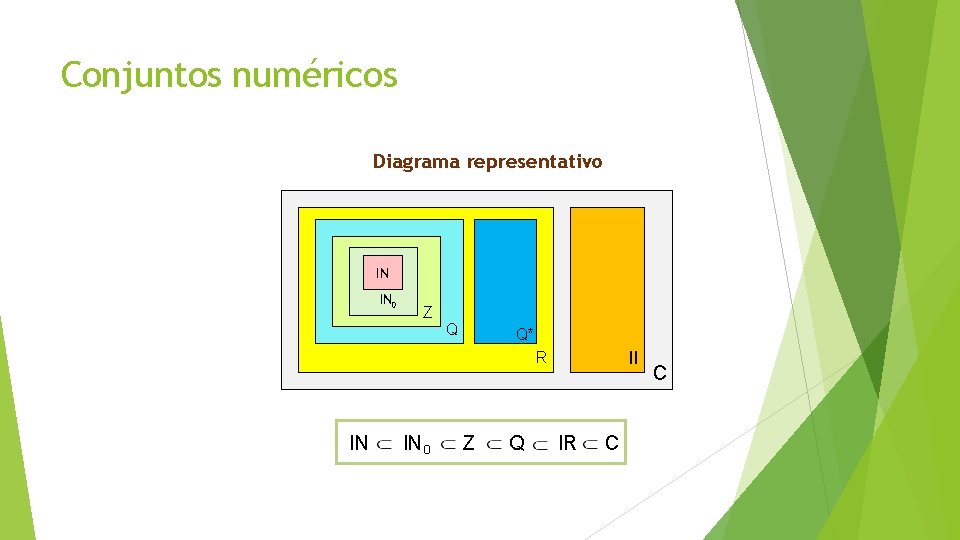
Conjuntos numéricos Diagrama representativo IN IN 0 Z Q Q* II R IN IN 0 Z Q IR C C

Conjuntos numéricos • Naturales: IN = {1, 2, 3, 4, 5, …} • Cardinales: IN 0 = {0, 1, 2, 3, 4, 5, …} • Enteros: Z = {…, – 3, – 2, – 1, 0, 1, 2, 3, …} • Racionales: Q= a / a y b son enteros, y b es distinto de cero b • Irracionales: Q* = • Imaginarios: II = {─ i, ─ 2 i, 3 i, …} • Complejos: C = {─ 3 ─ i, 176, …} i: unidad imaginaria, cuyo valor es

Propiedades Si a, b y c son números reales, entonces se cumplen las siguientes propiedades: Conmutatividad a+b=b+a a∙b=b∙a Asociatividad a + (b + c) = (a + b) + c Distributividad a ∙ (b + c) = a ∙ b + a ∙ c Elemento neutro aditivo a+0=0+a=a a ∙ (b ∙ c) = (a ∙ b) ∙ c a ∙ (b – c) = a ∙ b – a ∙ c

Propiedades Elemento neutro multiplicativo a∙ 1=1∙a=a Elemento absorbente de la multiplicación a∙ 0=0∙a=0 Inverso aditivo (opuesto) El inverso aditivo (opuesto) de a es (– a) Inverso multiplicativo (recíproco) Si a ≠ 0, el inverso multiplicativo (recíproco) de a es

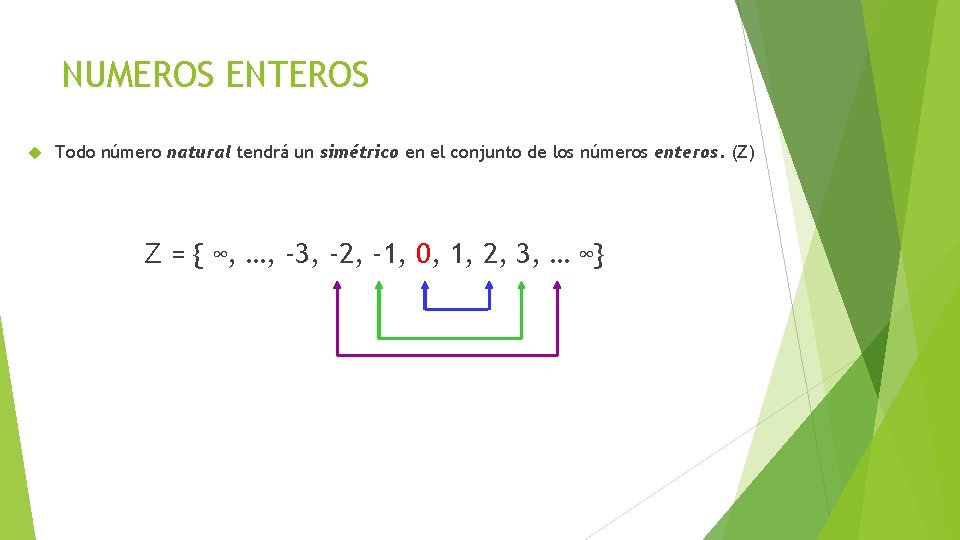
NUMEROS ENTEROS Todo número natural tendrá un simétrico en el conjunto de los números enteros. (Z) Z = { ∞, …, -3, -2, -1, 0, 1, 2, 3, … ∞}

Operaciones en Z Al realizar sumas, restas, multiplicaciones y divisiones en los enteros, debemos considerar algunas reglas con respecto a los signos: Si a y b son números entonces, se cumple que: a) a + -b = a – b Ejemplo: 5 + - 9 = 5 – 9 = -4 b) a – (-b) = a + b Ejemplo: 12 – (-8) = 12 + 8 = 20

c) Al sumar enteros de igual signo, éste se mantiene. Ejemplo: 25 + 8 = +33 -5 + - 9 = -14 d) Al sumar enteros de distinto signo, se calcula la diferencia entre sus valores absolutos, conservando el signo del mayor. Ejemplo: -10 + 7 = -3 75 + -9 = +66

e) Si a y b son dos números enteros de igual signo (positivos o negativos), entonces: - El producto y el cuociente entre ellos es positivo. Ejemplo: -42 ∙ -8 = + 336 28 : 7 = + 4 f) Si a y b son dos números enteros de distinto signo, entonces: - El producto y el cuociente entre ellos es negativo. Ejemplo: 37 ∙ -5 = -185 125 : -5 = -25

Prioridad de operaciones Tanto en los números naturales como en los enteros, hay operaciones que tienen prioridad sobre otras. Existe un orden para resolver ejercicios como: -5 + 15 : 3 - 3 = ? ¿Qué se resuelve primero? El orden para ejecutar las operaciones que involucran paréntesis y operaciones combinadas es: 1° Paréntesis 2° Potencias 3° Multiplicación y/o división (de izquierda a derecha) 4° Adiciones y sustracciones

Consecutividad numérica • Sucesor Todo número entero tiene un sucesor, y se obtiene sumando 1 al número, es decir: Si n pertenece a ℤ, su sucesor será (n + 1). • Antecesor Todo número entero tiene un antecesor y se obtiene al restar 1 al número, es decir: Si n pertenece a ℤ, su antecesor será (n – 1). Enteros consecutivos (n – 1) antecesor n (n + 1) sucesor

Clasificación Paridad e imparidad • Números pares Números de la forma 2 n, con n perteneciente a ℤ. {. . , – 6, – 4, – 2, 0, 2, 4, 6, …} • Números impares Números de la forma 2 n+1, con n perteneciente a ℤ {. . , – 5, – 3, – 1, 1, 3, 5, …} Múltiplos Los múltiplos de un número entero son aquellos que se obtienen al multiplicarlo por algún otro número entero. Ejemplo: Múltiplos de 7: {…, ─14 , ─ 7, 0, 7, 14, 21, …} Múltiplos de 15: {…, ─ 45, ─ 30, ─ 15, 0, 15, 30, 45, …}

Clasificación Divisores Los divisores de un número entero son aquellos números enteros que lo dividen exactamente (división con resto cero). Ejemplo: Divisores de 6: {─ 6, ─ 3, ─ 2, ─ 1, 1, 2, 3, 6} Divisores de 24: {─ 24, ─ 12, ─ 8, ─ 6, ─ 4, ─ 3, ─ 2, ─ 1, 1, 2, 3, 4, 6, 8, 12, 24} Números primos Son aquellos números naturales que solo son divisibles por 1 y por sí mismos (solo tienen 2 divisores). {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …}.

Mínimo común múltiplo (m. c. m. ) El mínimo común múltiplo (m. c. m. ) de dos o más números naturales, corresponde al menor de los múltiplos positivos que tienen en común. El m. c. m. entre 2, 4 y 6 se puede obtener a través del siguiente método: Se divide cada número por números primos hasta que en cada columna quede 1. El producto de ellos corresponde al m. c. m. entre 2, 4 y 6. 2 4 6 2 1 2 3 2 1 3 3 1 m. c. m. = 2 ∙ 3 = 12

Máximo común divisor (M. C. D. ) El máximo común divisor de dos o más números naturales corresponde al mayor de los divisores positivos que tienen en común. El M. C. D. entre 36, 18 y 24 se puede obtener a través del siguiente método: Se divide por números primos que sean divisores comunes de los números, hasta que ya no se pueda dividir a todos en forma simultánea. El producto entre ellos corresponde al M. C. D. 36 18 24 2 18 9 6 3 12 3 4 M. C. D. = 2 ∙ 3 = 6

Valor absoluto El valor absoluto de un número representa la distancia del número al cero en la recta numérica. Por ejemplo, la distancia del 2 al origen es dos unidades, igual que la distancia del (– 2) al origen. La notación es: |2| = 2 y |– 2| = 2 0 -2 2 unidades Ejemplo: |– 13| = 13 |4| = 4 |– 17| = 17

Números Racionales (Q) Es el conjunto de todos aquellos números que se pueden escribir como fracción, es decir: Q= a b / a y b son enteros, y b es distinto de cero a: numerador denominador y b: Ejemplos: 2; 17; 0; -6; -45; -1; 14; -2; 0, 489; 2, 18; -0, 647 8 3 7

Amplificación y simplificación en Q • Amplificación Amplificar una fracción significa multiplicar, tanto el numerador como el denominador, por un mismo número. Ejemplo: Al amplificar la fracción 2 3 por 6 resulta: 2∙ 6 3∙ 6 = 12 18 • Simplificación Simplificar una fracción significa dividir, tanto el numerador como el denominador, por un mismo número. Las fracciones que no se pueden simplificar se llaman fracciones irreductibles. Ejemplo: Al simplificar la fracción 27 45 por 3 resulta: 27 : 3 45 : 3 = 9 15

Adición y sustracción en Q Existen distintas maneras ejemplificaremos: de 1. Si los denominadores son iguales: 4 15 + 7 15 = 11 15 y 4 15 – 7 15 = sumar y/o fracciones. Las 3. Si los denominadores son primos entre si: – 3 4 15 5 2. Si uno de los denominadores restar + 7 = 8 4∙ 8 + 5∙ 7 40 = 32 + 35 40 = 67 40 4. Aplicando mínimo común múltiplo (m. c. m. ): es múltiplo del otro: 2 15 + 7 45 = 2∙ 3 + 7∙ 1 45 = 6 +7 45 = 13 5 45 12 + 7 18 = 5∙ 3 + 7∙ 2 36 = 15 + 14 36 = 29 36

Multiplicación y división • Multiplicación Se multiplican numeradores y denominadores entre sí. Los productos pasan a ser el nuevo numerador y el nuevo denominador. Ejemplo: – 4 5 ∙ 7 8 = – 28 40 • División Se multiplica el dividendo por el inverso multiplicativo del divisor. Ejemplo: – 4 5 : 7 8 = – 4 5 ∙ 8 7 = – 32 35

Transformaciones Fracción a decimal Para transformar una fracción a número decimal se divide el numerador por el denominador hasta obtener resto 0. Ejemplo: Decimal finito a fracción Para transformar un número decimal finito a fracción, se debe contabilizar la cantidad de dígitos decimales, tal que el denominador de la fracción será una potencia de 10 con tantos ceros como dígitos decimales. Ejemplo: 3 dígitos decimales Potencia de 10 con 3 ceros

Transformaciones Decimal periódico a fracción Para transformar un número decimal periódico a fracción se escribe en el numerador todo el número sin la coma, menos la parte entera, y en el denominador un número formado por tantos nueves como cifras tenga el periodo. Ejemplo:

Transformaciones Decimal semiperiódico a fracción Para transformar un número decimal semiperiódico a fracción se escribe en el numerador todo el número sin la coma, menos la parte no periódica (incluyendo la parte entera y el anteperíodo), y en el denominador un número formado por tantos nueves como cifras tenga el periodo, seguido de tantos ceros como cifras tenga el anteperíodo. Ejemplo:

Conjunto de los números irracionales Los números irracionales son aquellos números que no se pueden escribir como fracción, ya que poseen infinitos decimales sin un patrón definido, no tienen período. Ejemplos:

Conjunto de los números irracionales Representación en la recta numérica Los números irracionales son números reales y por lo tanto, podemos ubicarlos en la recta numérica. ¿Cómo podríamos ubicar en la recta numérica ? Las raíces cuadradas exactas nos ayudan a determinar el resultado aproximado de las que son números irracionales. En este caso, Al menos, podremos decir que se encuentra entre 1 y 2. IR 0 1 2

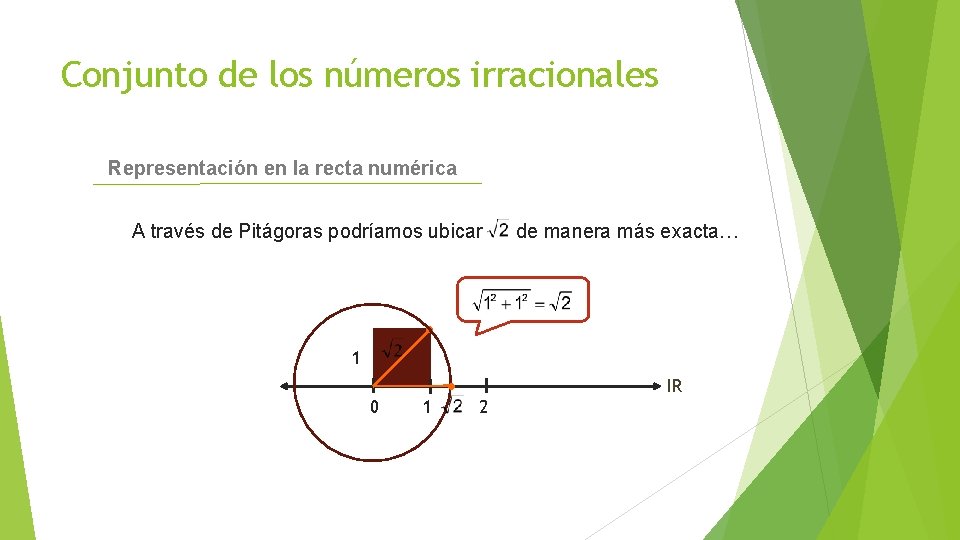
Conjunto de los números irracionales Representación en la recta numérica A través de Pitágoras podríamos ubicar de manera más exacta… 1 IR 0 1 2

Operatoria en Q* Operatoria entre un racional y un irracional Suma y resta: Al sumar y/o restar un irracional con un racional siempre resulta un número irracional. Ejemplo 1: es irracional, entonces también lo es. Si Ejemplo 2: La expresión es un irracional negativo. Se sabe que un número al cuadrado siempre es positivo, por lo que es negativo. Al aplicar el desarrollo de un cuadrado de binomio se tiene

Operatoria en Q* Operatoria entre un racional y un irracional Multiplicación y división: El producto y el cuociente entre un irracional y un racional siempre resulta un irracional (si el racional es distinto de cero). Ejemplos: es irracional.

Operatoria en Q* Suma y resta: La suma y resta entre irracionales NO siempre resulta un número irracional. Ejemplos: es irracional. es racional. Multiplicación y división: La multiplicación y división entre irracionales NO siempre resulta un irracional. Ejemplos: es racional. es irracional. es racional.

Ejemplo PSU 14. La suma de tres números impares consecutivos es siempre I) divisible por 3. II) divisible por 6. III) divisible por 9. Es (son) verdadera(s) A) B) C) D) E) solo I y III. solo II y III. I, II y III. ALTERNATIVA CORRECTA A Fuente : DEMRE - U. DE CHILE, Proceso de admisión 2010.

Ejemplo PSU 5. Se repartirá un premio de $ 624. 000 entre Ingrid, Gerardo y Jaime. Ingrid recibe del total, Gerardo recibe de lo quedará y Jaime el resto. ¿Cuánto reciben Gerardo y Jaime, respectivamente? A) $ 234. 000 y $ 260. 000 B) $ 156. 000 y $ 134. 000 C) $ 260. 000 y $ 364. 000 D) $ 260. 000 y $ 130. 000 E) $ 416. 000 y $ 208. 000 ALTERNATIVA CORRECTA D Fuente : DEMRE - U. DE CHILE, Modelo Proceso de admisión 2015.

Ejemplo PSU 10. En cada una de las rectas numéricas que se muestran en I), en II) y en III), el punto C es un punto tal que AC = I) II) A C C 0, 33 III) A C 0, 333 A) B) C) D) E) ? B 0, 4 0, 3 A . ¿En cuál(es) de ellas C = B ALTERNATIVA CORRECTA 0, 34 D B 0, 444 Solo en III. Solo en I y en II. En I, en II y en III. Fuente : DEMRE - U. DE CHILE, Proceso de admisión 2015.