Mtodos Analticos para Simulao Dinmica de Corpos Rgidos

Métodos Analíticos para Simulação Dinâmica de Corpos Rígidos Nãopenetrantes –Autor: David Baraff –Fonte: SIGGRAPH 1989 –Web: http: //www. pixar. com/companyinfo/research/deb/ César Candido Xavier - Aluno Mestrado CG 1

Objetivo u Apresentar de maneira sucinta Método Heurístico utilizado por David Baraff, para Simulação Dinâmica de Corpos Rígidos Nãopenetrantes. César Candido Xavier - Aluno Mestrado CG 2

Heurístico ? u Do grego heuristike: achado, descoberta; u Relacionado a heurística, ie, uma hipótese de trabalho adotada provisoriamente como idéia diretriz na pesquisa de fatos; u Método Heurístico: Técnicas (ex: autoeducação) que servem como ajuda na solução de um problema para o aprimoramento da performance. César Candido Xavier - Aluno Mestrado CG 3

Roteiro u Introdução u Motivação u Revisão alguns conceitos físicos u Simulação utilizando Métodos Analíticos u Modelando Contatos u Calculando Dinamicamente forças de contato corretamente u Solução Heurística u Restrições Adicionais u Conclusão César Candido Xavier - Aluno Mestrado CG 4

Introdução u Muitos trabalhos utilizam as leis dinâmica Newtoniana para simular sistemas de corpos rígidos (CR); u Toda simulação realística de corpos rígidos exige que não haja inter-penetração de dois quaisquer corpos; u Foco do “Paper”: Dado um número de corpos rígidos poliédricos, calcular as forças que naturalmente surgem para prevenir a interpenetração. César Candido Xavier - Aluno Mestrado CG 5

Motivação Moore e Hahn fizeram os primeiros trabalhos (1988) utilizando métodos analíticos p/ cálculo de forças (impulso) entre CR; u O método utilizado p/ corpos em repouso, entretanto, era não analítico. Modelo Utilizado p/ corpos em repouso: série de colisões ocorrendo freqüentemente. Modelo Analítico de forças que não é válido; u Platt e Barr utilizaram “Penalty Forces”; e u Moore e Wilhelms utilizaram forças elásticas. u César Candido Xavier - Aluno Mestrado CG 6

Motivação (continuação) Métodos Errôneos Vantagens: u - fácil de implementar; pouco complexidade; e extensível p/ corpos não rígidos. Desvantagens: u - as simulações apresentam resultados aproximados; a correção da simulação é difícil de se verificar em alguns casos; e requer ajustes para condições diferentes na simulação. César Candido Xavier - Aluno Mestrado CG 7

Motivação (continuação) Métodos Analíticos u Vantagens: - dão respostas exatas; - produzem E. D. O. que requerem bem menos passos no tempo durante simulação; e - a correção da simulação é fácil de se verificar (baseadas diretamente da dinâmica Newtoniana). u Desvantagens: -são muito mais complexos de derivar e implementar. César Candido Xavier - Aluno Mestrado CG 8

Revisão u Centro de Massa: u Momento Linear: u Força: u Torque: u Momento Angular: u Momento de Inércia: César Candido Xavier - Aluno Mestrado CG 9

Simulação via Métodos Analíticos u Tratamento diferenciado entre forças de colisão e forças de contato em repouso. u Forças de colisão: - forças descontínuas (impulsivas); - dimensão m v; e - causam descontinuidades na velocidade do CR. u Forças de contato: - são contínuas em algum intervalo não-nulo; - dimensão m a; e - não causam descontinuidades na velocidade do CR. César Candido Xavier - Aluno Mestrado CG 10

u u Simulador interage na solução de um par de EDO acopladas, via uso do método numérico de Runge-Kutta de 4º Ordem ou Adams-Moulton; Ao integrador é passado todas condições iniciais dos corpos; Métodos Analíticos introduzem descontinuidades nas velocidades dos corpos quando há colisão. Não teremos boa solução se integrarmos sobre estes intervalos. . . Solução: – Devemos descobrir o tempo no qual uma colisão ocorrerá!!! u Foi utilizado o método descrito por Moore e Wilhelms. César Candido Xavier - Aluno Mestrado CG 11

u Resolvendo uma Colisão: - uma vez determinado o tempo da colisão, o integrador é parado; - faz-se o cálculo das novas forças; - calcula-se as novas velocidades dos corpos em colisão (novas condições iniciais); e - reinicializa-se o integrador. César Candido Xavier - Aluno Mestrado CG 12

Modelando Contatos u Contato: colidindo ou em repouso; u Dois corpos A e B se tocam em um número finito de contatos (pontos de contato); u pa(to): posição de um ponto de contato de um CR A no instante t 0; u Sejam dois pontos ‘a’ e ‘b’ dos CR A e B que estão em contato: pa (t 0)=p=pb (t 0) César Candido Xavier - Aluno Mestrado CG 13

Características pa(to) e pb(to) : u - Variáveis no tempo; - Variam de acordo com os independentemente dos CR respectivamente; e i. iii. movimentos A e B indica: colisão; repouso; ou separando-se, César Candido Xavier - Aluno Mestrado CG 14

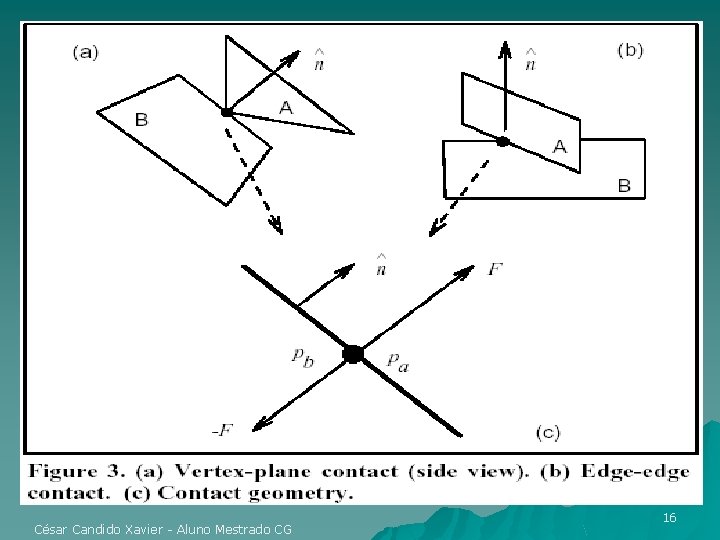
u Associado a cada ponto de contato: – Força (possivelmente nula); e – Um vetor unitário normal a superfície. u Contatos tipo Vértice-Plano – Corpo A: vértice; e – Corpo B: plano com normal u em p. b Contatos tipo Aresta-Aresta – Um corpo é definido como Corpo A arbitrariamente. – N é mutuamente perpendicular as arestas em contato e direcionado se afastando de B. Obs. : na ausência de atrito é colinear com César Candido Xavier - Aluno Mestrado CG . 15

César Candido Xavier - Aluno Mestrado CG 16

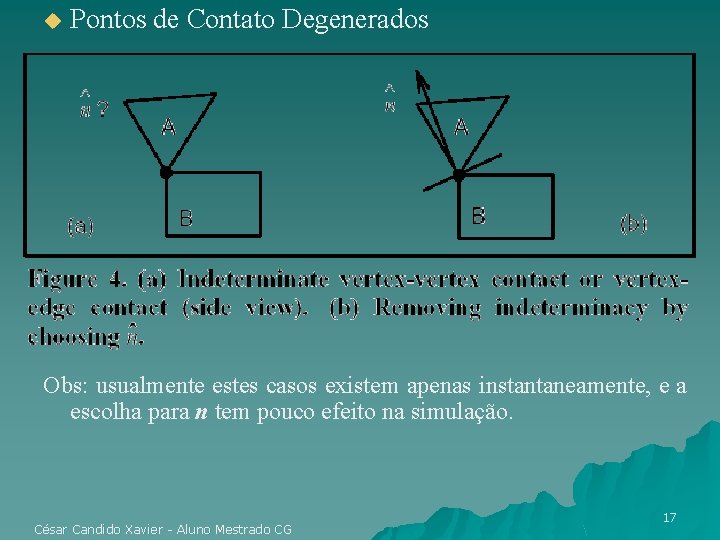
u Pontos de Contato Degenerados Obs: usualmente estes casos existem apenas instantaneamente, e a escolha para n tem pouco efeito na simulação. César Candido Xavier - Aluno Mestrado CG 17

Pontos de Contato Degenerados u u Cálculo da intensidade nestes casos é um problema NP-completo (teorema de Palmer); Solução: extensão de um plano local em B, e dá-se o tratamento de contatos tipo Vértice-Plano. Restrição dos Pontos de Contato – – – Pontos extremos; Vértices do segmento de reta; e Polígono de contato das regiões. César Candido Xavier - Aluno Mestrado CG 18

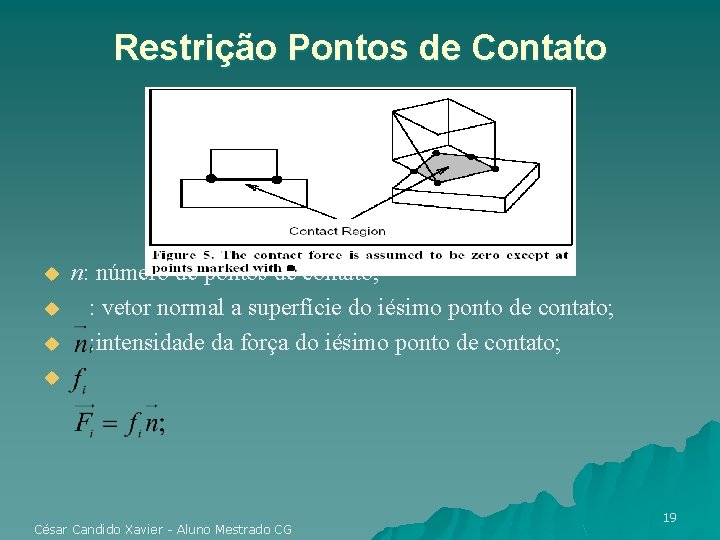
Restrição Pontos de Contato u u u n: número de pontos de contato; : vetor normal a superfície do iésimo ponto de contato; : intensidade da força do iésimo ponto de contato; u César Candido Xavier - Aluno Mestrado CG 19

Calculando dinamicamente forças de contato corretamente u Um vetor é uma força de contato de magnitude correta se: 1. 2. 3. 4. não permite que os corpos interpenetrem-se; a força de contato “empurra” mas não “puxa”; forças de contato ocorrem apenas nos pontos de contato; e visto como uma função do tempo, as forças de contato são contínuas. César Candido Xavier - Aluno Mestrado CG 20

Restrições p/ Não-Penetrações u u É suficiente examinar o movimento relativo dos corpos em cada ponto de contato; Seja a função característica: César Candido Xavier - Aluno Mestrado CG 21

u Quem seriam e ? Seja to o instante no qual há o choque entre os CR A e B estão colidindo (nunca acontecerá) - A e B estão se separando (fi=0) César Candido Xavier - Aluno Mestrado CG 22

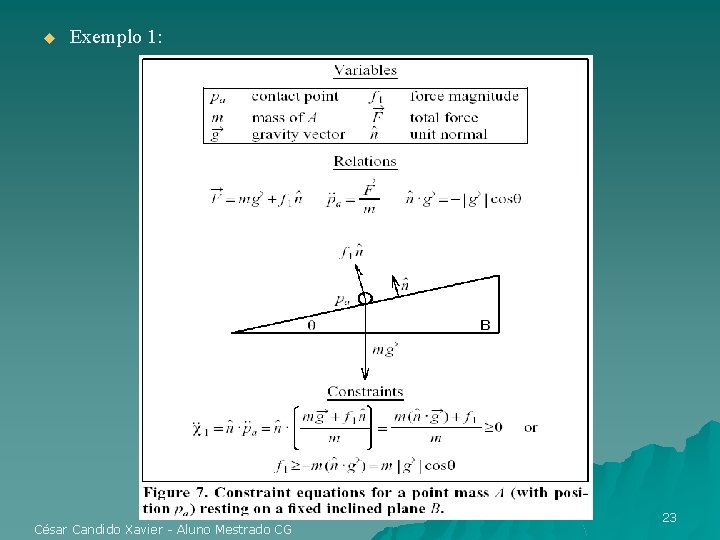
u Exemplo 1: César Candido Xavier - Aluno Mestrado CG 23

u Exemplo 2: César Candido Xavier - Aluno Mestrado CG 24

u , para 1≤ i ≤ n Matriz formulação das condições (1) e (2) (não há inter-penetração); u fi ≥ 0, para 1≤ i ≤ n (forcas somente “empurram”); César Candido Xavier - Aluno Mestrado CG 25

u Podemos escrever a representação matricial, portanto, da seguinte forma: – – – César Candido Xavier - Aluno Mestrado CG 26

Programação Linear (PL) u u u Encontrar um vetor que satisfaz: Mx ≥ c (M é matriz e c é um vetor) que minimiza uma função linear z(x) é um exemplo de um problema típico de PL; Se existem x que satisfazem todas as restrições dizemos que o sistema é realizável e cada x é uma solução realizável; Se x é uma solução realizável que minimiza z, são ditos sistemas limitados e x uma solução ótima. PL é um problema polinomial no tempo; Se, entretanto, é explorado o fato de A ser tipicamente uma matriz esparsa, a solução é O(n); César Candido Xavier - Aluno Mestrado CG 27

Formulação das condições (3) e (4) u Uma f que atenda a correta!!! e , não será necessariamente – Exemplo 1: f=mgcos(θ) é a única solução correta, porém f=2 mgcos(θ) é solução realizável que previne a inter-penetração, porém acelera incorretamente, afastando o CR A de B. César Candido Xavier - Aluno Mestrado CG 28

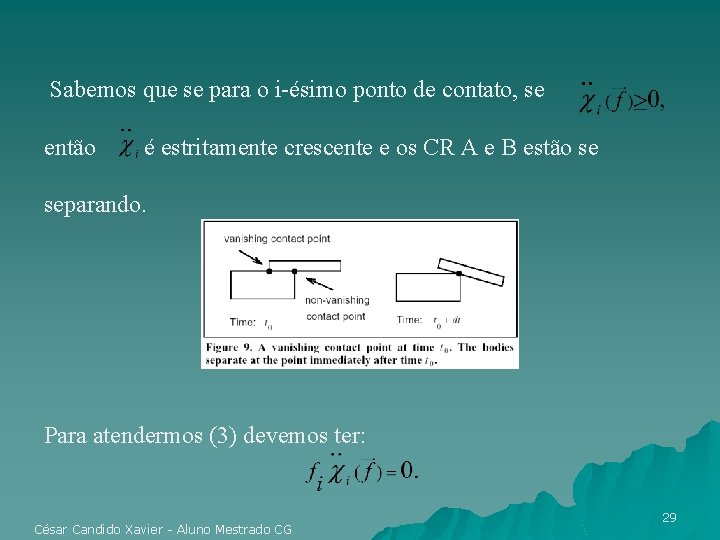
Sabemos que se para o i-ésimo ponto de contato, se então é estritamente crescente e os CR A e B estão se separando. Para atendermos (3) devemos ter: César Candido Xavier - Aluno Mestrado CG 29

Para 1≤ i ≤ n, nossas restrições passam a ser escritas como: Ou: César Candido Xavier - Aluno Mestrado CG 30

O termo que envolve a forma é quadrático em fi; u Programação Quadrática, diferentemente de PL é um problema NP-difícil de um modo geral; u Modelando contatos sem atrito A é positivamente semidefinida (PSD), e programas quadráticos podem teoricamente ser resolvidos em tempo polinomial (não existe tal algoritmo. . . ) u Não há porque acreditar que com atrito A continuará sendo PSD. . . u u SOLUÇÃO: desenvolvimento heurístico para este problema. . . César Candido Xavier - Aluno Mestrado CG de um algoritmo 31

Solução Heurística Uma determinada configuração de corpos tem apenas uma configuração de movimentos corretos. Seja V e C os conjuntos de pontos que estão deixando de existir e não estão deixando de existir, ou seja: V={j | ponto de contato que está sumindo} C={k | ponto de contato que não está sumindo} César Candido Xavier - Aluno Mestrado CG 32

Sabemos que para qualquer solução correta : – – Podemos escrever: César Candido Xavier - Aluno Mestrado CG 33

Exemplo: Seja um sistema quadrático com restrições em quatro pontos de contato, com V={1, 3} e C={2, 4} César Candido Xavier - Aluno Mestrado CG 34

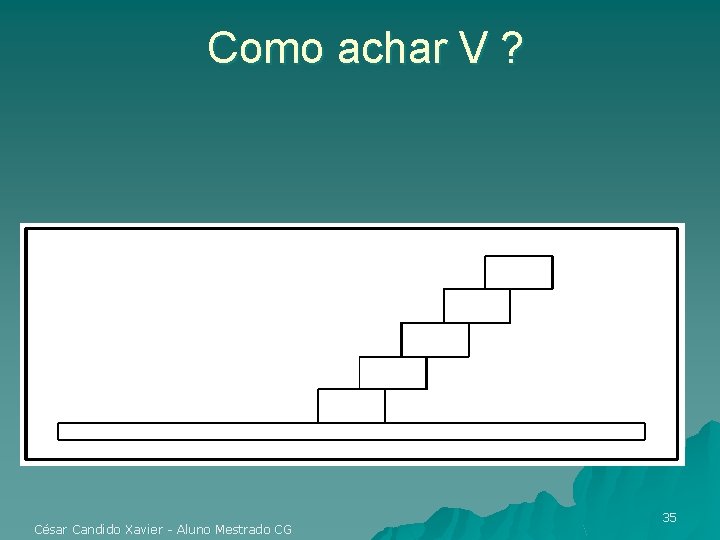
Como achar V ? César Candido Xavier - Aluno Mestrado CG 35

1) Solução mais simples: V=Ø Não existem pontos de contato que estão deixando de existir, e f está sujeito às seguintes restrições: Através de diversas simulações constatou-se que a solução V=Ø é correta para a grande maioria dos casos. César Candido Xavier - Aluno Mestrado CG 36

2) Predizendo um conjunto não-vazio de V Se for encontrado uma configuração com pontos de contatos que estão deixando de existir, a adivinhação de que V=Ø resultará em um sistema indeterminado. Solução: encontrar uma solução aproximada fa que satisfaça às restrições: Seja o vetor residual: César Candido Xavier - Aluno Mestrado CG 37

Se fa for uma solução correta, para todos pontos j, que estão deixando de existir, , e para todos os outros pontos k, . 2. 1) Encontrando fa Aproximadas A heurística utilizada para encontrar a solução aproximada é: escolha fa que minimiza a seguinte função: , sujeita às seguintes restrições: César Candido Xavier - Aluno Mestrado CG 38

2. 2) Tratando com Predições Incorretas -Tendo n pontos de contatos, deveríamos testar todas as 2 n possibilidades ? - A implementação desenvolvida leva em consideração que pontos deixando de existir ocorrem com pouquíssima freqüência. . . - Energia é adicionada ao sistema, produzindo resultados incorretos. . . César Candido Xavier - Aluno Mestrado CG 39

-. . . porém o (d)efeito é mascarado pelo fato de que estas configurações são singulares, ou seja é aplicado apenas por um período pequeno no tempo. - Descobriu-se que, no pequeno intervalo de tempo na qual é aplicado, levando-se em conta que é usualmente uma boa aproximação da solução correta produziu resultados satisfatórios. César Candido Xavier - Aluno Mestrado CG 40

Restrições Adicionais Restrições Holonômicas (figuras articuladas) podem ser adicionadas de uma maneira consistente; u Barzel e Barr mantiveram restrições holonômicas pela introdução de forças de restrição que satisfaziam ao sistema linear u u Todo o sistema é resolvido conforme descrito anteriormente , à exceção do somatório mínimo das forças, o qual levará em consideração tão somente as restrições não holonômicas das forças. César Candido Xavier - Aluno Mestrado CG 41

uÉ consistente com a formulação proposta, uma vez que programação linear permite restrições com igualdades; u Não estão sujeitos as condições (2); u Todo o sistema é resolvido conforme metodologia apresentada, à exceção do somatório mínimo de forças, o qual levará em questão apenas as forças de restrições não-holonômicas; e u Utilizado pacote de PL esparsa p/ resolver em O(n). César Candido Xavier - Aluno Mestrado CG 42

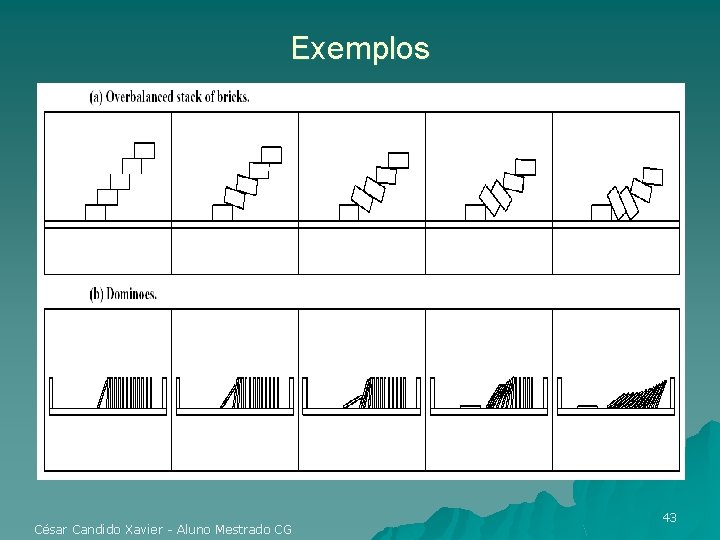
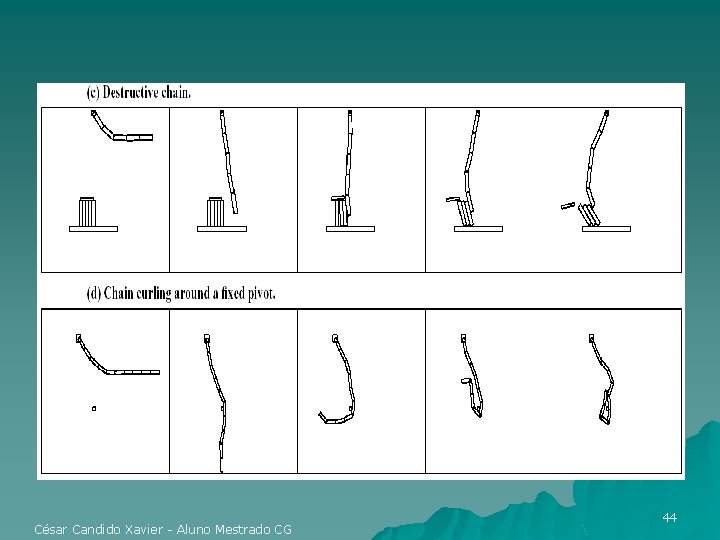
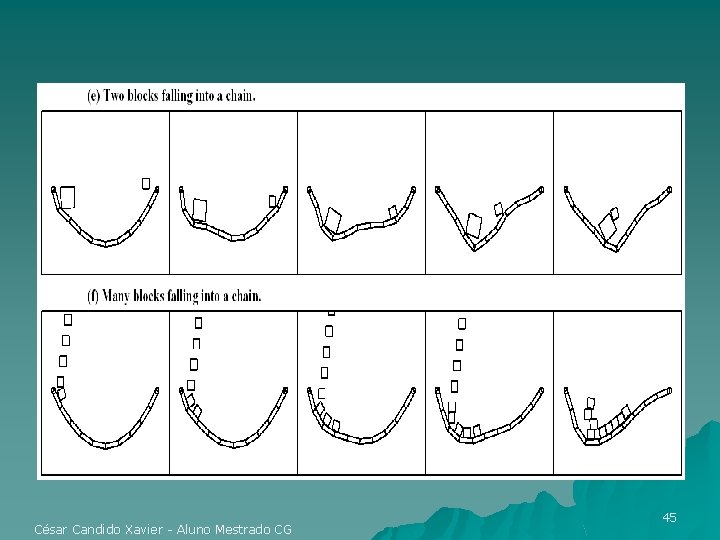
Exemplos César Candido Xavier - Aluno Mestrado CG 43

César Candido Xavier - Aluno Mestrado CG 44

César Candido Xavier - Aluno Mestrado CG 45

Conclusão u u A solução proposta para encontrar as forças de contato entre corpos poliédricos, foi baseada em uma heurística, cuja solução é encontrada via uso de técnicas de Programação Linear; A solução proposta permite trabalhar com restrições holonômicas; O grande esforço computacional do algoritmo é voltado na solução de um sistema linear de desigualdades; e O algoritmo heurístico utilizado ocasionalmente falhará e uma solução aproximada é utilizada. Isto adiciona energia a simulação mas não resulta em nenhum efeito visual insatisfatório. César Candido Xavier - Aluno Mestrado CG 46