Modellizzare le decisioni razionali con la teoria dei

Modellizzare le decisioni razionali con la teoria dei giochi. Gian Italo Bischi DESP - Dipartimento di Economia, Società e Politica Università di Urbino “Carlo Bo” gian. bischi@uniurb. it http: //www. mdef. it/gian-italo-bischi/ Caldè 27 Luglio 2013

Galileo, da “ Il Saggiatore” Galileo Galilei 1564 -1642 La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi agli occhi (io dico l’Universo), ma non si può intendere se prima non si impara a intender la lingua, e conoscer i caratteri, ne’ quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi ed altre figure geometriche, senza i quali mezi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro laberinto.

The unreasonable effectiveness of mathematics in the natural sciences (Eugene P. Wigner, Nobel per la Fisica nel 1963) Capacità di descrivere e prevedere i fenomeni naturali: una mela, un pianeta, una particella elementare, un fluido, un gas … Una sfida: Può la matematica aiutare anche a descrivere, prevedere i comportamenti umani? (Hari Seldon, Parker Pyne …). Ma il problema del bar di Santa Fe. . .

Vito Volterra (1860 -1940) Il matematico si trova in possesso di uno strumento mirabile e prezioso, creato dagli sforzi accumulati per lungo andare di secoli dagli ingegni più acuti e dalle menti più sublimi che siano mai vissute. Egli ha, per così dire, la chiave che può aprire il varco a molti oscuri misteri dell’universo, ed un mezzo per riassumere in pochi simboli una sintesi che abbraccia e collega vasti e disparati risultati di scienze diverse Vito Volterra (1860 -1940) […] Ma è intorno a quelle scienze nelle quali le matematiche solo da poco tempo hanno tentato d’introdursi, le scienze biologiche e sociali, che è più intensa la curiosità, giacché è forte il desiderio di assicurarsi se i metodi classici, i quali hanno dato così grandi risultati nelle scienze meccanico-fisiche, sono suscettibili di essere trasportati con pari successo nei nuovi ed inesplorati campi che si dischiudono loro dinanzi. dal discorso inaugurale per l’anno accademico 1901 -1902 dell’Università di Roma

Problema del monopolista: Più produco e più guadagno? q = quantità prodotta p = prezzo unitario di vendita c = costo unitario di produzione Profitto = Ricavo – Costo = p q – c q = (p – c) q Teorema. Se p > c allora il profitto cresce ogniqualvolta cresce la produzione Ma ci sono sempre dei consumatori disposti a comprare ciò che si produce al prezzo imposto dal monopolista ?

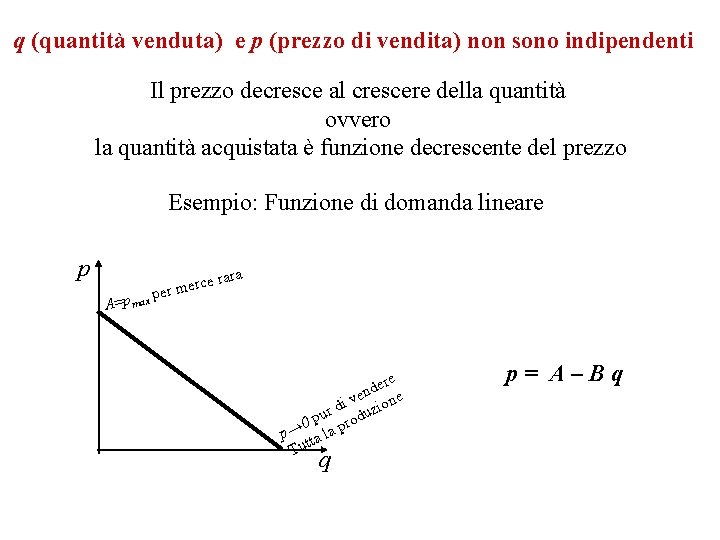
q (quantità venduta) e p (prezzo di vendita) non sono indipendenti Il prezzo decresce al crescere della quantità ovvero la quantità acquistata è funzione decrescente del prezzo Esempio: Funzione di domanda lineare p e rara r merc e p x A=p ma ere d n i ve zione d r pu rodu 0 p→ ta la p t Tu q p= A–Bq

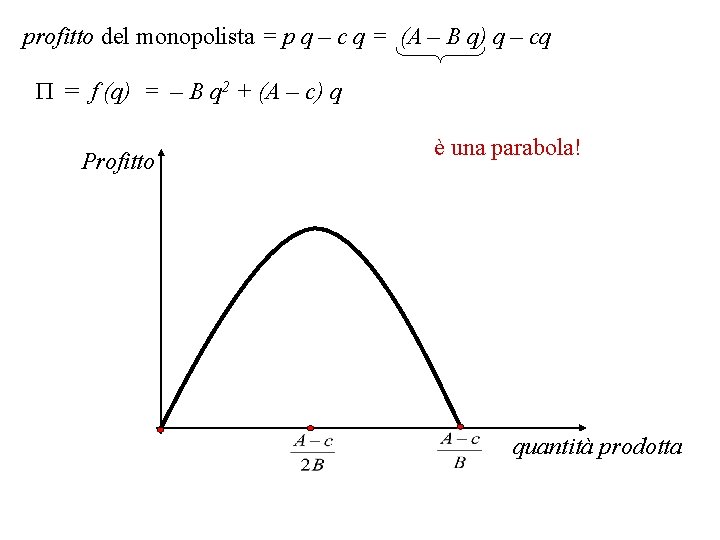
profitto del monopolista = p q – c q = (A – B q) q – cq P = f (q) = – B q 2 + (A – c) q Profitto è una parabola! quantità prodotta

Problema del duopolio A. Cournot, Récherches sur les principes matématiques de la théorie de la richesse, 1838. Due produttori, 1 e 2, vendono lo stesso prodotto Il produttore 1 produce e immette nel mercato q 1 con costi c 1 q 1 Il produttore 2 produce e immette nel mercato q 2 con costi c 2 q 2 prezzo: p = A – B QTOT = A – B ( q 1 + q 2) Profitto produttore 1: P 1 = pq 1 – c 1 q 1 = [ A – B ( q 1 + q 2 )]q 1 – c 1 q 1 Profitto produttore 2: P 2 = pq 2 – c 2 q 2 = [ A – B ( q 1 + q 2 )]q 2 – c 2 q 2

P 1 = [ A – B ( q 1 + q 2)]q 1 – c 1 q 1 = – Bq 12 + (A – c 1 –Bq 2 )q 1 Max per P 2 = [ A – B ( q 1 + q 2)]q 2 – c 2 q 2 = – Bq 22 + (A – c 2 Bq 1 )q 2 Max per q 2 = Equilibrio: q 2 ) (q 1 r 2 Equilibrio di Cournot-Nash q 1 = r 1 (q 2) q 1

Non basta semplicemente adattare i metodi e i ragionamenti della fisica alla modellizzazione dell’economia perché l’economia è una scienza morale. Essa ha a che vedere con motivazioni, aspettative, incertezze psicologiche. È come se la caduta della mela al suolo dipendesse dalle aspirazioni della mela, se per lei sia conveniente o meno cadere a terra, se il suolo vuole che essa cada, e se vi sono stati errori di calcolo da parte della mela sulla sua reale distanza dal centro del John Maynard Keynes (1883– 1946) pianeta” Aggiungiamo: come e quanto la mela si fa condizionare dal comportamento delle altre mele dello stesso albero o di alberi vicini, le aspirazioni e aspettative dellac mela, le informazioni che la mela ha, ecc.

Verso una “Matematica per le decisioni”. Occorre introdurre una descrizione formale di azioni possibili, informazioni sugli esiti, preferenze, razionalità. Parte oggettiva: A= insieme di azioni {a 1, a 2, …, am} E = insieme di eventi {e 1, e 2, …, em} con ei= h(ai), i=1, …m Parte soggettiva: L’insieme E sia dotato di una relazione di preferenza: simbolo … ei ; -)) ej significa: ei preferito o indifferente a ej, ovvero ej non peggio di ei Preferenze razionali: transitività arancia ; -)) pera e pera ; -)) mela, allora arancia ; -)) mela

Perché individui non transitivi non ci sono? Una possibile spiegazione evolutiva (money pump) E = {x 1=mela, x 2=pera, x 3=arancia} Supponiamo che un individuo abbia preferenze non transitive (o cicliche) Preferenze x 1 ; -) x 2 , x 2 ; -) x 3 , x 3 ; -) x 1 Gli regalo una mela. Poi gli offro in cambio un’arancia e gli chiedo 1 cent in aggiunta. Poi gli offro una pera e gli chiedo 1 cent in aggiunta. Poi gli offro una mela e gli chiedo 1 cent in aggiunta. Poi…

Un esempio: da transitività individuale a non transitività collettiva Il paradosso di Condorcet 1° 2° 3° 1 A B C 2 B C A 3 C A B Cioè per l’elettore 1 A ; -) B ; -) C ecc. Con un unico turno non c’è vincitore Due turni: I) A contro B …. vince A II) A contro C …. vince C Quindi per la collettività dei 3 elettori A ; -) B e C; -) A Proviamo a cambiare il primo turno I) B contro C …. vince B II) B contro A … vince A (come sapevamo) Quindi: B ; -) C e A ; -) B Riassumendo: A ; -) B , B ; -) C , C ; -) A preferenze cicliche!!

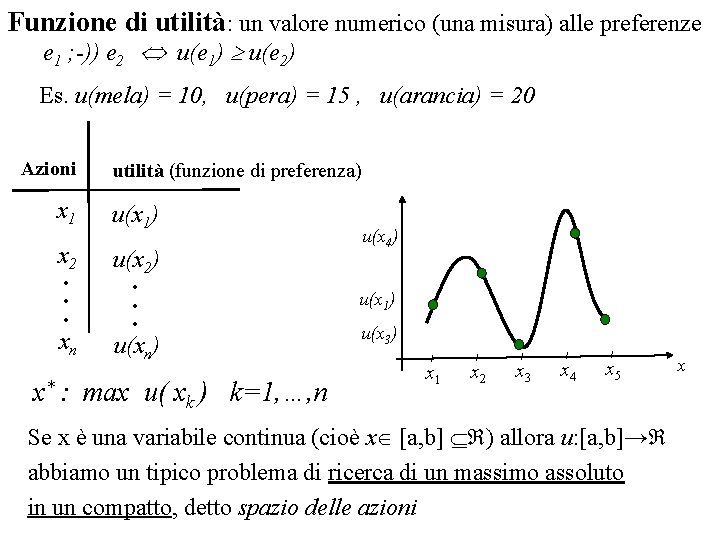
Funzione di utilità: un valore numerico (una misura) alle preferenze e 1 ; -)) e 2 u(e 1) u(e 2) Es. u(mela) = 10, u(pera) = 15 , u(arancia) = 20 Azioni utilità (funzione di preferenza) x 1 u(x 1) x 2 u(x 2) . . . xn . . . u(xn) x* : max u( xk ) k=1, …, n u(x 4) u(x 1) u(x 3) x 1 x 2 x 3 x 4 x 5 Se x è una variabile continua (cioè x [a, b] ) allora u: [a, b]→ abbiamo un tipico problema di ricerca di un massimo assoluto in un compatto, detto spazio delle azioni x

Interazione strategica John (János) von Neumann Budapest (Ungheria) 1903 Washington (USA) 1957 Princeton, 1947 Oskar Morgenstern Görlitz (Germania) 1902 Princeton (USA) 1977

DECISIONI IN PRESENZA DI INTERAZIONE STRATEGICA Dall'oroscopo di Linda Wolf del 3 dicembre 2009 Ariete. Anche se siete sicuri del fatto vostro fate molta attenzione alle decisioni degli altri

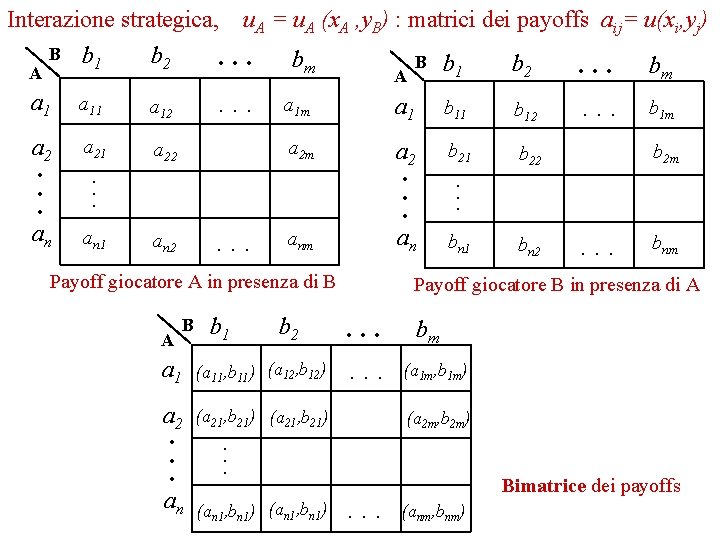
Interazione strategica, u. A = u. A (x. A , y. B) : matrici dei payoffs aij= u(xi, yj) B b 1 b 2. . . bm B b b. . . b A A a 11 a 12 a 21 a 22 an an 1 . . . an 2 A b 1 a 1 b 12 a 2 m a 2 b 21 b 22 an bn 1 bn 2 . . . anm b 2 a 1 (a 11, b 11) (a 12, b 12) a 2 (a 21, b 21) . . . an 2 a 1 m Payoff giocatore A in presenza di B B 1 . . . b 1 m b 2 m . . . bnm Payoff giocatore B in presenza di A . . . bm (a 1 m, b 1 m) (a 2 m, b 2 m) . . . (an 1, bn 1) . . . m . . . Bimatrice dei payoffs (anm, bnm)

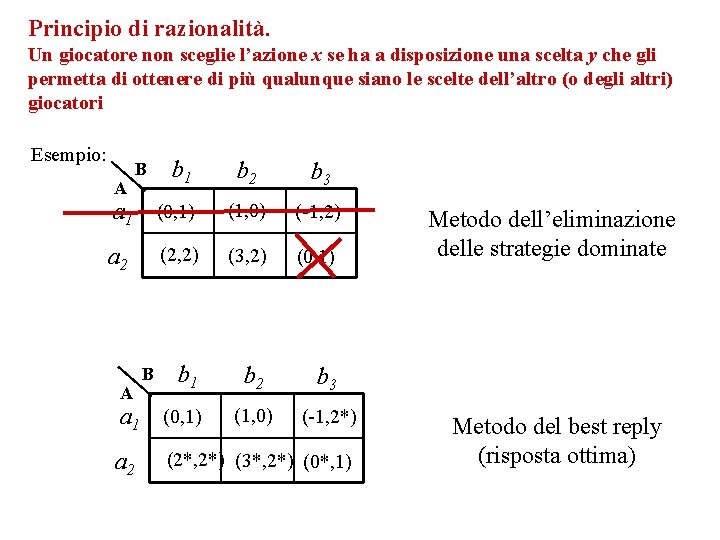
Principio di razionalità. Un giocatore non sceglie l’azione x se ha a disposizione una scelta y che gli permetta di ottenere di più qualunque siano le scelte dell’altro (o degli altri) giocatori Esempio: b 1 b 2 b 3 a 1 (0, 1) (1, 0) (-1, 2) a 2 (2, 2) (3, 2) (0, 1) b 1 b 2 b 3 (1, 0) (-1, 2*) A A B B a 1 (0, 1) a 2 (2*, 2*) (3*, 2*) (0*, 1) Metodo dell’eliminazione delle strategie dominate Metodo del best reply (risposta ottima)

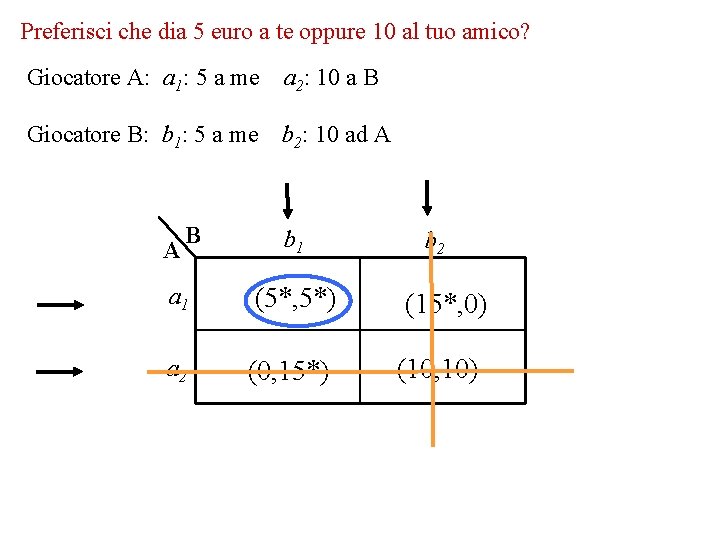
Preferisci che dia 5 euro a te oppure 10 al tuo amico? Giocatore A: a 1: 5 a me a 2: 10 a B Giocatore B: b 1: 5 a me b 2: 10 ad A A B b 1 a 1 (5*, 5*) a 2 (0, 15*) b 2 (15*, 0) (10, 10)

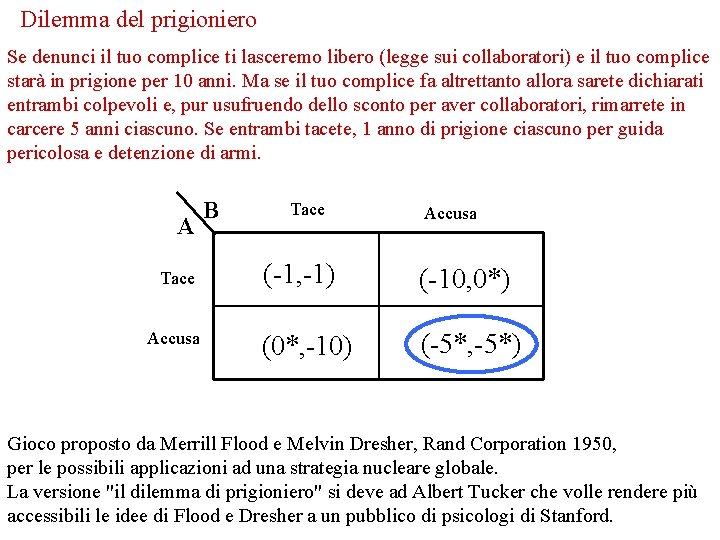
Dilemma del prigioniero Se denunci il tuo complice ti lasceremo libero (legge sui collaboratori) e il tuo complice starà in prigione per 10 anni. Ma se il tuo complice fa altrettanto allora sarete dichiarati entrambi colpevoli e, pur usufruendo dello sconto per aver collaboratori, rimarrete in carcere 5 anni ciascuno. Se entrambi tacete, 1 anno di prigione ciascuno per guida pericolosa e detenzione di armi. A Tace Accusa B Tace Accusa (-1, -1) (-10, 0*) (0*, -10) (-5*, -5*) Gioco proposto da Merrill Flood e Melvin Dresher, Rand Corporation 1950, per le possibili applicazioni ad una strategia nucleare globale. La versione "il dilemma di prigioniero" si deve ad Albert Tucker che volle rendere più accessibili le idee di Flood e Dresher a un pubblico di psicologi di Stanford.

Dilemma del Pescatore Fisherman C R Moderate Intensive exploitaton exploitation (cooperative) (competitive) Moderate exploitaton (cooperative) (3, 3) Intensive exploitation (competitive) (4, 1) (1, 4) E la mano invisibile di Adam Smith? (2, 2) Un tipico dilemma sociale Hardin, G. “The tragedy of the commons”, Science (1968).

In generale … b 1 b 2 a 1 (a, a) (b, c) a 2 (c, b) (d, d) A B con c > a > d > b Altre situazioni : ü Scambio a scatola chiusa ü Corsa agli armamenti e politiche di disarmo ü Parlare a voce alta in pizzeria üInquinare o no? üPorto il casco per correre in bici?

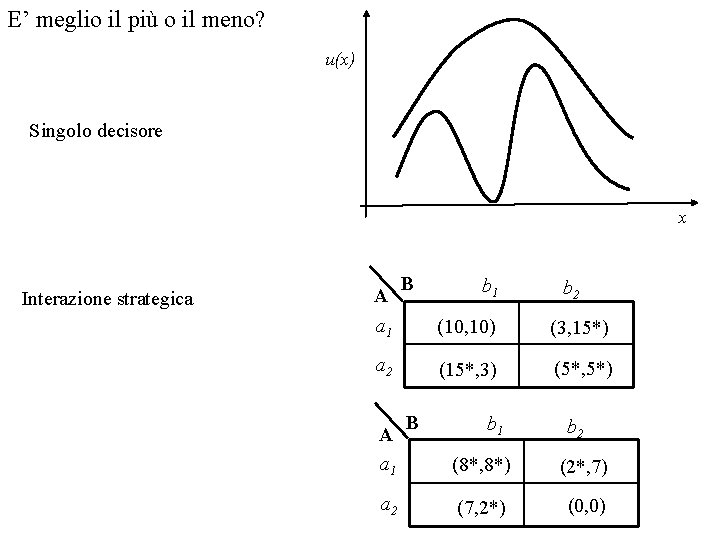
E’ meglio il più o il meno? u(x) Singolo decisore x Interazione strategica A a 1 B a 2 A a 1 a 2 B b 1 b 2 (10, 10) (3, 15*) (15*, 3) (5*, 5*) b 1 b 2 (8*, 8*) (2*, 7) (7, 2*) (0, 0)

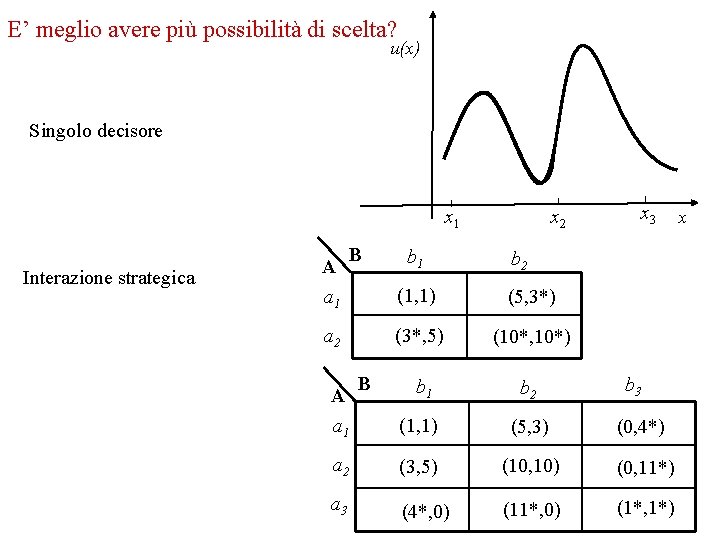
E’ meglio avere più possibilità di scelta? u(x) Singolo decisore x 2 x 1 Interazione strategica A a 1 B b 1 x 3 b 2 (1, 1) (5, 3*) (3*, 5) (10*, 10*) b 1 b 2 (1, 1) (5, 3) (0, 4*) a 2 (3, 5) (10, 10) (0, 11*) a 3 (4*, 0) (11*, 0) (1*, 1*) a 2 A a 1 B b 3 x

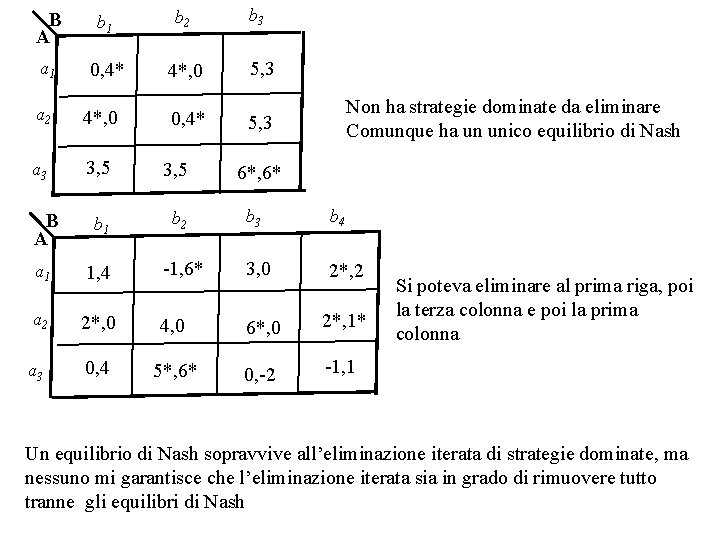
B A b 1 b 2 a 1 0, 4* 4*, 0 b 3 5, 3 Non ha strategie dominate da eliminare Comunque ha un unico equilibrio di Nash a 2 4*, 0 a 3 3, 5 B A b 1 b 2 b 3 b 4 a 1 1, 4 -1, 6* 3, 0 2*, 2 a 2 2*, 0 4, 0 6*, 0 2*, 1* a 3 0, 4 5*, 6* 0, -2 -1, 1 0, 4* 5, 3 6*, 6* Si poteva eliminare al prima riga, poi la terza colonna e poi la prima colonna Un equilibrio di Nash sopravvive all’eliminazione iterata di strategie dominate, ma nessuno mi garantisce che l’eliminazione iterata sia in grado di rimuovere tutto tranne gli equilibri di Nash

B b 1 b 2 a 1 (1, 1) (0, 0) a 2 (0, 0) A B b 1 b 2 a 1 (1, 1) (0, 0) a 2 (0, 0) (1, 1) A tenere la destra o la sinistra? B b 1 b 2 a 1 (1, 2) (0, 0) a 2 (0, 0) (2, 1) A battaglia dei sessi: shopping o partita? Facile se ciascuno conosce la matrice dei payoff e sa che l’altro è razionale e sa che l’altro sa… Gioco di puro coordinamento. Se giochiamo la stressa strategia va bene per entrambi, se giochiamo diverso male per entrambi. Occorre comunicazione preliminare, (poi non c’è pericolo di defezione) Anche qui due equilibri di Nash, ma difficile accordo preliminare. Se ciascuno persegue il proprio Nash preferito si finisce in (0, 0). E anche un eccesso di altruismo da parte di entrambi…

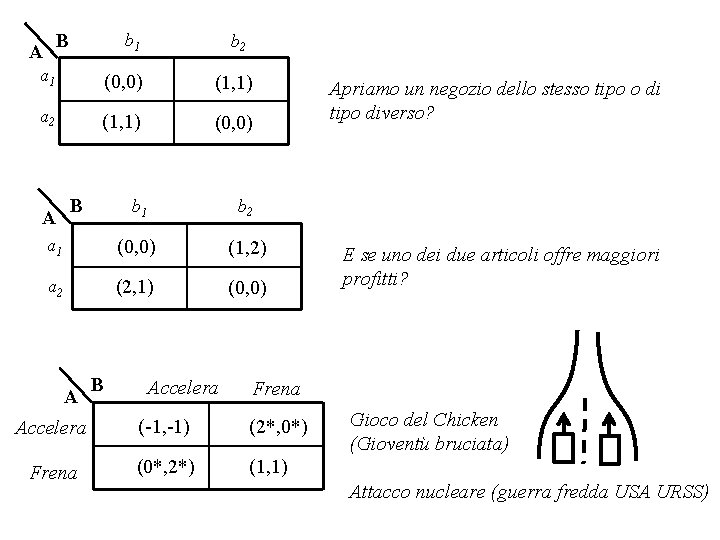
B A b 1 b 2 a 1 (0, 0) (1, 1) a 2 (1, 1) (0, 0) B b 1 b 2 a 1 (0, 0) (1, 2) a 2 (2, 1) (0, 0) A A B Accelera Apriamo un negozio dello stesso tipo o di tipo diverso? E se uno dei due articoli offre maggiori profitti? Frena Accelera (-1, -1) (2*, 0*) Frena (0*, 2*) (1, 1) Gioco del Chicken (Gioventù bruciata) Attacco nucleare (guerra fredda USA URSS)

Giochi a somma zero non ci sono equilibri di Nash inefficienti b 1 b 2 b 3 B A minimo guadagno su ogni riga a 1 9 , -9 3 , -3 0 , 0 0 a 2 6, -6 5 , -5 7, -7 5 a 3 -1 , 1 4, -4 9 , -9 -1 9 5 9 max fra i min guadagni (maxmin) massima perdita su ogni colonna min fra le max perdite (minmax) Equilibrio: maxmin = minmax = sella della matrice

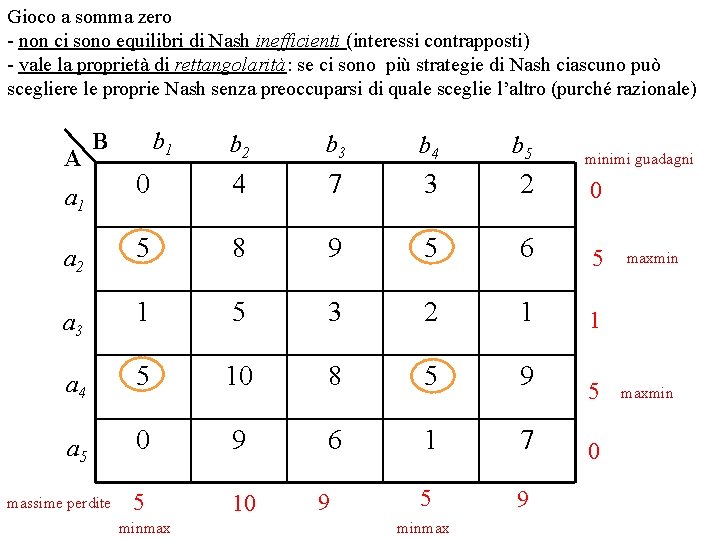
Gioco a somma zero - non ci sono equilibri di Nash inefficienti (interessi contrapposti) - vale la proprietà di rettangolarità: se ci sono più strategie di Nash ciascuno può scegliere le proprie Nash senza preoccuparsi di quale sceglie l’altro (purché razionale) b 1 B b 2 b 3 b 4 b 5 0 4 7 3 2 0 5 8 9 5 6 5 1 5 3 2 1 1 a 4 5 10 8 5 9 a 5 0 9 6 1 7 5 10 5 9 A a 1 a 2 a 3 massime perdite minmax 9 minmax minimi guadagni 5 0 maxmin

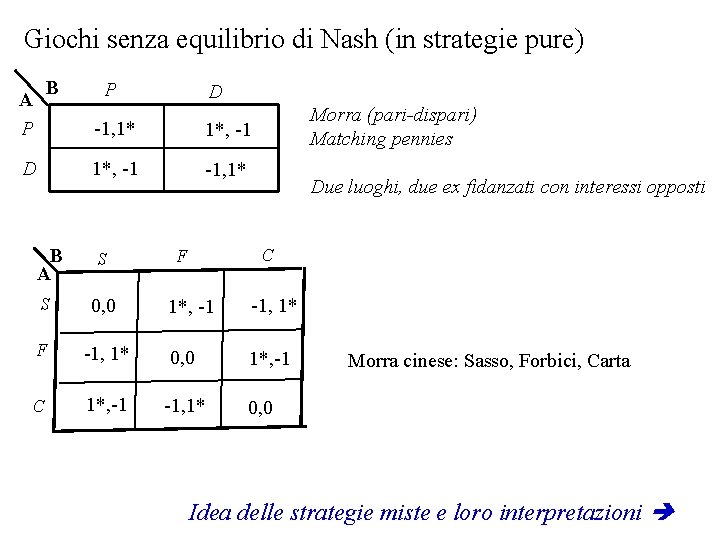
Giochi senza equilibrio di Nash (in strategie pure) B A P D -1, 1* 1*, -1 -1, 1* S Morra (pari-dispari) Matching pennies Due luoghi, due ex fidanzati con interessi opposti C F 1*, -1 -1, 1* 0, 0 1*, -1 -1, 1* S 0, 0 F C Morra cinese: Sasso, Forbici, Carta 0, 0 Idea delle strategie miste e loro interpretazioni

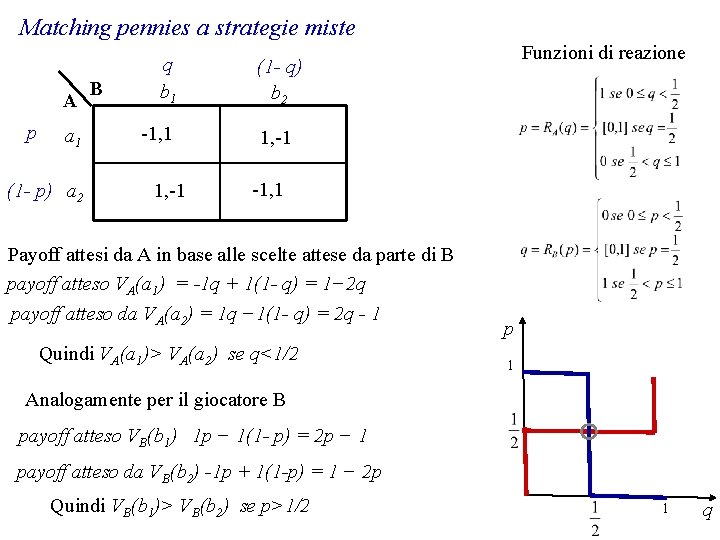
Matching pennies a strategie miste A p a 1 (1 - p) a 2 B q b 1 -1, 1 1, -1 Funzioni di reazione (1 - q) b 2 1, -1 -1, 1 Payoff attesi da A in base alle scelte attese da parte di B payoff atteso VA(a 1) = -1 q + 1(1 - q) = 1− 2 q payoff atteso da VA(a 2) = 1 q − 1(1 - q) = 2 q - 1 Quindi VA(a 1)> VA(a 2) se q<1/2 p 1 Analogamente per il giocatore B payoff atteso VB(b 1) 1 p − 1(1 - p) = 2 p − 1 payoff atteso da VB(b 2) -1 p + 1(1 -p) = 1 − 2 p Quindi VB(b 1)> VB(b 2) se p>1/2 1 q

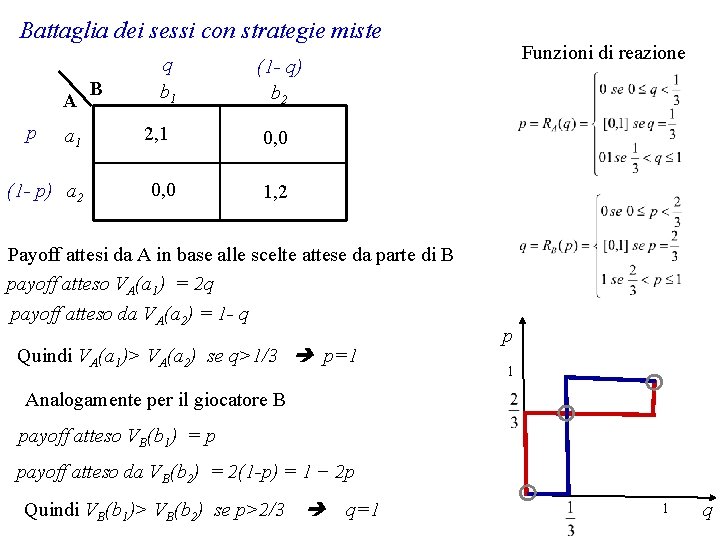
Battaglia dei sessi con strategie miste A p a 1 (1 - p) a 2 B q b 1 2, 1 0, 0 Funzioni di reazione (1 - q) b 2 0, 0 1, 2 Payoff attesi da A in base alle scelte attese da parte di B payoff atteso VA(a 1) = 2 q payoff atteso da VA(a 2) = 1 - q Quindi VA(a 1)> VA(a 2) se q>1/3 p=1 p 1 Analogamente per il giocatore B payoff atteso VB(b 1) = p payoff atteso da VB(b 2) = 2(1 -p) = 1 − 2 p Quindi VB(b 1)> VB(b 2) se p>2/3 q=1 1 q

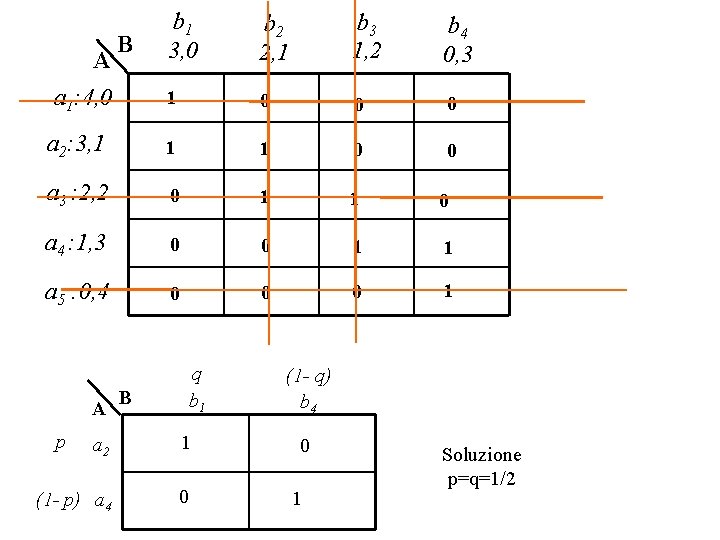
Gioco degli aiuti umanitari Due paesi ricchi hanno sovrabbondanza di beni rapidamente deteriorabili (es. alimentari) e decidono di regalarli a paesi poveri per ottenere un’influenza politica o alleanza in caso di conflitto. Due i paesi beneficiari, I e II; 4 e 3 le unità di beni a disposizione di A e B risp. Se un paese ricco dà a uno povero più unità del bene se ne assicura il controllo (+1) se meno perde il controllo (-1) se uguale neutralità (0). Può A sfruttare il vantaggio (4 contro 3) per controllarli entrambi? A a 1: 4, 0 B b 1 3, 0 b 2 2, 1 b 3 1, 2 b 4 0, 3 1 0 0 Payoff di A: somma algebrica dei controlli a 2: 3, 1 1 1 0 gioco a somma 0 a 3 : 2, 2 0 1 1 0 a 4 : 1, 3 0 0 1 1 a 5 : 0, 4 0 0 0 1

b 1 3, 0 b 2 2, 1 b 3 1, 2 b 4 0, 3 1 0 0 0 a 2: 3, 1 1 1 0 0 a 3 : 2, 2 0 1 1 0 a 4 : 1, 3 0 0 1 1 a 5 : 0, 4 0 0 0 1 A B a 1: 4, 0 A p B q b 1 a 2 1 (1 - p) a 4 0 (1 - q) b 4 0 1 Soluzione p=q=1/2

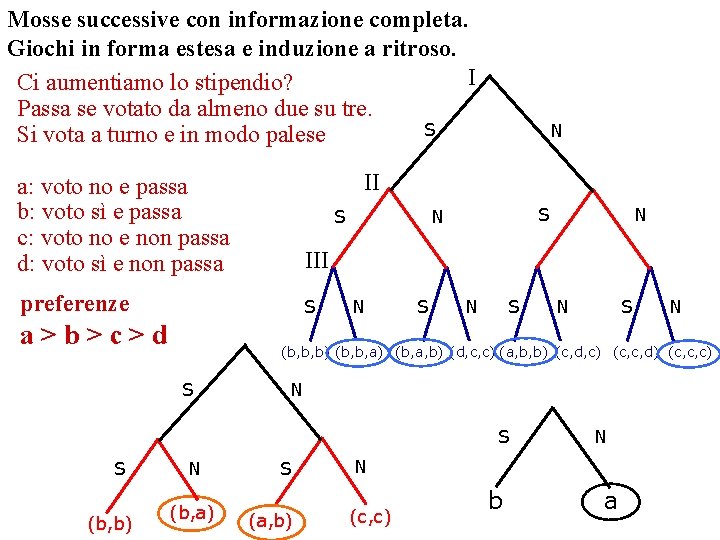
Mosse successive con informazione completa. Giochi in forma estesa e induzione a ritroso. I Ci aumentiamo lo stipendio? Passa se votato da almeno due su tre. S Si vota a turno e in modo palese II a: voto no e passa b: voto sì e passa c: voto no e non passa d: voto sì e non passa III preferenze S a>b>c>d N S S N S (b, b) N N (b, b, b) (b, b, a) (b, a, b) (d, c, c) (a, b, b) (c, d, c) (c, c, d) (c, c, c) S S N N (b, a) S (a, b) N N (c, c) b a

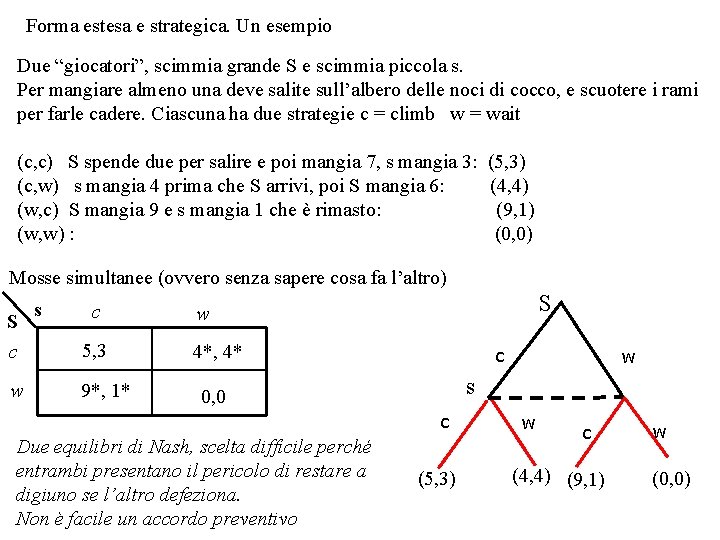
Forma estesa e strategica. Un esempio Due “giocatori”, scimmia grande S e scimmia piccola s. Per mangiare almeno una deve salite sull’albero delle noci di cocco, e scuotere i rami per farle cadere. Ciascuna ha due strategie c = climb w = wait (c, c) S spende due per salire e poi mangia 7, s mangia 3: (c, w) s mangia 4 prima che S arrivi, poi S mangia 6: (w, c) S mangia 9 e s mangia 1 che è rimasto: (w, w) : (5, 3) (4, 4) (9, 1) (0, 0) Mosse simultanee (ovvero senza sapere cosa fa l’altro) S c w s c 5, 3 9*, 1* S w 4*, 4* c s 0, 0 c Due equilibri di Nash, scelta difficile perché entrambi presentano il pericolo di restare a digiuno se l’altro defeziona. Non è facile un accordo preventivo w (5, 3) w c (4, 4) (9, 1) w (0, 0)

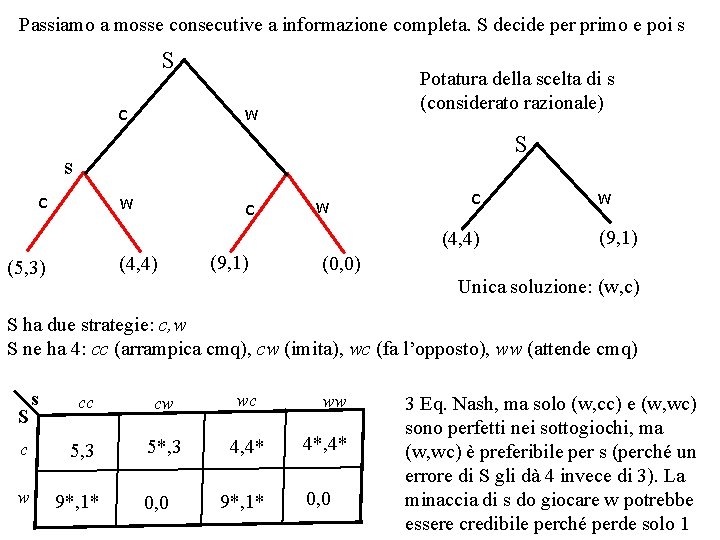
Passiamo a mosse consecutive a informazione completa. S decide per primo e poi s S c Potatura della scelta di s (considerato razionale) w S s c w c (4, 4) (5, 3) (9, 1) w (9, 1) (0, 0) Unica soluzione: (w, c) S ha due strategie: c, w S ne ha 4: cc (arrampica cmq), cw (imita), wc (fa l’opposto), ww (attende cmq) s cc cw wc c 5, 3 5*, 3 4, 4* w 9*, 1* S 0, 0 9*, 1* ww 4*, 4* 0, 0 3 Eq. Nash, ma solo (w, cc) e (w, wc) sono perfetti nei sottogiochi, ma (w, wc) è preferibile per s (perché un errore di S gli dà 4 invece di 3). La minaccia di s do giocare w potrebbe essere credibile perché perde solo 1

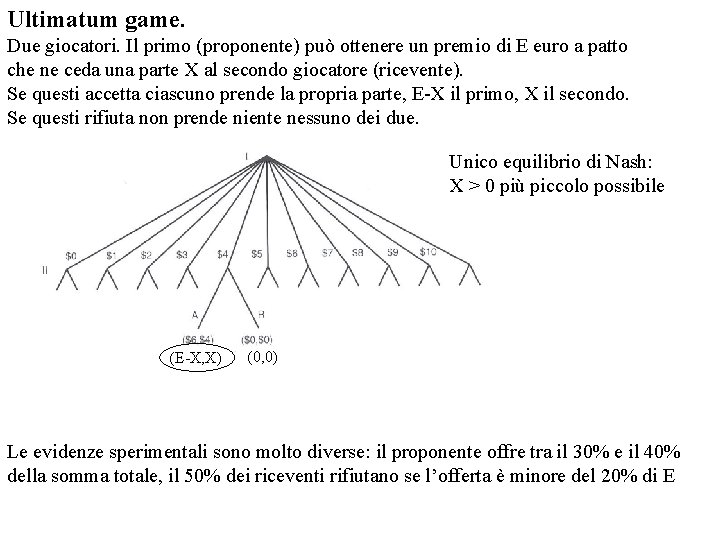
Ultimatum game. Due giocatori. Il primo (proponente) può ottenere un premio di E euro a patto che ne ceda una parte X al secondo giocatore (ricevente). Se questi accetta ciascuno prende la propria parte, E-X il primo, X il secondo. Se questi rifiuta non prende niente nessuno dei due. Unico equilibrio di Nash: X > 0 più piccolo possibile (E-X, X) (0, 0) Le evidenze sperimentali sono molto diverse: il proponente offre tra il 30% e il 40% della somma totale, il 50% dei riceventi rifiutano se l’offerta è minore del 20% di E

Dictator Game (o di puro altruismo) Il proponente ha la possibilità (non l’obbligo) di donare una parte al ricevente, senza avere ritorsioni. Le evidenze sperimentali mostrano che X è tra il 10% e il 25% se i due giocatori si conoscono. Invece in caso di doppio anonimato il 70% circa non lascia nulla e il rimanente tra il 10% e il 20% Behavioral economics (Economia comportamentale)

Asta da un dollaro Si mettono all’asta 100 euro, partendo da un’offerta iniziale di 1 €. Chi offre di più si aggiudica i 100 euro, ma anche chi fa la seconda offerta paga, senza però vincere nulla. …proviamo… all’inizio sembra una buona opportunità… ai 50 euro ci si rende conto che il banditore ha fatto un affare … ai 99 euro si vorrebbe smettere ma… conviene offrire 100 e poi 101… se non vogliamo perdere tutto… aste realmente effettuare sono arrivate a 300 -350 euro, con un guadagno del 700% da parte del banditore !!! Si tratta della tipica situazione in cui il vincitore paga un prezzo sproporzionato rispetto al premio che ottiene, lo sconfitto paga un alto prezzo per una battaglia che non frutta nulla. Morale: era meglio non iniziare

Premio Nobel, 1994 "for their pioneering analysis of equilibria in theory of non-cooperative games" Harsanyi Nash Selten Premio Nobel, 2005 "for having enhanced our understanding of conflict and cooperation through game-theory analysis" Aumann Schelling

Premio Nobel Economia, 2007 "for having laid the foundations of mechanism design theory" Myerson Maskin Hurwicz Nobel 2012 “per le loro ricerche sulla teoria dei giochi applicata al funzionamento dei mercati. Shapley Roth

Alcune letture Roberto Lucchetti “Scacchi e scimpanzé” Bruno Mondadori 2012 Pierluigi Argoneto “I Radiohead, l’arcobaleno e il piede sinistro di Dio”, Armando Editore 2009 Roberto Lucchetti “Passione per Trilli” Springer Italia 2007 Fioravante Patrone “Decisori (razionali) interagenti”, Plus edizioni 2006 Tom Siegfried “E’ la matematica, bellezza!”, Bollati Boringhieri 2006