Corso di Teoria delle Decisioni Esercitazioni Lezione 1

Corso di Teoria delle Decisioni Esercitazioni Lezione 1 – 15/09/04 Docente: S. Moretti http: //www. dima. unige. it/~moretti/

Paradossi in Teoria delle Decisioni • • Cosa significa paradosso? Definizione dal dizionario Webster – “An apparently sound argument leading to a contradiction. ” • • Perche’ studiarli? Statistical paradox: It is quite possible to draw wrong conclusions from correlation. For example, towns with a larger number of churches generally have a higher crime rate - because both result from higher population.

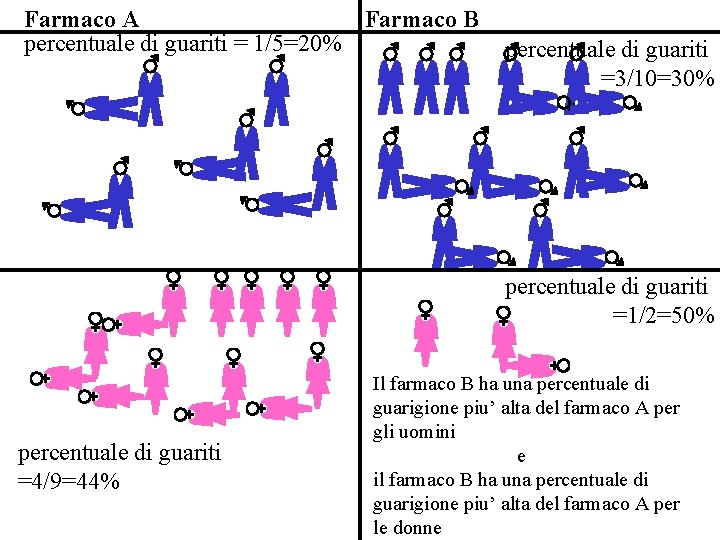
Paradosso di Simpson A e B reppresentano due farmaci per combattere una malattia terribile. Nel seguente studio sono state considerate 26 persone con tale malattia, alcune sono state trattate con il farmaco A, altre con quello B. I dati raccolti dallo studio sono riportati di seguito • 1 uomo trattato con A e’ guarito. • 4 uomini trattati con A non sono guariti. • 4 donne trattate con A sono guarite. • 5 donne trattate con A non sono guarite. • 3 uomini trattati con B sono guariti. • 7 uomini trattati con B non sono guariti. • 1 donna trattata con B e’ guarita. • 1 donna trattata con B non e’ guarita.

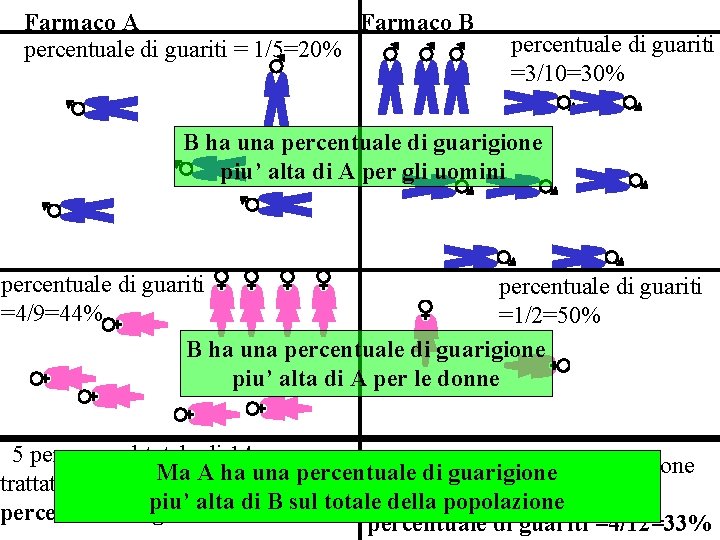
Farmaco A Farmaco B percentuale di guariti = 1/5=20% percentuale di guariti =3/10=30% percentuale di guariti =1/2=50% percentuale di guariti =4/9=44% Il farmaco B ha una percentuale di guarigione piu’ alta del farmaco A per gli uomini e il farmaco B ha una percentuale di guarigione piu’ alta del farmaco A per le donne

Farmaco A Farmaco B percentuale di guariti = 1/5=20% percentuale di guariti =3/10=30% B ha una percentuale di guarigione piu’ alta di A per gli uomini percentuale di guariti =4/9=44% percentuale di guariti =1/2=50% B ha una percentuale di guarigione piu’ alta di A per le donne 5 persone sul totale di 14 persone sul totale di 12 persone Ma A ha una percentuale di guarigione trattate con A sono guarite. trattate con B sono guarite. piu’ alta di B sul totale della popolazione percentuale di guariti=5/14=36% percentuale di guariti =4/12=33%

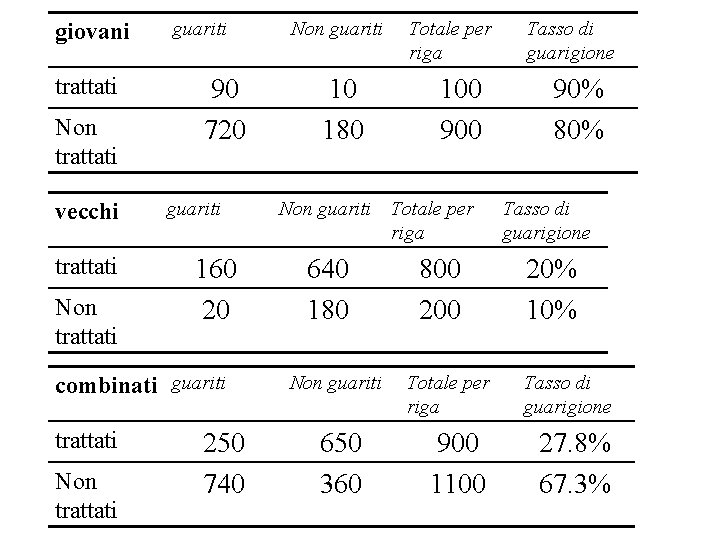
giovani trattati Non trattati vecchi trattati Non trattati guariti 90 720 guariti 160 20 combinati guariti trattati Non trattati 250 740 Non guariti 10 180 Totale per riga 100 900 Non guariti Totale per riga 640 180 Non guariti 650 360 800 200 Tasso di guarigione 90% 80% Tasso di guarigione 20% 10% Totale per riga Tasso di guarigione 900 1100 27. 8% 67. 3%

• Come si spiega il paradosso di Simpson in questo caso? – La spiegazione potrebbe essere: la malattia e’ molto piu’ grave nei vecchi che nei giovani, nel senso che la percentuale di guarigione e’ sempre molto minore nei vecchi che nei giovani, trattati o meno. Inoltre I pazienti trattati (900) sono quasi tutti vecchi(800 su 900, l’ 88. 9%). Quindi I pazienti trattati guariscono meno di quelli non trattati non per effetto del farmaco ma semplicemente peche’ sono piu’ vecchi. • Piu’ in generale quindi, e’ buona norma considerare tutta l’informazione disponibile sulla situazione da modellizzare per rendersi conto di quali associazioni siano sensate e quali associazioni siano “spurie. ” • Open Questions: e’ sempre possibile seguire questa buona norma? Qual e’ il modo corretto di procedere per l’assunzione di un modello statistico?

Il paradosso di Simpson “segue” dal fatto che possa essere soddisfatto il seguente sistema: a/b < A/B, c/d < C/D (a + c)/(b + d) > (A + C)/(B + D). ESERCIZIO 1: • Che cosa devono rappresentare le variabili del sistema precedente per spiegare perche’ ci si puo’ imbattare nel Paradosso di Simpson (dirlo sull’esempio vecchi/giovani)? • Nell’esempio delle classi di vecchi/giovani e’ possibile, almeno aritmeticamente, che si presenti il paradosso di Simpson quando il trattamento e’ efficace sia nei vecchi che nei giovani con una percentuale di guarigione nei trattati del 50% e 95% rispettivamente (modificando opportunamente i dati relativi nelle tabelle in modo che presentino tali percentuali di guarigione)?

Una giornata di beneficienza Guadagno dell’associazione benefica senza assicurazione Guadagni Brutto Bel tempo Evento sportivo Festa campale Guadagno dell’associazione benefica con assicurazione (premio 10, copertura 50) Guadagni Brutto Bel tempo 85 120 75 150 Evento sportivo Festa campale 125 110 115 140 • Il presidente considera la tabella di sinistra, l’evento sportivo garantisce almeno 85 mentre la festa puo’ garantire soltanto 75. Nota quindi che sarebbe meglio scegliere l’evento sportivo • Il presidente considera la tabella di sinistra, l’evento sportivo garantisce almeno 110 mentre la festa puo’ garantire soltanto 115. Nota quindi che sarebbe meglio scegliere la festa campale

Una giornata di beneficienza (2) Guadagno dell’associazione benefica senza assicurazione Guadagni Brutto Bel tempo Evento sportivo Festa campale Guadagno dell’associazione benefica con assicurazione (premio 10, policy 50) Guadagni Brutto Bel tempo 85 120 75 150 Evento sportivo Festa campale 125 110 115 140 • La segretaria dell’associazione fa notare che non ci sono differenze tra le due tabelle. In entrambi I casi l’evento sportivo fa guadagnare 10 in piu’ nel caso di brutto tempo e 30 in meno nel caso di tempo bello. • Quindi non e’ consistente raccomandare l’evento sportivo sulla base della tabella di sinistra e la festa campale sulla base della tabella di destra.

Una giornata di beneficienza (3) Guadagni Brutto Bel tempo Evento sportivo 85 120 Evento sportivo 125 110 Festa campale 75 150 Festa campale 115 140 Bisognerebbe considerare la possibilita’ di perdita di guadagno (o rimpianto) di un opzione, cioe’ l’ammontare di denaro perso rispetto l’alternativa ottima per la circostanza che si presenta Rimpianti Evento sportivo Festa campale Brutto tempo 0 10 Bel tempo 30 0 Massimo rimpianto 30 10

Una giornata di beneficienza (4) • Ma allora bisogna organizzare la festa che ha un rimpianto massimo piu’ piccolo? Vada per la festa campale… • Il tesoriere chiede se devono assicurarsi o meno • Ci si accorge che in realta’ ci sono 4 opzioni non soltanto 2. Rimpianti Brutto tempo Bel tempo Massimo rimpianto Evento sportivo senza assicurazione 85(40) 120(30) 40 Festa campale senza assicurazione 75(50) 150(0) 50 Evento sportivo con assicurazione 125(0) 110(40) 40 115(10) 140(10) 10 Festa campale con assicurazione • Si sceglie di fare la festa campale facendo l’assicurazione.

Una giornata di beneficienza (5) • Il metodo di decisione scelto e’ detto del minimax rimpianto. • L’obiettivo e’ quello di scegliere l’opzione che minimizza il massimo rimpianto. ESERCIZIO 2: Che scelta fareste, sulla base del metodo di minimax rimpianto se vi accorgeste che l’assicurazione non e’ piu’ valida? Quale tabella utilizzereste per la vostra decisione?

ESERCIZIO 3: Scegliere l’opzione ottimale secondo il criterio del minimax rimpianto. Da solo Guadagni Brutto In societa’ con altri Bel tempo Discoteca Gelateria 120 45 Guadagni Brutto Bel tempo 70 110 Discoteca Gelateria 130 35 40 140

Indipendenza delle preferenze • Si supponga di dover scegliere il proprio pasto da un menu’ fisso piuttosto limitato quale – Primo • polenta oppure spaghetti – Secondo • pesce oppure bistecca • Si supponga che io faccia la mia scelta assegnando un punteggio ai singoli piatti, sommando i punteggi e quindi scegliendo il pasto che risulta avere il massimo punteggio. • Le mie preferenze per i piatti singoli sarebbero – – Polenta Spaghetti Pesce Bistecca 10 8 9 2

• Quindi i 4 possibili menu’ che ne seguirebbero sono –polenta e pesce 19 –polenta e bistecca 12 –Spaghetti e pesce 17 –Spaghetti e bistecca 10 • Sembrerebbe quindi che io preferisca polenta e pesce per il mio pasto. • In realta’ non amo mischiare sapori di mare e con quelli dei monti… • La ragione per cui il punteggio totale non rappresenta le mie vere preferenze e’ che all’inizio avevo assunto che le mie preferenze per il “secondo” fossero independenti da quelle per il “primo”: non e cosi’. • Solo quando le preferenze sono “indipendenti” uno riesce ad ottenerle facendo le somme dei punteggi.

Money pump • Perche’ la Td. D da’ cosi’ tanta importanza alla transitivita’ delle preferenze? • Il decisore ha preferenze su R X, dove R rappresentano somme di denaro (in euro) e X={mela, arancia, pera} tali che (0, mela) (0, arancia) ; (0, arancia) (0, pera) ; (0, pera) (0, mela) • Per quel che riguarda il denaro le preferenze sono standard, maggiore denaro e’ meglio. • Per afferrare meglio l’idea, si assume che le preferenze sui frutti rimangano tali anche dietro pagamento di piccole quote di denaro, per esempio (-0. 1, mela) (0, arancia) ; (-0. 1, arancia) (0, pera) ; (-0. 1, pera) (0, mela)

Money pump (2) • Se siete cosi’ fortunati da incontrare un decisore con tali preferenze, accertatevi subito di avere una mela, un’arancia e una pera (altrimenti correte a comprarle!) • Regalategli un’arancia • Allora gli si puo’ dire: ”guarda io ho una mela, mentre tu hai un’arancia. Posso darti una mela purche’ tu mi dia indietro l’arancia, insieme a 0. 1 euro”. • In base alle preferenze del decisore, egli desiderera’ fare lo scambio. • Naturalmente, immediatamente dopo si puo’ ricominciare: “hey, io ho una pera. . . ” • Con questo “money pump” voi diventere ricchi a spese del decisore. . . SPUNTO PER LA RIFLESSIONE: Vi e’ mai capitato di osservare situazioni reali simili o almeno riconducibili in parte al meccanismo della money pump?