les Lois de Kpler K 1 loi des

les Lois de Képler

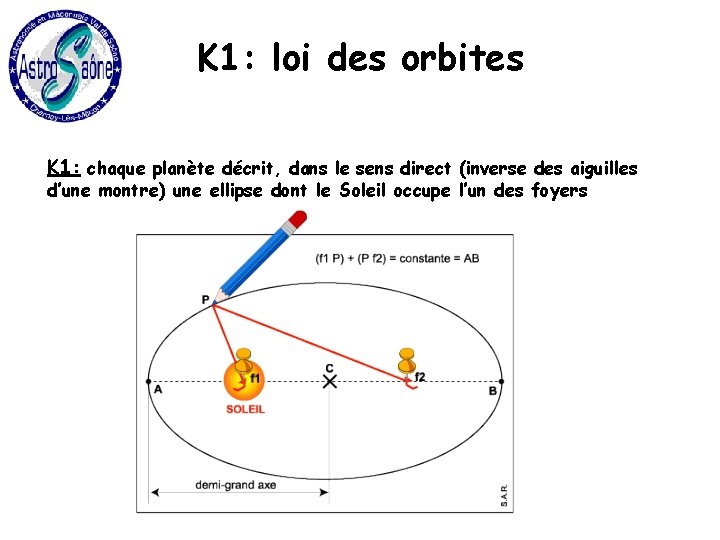
K 1: loi des orbites K 1: chaque planète décrit, dans le sens direct (inverse des aiguilles d’une montre) une ellipse dont le Soleil occupe l’un des foyers

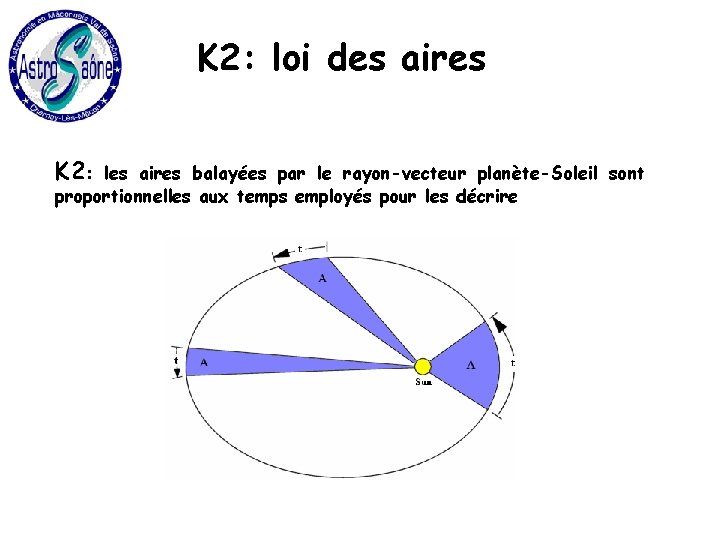
K 2: loi des aires K 2: les aires balayées par le rayon-vecteur planète-Soleil sont proportionnelles aux temps employés pour les décrire

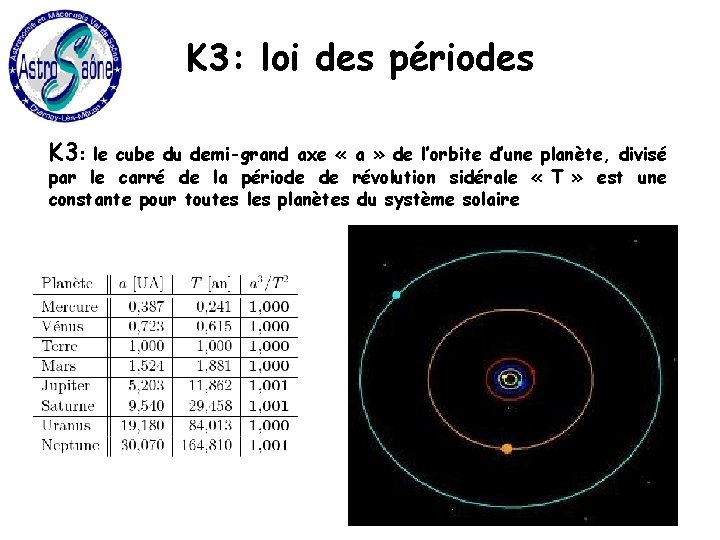
K 3: loi des périodes K 3: le cube du demi-grand axe « a » de l’orbite d’une planète, divisé par le carré de la période de révolution sidérale « T » est une constante pour toutes les planètes du système solaire

Démarche de Képler • ses « convictions » initiales: • du Soleil émane la « force motrice » des planètes • les mouvements planétaires ont une cause physique (et non animiste) • essaye de faire coller les observations de Tycho avec un modèle d’orbite • il tient son « journal » , son « blog » !! • raconte ses hypothèses, ses doutes, ses erreurs démarche de « scientifique » moderne

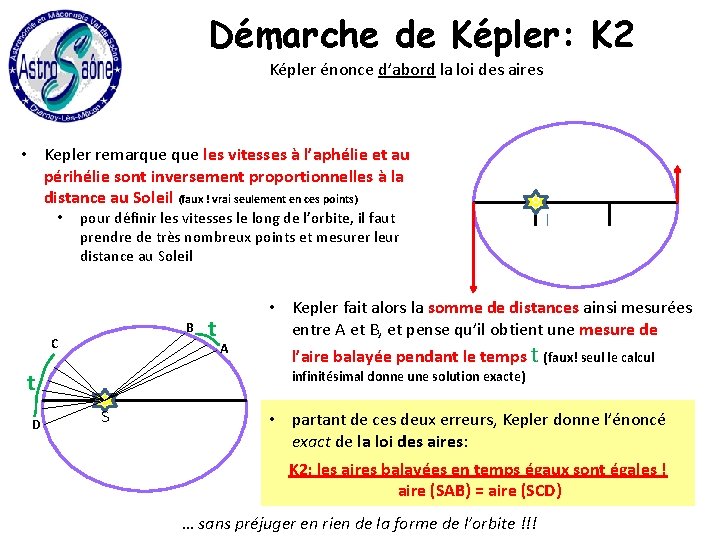
Démarche de Képler: K 2 Képler énonce d’abord la loi des aires • Kepler remarque les vitesses à l’aphélie et au périhélie sont inversement proportionnelles à la distance au Soleil (faux ! vrai seulement en ces points) • pour définir les vitesses le long de l’orbite, il faut prendre de très nombreux points et mesurer leur distance au Soleil B C t D t A 8 • Kepler fait alors la somme de distances ainsi mesurées entre A et B, et pense qu’il obtient une mesure de l’aire balayée pendant le temps t (faux! seul le calcul infinitésimal donne une solution exacte) 8 S S • partant de ces deux erreurs, Kepler donne l’énoncé exact de la loi des aires: K 2: les aires balayées en temps égaux sont égales ! aire (SAB) = aire (SCD) … sans préjuger en rien de la forme de l’orbite !!!

Démarche de Képler: K 1 Képler revient au modèle d’orbite (1603) • Kepler sait qu’il doit s’affranchir de la circularité; il choisit le modèle qui s’en rapproche le plus: l’ovale !! …. et pour cela, n’hésite pas à réintroduire des épicycles !! « jamais un scientifique n’a encore pondu un tel œuf ! » S • il fait la somme de 180 distances Soleil-Mars !! nouvel échec M

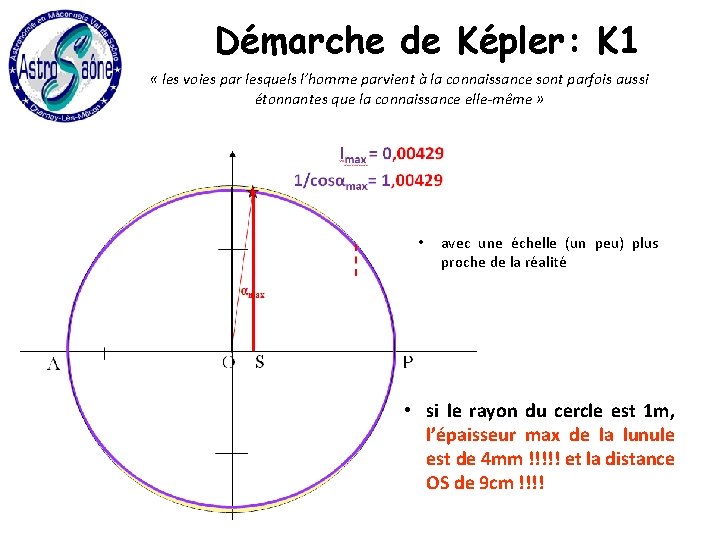
Démarche de Képler: K 1 « les voies par lesquels l’homme parvient à la connaissance sont parfois aussi étonnantes que la connaissance elle-même » • • en étudiant les lunules qui distinguent la trajectoire de Mars du cercle circonscrit, Kepler remarque par hasard que l’épaisseur maximale de la lunule est de 0, 00429, alors que 1/cosα = 1, 00429 incroyable coïncidence !! 5 chiffres après la virgule !! • d’autant que notre figure est loin d’être à l’échelle !

Démarche de Képler: K 1 « les voies par lesquels l’homme parvient à la connaissance sont parfois aussi étonnantes que la connaissance elle-même » • avec une échelle (un peu) plus proche de la réalité • si le rayon du cercle est 1 m, l’épaisseur max de la lunule est de 4 mm !!!!! et la distance OS de 9 cm !!!!

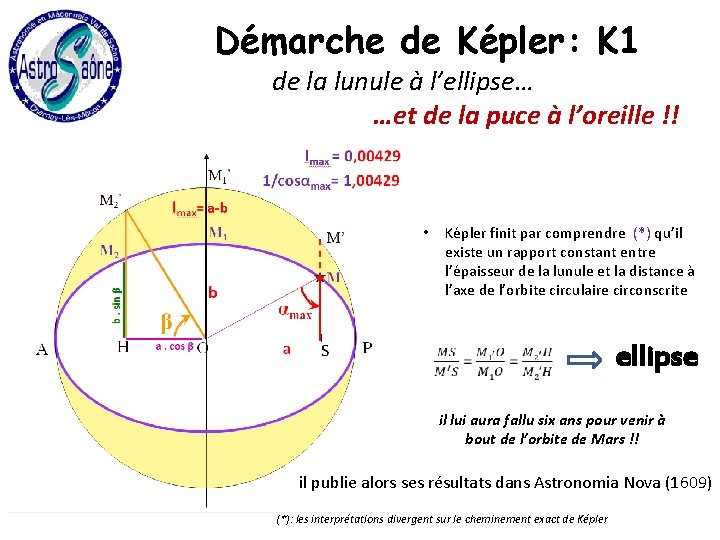
Démarche de Képler: K 1 de la lunule à l’ellipse… …et de la puce à l’oreille !! Képler finit par comprendre (*) qu’il existe un rapport constant entre l’épaisseur de la lunule et la distance à l’axe de l’orbite circulaire circonscrite • ellipse il lui aura fallu six ans pour venir à bout de l’orbite de Mars !! nouvel échecil publie alors ses résultats dans Astronomia Nova (1609) (*): les interprétations divergent sur le cheminement exact de Képler

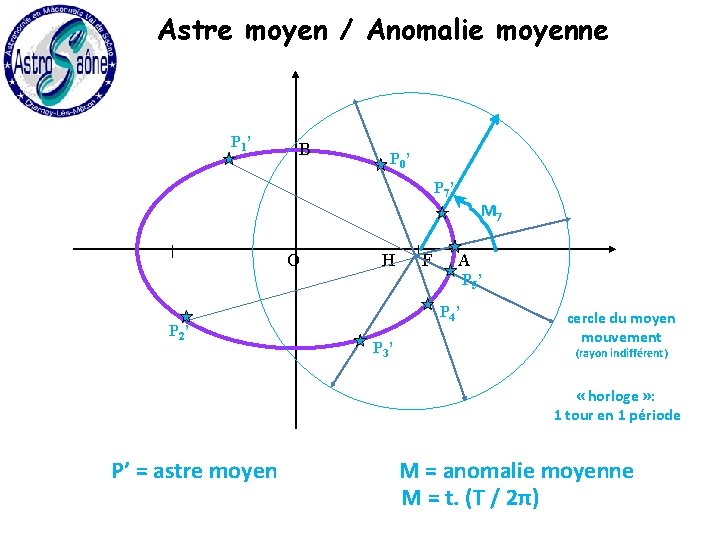
Astre moyen / Anomalie moyenne P 1’ B P 0’ P 7’ O H F M 7 A P 5’ P 2’ P 4’ P 3’ cercle du moyen mouvement (rayon indifférent) « horloge » : 1 tour en 1 période P’ = astre moyen M = anomalie moyenne M = t. (T / 2π)

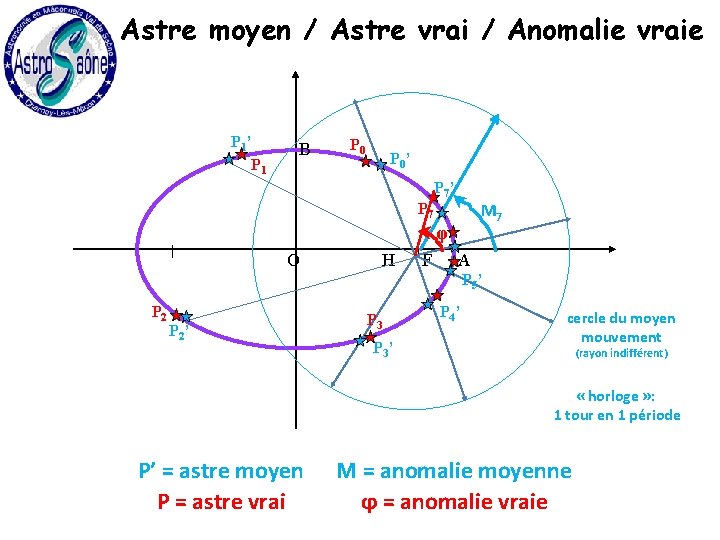
Astre moyen / Astre vrai / Anomalie vraie P 1’ P 1 B P 0’ P 7’ M 7 P 7 φ O H F A P 5’ P 2’ P 3’ P 4’ cercle du moyen mouvement (rayon indifférent) « horloge » : 1 tour en 1 période P’ = astre moyen P = astre vrai M = anomalie moyenne ϕ = anomalie vraie

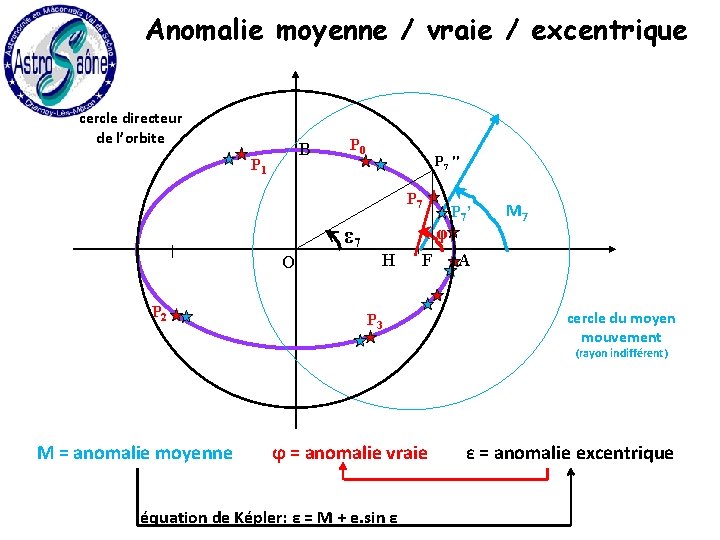
Anomalie moyenne / vraie / excentrique cercle directeur de l’orbite B P 1 P 0 P 7 " P 7 ε 7 O P 2 φ H F P 3 P 7’ M 7 A cercle du moyen mouvement (rayon indifférent) M = anomalie moyenne ϕ = anomalie vraie équation de Képler: ε = M + e. sin ε ε = anomalie excentrique

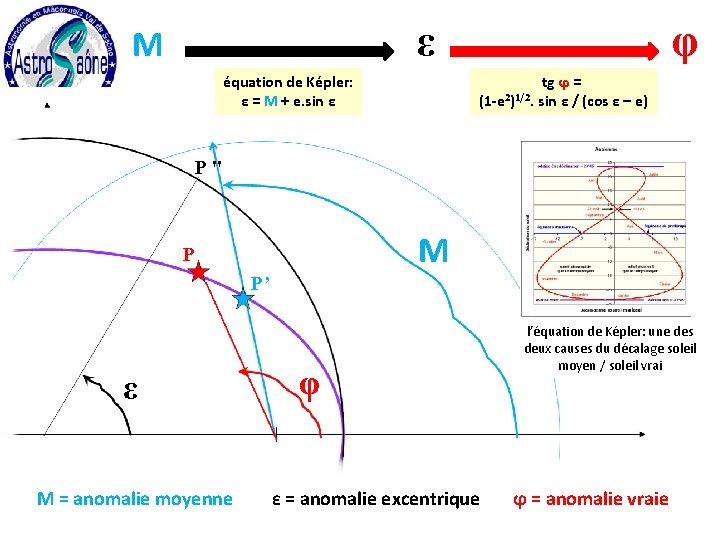
ε M équation de Képler: ε = M + e. sin ε φ tg ϕ = (1 -e 2)1/2. sin ε / (cos ε – e) P " M P P’ ε M = anomalie moyenne φ ε = anomalie excentrique l’équation de Képler: une des deux causes du décalage soleil moyen / soleil vrai ϕ = anomalie vraie

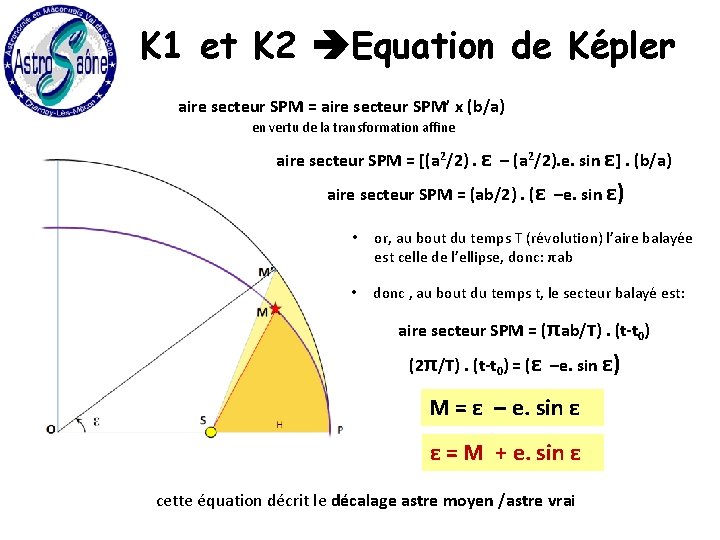
K 1 et K 2 Equation de Képler aire secteur SPM’ = secteur circ. OPM’ – triangle OSM’ aire cercle = πa 2 secteur: (πa 2). (ε/2 π) avec: OS = a. e et M’H = a. sin ε aire secteur SPM’ = (a 2/2). ε – (a 2/2). e. sin ε où ε est exprimé en radians

K 1 et K 2 Equation de Képler aire secteur SPM = aire secteur SPM’ x (b/a) en vertu de la transformation affine aire secteur SPM = [(a 2/2). ε – (a 2/2). e. sin ε]. (b/a) aire secteur SPM = (ab/2). (ε –e. sin ε) • or, au bout du temps T (révolution) l’aire balayée est celle de l’ellipse, donc: πab • donc , au bout du temps t, le secteur balayé est: aire secteur SPM = (πab/T). (t-t 0) (2π/T). (t-t 0) = (ε –e. sin ε) M = ε – e. sin ε ε = M + e. sin ε cette équation décrit le décalage astre moyen /astre vrai

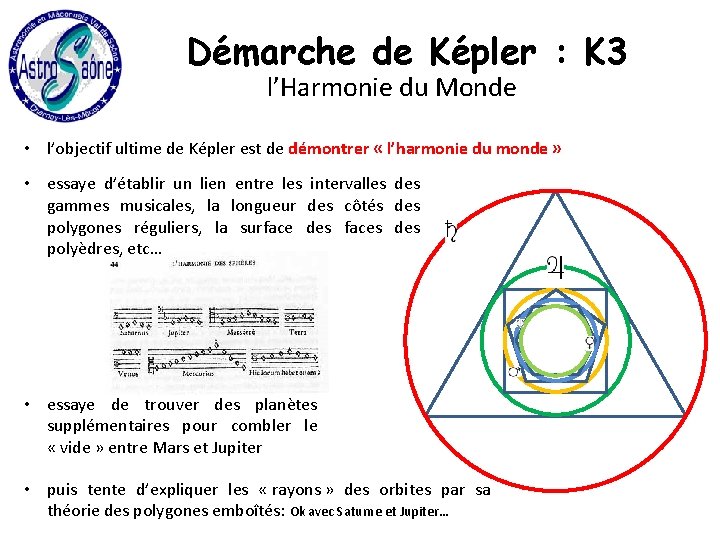
Démarche de Képler : K 3 l’Harmonie du Monde • l’objectif ultime de Képler est de démontrer « l’harmonie du monde » • essaye d’établir un lien entre les intervalles des gammes musicales, la longueur des côtés des polygones réguliers, la surface des faces des polyèdres, etc… • essaye de trouver des planètes supplémentaires pour combler le « vide » entre Mars et Jupiter • puis tente d’expliquer les « rayons » des orbites par sa théorie des polygones emboîtés: Ok avec Saturne et Jupiter…

Démarche de Képler : K 3 l’Harmonie du Monde • comme il ne réussit pas avec les polygones, il essaye les polyèdres emboîtés et leur sphères circonscrite et inscrite: nouvel échec • à force d’essais, Kepler trouve que le carré de la période de rotation des planètes est inversement proportionnel au cube du demi grand axe de l’orbite T 2/a 3 = constante • résultat empirique, qui prépare la voie à Newton • la troisième Loi n’est qu’un banal paragraphe de l’Harmonie du Monde (1619)

Newton 1642 - 1727 - réussit la synthèse des théories de Kepler, Descartes et Galilée - Newton utilise en particulier K 3 pour démontrer sa loi de gravitation universelle: F = G MM’ / D 2 - en retour, les lois de Newton permettent de démontrer K 1 et K 2 - mais Newton va au-delà de Képler: - découvre vraiment les phénomènes physiques que Képler recherchait - en démontre mathématiquement les implications (calcul différentiel et intégral) - rectifie les « erreurs » de Képler (*): inversion gravité (en 1/D) / inertie - étudie la dynamique des projectiles, vitesse de libération, etc… (*): sauf celle liée au sens direct de parcours des orbites

Démonstration des lois de Képler K 1: - géométrique (aire de triangles) - à partir de Newton et calcul différentiel K 2: - géométrique (Feynman) / hodographe - à partir de Newton et calcul différentiel - fait intervenir la notion de moment cinétique K 3: - équations aux dimensions - à partir principe gravitation universelle: a 3/T 2 = GM / 4π2 K 3 permet de calculer l’orbite géostationnaire: T= 23 h 56 mn 4 s si a = 42000 km h= 42000 – rayon terrestre ~ 36000 km