Lecture 3 kfn is Ofn for any positive

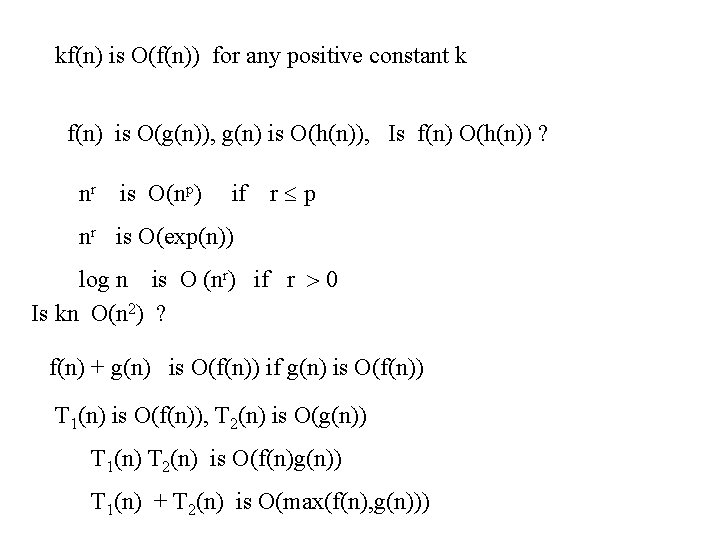










![Maxsubsum(A[], left, right) { if left = right, maxsum = max(A[left], 0); Center = Maxsubsum(A[], left, right) { if left = right, maxsum = max(A[left], 0); Center =](https://slidetodoc.com/presentation_image_h2/bdc34dad774bbb72b93ecd5cb3839b2d/image-13.jpg)






![Search(num, A[], left, right) { if (left = right) { if (A[left ]=num) return(left) Search(num, A[], left, right) { if (left = right) { if (A[left ]=num) return(left)](https://slidetodoc.com/presentation_image_h2/bdc34dad774bbb72b93ecd5cb3839b2d/image-20.jpg)


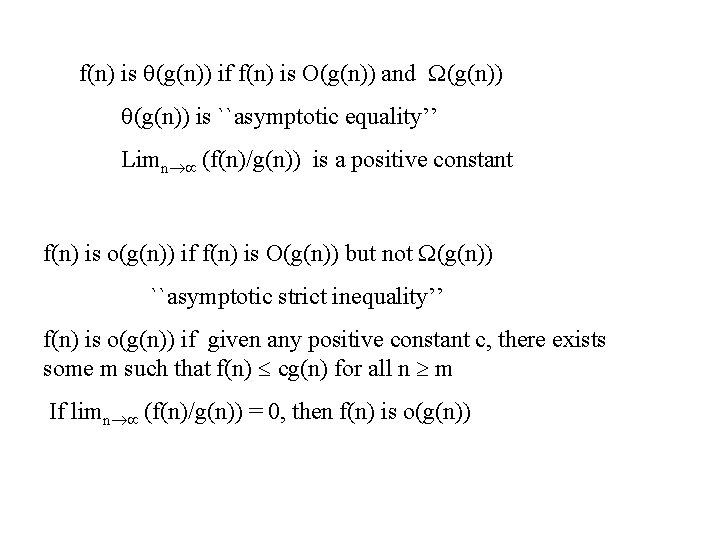




- Slides: 27

Lecture 3
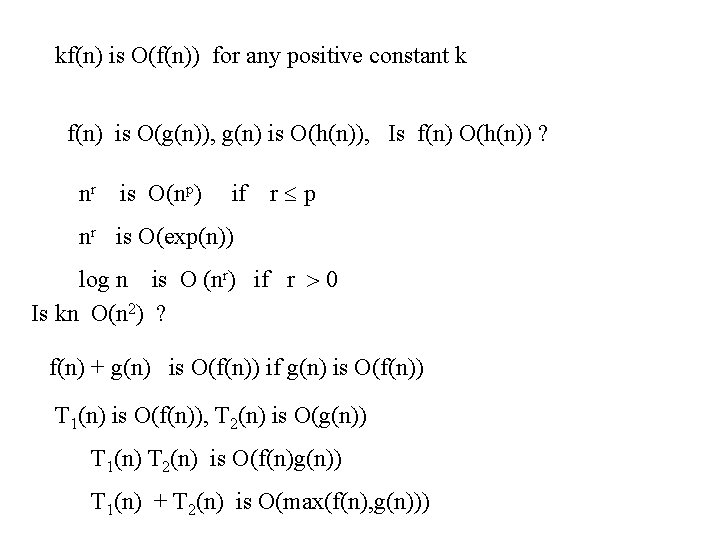
kf(n) is O(f(n)) for any positive constant k f(n) is O(g(n)), g(n) is O(h(n)), Is f(n) O(h(n)) ? nr is O(np) if r p nr is O(exp(n)) log n is O (nr) if r 0 Is kn O(n 2) ? f(n) + g(n) is O(f(n)) if g(n) is O(f(n)) T 1(n) is O(f(n)), T 2(n) is O(g(n)) T 1(n) T 2(n) is O(f(n)g(n)) T 1(n) + T 2(n) is O(max(f(n), g(n)))

Algorithm Complexity Analysis diff = sum = 0; For (k=0: k < N; k++) sum + 1; diff - 1; For (k=0: k < 3 N; k++) sum - 1;

First line takes 2 basic steps Every iteration of first loop takes 2 basic steps. First loop runs N times Every iteration of second loop takes 1 basic step Second loop runs for 3 N times Overall, 2 + 2 N + 3 N steps This is O(N)

Rules Complexity of a loop: O(Number of iterations in a loop * maximum complexity of each iteration) Nested Loops: Analyze the innermost loop first, complexity of next outer loop = number of iterations in this loop * complexity of inner loop, etc…. . sum = 0; For (i=0; i < N; i++) For (j=0; j < N; j++) sum + 1;

If (Condition) S 1 Else S 2 Maximum of the two If (yes) print(1, 2, …. 1000 N) Else print(1, 2, …. N 2)

Maximum Subsequence Problem There is an array of N elements Need to find i, j such that the sum of all elements between the ith and jth position is maximum for all such sums Maxsum = 0; For (i=0; i < N; i++) For (j=i; j < N; j++) { Thissum = sum of all elements between ith and jth positions; Maxsum = max(Thissum, Maxsum); }

Analysis Inner loop: j=i. N-1 (j-i + 1) = (N – i + 1)(N-i)/2 Outer Loop: i=0 N-1 (N – i + 1)(N-i)/2 = (N 3 + 3 N 2 + 2 N)/6

Maxsum = 0; For (i=0; i < N; i++) For (Thissum=0; j=i; j < N; j++) { Thissum = Thissum + A[i]; Maxsum = max(Thissum, Maxsum); } Complexity?

Divide and Conquer Break a big problem into two small sub-problems Solve each of them efficiently. Combine the two solutions

Maximum subsequence sum by divide and conquer Divide the array into two parts: left part, right part Max. subsequence lies completely in left, or completely in right or spans the middle. If it spans the middle, then it includes the max subsequence in the left ending at the last element and the max subsequence in the right starting from the center

4 – 3 5 – 2 -1 2 6 -2 Max subsequence sum for first half = 6 second half = 8 Max subsequence sum for first half ending at the last element is 4 Max subsequence sum for sum second half starting at the first element is 7 Max subsequence sum spanning the middle is ? Max subsequence spans the middle
![MaxsubsumA left right if left right maxsum maxAleft 0 Center Maxsubsum(A[], left, right) { if left = right, maxsum = max(A[left], 0); Center =](https://slidetodoc.com/presentation_image_h2/bdc34dad774bbb72b93ecd5cb3839b2d/image-13.jpg)
Maxsubsum(A[], left, right) { if left = right, maxsum = max(A[left], 0); Center = (left + right)/2 maxleftsum = maxsubsum(A[], left, center); maxrightsum = maxsubsum(A[], center+1, right); maxleftbordersum = 0; for (i=center; i>=left; i--) leftbordersum+=A[i]; Maxleftbordersum=max(maxleftbordersum, leftbordersum);

Find maxrightbordersum…. . return(maxleftsum, maxrightbordersum + maxleftbordersum);

Complexity Analysis T(1)=1 T(n) = 2 T(n/2) + cn = 2. cn/2 + 4 T(n/4) + cn = 4 T(n/4) + 2 cn = 8 T(n/8) + 3 cn =…………. . = 2 i. T(n/2 i) + icn =………………… (reach a point when n = 2 i i=log n = n. T(1) + cnlog n

n + cnlogn = O(nlogn)

Master Theorem T(1)=p T(n) = a. T(n/b) + cnk Case (1): a bk then T(n) is O(nlogba ) Case(2): a = bk then T(n) is O(nk logn) Case(3): a < bk then T(n) is O(nk ) Cormen, Leiserson, Rivest

Linear Complexity Algorithm Maxsum = 0; Thissum = 0; For (j=0; j<N; j++) { Thissum = Thissum + A[j]; If (Thissum 0), Thissum = 0; If (Maxsum Thissum), Maxsum = Thissum; } O(N) complexity

Binary Search You have a sorted list of numbers You need to search the list for the number If the number exists find its position. If the number does not exist you need to detect that
![Searchnum A left right if left right if Aleft num returnleft Search(num, A[], left, right) { if (left = right) { if (A[left ]=num) return(left)](https://slidetodoc.com/presentation_image_h2/bdc34dad774bbb72b93ecd5cb3839b2d/image-20.jpg)
Search(num, A[], left, right) { if (left = right) { if (A[left ]=num) return(left) and exit; else conclude NOT PRESENT and exit; } center = (left + right)/2 ; If (A[center] num) Search(num, A[], center + 1, right); If (A[center]>num) Search(num, A[], left, center ); If (A[center]=num) return(center) and exit; }

Complexity Analysis T(n) = T(n/2) + c O(log n) complexity

Other Complexity Notation Intuitively, (not exactly) f(n) is O(g(n)) means f(n) g(n) is an upper bound for f(n). Now a lower bound notation, (n) f(n) is (g(n)) if f(n) cg(n) for some positive constant c, and all large n. Limn (f(n)/g(n)) > 0
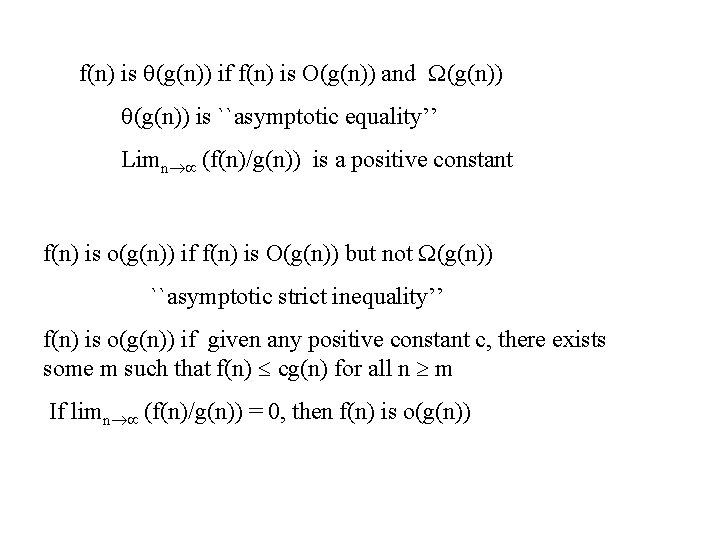
f(n) is (g(n)) if f(n) is O(g(n)) and (g(n)) is ``asymptotic equality’’ Limn (f(n)/g(n)) is a positive constant f(n) is o(g(n)) if f(n) is O(g(n)) but not (g(n)) ``asymptotic strict inequality’’ f(n) is o(g(n)) if given any positive constant c, there exists some m such that f(n) cg(n) for all n m If limn (f(n)/g(n)) = 0, then f(n) is o(g(n))

Asymptotically less than or equal to O Asymptotically greater than or equal to Asymptotically equal to Asymptotically strictly less o

Examples

Implication of the Notation Suppose, an algorithm has complexity (f(n)). This means that there exists a positive constant c such that for all sufficiently large n, there exists at least one input for which the algorithm consumes at least cf(n) steps.

Complexity of a Problem Vs Algorithm A problem is O(f(n)) means there is some O(f(n)) algorithm to solve the problem. A problem is (f(n)) means every algorithm that can solve the problem is (f(n))
 Kfn
Kfn 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad There are some cake
There are some cake Any to any connectivity
Any to any connectivity Informational probes adalah
Informational probes adalah Gram positive catalase positive cocci
Gram positive catalase positive cocci What's 8 + 5
What's 8 + 5 Positive practice positive outcomes
Positive practice positive outcomes Tobinskatten för och nackdelar
Tobinskatten för och nackdelar Hur ser ett referat ut
Hur ser ett referat ut Programskede byggprocessen
Programskede byggprocessen Karttecken färger
Karttecken färger Var finns arvsanlagen
Var finns arvsanlagen Shingelfrisyren
Shingelfrisyren Fuktmätningar i betong enlig rbk
Fuktmätningar i betong enlig rbk Formel för lufttryck
Formel för lufttryck Förklara densitet för barn
Förklara densitet för barn Elektronik för barn
Elektronik för barn Tack för att ni har lyssnat
Tack för att ni har lyssnat Smärtskolan kunskap för livet
Smärtskolan kunskap för livet Teckenspråk minoritetsspråk argument
Teckenspråk minoritetsspråk argument Typiska drag för en novell
Typiska drag för en novell Fimbrietratt
Fimbrietratt Trög för kemist
Trög för kemist Autokratiskt ledarskap
Autokratiskt ledarskap Humanitr
Humanitr Mindre än tecken
Mindre än tecken Toppslätskivling effekt
Toppslätskivling effekt