Kinematics Motion in One Dimension 2 1 Displacement












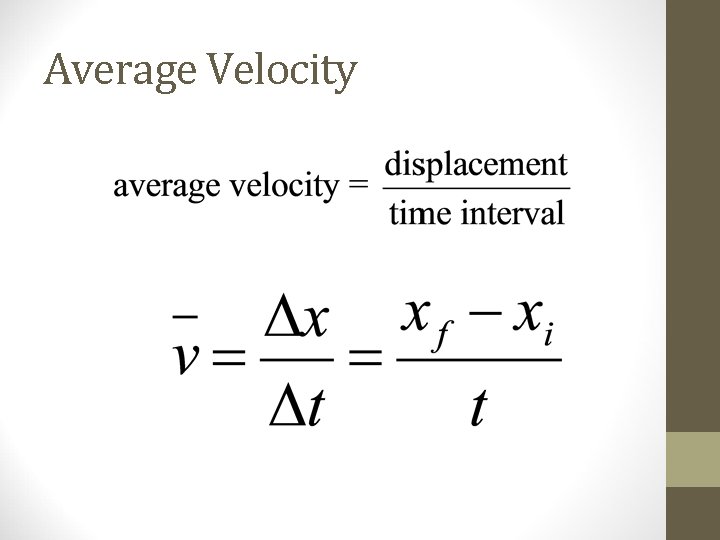












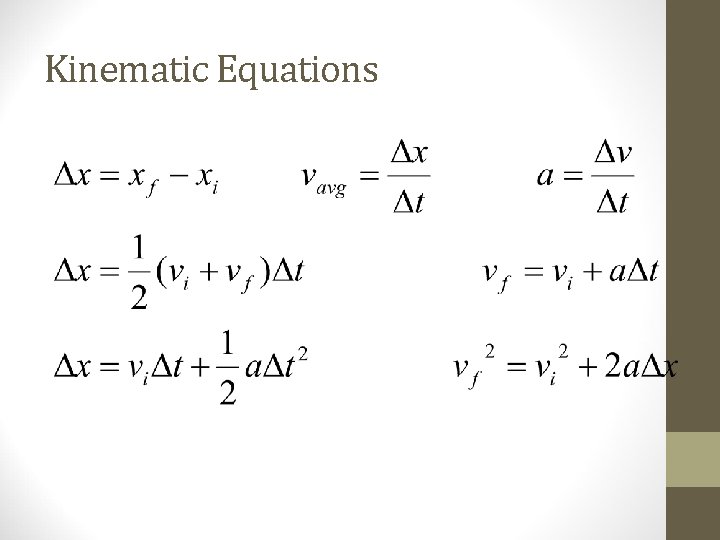










- Slides: 63

Kinematics: Motion in One Dimension

2. 1 Displacement & Velocity Learning Objectives • Describe motion in terms of displacement, time, and velocity • Calculate the displacement of an object traveling at a known velocity for a specific time interval • Construct and interpret graphs of position versus time

Essential Concepts • Frames of reference • Vector vs. scalar quantities • Displacement • Velocity – Average velocity – Instantaneous velocity • Acceleration • Graphical representation of motion

Reference Frames • Motion is relative • When we say an object is moving, we mean it is moving relative to something else (reference frame)

Scalar Quantities & Vector Quantities • • Scalar quantities have magnitude Example: speed 15 m/s Vector quantities have magnitude and direction Example: velocity 15 m/s North

Displacement •

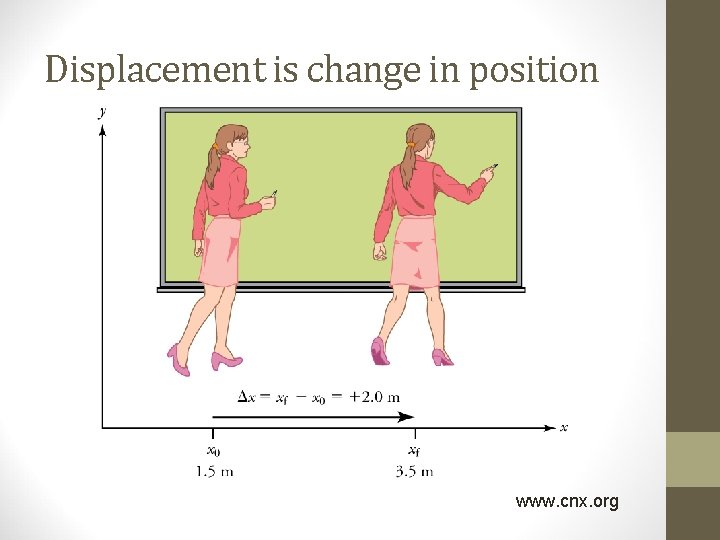
Displacement is change in position www. cnx. org

Displacement vs. Distance • Distance is the length of the path that an object travels • Displacement is the change in position of an object

Describing Motion Describing motion requires a frame of reference http: //www. sfu. ca/phys/100/lectures/lecture 5. html

Determining Displacement In these examples, position is determined with respect to the origin, displacement wrt x 1 http: //www. sfu. ca/phys/100/lectures/lecture 5. html

Indicating Direction of Displacement Direction can be indicated by sign, degrees, or geographical directions. When sign is used, it follows the conventions of a standard graph Positive Right Up Negative Left Down

Reference Frames & Displacement • Direction is relative to the initial position, x 1 • x 1 is the reference point

Average Velocity Speed: how far an object travels in a given time interval Velocity includes directional information:
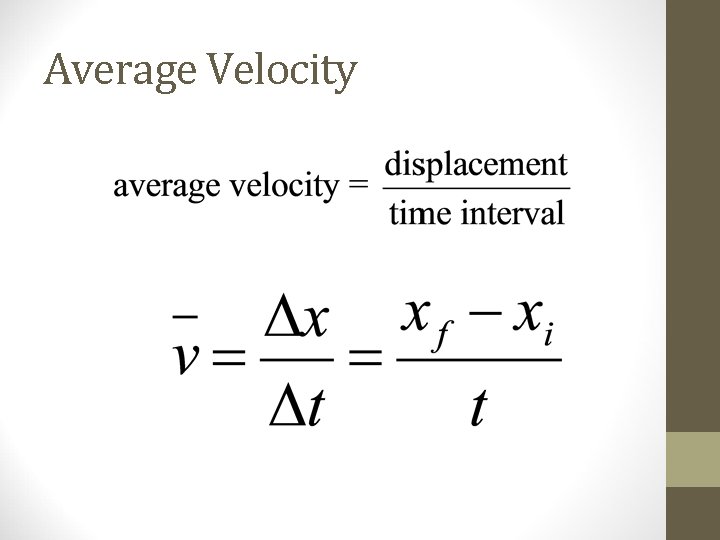
Average Velocity

Velocity • Example • A squirrel runs in a straight line, westerly direction from one tree to another, covering 55 meters in 32 seconds. Calculate the squirrel’s average velocity • vavg = ∆x / ∆t • vavg = 55 m / 32 s • vavg = 1. 7 m/s west

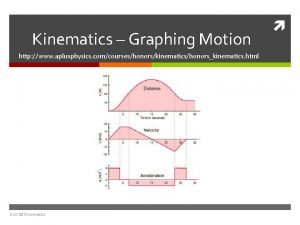
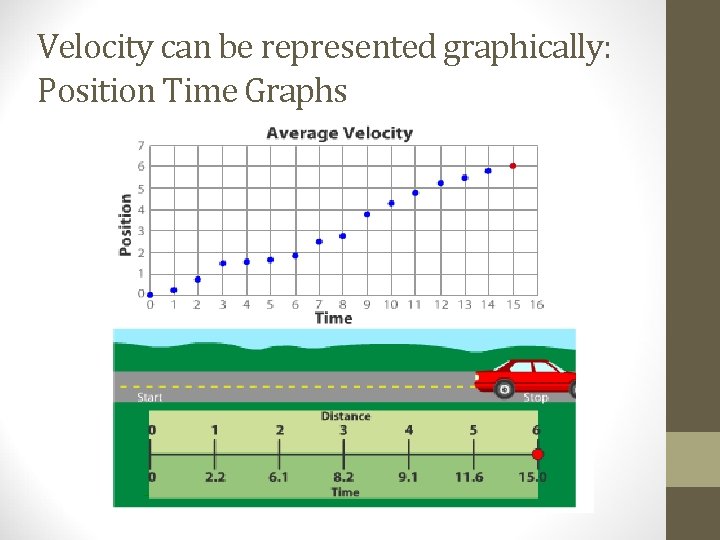
Velocity can be represented graphically: Position Time Graphs

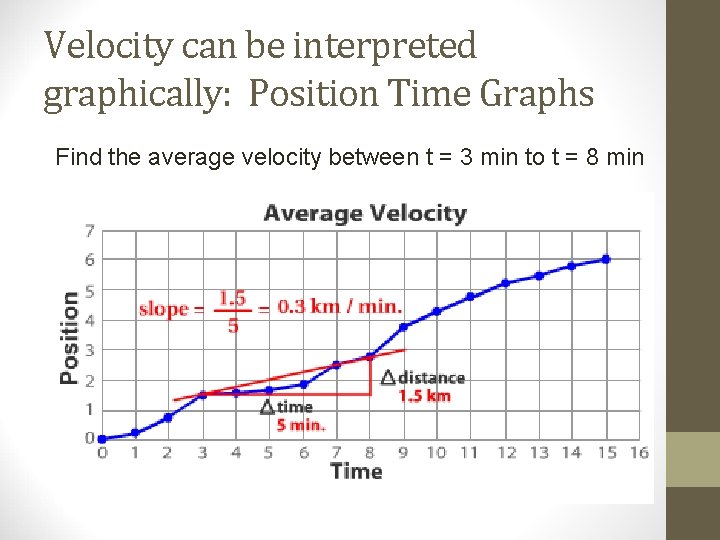
Velocity can be interpreted graphically: Position Time Graphs Find the average velocity between t = 3 min to t = 8 min

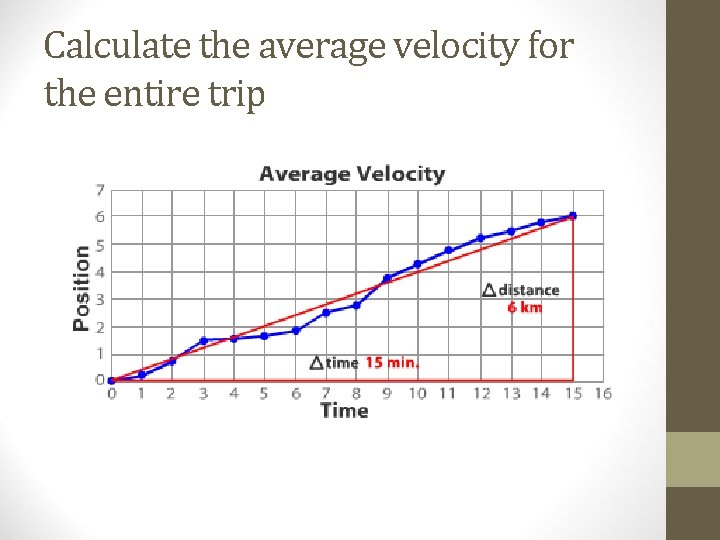
Calculate the average velocity for the entire trip

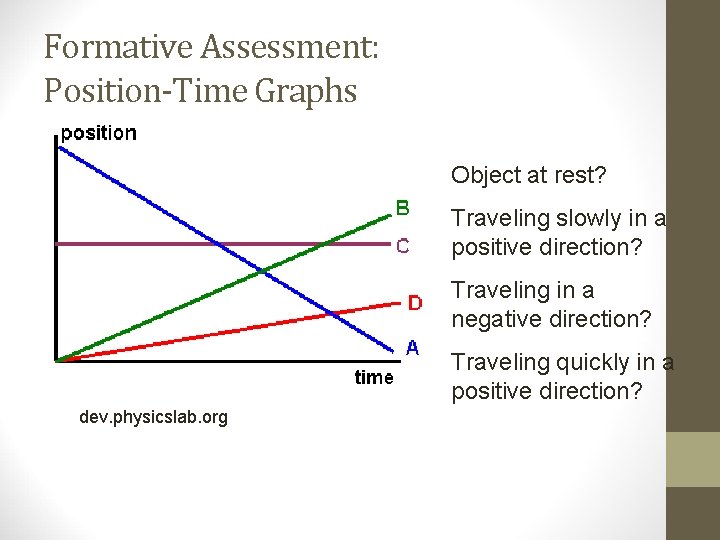
Formative Assessment: Position-Time Graphs Object at rest? Traveling slowly in a positive direction? Traveling in a negative direction? Traveling quickly in a positive direction? dev. physicslab. org

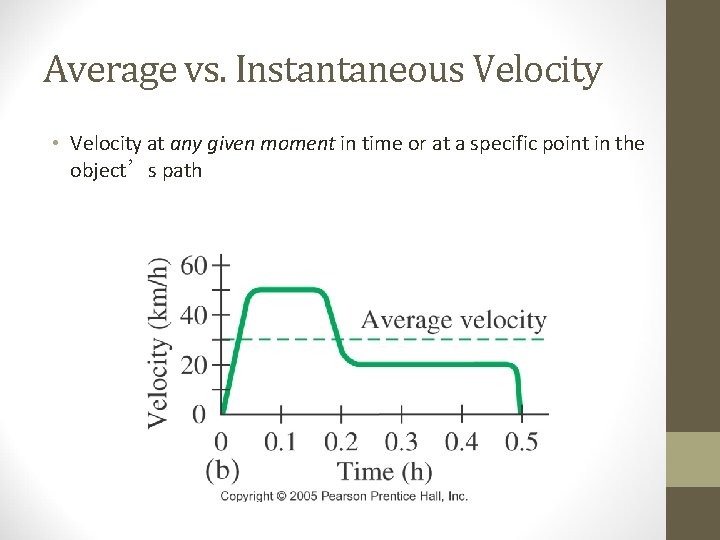
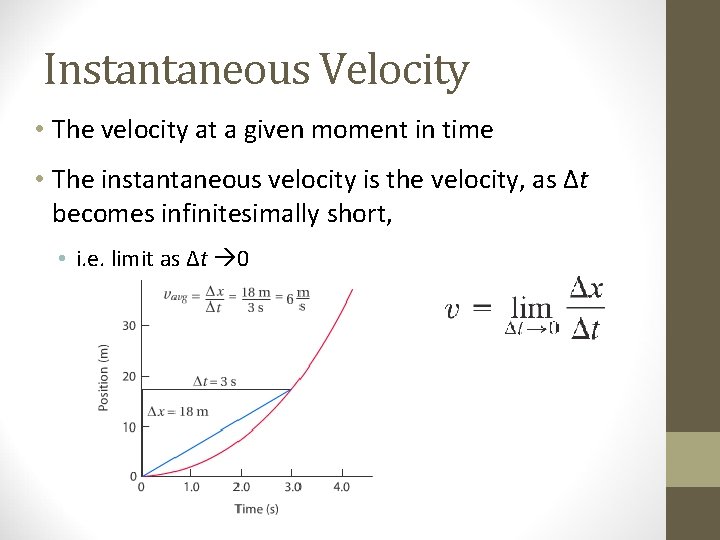
Average vs. Instantaneous Velocity • Velocity at any given moment in time or at a specific point in the object’s path

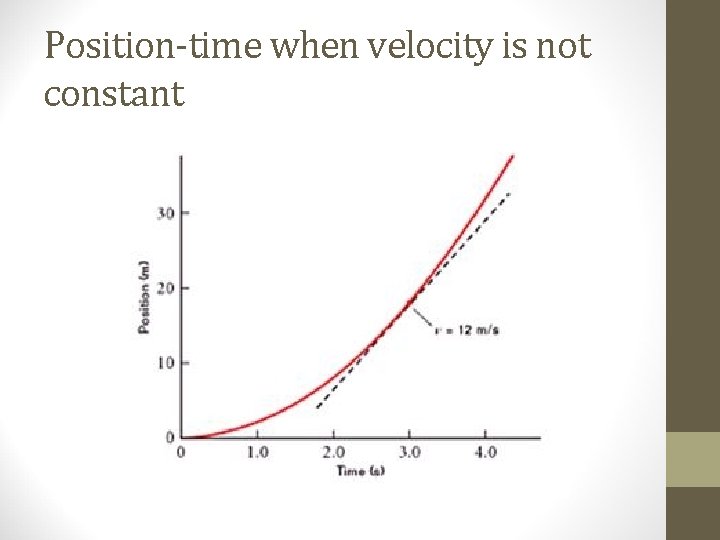
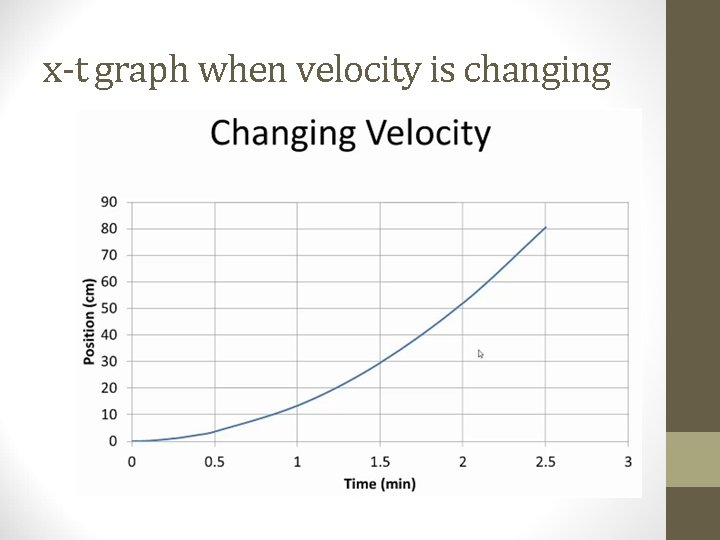
Position-time when velocity is not constant

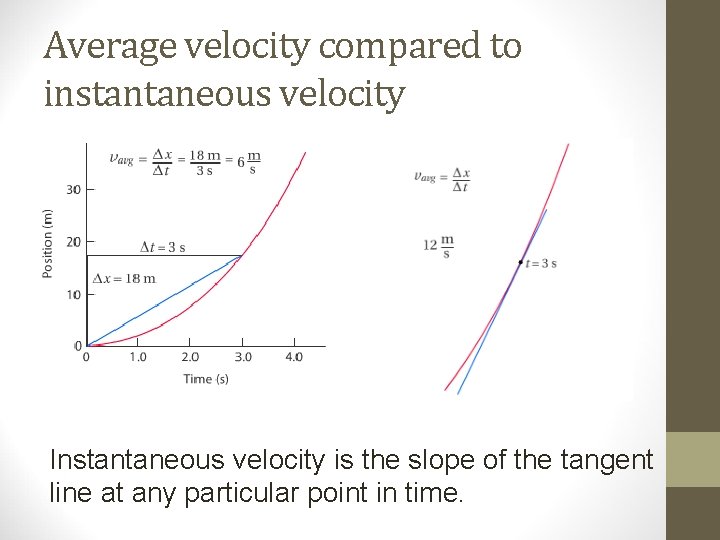
Average velocity compared to instantaneous velocity Instantaneous velocity is the slope of the tangent line at any particular point in time.

Instantaneous Velocity • The velocity at a given moment in time • The instantaneous velocity is the velocity, as Δt becomes infinitesimally short, • i. e. limit as Δt 0

2. 2 Acceleration

2. 2 Acceleration Learning Objectives • Describe motion in terms of changing velocity • Compare graphical representations of accelerated and nonaccelerated motions • Apply kinematic equations to calculate distance, time, or velocity under conditions of constant acceleration

x-t graph when velocity is changing

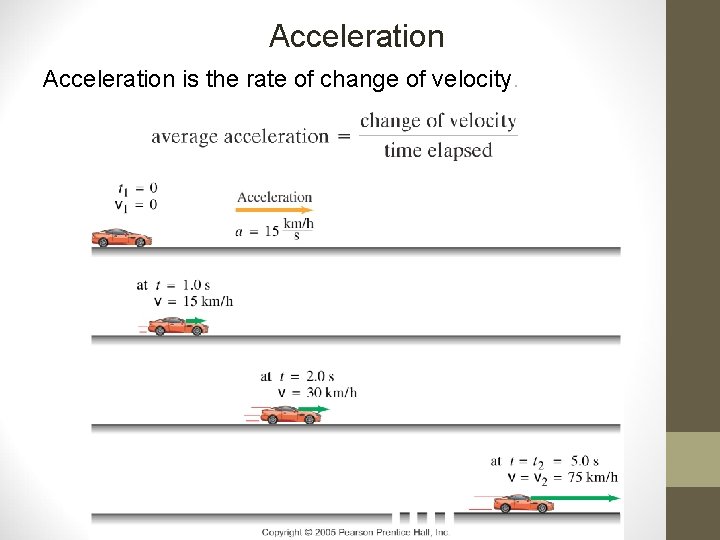
Acceleration is the rate of change of velocity.

Acceleration: Change in Velocity Acceleration is the rate of change of velocity a = ∆v/∆t a = (vf – vi) / (tf – ti) Since velocity is a vector quantity, velocity can change in magnitude or direction • Acceleration occurs whenever there is a change in magnitude or direction of movement. • •

Acceleration Because acceleration is a vector, it must have direction Here is an example of negative acceleration:

Customary Dimensions of Acceleration • a = ∆v/∆t • = m/s/s • = m/s 2 • Sample problems 2 B A bus traveling at 9. 0 m/s slows down with an average acceleration of -1. 8 m/s. How long does it take to come to a stop?

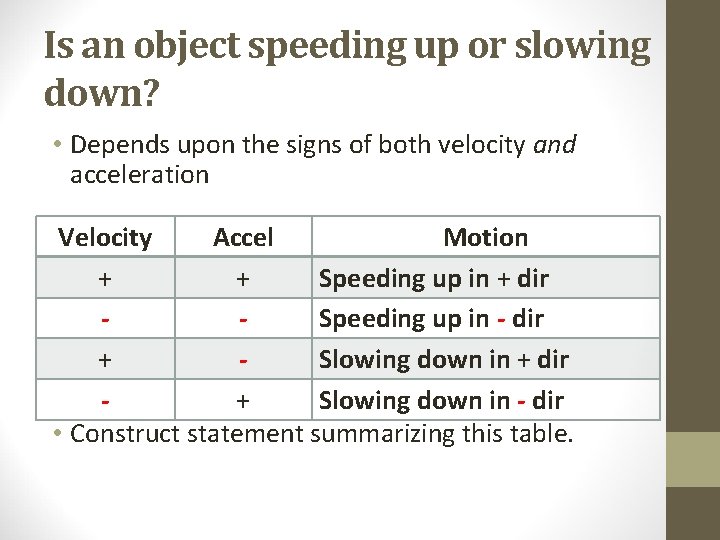
Negative Acceleration • Both velocity & acceleration can have (+) and (-) values • Negative acceleration does not always mean an object is slowing down

Is an object speeding up or slowing down? • Depends upon the signs of both velocity and acceleration Velocity Accel Motion + + Speeding up in + dir Speeding up in - dir + Slowing down in + dir + Slowing down in - dir • Construct statement summarizing this table.

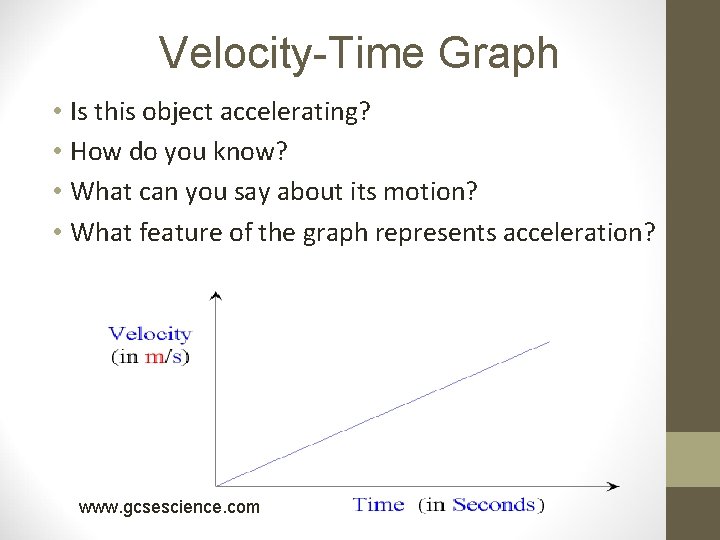
Velocity-Time Graphs • Is this object accelerating? • How do you know? • What can you say about its motion? www. gcsescience. com

Velocity-Time Graph • Is this object accelerating? • How do you know? • What can you say about its motion? • What feature of the graph represents acceleration? www. gcsescience. com

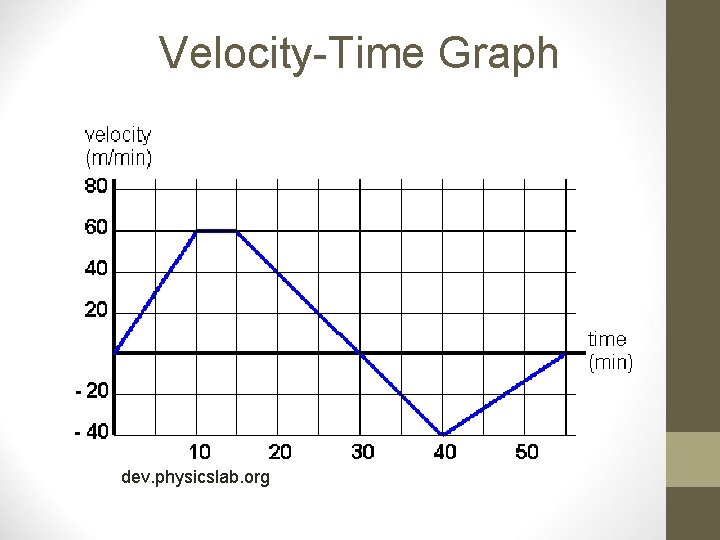
Velocity-Time Graph dev. physicslab. org

Displacement with Constant Acceleration (C)

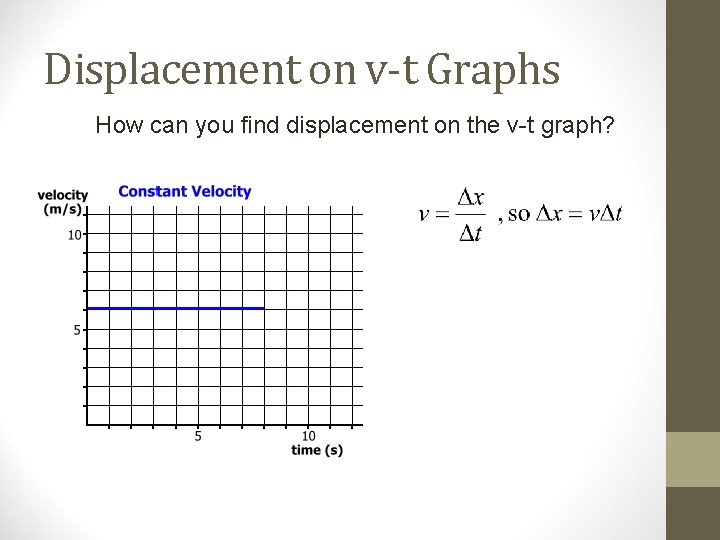
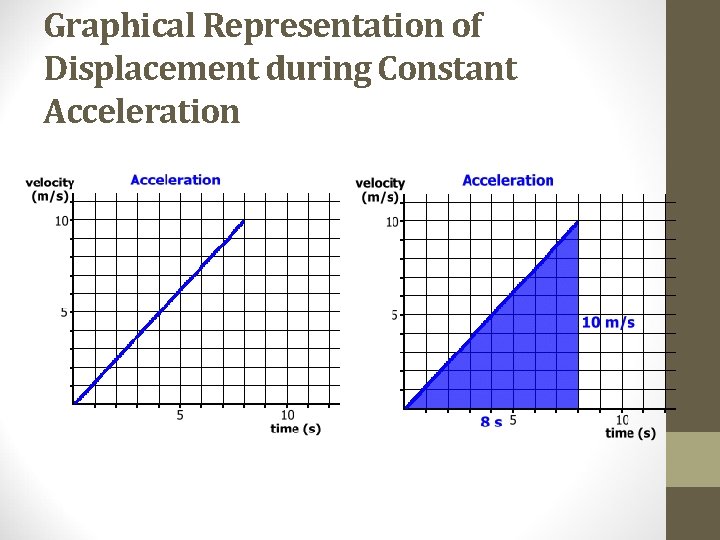
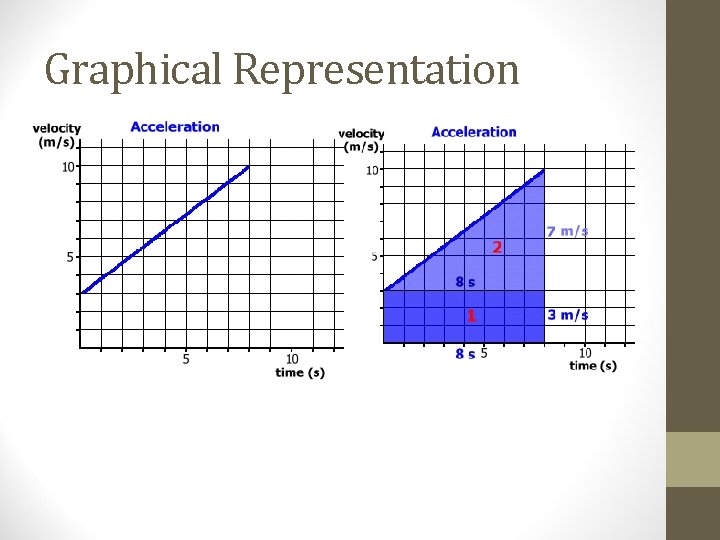
Displacement on v-t Graphs How can you find displacement on the v-t graph?

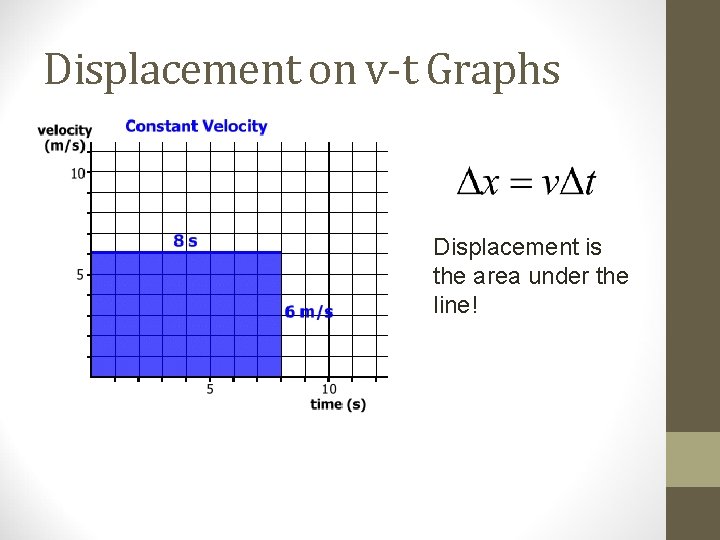
Displacement on v-t Graphs Displacement is the area under the line!

Graphical Representation of Displacement during Constant Acceleration

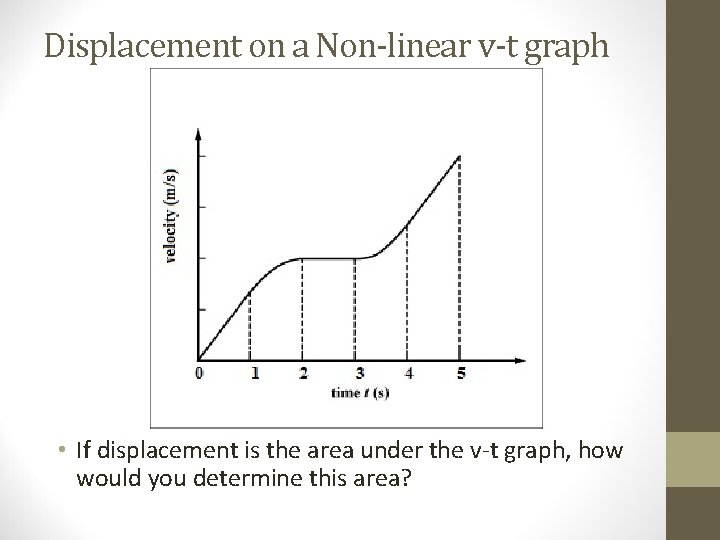
Displacement on a Non-linear v-t graph • If displacement is the area under the v-t graph, how would you determine this area?

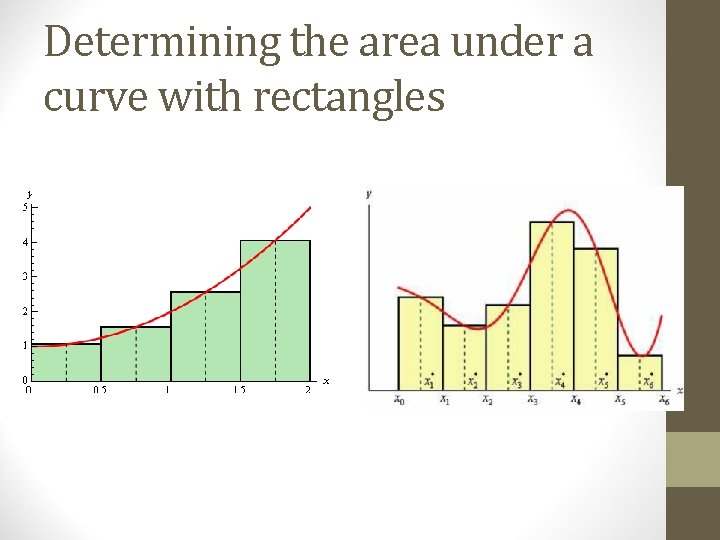
Determining the area under a curve with rectangles

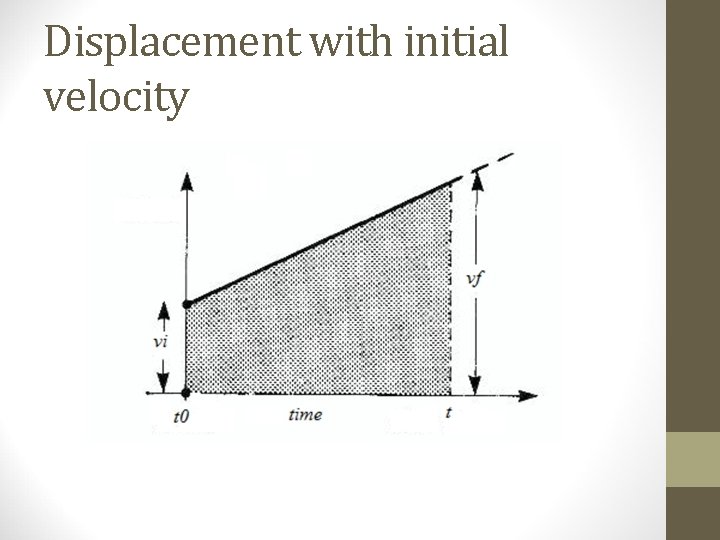
Displacement with initial velocity

Final velocity of an accelerating object

Displacement During Constant Acceleration (D)

Graphical Representation

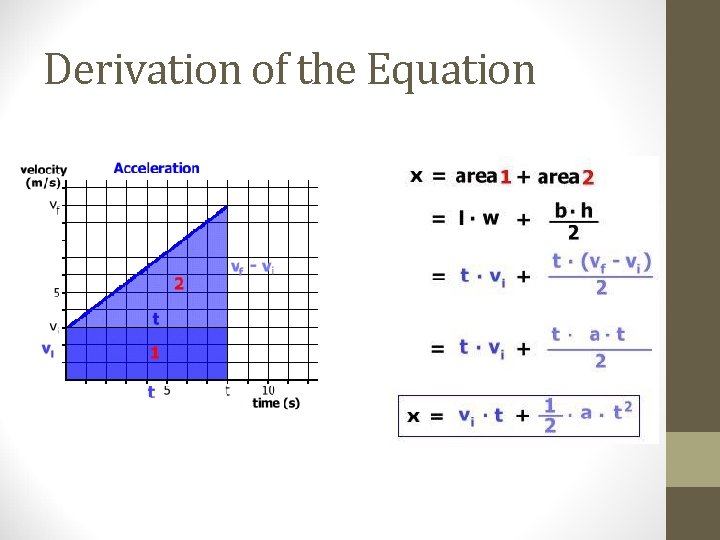
Derivation of the Equation

Final velocity after any displacement (E) A baby sitter pushes a stroller from rest, accelerating at 0. 500 m/s 2. Find the velocity after the stroller travels 4. 75 m. (p. 57) Identify the variables. Solve for the unknown. Substitute and solve.
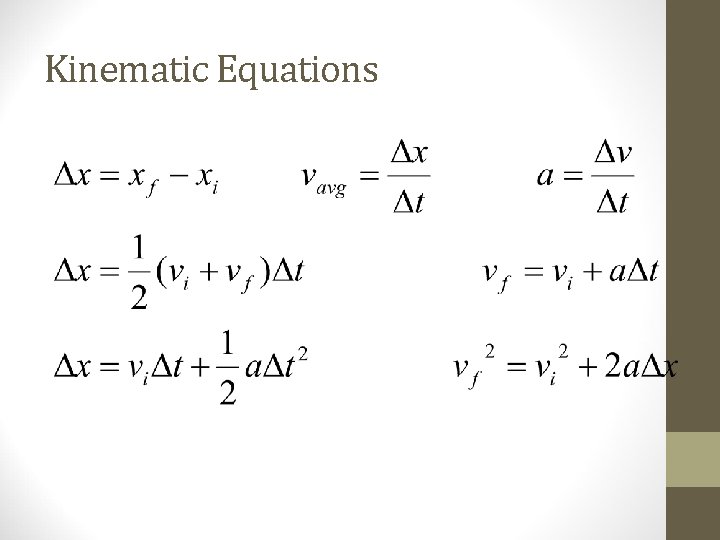
Kinematic Equations

2. 3 Falling Objects Objectives 1. Relate the motion of a freely falling body to motion with constant acceleration. 2. Calculate displacement, velocity, and time at various points in the motion of a freely falling object. 3. Compare the motions of different objects in free fall.

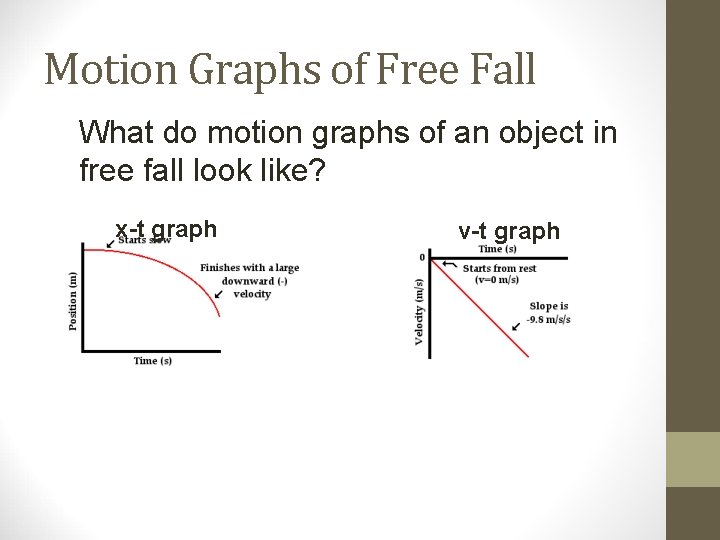
Motion Graphs of Free Fall What do motion graphs of an object in free fall look like?

Motion Graphs of Free Fall What do motion graphs of an object in free fall look like? x-t graph v-t graph

Do you think a heavier object falls faster than a lighter one? Why or why not? Yes because …. No, because ….

Free Fall • In the absence of air resistance, all objects fall to earth with a constant acceleration • The rate of fall is independent of mass • In a vacuum, heavy objects and light objects fall at the same rate. • The acceleration of a free-falling object is the acceleration of gravity, g • g = 9. 81 m/s 2 memorize this value!

Free Fall • Free fall is the motion of a body when only the force due to gravity is acting on the body. • The acceleration on an object in free fall is called the acceleration due to gravity, or free-fall acceleration. • Free-fall acceleration is denoted with by ag (generally) or g (on Earth’s surface).

Free Fall Acceleration • Free-fall acceleration is the same for all objects, regardless of mass. • This book will use the value g = 9. 81 m/s 2. • Free-fall acceleration on Earth’s surface is – 9. 81 m/s 2 at all points in the object’s motion. • Consider a ball thrown up into the air. – Moving upward: velocity is decreasing, acceleration is – 9. 81 m/s 2 – Top of path: velocity is zero, acceleration is – 9. 81 m/s 2 – Moving downward: velocity is increasing, acceleration is – 9. 81 m/s 2

Sample Problem • Falling Object • A player hits a volleyball so that it moves with an initial velocity of 6. 0 m/s straight upward. • If the volleyball starts from 2. 0 m above the floor, • how long will it be in the air before it strikes the floor?

Sample Problem, continued 1. Define Given: vi = +6. 0 m/s a = –g = – 9. 81 m/s 2 Δ y = – 2. 0 m Diagram: Place the origin at the Starting point of the ball (yi = 0 at ti = 0). Unknown: Δt = ?

2. Plan Choose an equation or situation: Both ∆t and vf are unknown. We can determine ∆t if we know vf Solve for vf then substitute & solve for ∆t 3. Calculate Rearrange the equation to isolate the unknowns: vf = - 8. 7 m/s Δt = 1. 50 s

Is there another way? • Is there another equation that would answer the question in a single step?

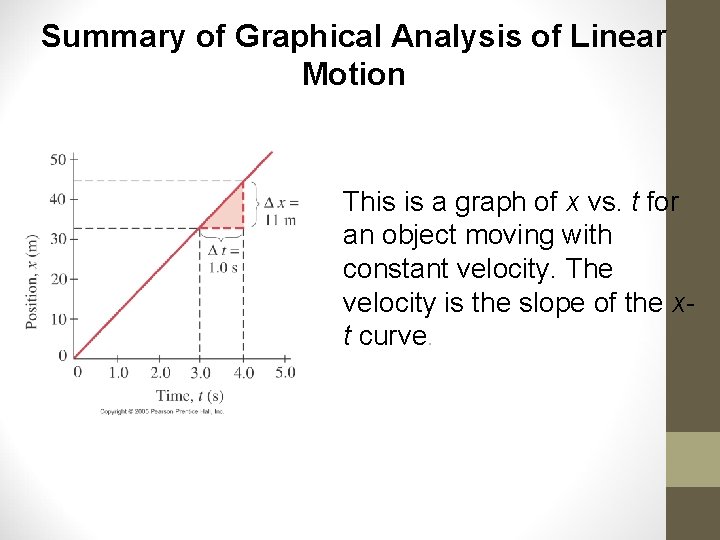
Summary of Graphical Analysis of Linear Motion This is a graph of x vs. t for an object moving with constant velocity. The velocity is the slope of the xt curve.

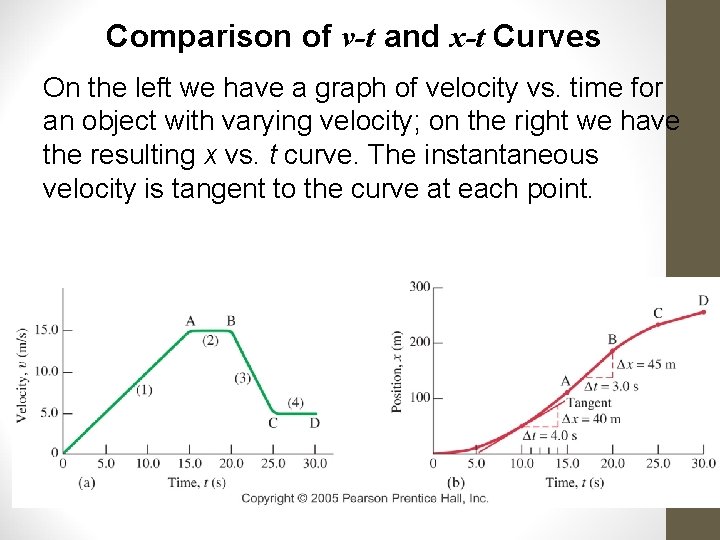
Comparison of v-t and x-t Curves On the left we have a graph of velocity vs. time for an object with varying velocity; on the right we have the resulting x vs. t curve. The instantaneous velocity is tangent to the curve at each point.

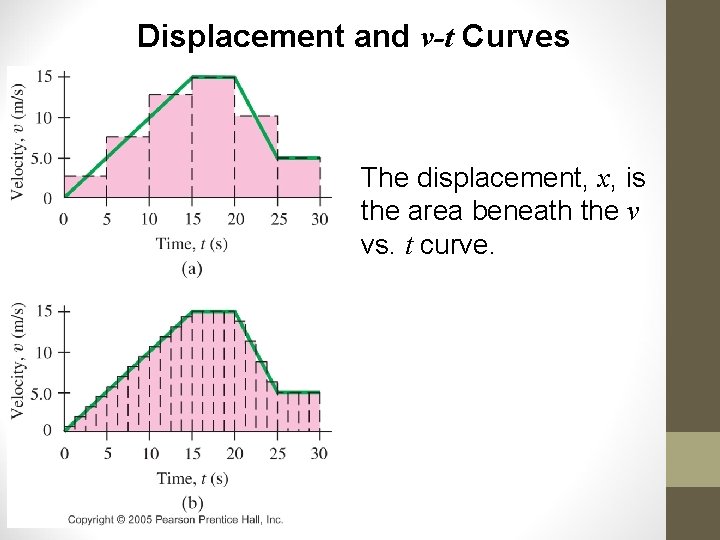
Displacement and v-t Curves The displacement, x, is the area beneath the v vs. t curve.

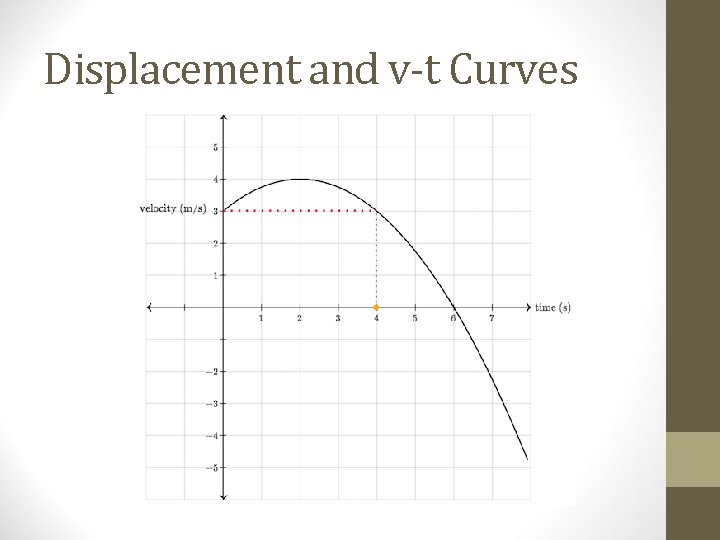
Displacement and v-t Curves
 Kinematics in one dimension
Kinematics in one dimension Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Motion in one dimension quiz
Motion in one dimension quiz Chapter 2 motion in one dimension answer key
Chapter 2 motion in one dimension answer key A man named bungkas climbed a palm tree
A man named bungkas climbed a palm tree Free fall motion in one dimension
Free fall motion in one dimension Motion in one dimension
Motion in one dimension Motion in one dimension
Motion in one dimension Mathematical techniques
Mathematical techniques Single displacement vs double displacement
Single displacement vs double displacement Dimension of displacement
Dimension of displacement Rectilinear kinematics: continuous motion
Rectilinear kinematics: continuous motion Example of continuous motion
Example of continuous motion Galileo trick kinematics
Galileo trick kinematics What is continuous motion in dynamics
What is continuous motion in dynamics Kinematic equations rearranged
Kinematic equations rearranged Kinematics of simple harmonic motion
Kinematics of simple harmonic motion Aplusphysics kinematics-free fall answers
Aplusphysics kinematics-free fall answers Kinematics: motion along a straight line
Kinematics: motion along a straight line Motion along a straight line definition
Motion along a straight line definition 1.n projectile motion part 2
1.n projectile motion part 2 Rectilinear motion with variable acceleration
Rectilinear motion with variable acceleration One dimensional kinematics problems
One dimensional kinematics problems Motion
Motion Angular displacement
Angular displacement Graphical representation of shm
Graphical representation of shm Determinant of gait
Determinant of gait Vectors in one dimension
Vectors in one dimension To describe a position in more than one dimension
To describe a position in more than one dimension Forces in one dimension vocabulary review
Forces in one dimension vocabulary review Chapter 4 forces in one dimension answer key
Chapter 4 forces in one dimension answer key What is collinear
What is collinear Time dimensions in research
Time dimensions in research One empire one god one emperor
One empire one god one emperor One one little dog run
One one little dog run One king one law one faith
One king one law one faith One god one empire one emperor
One god one empire one emperor Ford one plan
Ford one plan See one do one teach one
See one do one teach one One price policy
One price policy One face one voice one habit and two persons
One face one voice one habit and two persons Studiendekanat uni bonn
Studiendekanat uni bonn Asean tourism strategic plan
Asean tourism strategic plan One vision one identity one community
One vision one identity one community Type of range of motion
Type of range of motion Shm
Shm An object in motion stays in motion
An object in motion stays in motion Chapter 2 section 1 describing motion answer key
Chapter 2 section 1 describing motion answer key Describing and measuring motion
Describing and measuring motion Chapter 2 section 1 describing motion answer key
Chapter 2 section 1 describing motion answer key Chapter 1 lesson 2 describing motion answer key
Chapter 1 lesson 2 describing motion answer key Section 1 describing motion
Section 1 describing motion Tricycle kinematics
Tricycle kinematics What is kinematics
What is kinematics 2d motion equations
2d motion equations Rotational kinematics
Rotational kinematics Rotational motion equations
Rotational motion equations Plane kinematics of rigid bodies
Plane kinematics of rigid bodies Holonomic drive
Holonomic drive Laws of kinematics
Laws of kinematics Dr frost further kinematics
Dr frost further kinematics Kinematic equaitons
Kinematic equaitons