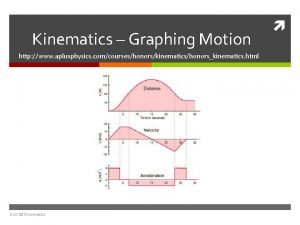
Motion in One Dimension Kinematics Distance vs Displacement










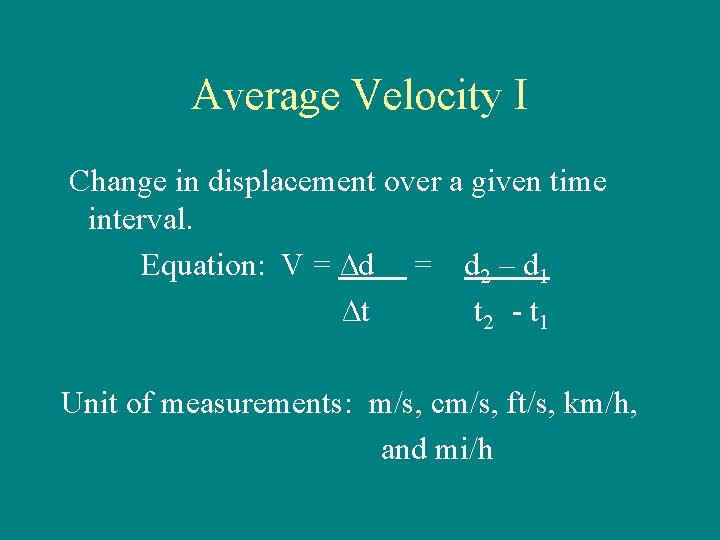









- Slides: 21

Motion in One Dimension Kinematics

Distance vs. Displacement • Distance – how far you’ve traveled Scalar quantity - 20 m • Displacement – shortest distance traveled from starting point to end point. Vector quantity – 20 m, 40 o, N of W

Instantaneous Position Where an object is located at one and only one time. • At 1. 0 s, object is at 3. 0 m • At 2. 0 s, object is at 6. 0 m Time (s) 1. 0 2. 0 Position (m) 3. 0 6. 0

Remember the example? Change the paces to meters (m). • Walk due west for 52 m, then walk 30. 0 o North of West for 42 m, and then walk due north for 25 m. • The total distance traveled was (52 + 42 + 25)m = 119 m The total displacement is 99 Paces, 28 o, N of W


Speed is how fast an object is moving. Scalar quantity = 30 km/h

Velocity is how fast an object is moving in a certain direction. Vector quantity = o 30 km/h, 45 , S of E

Direction of Velocity (+) Velocity is positive (+) if moving due east or due north. N E

Direction of Velocity (-) • Velocity is negative (-) is moving due west or due south. W S

Constant Velocity • Average velocity is the same for all time intervals. Time (s) 1. 0 Velocity (m/s) 30. 2. 0 30.

Instantaneous Velocity Speed and direction at one and only one time. At 1. 0 s, the instantaneous velocity is 35 m/s. At 2. 0 s, the instantaneous velocity is 55 m/s. Time (s) Velocity (m/s) 1. 0 35 2. 0 55
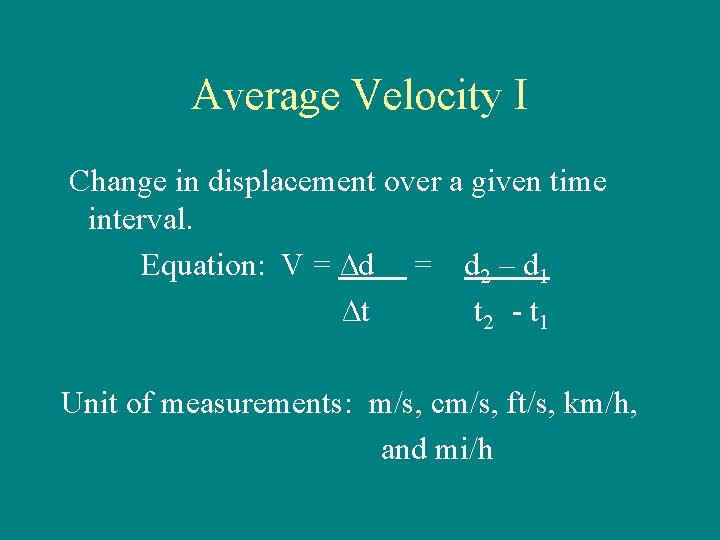
Average Velocity I Change in displacement over a given time interval. Equation: V = ∆d = d 2 – d 1 ∆t t 2 - t 1 Unit of measurements: m/s, cm/s, ft/s, km/h, and mi/h

Average Speed Total distance traveled over total time Equation: V = dt tt = d 1 + d 2 +. . t 1 + t 2 + …. . Units of Measurements: m/s, cm/s, ft/s, km/h, and mi/h

Conversions • Kilo = 1000 1 Km = 1000 m • 1 mi. = 1609 km • 1 h = 3600 s • Change 20. 0 m/s to Km/h 20. 0 m s x 1 Km x 3600 s 1000 m 1 h = 72 km/h

Example 1 • A person walks 13 km in 2. 0 h. What is the person’s average velocity in km/h and m/s? V = ∆d = d 2 – d 1 = 13 km ∆t t 2 - t 1 2. 0 h 6. 5 Km h = 6. 5 km/h x 1000 m x 1 h = 1. 8 m/s 1 Km 3600 s

Example 2 A car traveled 2. 0 mi. in 0. 2 h, 5. 0 mi in 0. 6 h and 15. 0 mi in 1. 0 h. What was the average speed of the car? V = dt = d 1 + d 2 + d 3 tt t 1 + t 2 + t 3 = 2. 0 mi + 5. 0 mi + 15. 0 mi = 12 mi/h = 10 mi/h 0. 2 h + 0. 6 h + 1. 0 h

Example 3 A car traveled 2. 0 h at a speed of 50 mi/h and 4. 0 h at 75 mi/h. Calculate the average speed. V = (2. 0 h x 50. mi/h) + (4. 0 h x 75 mi/h) 2. 0 h + 4. 0 h V = 67 mi/h

Example 4 • A toy train starts at 0 m and runs around the 1. 0 m track in 30 s. train stops at the starting point. What was its average speed? V = 1. 0 m/30 s = 0. 03 m/s What was its average velocity? V = 0 m/s. It stopped at its starting point. The change in displacement is 0.

Average Acceleration • Change in velocity over a period of time. a = ∆V = V 2 – V 1 ∆t t 2 - t 1 Units of measurements: m/s 2, cm/s 2, ft/s 2 km/h 2, and mi/h 2

Direction of Acceleration • Positive if the change in velocity is positive. ∆V = 40 m/s – 20 m/s = + 20 m/s Acceleration is increasing. • Negative if the change in velocity is negative. ∆V = 20 m/s – 40 m/s = -20 m/s Acceleration is decreasing. (decelerating)

Acceleration Example An Indy-500 race car’s velocity increases from +4. 0 m/s to +36 m/s over a 4. 0 s period. What is its average acceleration? V 1 = +4. 0 m/s V 2 = +36. 0 m/s ∆t = 4. 0 s a = ∆V = +36. 0 m/s – +4. 0 m/s = 8. 0 m/s 2 ∆t 4. 0 s
 Dot diagram motion
Dot diagram motion Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Describing motion kinematics in one dimension
Describing motion kinematics in one dimension How is distance different from displacement
How is distance different from displacement Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Motion in one dimension quiz
Motion in one dimension quiz Vf-vo
Vf-vo Bungkas tree
Bungkas tree Free fall motion in one dimension
Free fall motion in one dimension Motion in one dimension
Motion in one dimension 2d motion equations
2d motion equations Mathematical techniques
Mathematical techniques Single displacement vs double displacement
Single displacement vs double displacement Dimension of displacement
Dimension of displacement Rectilinear kinematics: continuous motion
Rectilinear kinematics: continuous motion Rectilinear kinematics
Rectilinear kinematics Aplusphysics ucm gravity answer key
Aplusphysics ucm gravity answer key Rectilinear kinematics continuous motion
Rectilinear kinematics continuous motion Rearranging kinematic equations
Rearranging kinematic equations Kinematics of simple harmonic motion
Kinematics of simple harmonic motion Aplusphysics kinematics-defining motion answers
Aplusphysics kinematics-defining motion answers Graphical integration in motion analysis
Graphical integration in motion analysis