Kapitel 17 Dynamische Modelle Konzepte Hackl Einfhrung in

Kapitel 17 Dynamische Modelle: Konzepte Hackl, Einführung in die Ökonometrie (17)

Argumente für dynamische Modelle (a) Ökonomische Aktivitäten sind oft durch die Vergangenheit bestimmt; z. B. : Konsum von Energie hängt von Investitionen der Vergangenheit in energieverbrauchende Anlagen und Geräte ab (b) Akteure der ökonomischen Prozesse reagieren oft verzögert; z. B. wegen der Dauer von Entscheidungs- und Beschaffungsprozessen (c) Erwartungen: z. B. : Konsum hängt nicht nur vom aktuellen Einkommen, auch von der Einkommenserwartung ab; Modellierung der Erwartung basiert auf Entwicklung in der Vergangenheit Hackl, Einführung in die Ökonometrie (17) 2

Elemente dynamischer Modelle 1. 2. 3. Lagstrukturen, d. s. Linearkombinationen aktueller und vergangener Werte der Variablen Modelle für Erwartungen: basieren auf Lagstrukturen; z. B. adaptive Erwartung, partielle Anpassung Das ADL-Modell: einfaches, aber allgemein anwendbares Modell, das aus einem autoregressiven Teil und aus einer endlichen Lagstruktur der unabhängigen Variablen besteht Hackl, Einführung in die Ökonometrie (17) 3

Beispiel: Nachfragefunktionen n n Nachfrage nach dauerhaften Konsumgütern: Die Nachfrage Q hängt vom Preis P und vom Einkommen Y der aktuellen und zweier vergangener Perioden ab: Qt = a + b 0 Yt + b 1 Yt-1 + b 2 Yt-2 + g Pt + ut Nachfrage nach Energie: Sie wird beschrieben durch Qt = a + b. Pt + g Kt + ut mit P: Preis für Energie, K: energie-relevanter Kapitalbestand Kt = q 0 + q 1 Pt-1 + q 2 Pt-2 + … + d. Yt + vt mit Y: Einkommen; Einsetzen gibt Qt = a 0 + a 1 Yt + b 0 Pt + b 1 Pt-1 + b 2 Pt-1 + … + et mit et = ut + g vt, a 0 = a + gd, b 0 = b, und bi = gqi, i = 1, 2, … Hackl, Einführung in die Ökonometrie (17) 4

Das DL(s)-Modell Die allgemeine Form eines dynamischen Modells mit verzögerter Wirkung einer exogenen Variablen kann geschrieben werden als Yt = a + b 0 Xt + b 1 Xt-1 + … + bs. Xt-s + ut s: maximales Lag oder Ordnung der Lagstruktur; kann unbeschränkt sein Endliche Lagstruktur: Ordnung s hat endlichen Wert Themen zu Lagstrukturen n das Schätzen der Modellparameter n die Interpretation der Koeffizienten Hackl, Einführung in die Ökonometrie (17) 5

Beispiel: Konsumfunktion Datensatz Dat. S 04: Konsum und Einkommen für Österreich (1976: 1 bis 1995: 2) In logarithmierten Differenzen: (a) Ĉ = 0. 009 + 0. 621 Y mit t(Y) = 2. 288, R 2 = 0. 335 (b) Ĉ = 0. 006 + 0. 504 Y – 0. 026 Y-1 + 0. 274 Y-2 mit t(Y) = 3. 79, t(Y-1) = – 0. 18, t(Y-2) = 2. 11, R 2 = 0. 370 Effekt des Einkommens auf Konsum? n Kurzfristiger Effekt: Wirkung in der aktuellen Periode (DC = 0. 504 bei DY = 1) n Gesamteffekt: Summe der Koeffizienten (DC = 0. 752 bei DY = 1) Hackl, Einführung in die Ökonometrie (17) 6

Multiplikatoren Beschreiben den Effekt von Änderungen in der/den erklärenden Variablen auf die abhängige Variable Yt = a + b 0 Xt + b 1 Xt-1 + … + bs. Xt-s + ut n n Kurzfristiger Multiplikator (short run oder impact multiplier): Effekt einer Änderung von X um DX = 1 auf Y in der gleichen Periode (DY = b 0) Langfristige Multiplikator (long run multiplier): der über alle Zukunft kumulierte Effekt von DX = 1 (DY = b 0 + … + bs) Hackl, Einführung in die Ökonometrie (17) 7

Gleichgewichts-Effekt Wenn nach einer Änderung DX innerhalb einer endlichen Zeit ein Gleichgewichts-Zustand eintritt: langfristiger Multiplikator wird als Gleichgewichts-Effekt (equilibrium multiplier) bezeichnet n Im Modell Yt = a + b 0 Xt + b 1 Xt-1 + … + bs. Xt-s + ut wird in s Perioden der Gleichgewichts-Zustand erreicht n Bei einer unendlichen Lagstruktur wird die Anpassung nie vollendet Hackl, Einführung in die Ökonometrie (17) 8

Durchschnittliche Lag-Zeit Anteil der Anpassung am kumulierten Effekt: Charakterisierung des Anpassungsprozesses n Anteil am Ende der aktuellen Periode: b 0/(b 0 + … + bs) = w 0 n Anteil am Ende der Periode t +1: (b 0 + b 1)/(b 0 + … + bs) = w 0 + w 1 n usw. mit Gewichten wi = bi/(b 0 + … + bs) , i = 0, …, s n n Durchschnittliche Lag-Zeit: Sis i wi Mediane Lag-Zeit: Dauer bis zur Anpassung von 50%; minimales s* mit w 0 + … ws* ≥ 0. 5 Hackl, Einführung in die Ökonometrie (17) 9

Konsumfunktion, Forts. Ĉ = 0. 006 + 0. 504 Y – 0. 026 Y-1 + 0. 274 Y-2 Effekt des Einkommens auf Konsum? Für DY = 1 ergeben sich: n Kurzfristiger Effekt: 0. 504 n Gesamteffekt: 0. 504 – 0. 026 + 0. 274 = 0. 752 n Gleichgewichts-Effekt ist gleich dem Gesamteffekt: 0. 752 n Mediane Lag-Zeit: die kumulierten Summen der Gewichte betragen 0. 671, 0. 636, 1. 000; 50% der Anpassung werden überschritten in s* = 0 n Durchschnittliche Lag-Zeit: 0. 694 Quartale, d. s. etwa 2. 3 Monate Hackl, Einführung in die Ökonometrie (17) 10

Lagstrukturen: Schätz-Probleme bei OLS-Anpassung einer Lagstruktur (Ordnung s): n „Verlust von Beobachtungen“: es stehen nur n - s Beobachtungen zur Verfügung; unendliche Lagstruktur! n Multikollinearität n Ordnung s (meist) nicht bekannt Konsequenzen der ersten beiden Probleme: n große Standardfehler der geschätzten Koeffizienten n geringe Mächtigkeit der Tests zu den Koeffizienten Themen: n Verfahren zur Wahl der Ordnung s n Modellierung von Lagstrukturen, z. B. als polynomiale Struktur Hackl, Einführung in die Ökonometrie (17) 11

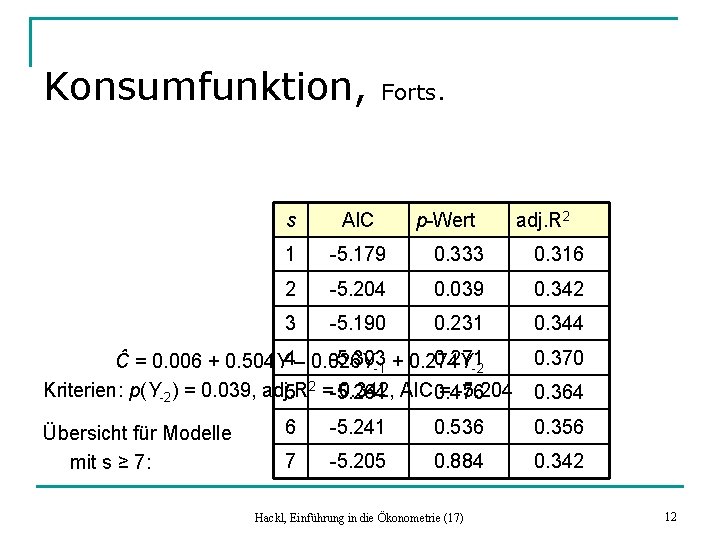
Konsumfunktion, Forts. s AIC p-Wert 1 -5. 179 0. 333 0. 316 2 -5. 204 0. 039 0. 342 3 -5. 190 0. 231 0. 344 -5. 303 0. 271 Ĉ = 0. 006 + 0. 504 Y 4– 0. 026 Y -1 + 0. 274 Y-2 Kriterien: p(Y-2) = 0. 039, adj. R 0. 342, AIC 0. 476 = -5. 204 5 2 =-5. 264 Übersicht für Modelle mit s ≥ 7: adj. R 2 0. 370 0. 364 6 -5. 241 0. 536 0. 356 7 -5. 205 0. 884 0. 342 Hackl, Einführung in die Ökonometrie (17) 12

Verfahren zur Wahl von s Auswahl unter Modellen mit s = 0, 1, …, S durch Verwendung des AIC (oder eines anderen Informationskriteriums) 1. 2. 3. 4. Wahl des maximalen Lags S Schätzen der Koeffizienten aller möglicher Modelle für s = 1, …, S Bestimmen des AIC(s), des adjustierten Bestimmtheitsmaßes oder eines anderen Kriteriums Wahl der Ordnung als jenes s, für das AIC(s) minimal ist, das adjustierte Bestimmtheitsmaß maximal ist, etc. Hackl, Einführung in die Ökonometrie (17) 13

Polynomiale Lagstruktur auch Almon‘sches Lag genannt DL(s)-Modell Yt = a + b 0 Xt + b 1 Xt-1 + … + bs. Xt-s + ut = a + B(L)Xt + ut mit B(L) = b 0 + b 1 L + … + bs. Ls, L: Lagoperator (LXt = Xt-1, Lr. Xt = Xt-r, L 0 Xt = Xt) Polynomiales Lag: bi, i = 1, …, s, ist ein Polynom der Ordnung r : bi = g 0 + g 1 i + … + gri r Mit r < s sind weniger Koeffizienten zu schätzen als im ursprünglichen Modell Hackl, Einführung in die Ökonometrie (17) 14

Beispiel: s=3, r=2 Diese Spezifikation liefert b 0 = g 0 b 1 = g 0 + g 1 + g 2 b 2 = g 0 + 2 g 1 + 4 g 2 b 3 = g 0 + 3 g 1 + 9 g 2 oder b = Tg mit der 3 x 4 -Matrix T Einsetzen liefert Yt = g 0 (Xt + … + Xt-3) + g 1 (Xt-1 + … + 3 Xt-3) + g 2 (Xt-1 + … + 9 Xt-3) + ut oder y = XTg + u = Wg + u; die erste Spalte von W enthält die Summen Xt + … + Xt-3, etc. Aus den Schätzern ci (für die gi) ergeben sich die bi entsprechend obigen Gleichungen Hackl, Einführung in die Ökonometrie (17) 15

Konsumfunktion, Forts. Ĉ = 0. 005 + 0. 539 Y – 0. 065 Y-1 + 0. 168 Y-2 + 0. 158 Y-3 Kriterien: adj. R 2 = 0. 344, AIC = -5. 190 Ĉ = 0. 005 + 0. 097 pdl 1(Y, 3, 2) – 0. 239 pdl 2(Y, 3, 2) + 0. 149 pdl 3(Y, 3, 2) Kriterien: adj. R 2 = 0. 335, AIC = -5. 190 Koeffizienten und in Klammer ihre t-Statistiken: b 0 = 0. 484 (3. 72) b 1 = 0. 097 (1. 04) b 2 = 0. 006 (0. 07) b 3 = 0. 213 (1. 70) oder Ĉ = 0. 005 + 0. 484 Y + 0. 097 Y-1 + 0. 006 Y-2 + 0. 213 Y-3 Hackl, Einführung in die Ökonometrie (17) 16

Koyck‘sche Lagstruktur Spezifiziert die Koeffizienten des DL(s)-Modells Yt = a + b 0 Xt + b 1 Xt-1 + … + bs. Xt-s + … + ut als unendliche, geometrische Folge (geometrische Lagstruktur): bi = b(1 -l)li Für 0 < l < 1 ergibt die Summe aller bi den Wert b! Beiträge zu DY bei einer Änderung von DX = 1: b(1 -l) in t (kurzfristiger Multiplikator), b(1 -l)l in t+1, etc; Beiträge werden je Periode um Faktor l kleiner; Gleichgewichts-Effekt: b 0. 1 0. 3 0. 5 0. 7 l durchschnittliche Lag-Zeit: l/(1 -l) 0. 10 0. 43 1. 00 2. 33 Stabilitätsbedingung: Die Bedingung 0 < l < 1 nennt man Stabilitätsbedingung: l ≥ 1 bedeutet explosiv wachsende bi bzw. explosiv wachsende Beiträge zu DY bei einer Änderung von DX Hackl, Einführung in die Ökonometrie (17) 17

Koyck‘sche Lagstruktur, Forts. DL (distributed lag)- oder MA (moving average)-Form des Modells Yt = a + b(1 -l) Sili. Xt-i + ut AR (autoregressive)-Form Yt = a(1 -l) + l. Yt-1 + b(1 -l) Xt + vt mit vt = ut – lut-1 Koyck-Transformation: Umformung der DL-Form in die AR-Form n durch Subtrahieren der l-fachen Gleichung für t-1 Hackl, Einführung in die Ökonometrie (17) 18

Konsumfunktion, Forts. Modell mit geringstem AIC: Ĉ = 0. 003 + 0. 595 Y – 0. 016 Y-1 + 0. 107 Y-2 + 0. 003 Y-3 + 0. 148 Y-3 Kriterien: adj. R 2 = 0. 370, AIC = -5. 303, DW = 1. 41 Koyck‘s Lag in AR-Form Ĉ = 0. 004 + 0. 286 C-1 + 0. 556 Y Kriterien: adj. R 2 = 0. 388, AIC = -5. 290, DW = 1. 91 Hackl, Einführung in die Ökonometrie (17) 19

Schätzprobleme Probleme beim Schätzen von l und b: n DL-Form: 1. Historische Werte X 0, X-1, X-2, … sind unbekannt! Näherungsweise äquivalentes Modell ist Yt = b(1 -l)(Xt + l. Xt-1 + … + lt-1 X 1 + b*lt + ut mit b* = b(1 -l)(X 0 + l. X-1 + … ) als drittem Parameter 2. Nichtlineares Schätzproblem! n AR-Form: 1. Nichtlineares Schätzproblem! 2. Verzögerte, endogene Variable als Regressor 3. Korrelierte Störgrößen Hackl, Einführung in die Ökonometrie (17) 20

Modelle in Erwartungen spielen in ökonomischen Prozessen wichtige Rolle Beispiele: Ø Konsum hängt nicht nur vom aktuellen Einkommen, sondern auch von der Erwartung künftiger Einkommen ab Ø Investitionen hängen von erwarteten Gewinnen ab Ø Zinsen hängen von der Einschätzung der Entwicklung des Kapitalmarktes ab Ø etc. Erwartungen sind n nicht beobachtbar n unter Annahmen über den Mechanismus der Erwartungsbildung modellierbar Hackl, Einführung in die Ökonometrie (17) 21

Modelle für Erwartungen In der Theorie sind folgende Modelle gebräuchlich n Naives Modell der Erwartung: Der (für die nächste Periode) erwartete Wert ist gleich dem aktuellen Wert n Modell der adaptiven Erwartung n Modell der partiellen Anpassung Letztere beiden Modelle basieren auf der Koyck‘schen Lagstruktur Hackl, Einführung in die Ökonometrie (17) 22

Modell der adaptiven Erwartung Beschreibt den aktuellen Wert Yt als Funktion des in der kommenden Periode erwarteten Wertes Xet+1 Yt = a + b. Xet+1 + ut Beispiel: Investitionen (Y) sind Funktion des erwarteten Gewinns Xet+1 Modelle für Xet+1: n Naives Modell: Xet+1 = Xt n Realistischer ist eine gewichtete Summe der in der Vergangenheit realisierten Gewinne Xet+1 = b 0 Xt + b 1 Xt-1 + … n Vorschlag von Cagan (1956): geometrisch abnehmende Gewichte bi mit 0 < l < 1 bi = (1 -l)li Hackl, Einführung in die Ökonometrie (17) 23

Adaptive Erwartung, Forts. Aus Xet+1 = b 0 Xt + b 1 Xt-1 + … mit bi = (1 -l)li ergibt sich mittels Koyck. Transformation Xet+1 = l Xet + (1 - l) Xt oder Xet+1 - Xet = (1 - l)(Xt - Xet) Interpretation: Änderung der Erwartung zwischen t und t+1 ist proportional dem „Fehler“ in der Erwartung, d. i. die Abweichung zwischen der aktuellen Erwartung und dem tatsächlich realisierten Wert Ausmaß der Änderung (Anpassung): 100(1 - l)% des „Fehlers“ l: Anpassungs-Parameter Hackl, Einführung in die Ökonometrie (17) 24

Adaptive Erwartung, Forts. Modell der adaptiven Erwartung (adaptive expectations model) Yt = a(1 – l) + l. Yt-1 + b(1 – l)Xt + vt mit vt = ut – lut-1 Ist die AR-Form zur DL-Form Yt = a + b(1 – l)Xt + b(1 – l)l. Xt-1 + … + ut Beispiel: Investitionen (I) sind Funktion des erwarteten Gewinns Pet+1 und des Zinssatzes (r) It = a + b. Pet+1 + grt + ut Modell für erwarteten Gewinn unterstellt adaptive Erwartung Pet+1 = Pet + (1 – l)Pt mit Anpassungs-Parameter l (0 < l < 1); AR-Form It = a(1 – l) + l. It-1 + b(1 – l)Pt + grt – lgrt-1 + vt der Investitionsfunktion mit vt = ut – lut-1 Hackl, Einführung in die Ökonometrie (17) 25

Konsumfunktion, Forts. Konsum als Funktion des erwarteten Einkommens: Ct = a + b. Yet+1 + ut mit erwartetem Einkommen aus adaptiver Erwartung Yet+1 = Yet + (1 – l)Yt Einsetzen liefert die AR-Form Ct = a(1 – l) + l. Ct-1 + b(1 – l)Yt + vt mit vt = ut – lut-1 Angepasstes Modell: Ĉ = 0. 004 + 0. 286 C-1 + 0. 556 Y Kriterien: adj. R 2 = 0. 388, AIC = -5. 29, DW = 1. 91 Hackl, Einführung in die Ökonometrie (17) 26

Modell der partiellen Anpassung Beschreibt den Prozess der Anpassung einer Größe an einen gewünschten Wert Beispiel: Der gewünschte (geplante) Lagerstand Kp als Funktion des Erlöses S Kpt = a + b. St + ut tatsächlicher Lagerstand der Vorperiode weicht vom gewünschten Lagerstand um Kpt – Kt-1 ab Strategie: Anpassung von Kt an Kpt um 100 d % der Abweichung Kpt – Kt-1: Kt – Kt-1 = d(Kpt – Kt-1) d: Anpassungs-Parameter (0 < d < 1) Hackl, Einführung in die Ökonometrie (17) 27

Partielle Anpassung, Forts. Modell der partiellen Anpassung (partial adjustment model): Beschreibt das Verhalten von Ypt als Funktion eines Regressors X Ypt = a + b. Xt + ut Partielles Anpassen des realisierten Y nach Yt – Yt-1 = d(Ypt – Yt-1) d: Anpassungs-Parameter (0 < d < 1) Realisiertes Y als gewichtetes Mittel zwischen geplantem Yp und realisiertem Y Yt = d. Ypt + (1 – d)Yt-1 AR-Form des Modells der partiellen Anpassung Yt = ad + (1 – d)Yt-1 + bd. Xt + dut Hackl, Einführung in die Ökonometrie (17) 28

AR-Formen Die AR-Formen n der Koyck‘schen Lagstruktur n des Modells der adaptiven Erwartung n des Modells der partiellen Anpassung haben die gleiche Form sie unterscheiden sich in den Störgrößen: n diese sind Weißes Rauschen im Fall des Modells der partiellen Anpassung n sie sind korreliert in den beiden anderen Fällen Hackl, Einführung in die Ökonometrie (17) 29

Das ADL-Modell Die allgemeine Form, das ADL(p, s)-Modell, lautet Yt = a + j 1 Yt-1 + … + jp. Yt-p + b 0 Xt + … + bs. Xt-s + ut es besteht aus n einer Lagstruktur der Ordnung p der abhängigen Variablen n einer Lagstruktur der Ordnung s der erklärenden Variablen Darstellung mittels Lag-Operator L: A(L)Yt = a + b(L)Xt + ut mit A(L) = 1 – j 1 L – … – jp. Lp und b(L) = b 0 + b 1 L + … + bs. Ls Hackl, Einführung in die Ökonometrie (17) 30

ADL(1, 1)-Modell: Yt = a + j. Yt-1 + b 0 Xt + b 1 Xt-1 + ut Spezialfälle sind: n Statisches Modell: j = b 1 = 0 n DL(1)-Modell: j = 0 n AR(1)-Modell: b 0 = b 1 = 0 Verallgemeinerungen ergeben sich, wenn korrelierte Störgrößen zugelassen werden Die meisten dynamischen Modelle gehören zur Klasse der ADL(1, 1)Modelle Hackl, Einführung in die Ökonometrie (17) 31

ADL(1, 1)-Modell: Beispiele n n AR-Form [Yt = l. Yt-1 + b(1 – l)Xt + vt] des Modells mit Koyck‘scher Lagstruktur, d. i. Yt = b(1 – l)Sili. Xt-i + ut, ist ein ADL(1, 0)-Modell mit korrelierten Störgrößen AR-Form des Modells der adaptiven Erwartung Yt = a(1 – l) + l. Yt-1 + b(1 – l)Xt + vt ist ein ADL(1, 0)-Modell mit korrelierten Störgrößen AR-Form des Modells der partiellen Anpassung Yt = ad + (1 – d)Yt-1 + bd. Xt + dut ist ein ADL(1, 0)-Modell mit unkorrelierten Störgrößen Das Modell Yt = Xtb + ut mit korrelierten Störgrößen ut = jut-1+ et kann geschrieben werden als Yt = j. Yt-1 + bj. Xt-1 + et; es ist ein ADL(1, 1)-Modell, wenn b 1 = b 0 j Hackl, Einführung in die Ökonometrie (17) 32

ADL(1, 0)-Modell: Stabilität Yt = a + j. Yt-1 + b. Xt + ut Effekt einer Änderung von X um DX = 1 Gleichgewichts-Zustand: n Voraussetzung für Summierbarkeit der Beiträge (die Erreichbarkeit des Gleichgewichts-Zustandes): |j| < 1; d. i. die Stationaritäts-Bedingung n Der Gleichgewichts-Zustand wird nur asymptotisch erreicht Periode DY t b t-1 jb t-2 j 2 b … … Summe b/(1 – j) Vergleiche das DL(s)-Modell: der Gleichgewichts-Zustand wird nach s Perioden erreicht Hackl, Einführung in die Ökonometrie (17) 33

Stabilität des ADL(1, 1)-Modells Welchen Wert Y* erreicht Y im Gleichgewichts-Zustand (X wird auf fixem Niveau X* gehalten)? Y* = a + j. Y* + b 0 X* + b 1 X* liefert Y* = a/(1 – j) + (b 0+ b 1)/(1 – j)X* Effekt einer Änderung von X um DX = 1: (b 0+ b 1)/(1 – j) Voraussetzung für die Erreichbarkeit des Gleichgewichts-Zustandes: |j| < 1 (Stationaritäts-Bedingung) d. h. , der dem Modell entsprechende AR(1)-Prozess Yt = a + j. Yt-1 + ut muss stationär sein Hackl, Einführung in die Ökonometrie (17) 34

Stabilität im ADL(p, s)-Modell F(L)Yt = a + b(L)Xt + ut mit F(L) = 1 – j 1 L – … – jp. Lp b(L) = 1 + b 1 L + … + bs. Ls Gleichgewichts-Effekt: (b 0+ … + bs)/(1 – j 1 – … – jp) Voraussetzung für die Erreichbarkeit des Gleichgewichts-Zustandes: n Siji < 1 (notwendig, aber nicht hinreichend) n Für Wurzeln aus F(z) = 1 – j 1 z – … – jpzp = (1 – l 1 z)… (1 – lpz) = 0, also l 1, …, lp, muss gelten: |zi| = | li-1 | > 1, i = 1, …, p Hackl, Einführung in die Ökonometrie (17) 35

Gleichgewicht und Fehlerkorrektur ADL(1, 1)-Modell für Gleichgewichts-Zustand: m 1: Gleichgewichts-Effekt (siehe oben) Fehlerkorrektur-Form: DYt = – (1 – j)(Yt-1 – m 0 – m 1 Xt-1) + b 0 DXt + ut mit DYt = Yt – Yt-1, analog DXt Interpretation: Änderungen DY sind 1. Effekt von Änderungen DX 2. Ausgleich der Abweichung vom Gleichgewichts-Zustand, d. i. der Gleichgewichts-Fehler Y – m 0 – m 1 X Hackl, Einführung in die Ökonometrie (17) 36