Wiskunde D Werkgroep Dynamische modellen Dynamische Modellen Verbinding

Wiskunde D Werkgroep Dynamische modellen Dynamische Modellen Verbinding tussen wiskunde, biologie, natuurkunde, scheikunde, …. . achtergrondinformatie voor docenten van experimenteerscholen wiskunde D

Wiskunde D Werkgroep Dynamische modellen Inhoudsopgave 1. Modelleren in het bètaonderwijs 2. Modelleren meer specifiek bij wiskunde 3. Van dynamisch model naar differentiaalvergelijking 4. Verantwoording en bronnen 2

Wiskunde D Werkgroep Dynamische modellen 1. Modelleren in het bètaonderwijs

Wiskunde D Werkgroep Dynamische modellen Computermodellen • Computermodellen worden gebouwd om greep te krijgen op complexe verschijnselen. – verschijnselen trekken zich weinig aan van disciplinegrenzen – 'de wetenschap' heeft vaak nog geen definitieve antwoorden, niet alles is voorspelbaar – doelen: • begrijpen, theorie ontwikkelen • optimaliseren • Voorspellen 4

Wiskunde D Werkgroep Dynamische modellen Wat zou een leerling moeten weten/kunnen? • Verband leggen tussen probleemsituatie, kwalitatief model en kwantitatief model • Samenhang zien tussen factoren in veranderingsproces • Zelf eenvoudige situaties kunnen modelleren • Modellen kritisch evalueren (betrouwbaarheid, grenzen, onzekerheden) 5

Wiskunde D Werkgroep Dynamische modellen Hoe kun je dat onderwijzen? • Computermodellen gebruiken en maken – voldoende complex: noodzaak tot vereenvoudiging – progressieve aanpak: model wordt steeds beter – uitkomst niet triviaal: noodzaak computergebruik • Vanuit het perspectief van de leerling – aanhaken bij bekende situatie/voorkennis – creëer een ‘need to know’ • Transfer naar nieuwe domeinen 6

Wiskunde D Werkgroep Dynamische modellen Wiskunde Dynamisch systeem: verandering in de tijd hangt af van huidige toestand • Computer nodig om uitkomsten te vinden • Reeksen, rijen, limieten • Tijdstappen • Integratiealgoritmen • Problemen in ‘context’ zonder veel aandacht voor de natuurwetenschappelijke uitwerking 7

Wiskunde D Werkgroep Dynamische modellen Natuurkunde • Beperkte set standaardproblemen (slinger, radioactief verval, afkoelende koffie) • Uitkomsten toetsen aan experiment • Veel grotere klasse van real world problemen, gedeeltelijk met dezelfde basiselementen (klimaat, raketvlucht) 8

Wiskunde D Werkgroep Dynamische modellen Biologie • Schoolvak in compex • Wiskunde lastig, ook voor docenten • Weinig toetsbaar, soms vooral een black box (animated conceptmap) • Veel variabelen, weerzin tegen vereenvoudiging • Vaak geen exacte waarden bekend • Chaos 9

Wiskunde D Werkgroep Dynamische modellen Scheikunde • In het schoolvak: beperkt aantal (industriële) evenwichtsreacties (ammoniaksynthese) • Niet-evenwichtssituaties komen nauwelijks aan de orde • Veel toepassingen in de randgebieden van de chemie: voedselhygiëne; farmacologie; atmosferische chemie 10

Wiskunde D Werkgroep Dynamische modellen Software voor grafisch modelleren • • Powersim/Stella/Coach 6/Dynasys/… Handig in de schetsfase Modellen beter uit te leggen/te presenteren Voordeel: samenhang tussen factoren in dynamisch proces eerst kwalitatief te modelleren, geleidelijke kwantificering in vergelijkingen • Nadeel: Moeilijk inzicht krijgen in rekenmechanisme 11

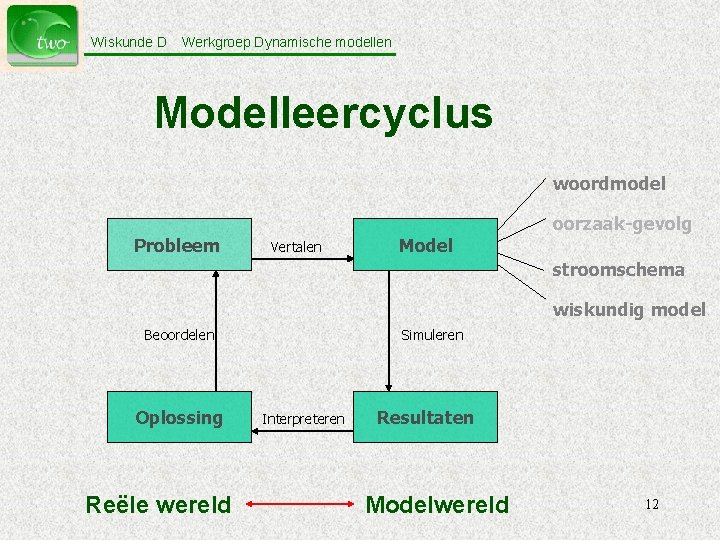
Wiskunde D Werkgroep Dynamische modellen Modelleercyclus woordmodel oorzaak-gevolg Probleem Vertalen Model stroomschema wiskundig model Beoordelen Oplossing Reële wereld Simuleren Interpreteren Resultaten Modelwereld 12

Wiskunde D Werkgroep Dynamische modellen 2. Modelleren meer specifiek bij wiskunde

Wiskunde D Werkgroep Dynamische modellen Modelleren • discrete modellen (vb. populatiedynamica) • continue modellen (vb. afkoelingsproces) • verandering centraal • in nieuwe plannen aandachtspunt van meerdere disciplines (NLT-module) • geschikt voor vakoverstijgend en thematisch onderwijs 14

Wiskunde D Werkgroep Dynamische modellen Dynamisch model • Beschrijving van een dynamisch systeem • Samenhang tussen variabelen, die elkaar beïnvloeden (feedback) • Vraag naar ontwikkeling in de loop van de tijd 15

Wiskunde D Werkgroep Dynamische modellen Grafische modelleeromgeving • kwalitatief ontwikkelen van een model in de vorm van een stroomschema • uitvoer als grafiek en als tabel • eenvoudige aanpassing van model en variatie van parameters voor simulatie • onderzoek naar evenwicht • invloed parameters en beginwaarden 16

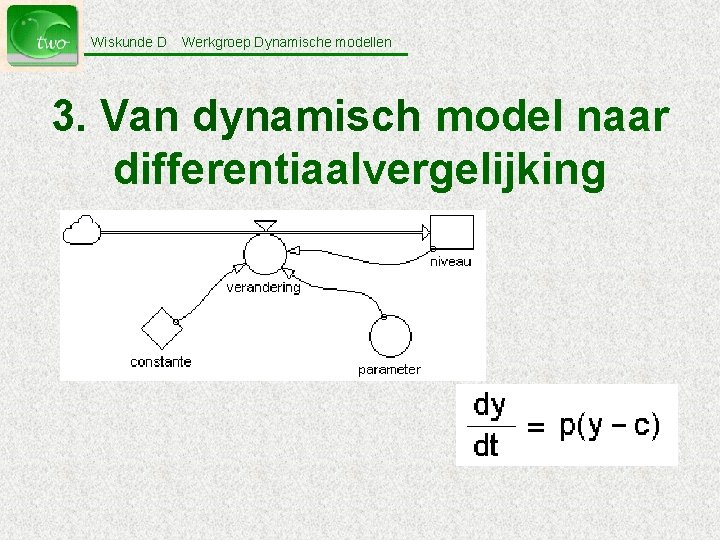
Wiskunde D Werkgroep Dynamische modellen 3. Van dynamisch model naar differentiaalvergelijking

Wiskunde D Werkgroep Dynamische modellen Hoe zit het in elkaar ? • van kwalitatief ontwerp naar kwantitatief resultaat door opstellen van formules voor samenhang • stelsel van modelvergelijkingen • numerieke integratie (Euler-Cauchy of Runge-Kutta methode • differentiaalvergelijkingen 18

Wiskunde D Werkgroep Dynamische modellen Voorbeeld 1 Modellering van het afkoelingsproces van een hete drank

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (1) • hete koffie van 80°C afkoelen, zo dat elke tijdseenheid de temperatuur 2 graden daalt. 20

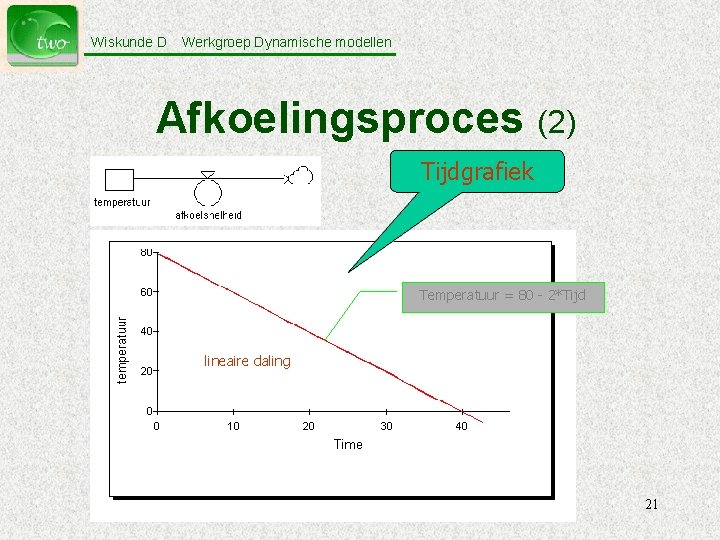
Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (2) Tijdgrafiek Temperatuur = 80 - 2*Tijd lineaire daling 21

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (3) • Kritiek op model n de temperatuur van de drank blijft niet eeuwig dalen n de temperatuur van de drank wordt begrensd door de omgevingstemperatuur n de snelheid waarmee de temperatuur daalt is niet constant n een lineaire afname is daarom niet realistisch 22

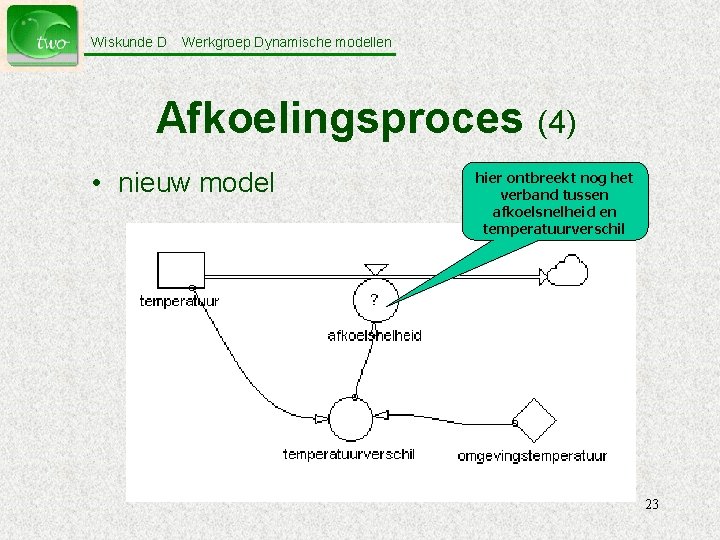
Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (4) • nieuw model hier ontbreekt nog het verband tussen afkoelsnelheid en temperatuurverschil 23

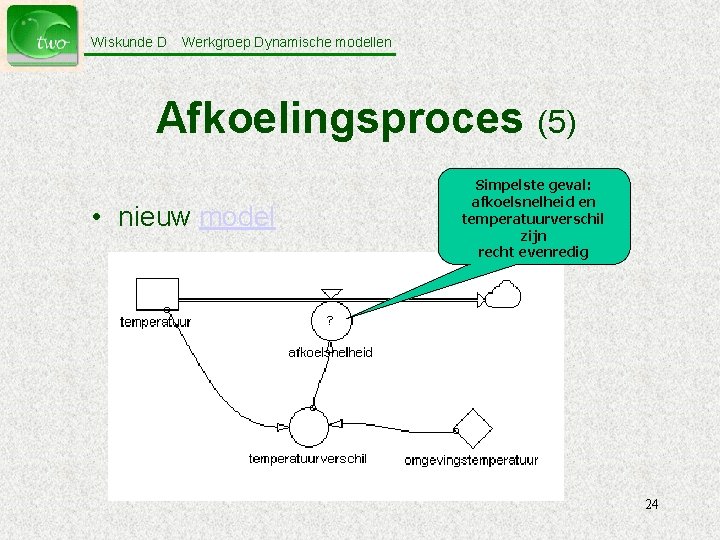
Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (5) • nieuw model Simpelste geval: afkoelsnelheid en temperatuurverschil zijn recht evenredig 24

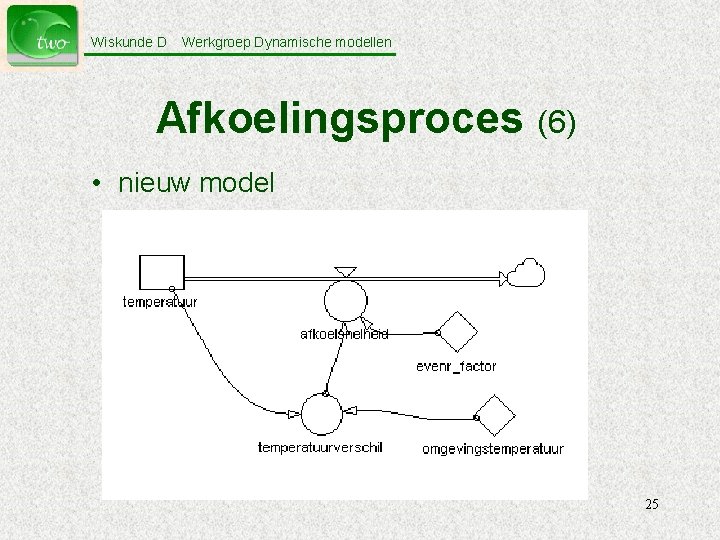
Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (6) • nieuw model 25

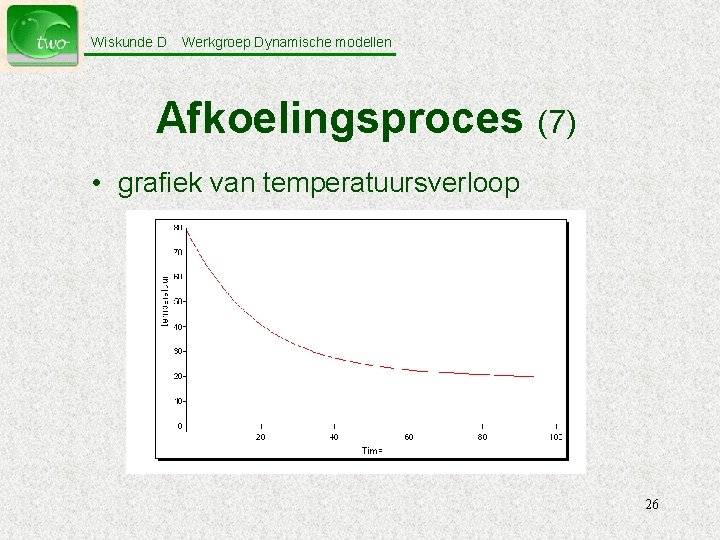
Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (7) • grafiek van temperatuursverloop 26

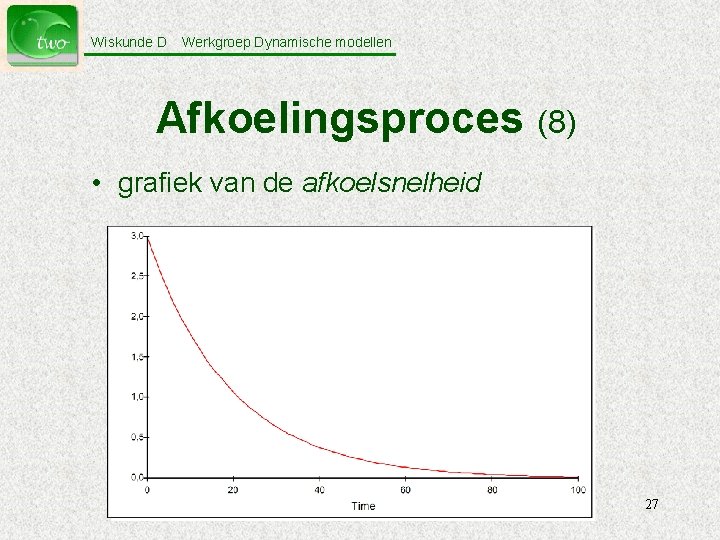
Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (8) • grafiek van de afkoelsnelheid 27

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (9) • Modelvergelijkingen 28

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (10) • Van modelvergelijking naar differentiaalvergelijking niveauvergelijking temperatuur. nieuw = temperatuur. oud - deltat*(afkoelsnelheid) beginwaarde temperatuur = 80 met als limiet 29

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (11) • differentiaalvergelijking verandering afkoelsnelheid = evenr_factor*temperatuurverschil constante omgevingstemperatuur = 20 evenr_factor = - 0. 05 hulpvariabele temperatuurverschil = temperatuur -omgevingstemperatuur 30

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (12) • VU-Grafiek geeft het richtingsveld van de differentiaalvergelijking : 31

Wiskunde D Werkgroep Dynamische modellen Afkoelingsproces (13) • na het kiezen van een beginwaarde krijg je de specifieke oplossingskromme 32

Wiskunde D Werkgroep Dynamische modellen Voorbeeld 2 Modellering van een kweekvijver

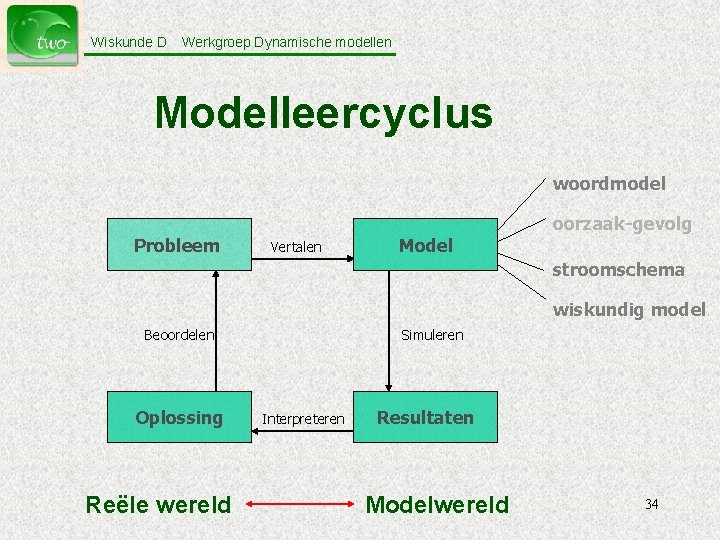
Wiskunde D Werkgroep Dynamische modellen Modelleercyclus woordmodel oorzaak-gevolg Probleem Vertalen Model stroomschema wiskundig model Beoordelen Oplossing Reële wereld Simuleren Interpreteren Resultaten Modelwereld 34

Wiskunde D Werkgroep Dynamische modellen De forellenvijver • In een vijver met 180 hl water zwemmen 150 forellen. Per minuut stroomt er 20 liter water de vijver in. Hierdoor komen er per 750 liter ook gemiddeld 3 forellen bij. • Het waterniveau wordt op peil gehouden door een afvoer van 18 liter water per minuut. Hierdoor verdwijnen er ook forellen. Het aantal is evenredig met het aantal forellen in de vijver en de hoeveelheid wegstromend water. • Hoe ontwikkelt de forellenpopulatie zich onder deze omstandigheden? 35

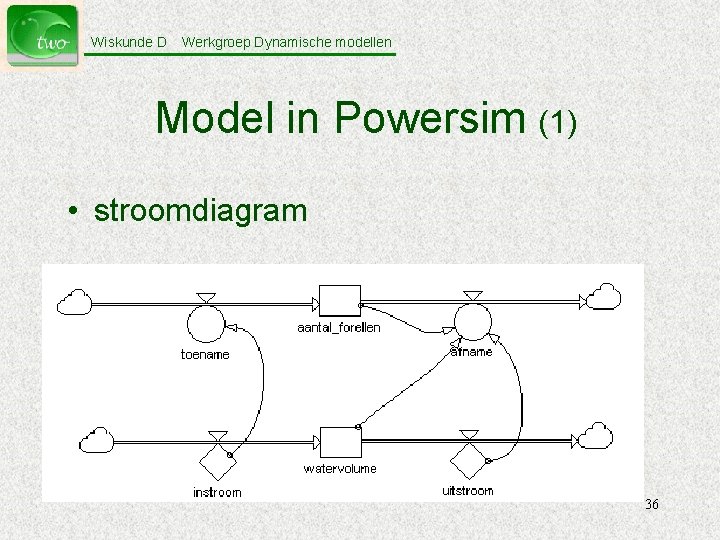
Wiskunde D Werkgroep Dynamische modellen Model in Powersim (1) • stroomdiagram 36

Wiskunde D Werkgroep Dynamische modellen Model in Powersim (2) • modelvergelijkingen 37

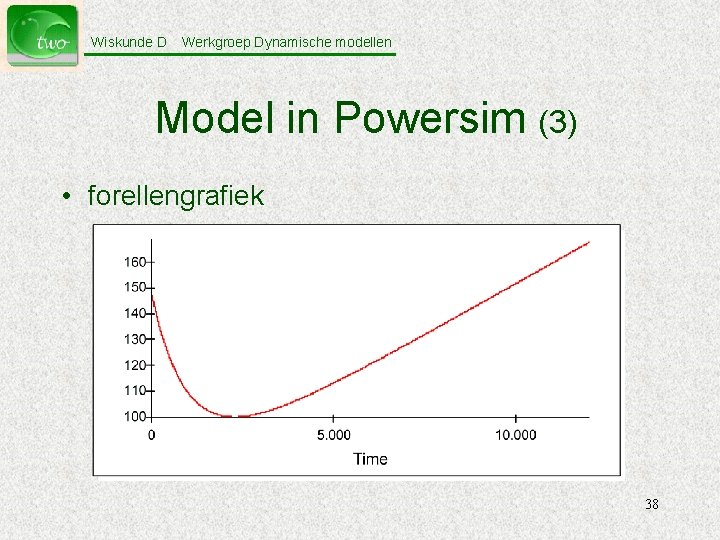
Wiskunde D Werkgroep Dynamische modellen Model in Powersim (3) • forellengrafiek 38

Wiskunde D Werkgroep Dynamische modellen Differentiaalvergelijking opstellen (1) forellen. nieuw = forellen. oud + dt*(toename - afname ) instroom = 20 toename = instroom*3/750 = 0, 08 39

Wiskunde D Werkgroep Dynamische modellen Differentiaalvergelijking opstellen (2) • forellen. nieuw = forellen. oud + dt*(toename - afname ) afname = forellen/water*uitstroom = 18 afname = y(t)*18/water 40

Wiskunde D Werkgroep Dynamische modellen Differentiaalvergelijking opstellen (3) • forellen. nieuw = forellen. oud + dt*(toename - afname ) beginwaarde water = 18000 water. nieuw = water. oud + dt*(instroom - uitstroom) lineair verband ! water(t) = beginwater + t(20 -18) water(t) = 18000 + 2 t 41

Wiskunde D Werkgroep Dynamische modellen Differentiaalvergelijking opstellen (4) • forellen. nieuw = forellen. oud + dt*(toename - afname ) 42

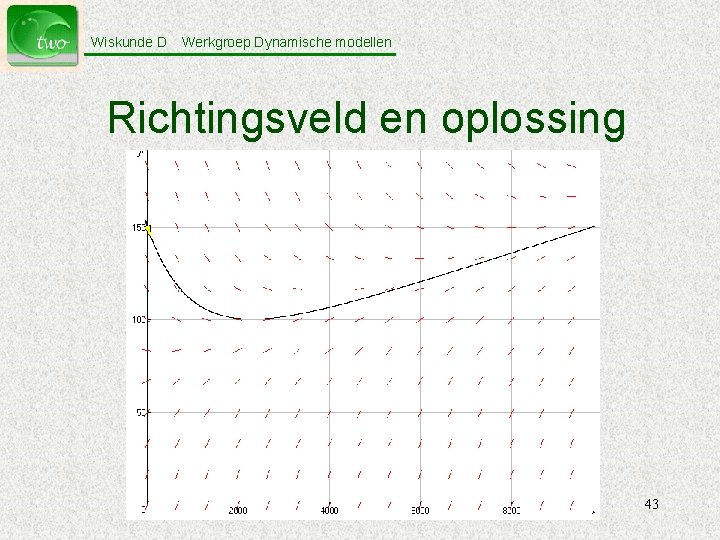
Wiskunde D Werkgroep Dynamische modellen Richtingsveld en oplossing 43

Wiskunde D Werkgroep Dynamische modellen Beperkingen van het model • Constante toename van aantal forellen realistisch? • Vijver heeft een maximale capaciteit • Biologische populatiegroei niet meegenomen • . . . 44

Wiskunde D Werkgroep Dynamische modellen 4. Verantwoording en bronnen Voor deze presentatie is onder meer gebruik gemaakt van materiaal ontwikkeld door: Nol Gregor, Elwin Savelsbergh en Carel van de Giessen

Wiskunde D Werkgroep Dynamische modellen Bronnen • Literatuur • Websites – – www. ctwo. nl www. wisweb. nl www. cdbeta. uu. nl/model www. cdbeta. uu. nl/vo/salvo 46

Wiskunde D Werkgroep Dynamische modellen Literatuur • Hannon, Bruce Ruth, Matthias Dynamic Modeling Springer Verlag, 1994 • Heesterbeek, Hans e. a. De wiskundige kat, de biologische muis en de jacht op inzicht Epsilon Uitgaven, 2004 • Bossel, Hartmut Modellbildung und Simulation Braunschweig, 1994 47

Wiskunde D Werkgroep Dynamische modellen Einde van deze presentatie ! 48