Kapitel 22 VARProzesse und VECModelle Hackl Einfhrung in

Kapitel 22 VAR-Prozesse und VEC-Modelle Hackl, Einführung in die Ökonometrie (22)

VAR-Modell Multivariates autoregressives oder VAR-Modell: Verallgemeinerung des autoregressiven Modells Yt = j. Yt-1 + ut: A yt = m + P yt-1 + ui mit m-Vektoren yt = (Yt 1, …, Ytm)‘, m und ut und (mxm)-Matrix P VAR(1)-Modell: die Ordnung des Modell beträgt 1 Bei geeigneter Wahl von y: dynamische Version eines simultanen Mehrgleichungs-Modells (siehe unten) Hackl, Einführung in die Ökonometrie (22) 2

Beispiel: Einkommen und Konsum seien durch folgendes Modell beschrieben: Yt = m 1 + p 11 Yt-1 + p 12 Ct-1 + u 1 t Ct = m 2 + p 21 Ct-1 + p 22 Yt-1 + u 2 t Mit y = (Y, C)‘ und analogen Größen m, u und (2 x 2)-Matrix P können die beiden Gleichungen geschrieben werden als yt = m + P yt-1 + ut Die Koeffizienten-Matrix P und der Vektor m der Interzepte enthält die entsprechenden Parameter aus den beiden Gleichungen Gleiches wäre möglich, wenn das Modell eine weitere (exogene) Variable enthält Hackl, Einführung in die Ökonometrie (22) 3

Simultanes Mehrgleichungs. Modell als VAR-Modell Simultanes Mehrgleichungs-Modell mit vorherbestimmten Regressoren A yt = G zt + ut = G 1 yt-1 + G 2 xt + ut zt enthält um eine Periode verzögerte endogene Variable yt-1 und exogene Variable xt Durch Umformen ergibt sich yt = P yt-1 + mt + vt mit P = A-1 G 1, mt = A-1 G 2 xt und vt = A-1 ut Achtung! Erweitern des Vektors y um in mt enthaltene Regressoren erlaubt es, das Modell mit von t unabhängigem m zu schreiben Hackl, Einführung in die Ökonometrie (22) 4

VAR-Modell: OLS-Schätzer Das VAR(1)-Modell yt = m + P yt-1 + ut stellt jede Komponente von y als Linearkombination verzögerten Variablen dar Annahmen: n Die Störgrößen sind möglicherweise kontemporär, aber nicht intertemporär korreliert n Die Komponenten von y sind stationäre Zeitreihen Die Voraussetzungen der OLS-Schätzung sind erfüllt, die OLS-Schätzer der Koeffizienten jeder Gleichung sind BLU-Schätzer Hackl, Einführung in die Ökonometrie (22) 5

Einkommen und Konsum, Forts. AWM-Datenbasis: PCR (realer Privater Konsums), PYR (reales Verfügbares Einkommen der Haushalte); C, Y: jährliche Zuwachsraten Anpassen von yt = m + P yt-1 + ut mit y = (Y, C)‘ gibt Y C m Y-1 C-1 adj. R 2 AIC pij 0. 001 0. 825 0. 082 0. 80 -6. 94 t(pij) 0. 91 12. 09 1. 07 pij 0. 003 0. 061 0. 826 0. 79 -7. 16 t(pij) 2. 36 0. 97 11. 69 mit AIC = -14. 41 Zum Vergleich: Ĉ = 0. 011 + 0. 718 Y mit t(Y) = 15. 55, adj. R 2 = 0. 65 und AIC = -6. 61 Hackl, Einführung in die Ökonometrie (22) 6

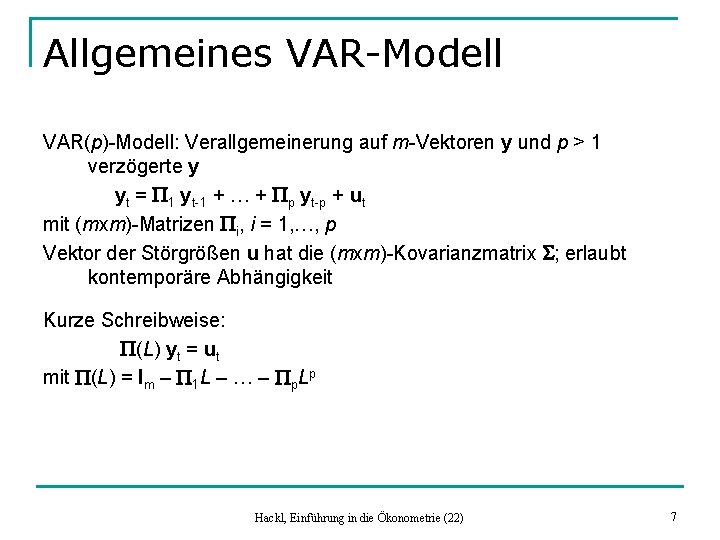
Allgemeines VAR-Modell VAR(p)-Modell: Verallgemeinerung auf m-Vektoren y und p > 1 verzögerte y yt = P 1 yt-1 + … + Pp yt-p + ut mit (mxm)-Matrizen Pi, i = 1, …, p Vektor der Störgrößen u hat die (mxm)-Kovarianzmatrix S; erlaubt kontemporäre Abhängigkeit Kurze Schreibweise: P(L) yt = ut mit P(L) = Im – P 1 L – … – Pp. Lp Hackl, Einführung in die Ökonometrie (22) 7

VAR-Modell: Vorteile Neben der großen Allgemeinheit: n Erfüllt Annahmen, die der OLS-Schätzung zugrunde liegen n Erfordert keine Unterscheidung von endogen und exogenen Variablen (Abgrenzung ist stets willkürlich) n Erlaubt das Berücksichtigen von Nicht-Stationarität und Kointegration; siehe unten zum Fehlerkorrektur-Modell Achtung! Die Anzahl der zu schätzenden Parameter wächst rasch mit m und p Zahl der Elemente von P für Werte von m und p p 1 2 3 m=2 4 8 12 m=4 16 32 56 Hackl, Einführung in die Ökonometrie (22) 8

Kointegration Stationärer AR(1)-Prozess Yt = j. Yt-1 + ut: für die Wurzel des charakteristischen Polynoms 1 – jz = 0 gilt |z| > 1; daraus folgt |j| < 1 Gilt j = 1, so liegt Nicht-Stationarität vor: Y ist integriert; stochastischer Trend Zwischen mehreren, nicht-stationären Variablen mit gleicher Ordnung der Integration kann eine kointegrierende Beziehung bestehen Hackl, Einführung in die Ökonometrie (22) 9

Kointegration beim VAR(p)Prozess VAR(p)-Prozess ist stationär, wenn für alle Wurzeln zj des charakteristischen Polynoms det P(z) = 0 gilt: |zj| > 1; det P: Determinante von P Sind die Pi (mxm)-Matrizen, so gibt es mp Wurzeln Ist z = 1 eine (mehrfache) Wurzel: nicht-stationärer VAR-Prozess Hackl, Einführung in die Ökonometrie (22) 10

VAR(1)-Prozess mit m=2 VAR(1)-Modell für 2 -komponentigen Vektor y: charakteristisches Polynom zur Matrix P(z) = I – P z hat 2 Wurzeln: a) Haben beide Wurzeln von P(z) = 0 den Wert Eins, so sind beide Variablen in y integriert; es gibt zwischen ihnen keine kointegrierende Beziehung b) Hat genau eine der beiden Wurzeln den Wert Eins, so sind die Variablen kointegriert c) Hat keine der Wurzeln den Wert Eins, so sind beide Variablen stationär; es gibt natürlich keine kointegrierende Beziehung Das illustriert das folgende Beispiel Hackl, Einführung in die Ökonometrie (22) 11

Beispiel X und Y seien beschrieben durch Xt + a. Yt = u 1 t, u 1 t = r 1 u 1, t-1 + e 1 t (A) Xt + b. Yt = u 2 t, u 2 t = r 2 u 2, t-1 + e 2 t (B) mit a ≠ b und unabhängigen IID(0, si 2)-Prozessen ei, i = 1, 2 Reduzierte Form: X und Y sind Linearkombinationen von u 1 und u 2 Das VAR(1)-Modell ergibt sich zu Xt = (r 1 – ad)Xt-1 – abd. Yt-1 + v 1 t Yt = d. Xt-1 + (r 1 + bd)Yt-1 + v 2 t mit d = (r 1 – r 2)/(a – b) und Linearkombinationen vi der ei Das charakteristisches Polynom det P(z) = 1 – z(r 1 – r 2) + z 2 r 1 r 2 = 0 hat die Wurzeln z 1 = 1/r 1 und z 2 = 1/r 2 Hackl, Einführung in die Ökonometrie (22) 12

Beispiel, 1. 2. 3. Forts. Seien r 1 = 1, |r 2 | < 1; d. h. , u 1 ~ I(1), u 2 ~ I(0); dann gilt z 1 = 1, z 2 > 1; aus der reduzierten Form folgt, dass X ~ I(1) und Y ~ I(1), also beide nicht-stationär sind; Gleichung (B) zeigt, dass X und Y kointegriert sind; siehe Fall b) |r 1| < 1, |r 2 | < 1; d. h. , u 1 ~ I(0), u 2 ~ I(0); also sind u 1, u 2 und auch X und Y stationäre Prozesse; siehe Fall c) Seien r 1 = r 2 = 1; beide Wurzeln z 1 und z 2 haben den Wert 1; u 1 und u 2 sind nicht-stationäre Prozesse, ebenfalls X und Y; es gibt zwischen ihnen keine kointegrierende Beziehung; siehe Fall a) Hackl, Einführung in die Ökonometrie (22) 13

Kointegration beim VAR(p)Prozess, Forts. VAR(1)-Modell für m-komponentigen Vektor y: Existieren m – r Wurzeln des charakteristisches Polynoms det P(z) = 0, die den Wert Eins haben, so bestehen r kointegrierende Beziehungen Hackl, Einführung in die Ökonometrie (22) 14

Beispiel, Forts. Darstellung in Differenzen im Fall r 1 = 1: es ergeben sich DXt = – ad Xt-1 – abd Yt-1 + v 1 t DYt = d Xt-1 + bd Yt-1 + v 2 t In Matrix-Schreibweise wird aus dem Modell yt = P yt-1 + m + ut das Modell Dyt = – (I – P) yt-1 + m + ut = – P(1) yt-1 + m + ut mit der Matrix Hackl, Einführung in die Ökonometrie (22) 15

Granger's Repräsentations. Theorem Darstellung des VAR(1)-Modells yt = P yt-1 + m + ut als Dyt = – P(1) yt-1 + m + ut r (P(1)): Rang von P(1) 1. 2. 3. Bei r (P(1)) = 0 ergibt sich Dyt = + m + ut; d. h. , y ist ein mdimensionaler random walk; jede Komponente ist I(1)-integriert; es gibt keine kointegrierende Beziehung Bei r (P(1)) = r < m existiert eine (m – r)-fache Wurzel Eins; es können (mxr)-Matrizen H und J vom Rang r gefunden werden mit P(1) = HJ‘ es gibt r kointegrierende Beziehungen; die Spalten von J sind die kointegrierenden Vektoren (bei standardisierter Form von J, d. h. , die Hauptdiagonal-Elemente von J sind Einsen) Bei r (P(1)) = m ist der VAR(1)-Prozess stationär, y ist I(0)-integriert Hackl, Einführung in die Ökonometrie (22) 16

Granger's Repräsentations. Theorem, Forts. Der VAR(1)-Prozess, dargestellt als Dyt = – P(1) yt-1 + m + ut, erfülle P(1) = HJ‘ mit r (P(1)) = r < m; dann gilt 1. Dyt ist stationär 2. J‘ yt ist stationär; jede der r Spalten von J definiert eine kointegrierende Beziehung yt besteht aus m-r linear unabhängigen deterministischen und r unabhängigen stochastischen Trends Vektor-Fehlerkorrektur- oder VEC-Modell: Dyt = – HJ‘ yt-1 + m + ut Kointegrations-Rang: r Adaptionsparameter: Elemente von H Hackl, Einführung in die Ökonometrie (22) 17

Beispiel, Forts. Im Fall r 1 = 1 ergibt sich Die standardisierte Form von J ist J = (1 b)‘ Die kointegrierende Beziehung ergibt sich zu J‘yt-1 = Xt-1 + b. Yt-1 Hackl, Einführung in die Ökonometrie (22) 18

Das VEC(1)-Modell Die Darstellung des VAR(1)-Modells als Vektor-Fehlerkorrektur- oder VEC-Modell Dyt = – HJ‘ yt-1 + m + ut beschreibt Änderungen Dy als Funktion n des Interzept-Vektors n der r Gleichgewichts-Beziehungen Abweichungen vom Gleichgewicht in der Periode t -1 werden in der Periode t teilweise korrigiert; vergleiche das negative Vorzeichen von HJ‘ yt-1 Adaptionsparameter (Elemente von H): geben den Anteil der Korrektur an und sind ein Maß für die Geschwindigkeit, mit der die Korrektur vorgenommen wird Hackl, Einführung in die Ökonometrie (22) 19

Das VEC(p)-Modell Das Representations-Theorem von Granger und die Darstellung als VEC-Modell gelten auch für den VAR(p)-Prozess P(L) yt = m + ut wegen P(L) = – P(1) L + (1 – L) Y(L) und P(1) = HJ‘ kann das VAR(1)-Modell als VEC(p)-Modell Dyt = – Y 1 Dyt-1 – … – Yp. Dyt-p – HJ‘ yt-1 + m + ut geschrieben werden, wenn r (P(1)) = r < m die Spalten von J sind die kointegrierenden Vektoren, welche die r kointegrierenden Beziehungen von y definieren Hackl, Einführung in die Ökonometrie (22) 20

Schätzen des VEC-Modells Voraussetzung: y ~ I(1) Schätzen der Parameter: 1. Spezifikation von Interzepten und deterministischen Trends q in den Komponenten von yt und q in den kointegrierenden Beziehungen 2. Wahl des Kointegrations-Ranges r, etwa mittels R 3 -Methode von Johansen (siehe unten) 3. Schätzen der kointegrierenden Beziehungen, Standardisieren 4. Schätzen des VEC-Modells Hackl, Einführung in die Ökonometrie (22) 21

Johansen‘s R 3 -Methode Reduced rank regression oder R 3 -Methode, auch Johansen's Test genannt: iteratives Verfahren zum Festlegen des Kointegrations. Ranges r Idee der R 3 -Methode: n Schätzen von P(1) n Test, ob Restriktionen zutreffen, die den Rang reduzieren Testverfahren von H 0: li = 0, i = r+1, …, m (d. h. : Kointegrations-Rang beträgt r) die li sind Eigenwerte von Y 1‘Y 1 – Y 1 DY(DY‘DY)-1 DY‘Y 1 mit DY: Matrix der Differenzen Dy, Y 1: (nxm)-Matrix der yt-1 n Spur-Test (trace-Test) n Max-Test Hackl, Einführung in die Ökonometrie (22) 22

Tests zum Kointegrations-Rang Likelihood-Quotienten Tests unter Annahme normalverteilter Störgrößen 1. Spur-Test (trace-Test): testet für j = 0, 1, … Hj: r (P(1)) = j gegen Hm: r (P(1)) = m solange, bis zum ersten Mal die Nullhypothese verworfen wird; dieses j ist der Kointegrations-Rang LR-Teststatistik Tjs = – 2[log Lj – log Lm] = – n Smi=j+1 log(1 – Îi) s in Tjs steht für „Spur“; die Teststatistik wird auch Trace-Statistik genannt Îi: Schätzer von li Kritische Schranken aus Simulationen Hackl, Einführung in die Ökonometrie (22) 23

Tests, Forts. Likelihood-Quotienten Tests unter Annahme normalverteilter Störgrößen 2. Max-Test: testet für j = 0, 1, … Hj: r (P(1)) = j gegen Hj+1: r (P(1)) = j+1 solange, bis zum ersten Mal die Nullhypothese verworfen wird; dieses j ist der Kointegrations-Rang LR-Teststatistik Tjm = – 2[log Lj – log Lj+1] = – n log(1 – Îj+1) m in Tjm steht für „Maximum“; die Teststatistik wird auch Max. Statistik genannt Îi: Schätzer von li Kritische Schranken aus Simulationen Hackl, Einführung in die Ökonometrie (22) 24

Einkommen und Konsum, Forts. AWM-Datenbasis: PCR (realer Privater Konsums), PYR (reales Verfügbares Einkommen der Haushalte); C, Y: logarithmierte Werte von PCR, PYR 1. Prüfen der Voraussetzung, dass C und Y nicht-stationär sind: C ~ I(1), Y ~ I(1) 2. Johansen-Test auf Kointegration: Für den Fall, dass C und Y keine Trends und die kointegrierende Beziehung ein Interzept haben, ergeben sich r = 1 (p < 0. 05) und die kointegrierende Beziehung C = 8. 55 – 1. 61 Y mit t(Y) = 18. 2 Hackl, Einführung in die Ökonometrie (22) 25

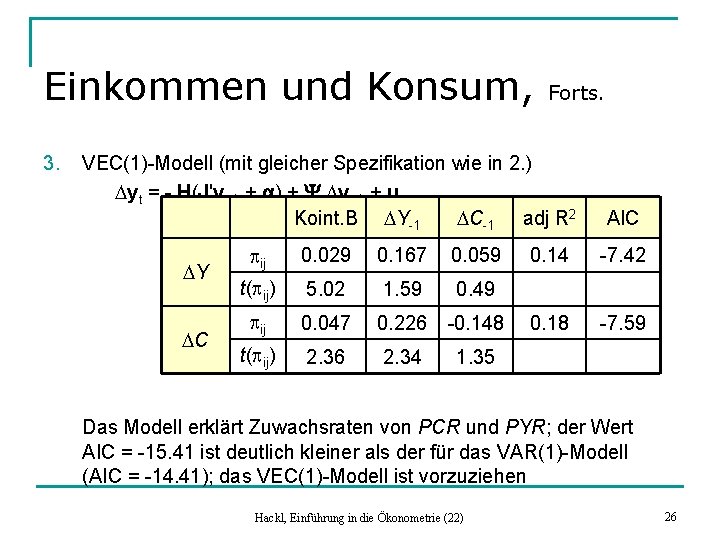
Einkommen und Konsum, 3. Forts. VEC(1)-Modell (mit gleicher Spezifikation wie in 2. ) Dyt = - H(J'yt-1 + a) + Y Dyt-1 + ut Koint. B DY-1 DC-1 adj R 2 DY DC pij 0. 029 0. 167 0. 059 t(pij) 5. 02 1. 59 0. 49 pij 0. 047 0. 226 -0. 148 t(pij) 2. 36 2. 34 1. 35 AIC 0. 14 -7. 42 0. 18 -7. 59 Das Modell erklärt Zuwachsraten von PCR und PYR; der Wert AIC = -15. 41 ist deutlich kleiner als der für das VAR(1)-Modell (AIC = -14. 41); das VEC(1)-Modell ist vorzuziehen Hackl, Einführung in die Ökonometrie (22) 26