IV Projection A projection transformation moves from three













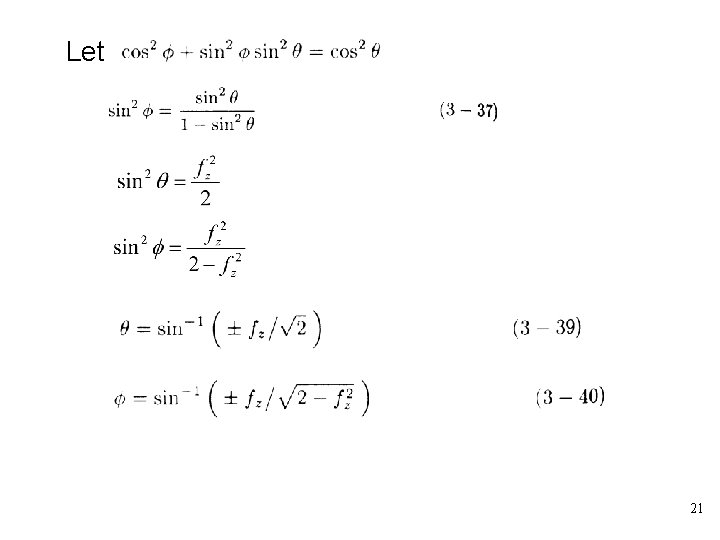































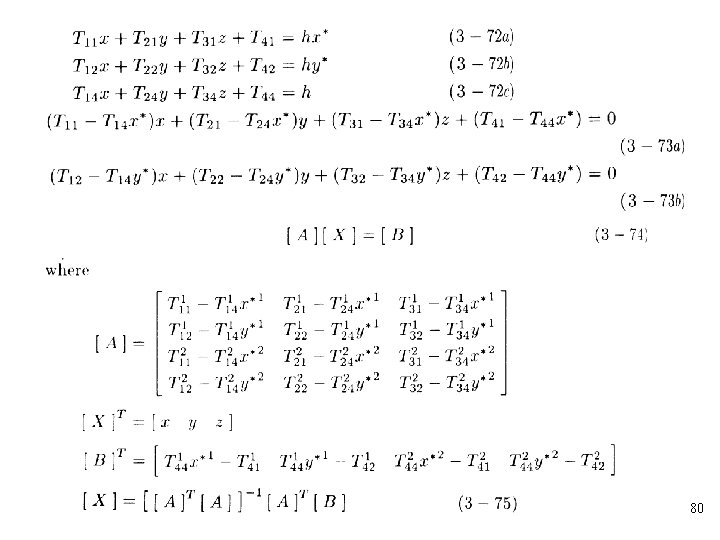




- Slides: 86

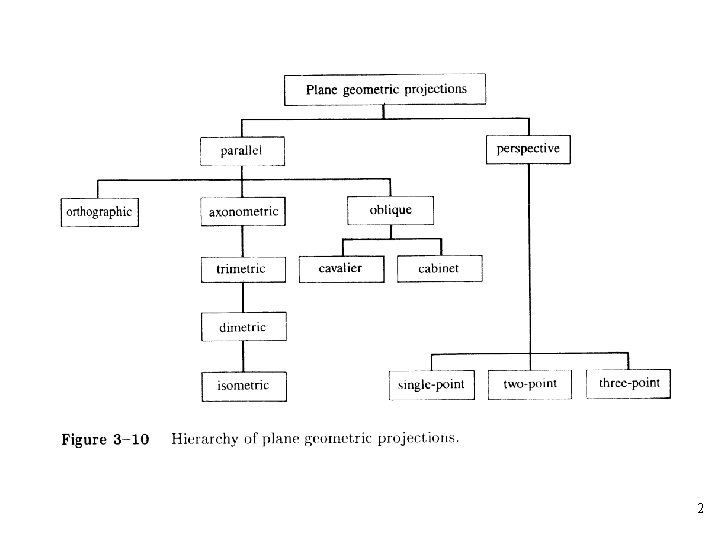
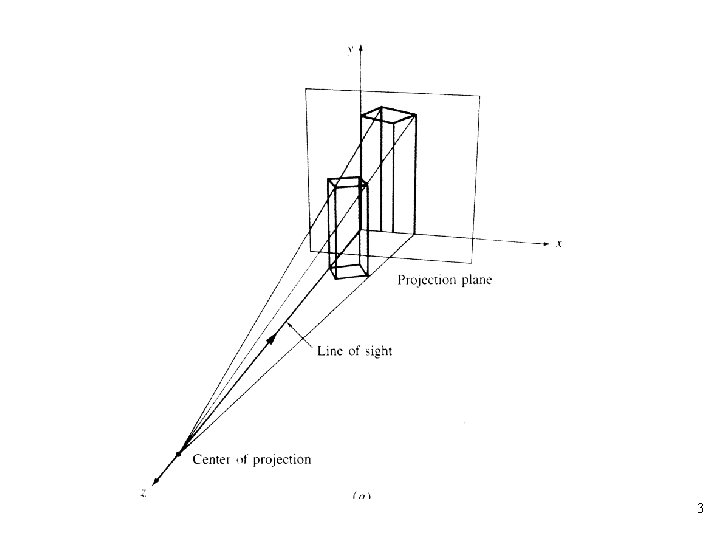
IV Projection • A projection transformation moves from three dimensions to two dimensions • Projections occur based on the viewpoint and the viewing direction • Projections move objects onto a projection plane • Projections are classified based on the direction of projection, the projection plane normal, the view direction, and the viewpoint • Two primary classifications are parallel and perspective 1

2

3

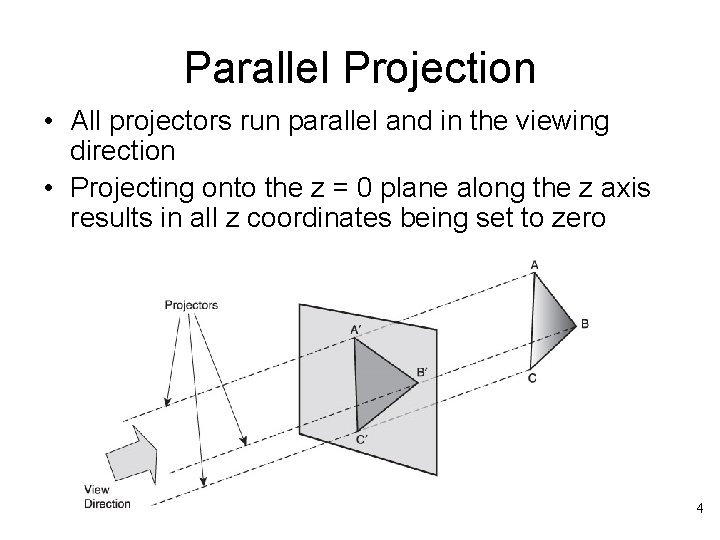
Parallel Projection • All projectors run parallel and in the viewing direction • Projecting onto the z = 0 plane along the z axis results in all z coordinates being set to zero 4

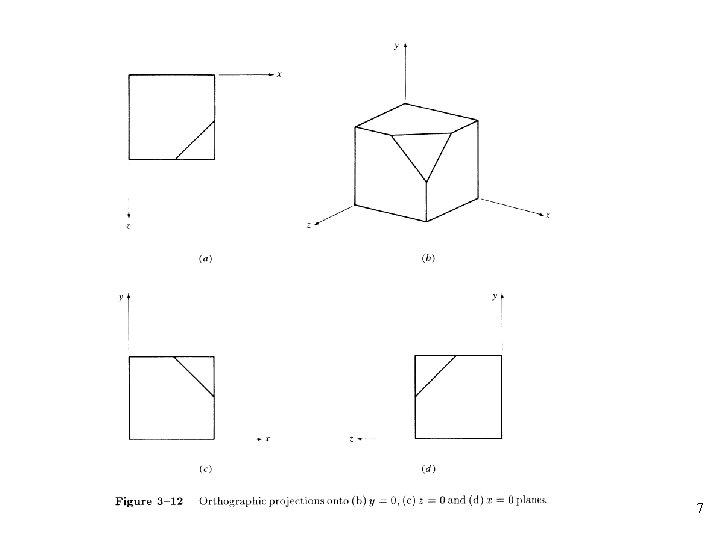
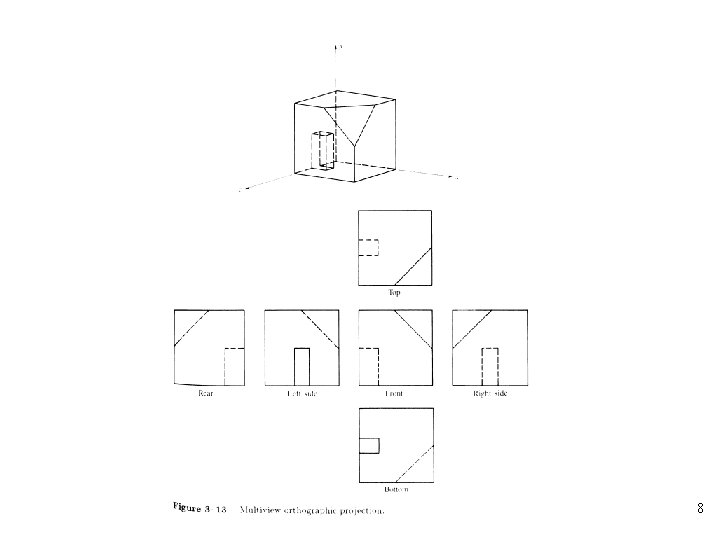
Orthographic Projection • The simplest of the parallel projections, which is commonly used for engineering drawings • They accurately show the correct or true size and shape of a single plane face of an object • The matrix for projection onto the x=0 plane • The matrix for projection onto the y=0 plane 5

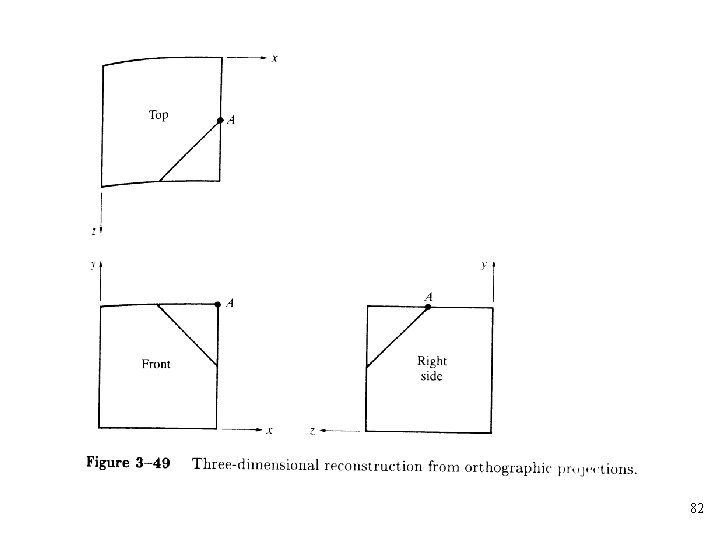
• The matrix for projection onto the z=0 plane • The centers of projection are at infinity • A single orthographic projection does not provide sufficient information to visually and practically reconstruct the shape of an object 6

7

8

9

10

11

12

13

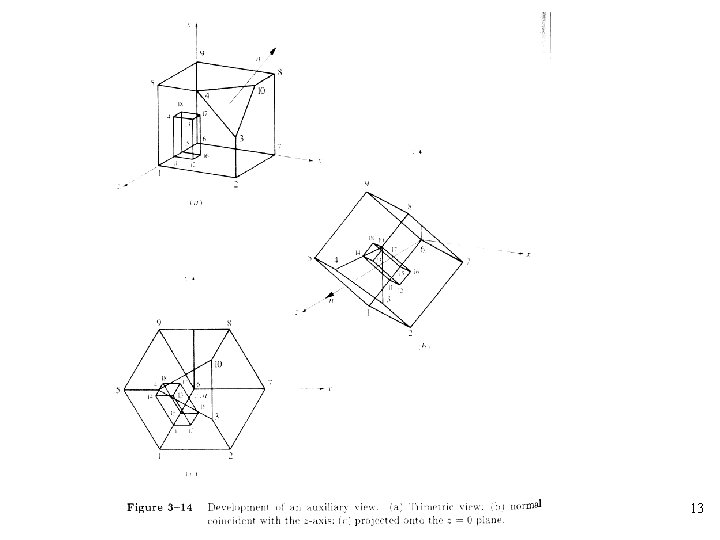
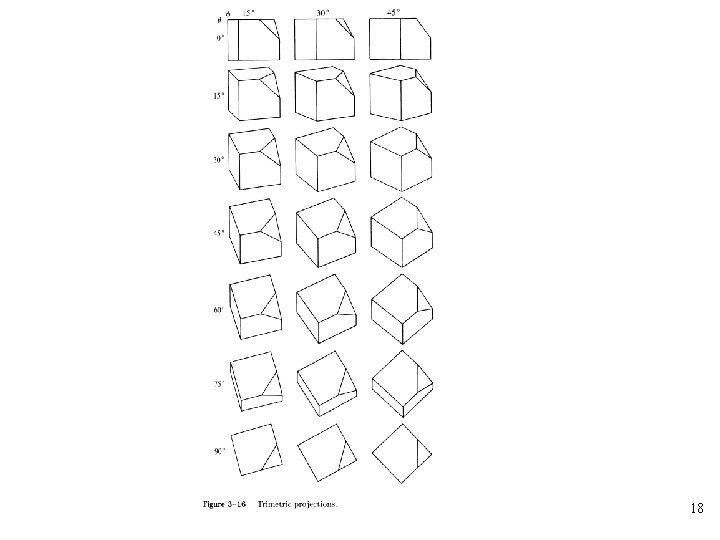
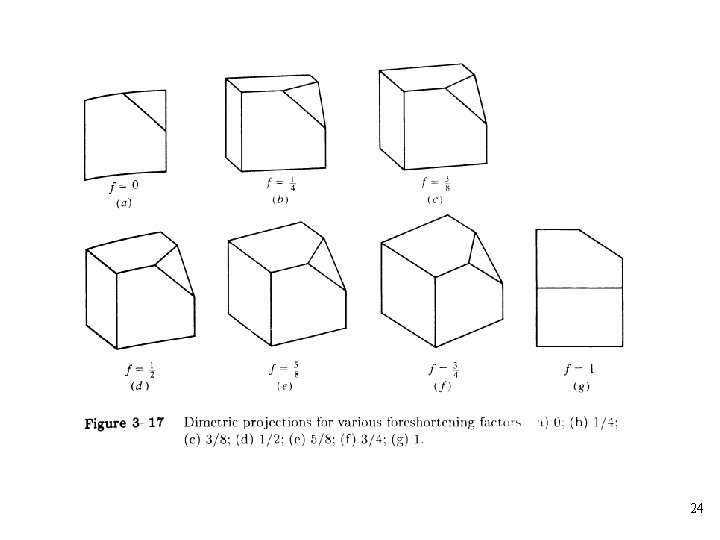
Axonometric Projection • An axonometric projection is constructed by manipulating the object, using rotations and translations, such that at least three adjacent faces are shown • The center of projection is at infinity • Unless a face is parallel to the plane of projection, an axonometric projection does not show its true shape • The foreshortening factor is the ratio of the projected length of a line to its true length • There are three axonometric projections of interest: trimetric, diametric, and isometric 14

• An isometric projection is a special case of a diametric projection, and a diametric projection is a special case of a trimetric projection • Foreshortening factors along the projected principal axes are: • A trimetric projection is formed by arbitrary rotations, in arbitrary order, about any or all of the coordinate axes, followed by parallel projection onto the z=0 plane 15

16

17

18

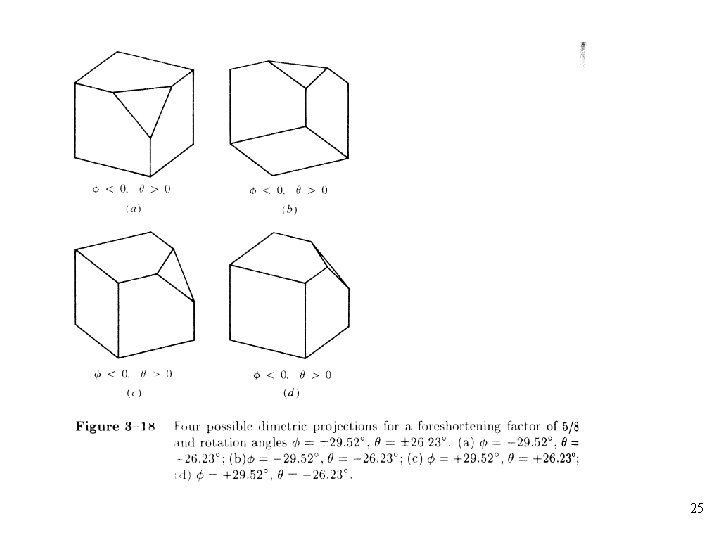
• A dimetric projection is a trimetric projection with two of the three foreshortening factors equal; the third is arbitrary • For example, a dimetric projection is constructed by a rotation about the y-axis through an angle followed by rotation about the x-axis through an angle and projection from a center of projection at infinity onto the z=0 plane: 19

20
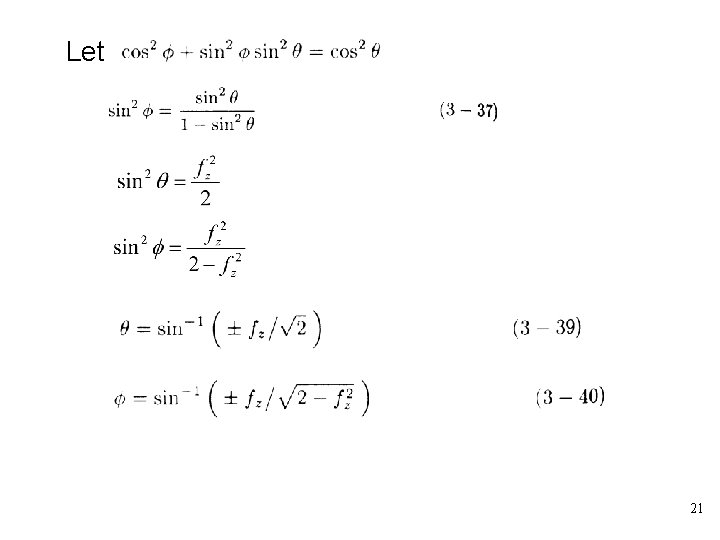
Let 21

22

23

24

25

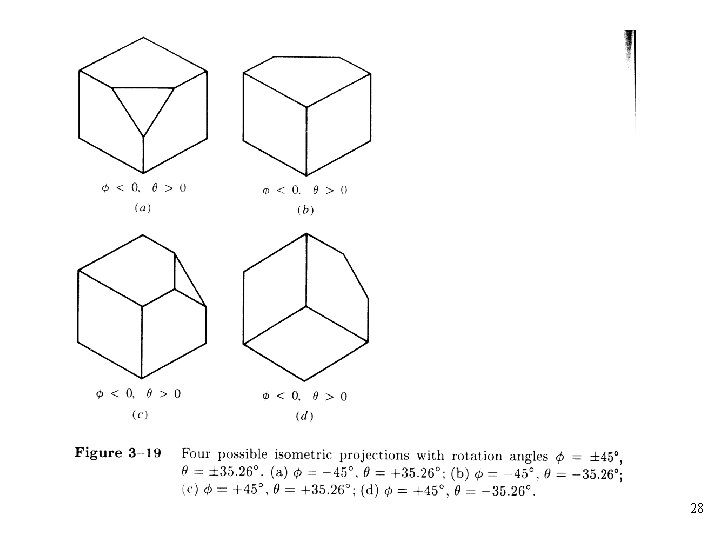
• Isometric projection: All three foreshortening factors are equal • The foreshortening factor: • The angle that the projected x-axis makes with the horizontal is 26

27

28

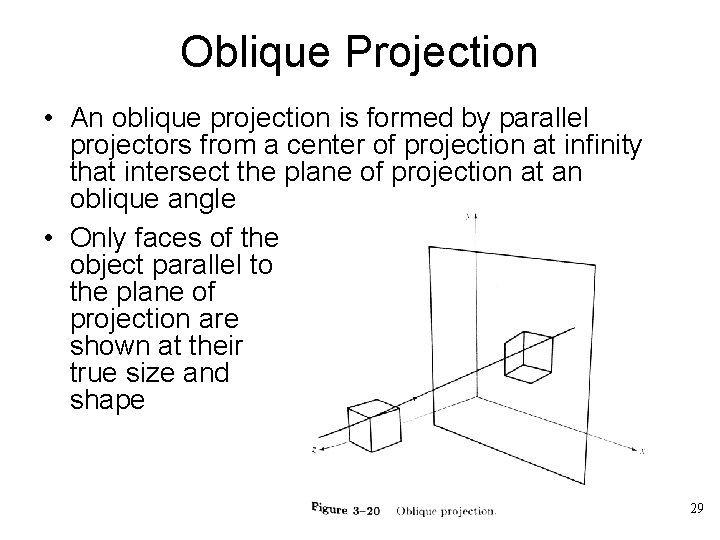
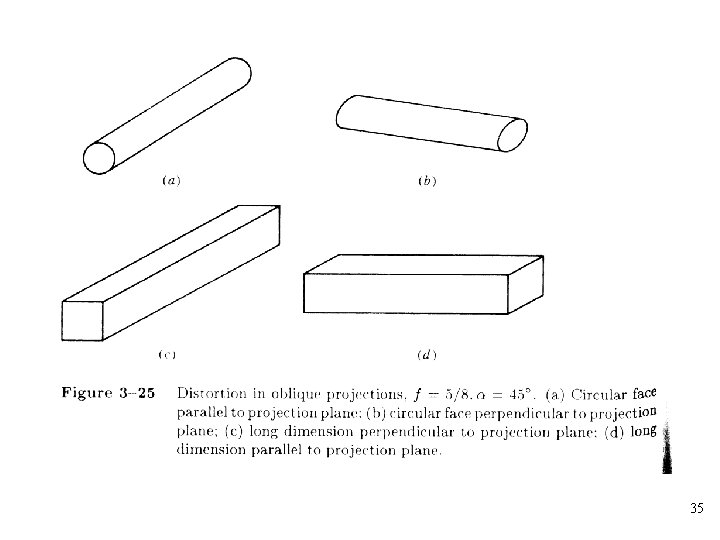
Oblique Projection • An oblique projection is formed by parallel projectors from a center of projection at infinity that intersect the plane of projection at an oblique angle • Only faces of the object parallel to the plane of projection are shown at their true size and shape 29

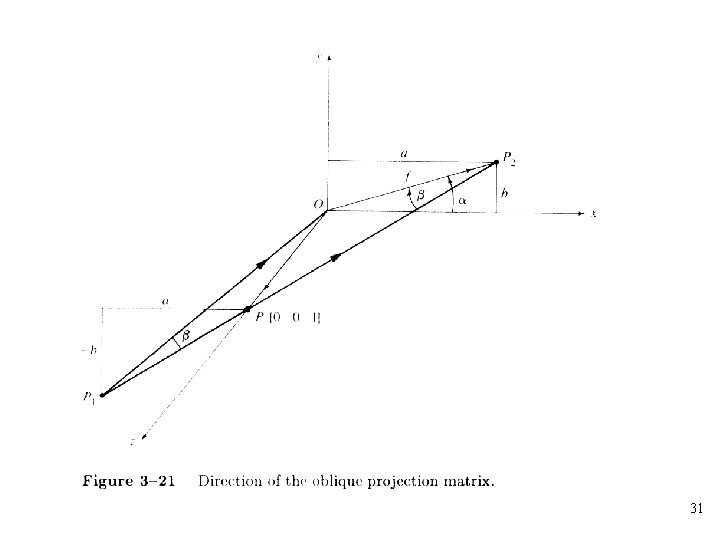
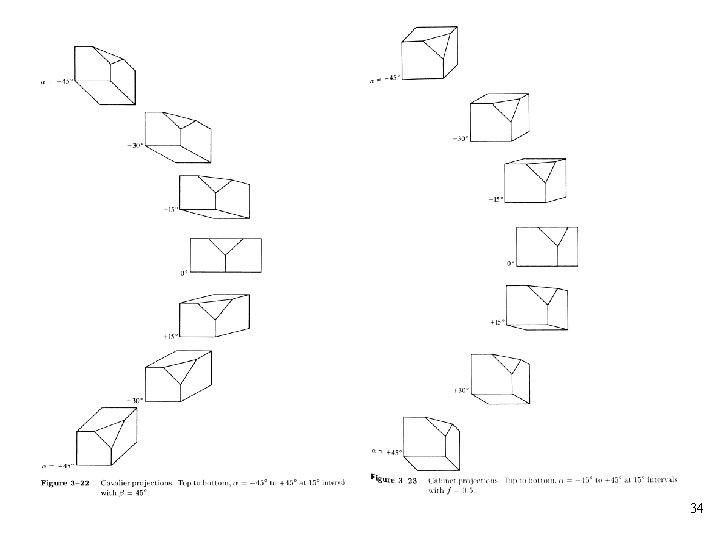
• Cavalier projection: The angle between the oblique projectors and the plane of projection is. The foreshortening factors for all three principal directions are equal to 1 • Cabinet projection: The foreshortening factor for edges perpendicular to the plane of projection is one-half. The angle between the projectors and the plane of projection is • The angle between the oblique projectors and the plane of projection is • The transformation for an oblique projector is 30

31

32

33

34

35

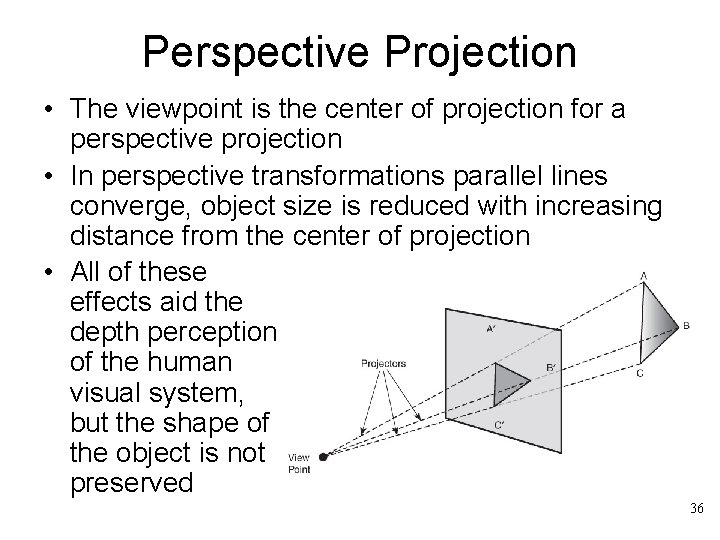
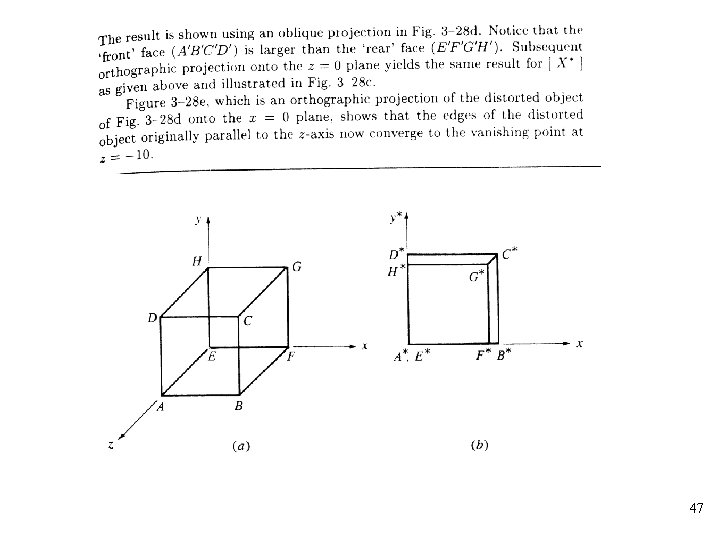
Perspective Projection • The viewpoint is the center of projection for a perspective projection • In perspective transformations parallel lines converge, object size is reduced with increasing distance from the center of projection • All of these effects aid the depth perception of the human visual system, but the shape of the object is not preserved 36

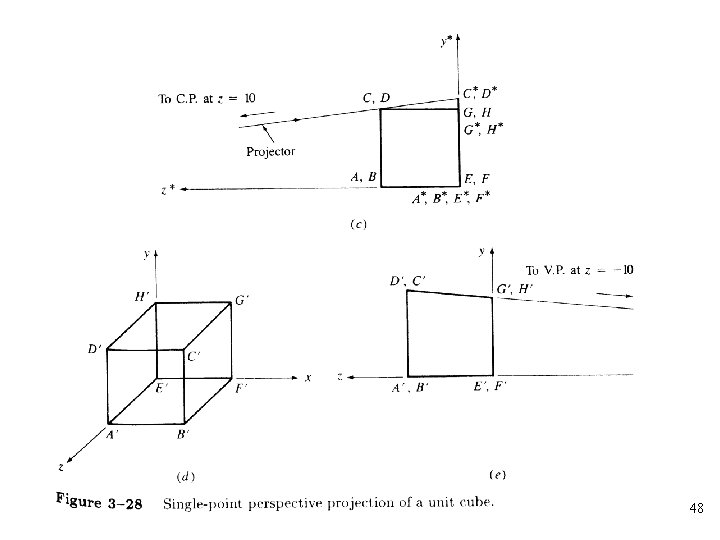
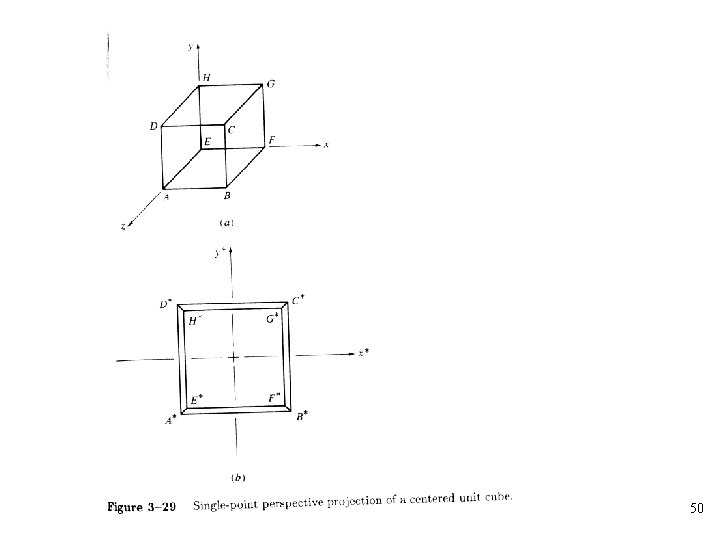
• Any of the first three elements of the fourth column of the general homogeneous coordinate transformation matrix is nonzero • The single-point perspective transformation with centers of projection and vanishing points on the z-axis: 37

38

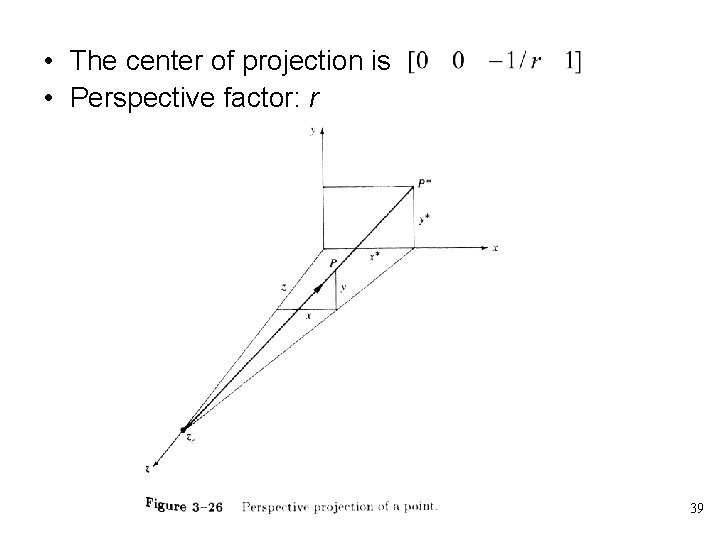
• The center of projection is • Perspective factor: r 39

40

41

• • Vanishing point : 42

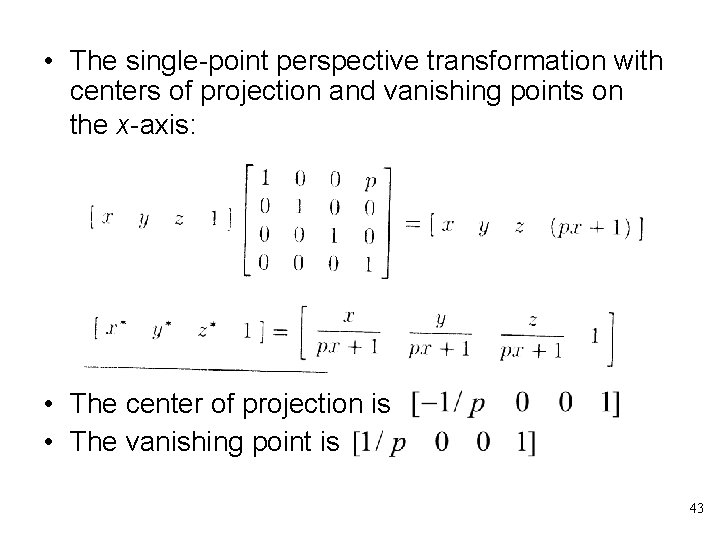
• The single-point perspective transformation with centers of projection and vanishing points on the x-axis: • The center of projection is • The vanishing point is 43

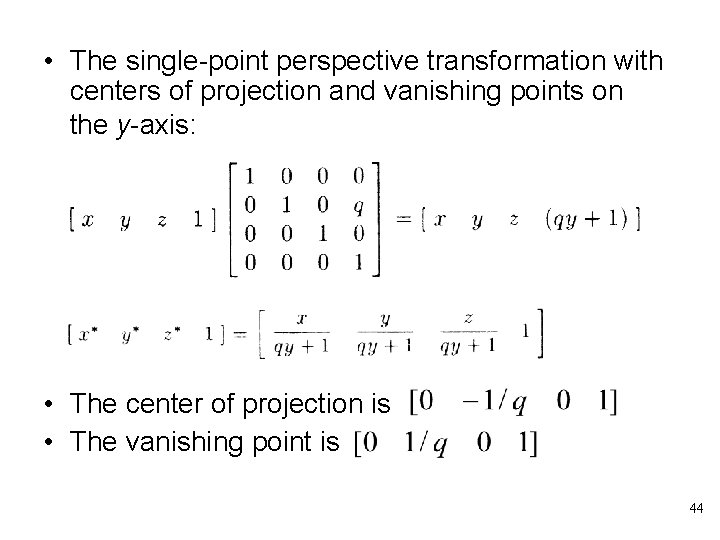
• The single-point perspective transformation with centers of projection and vanishing points on the y-axis: • The center of projection is • The vanishing point is 44

45

46

47

48

49

50

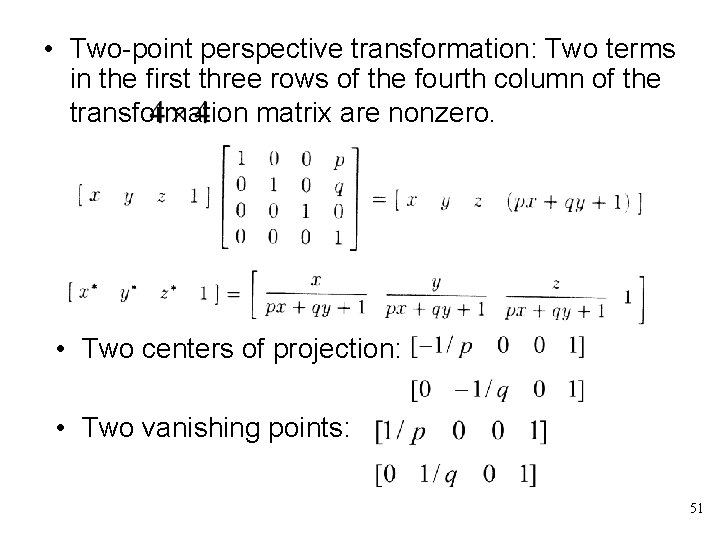
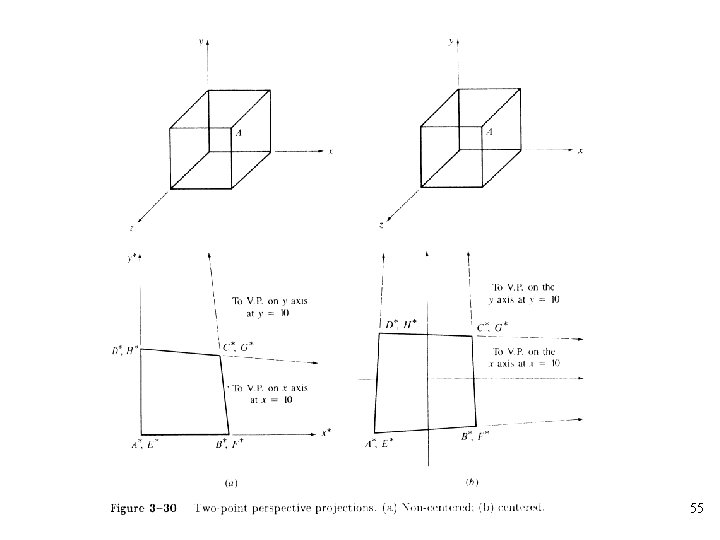
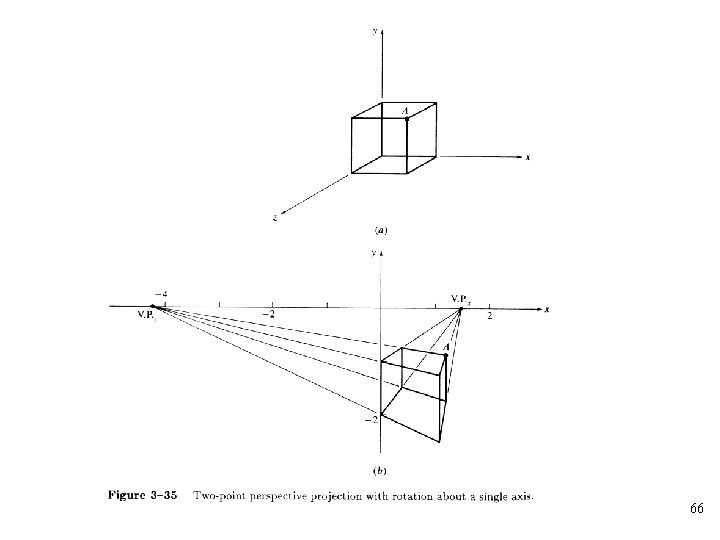
• Two-point perspective transformation: Two terms in the first three rows of the fourth column of the transformation matrix are nonzero. • Two centers of projection: • Two vanishing points: 51

52

53

54

55

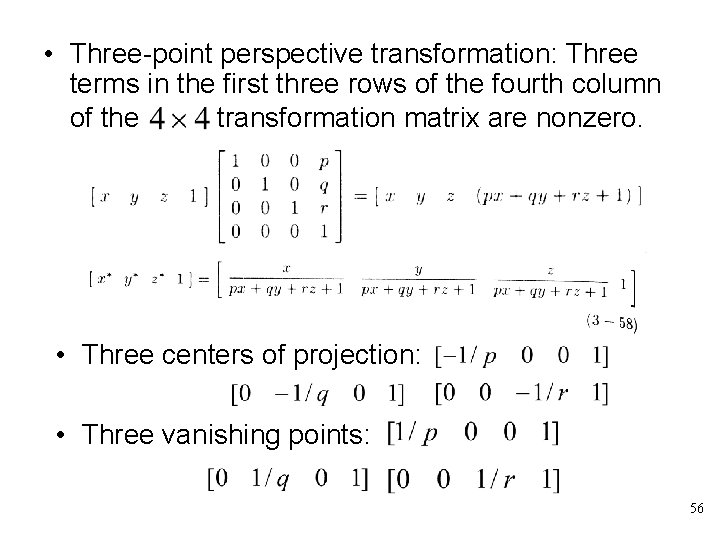
• Three-point perspective transformation: Three terms in the first three rows of the fourth column of the transformation matrix are nonzero. • Three centers of projection: • Three vanishing points: 56

57

58

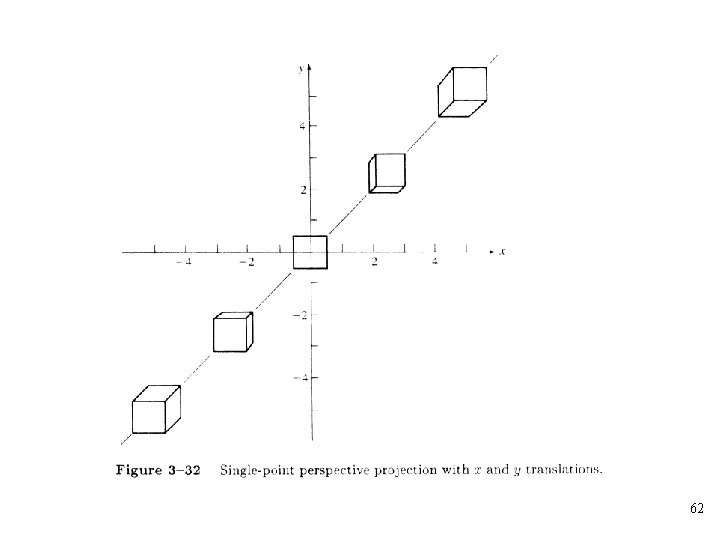
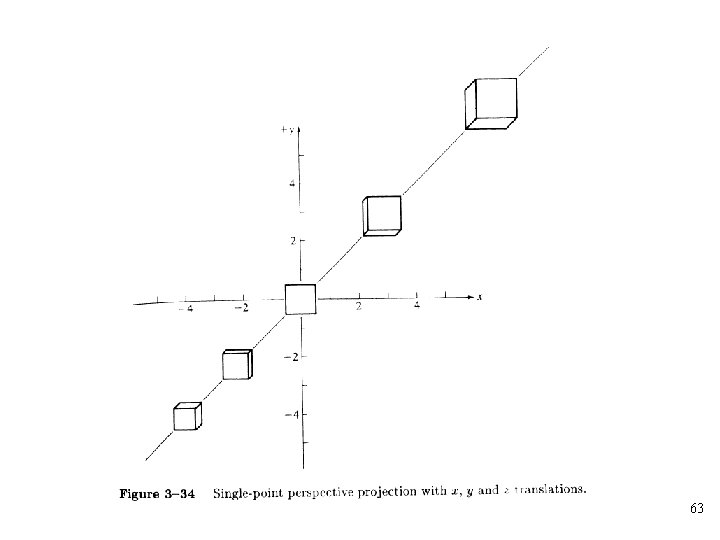
• Consider simple translation of the object followed by a single-point perspective projection from a center of projection at onto the z=0 plane 59

60

61

62

63

• Combine rotation and translation about a single principal axis to obtain an adequate 3 D representation 64

65

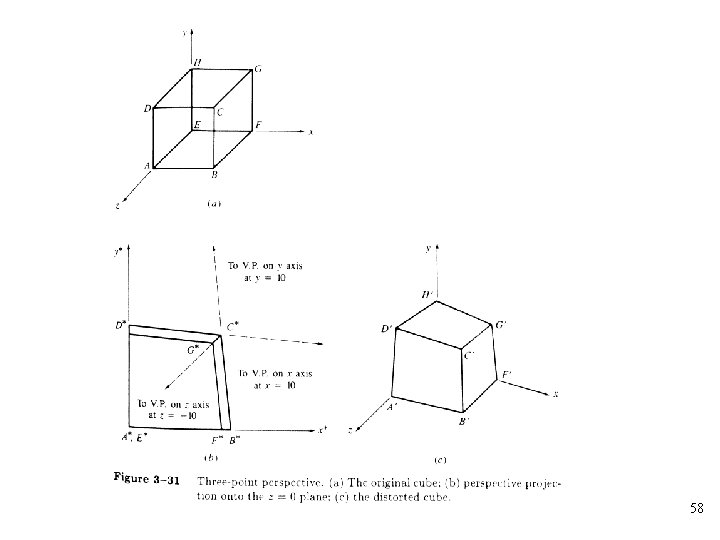
66

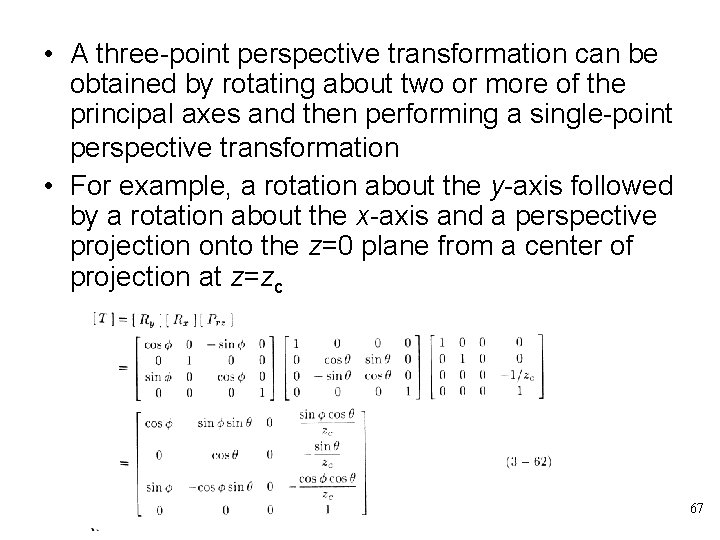
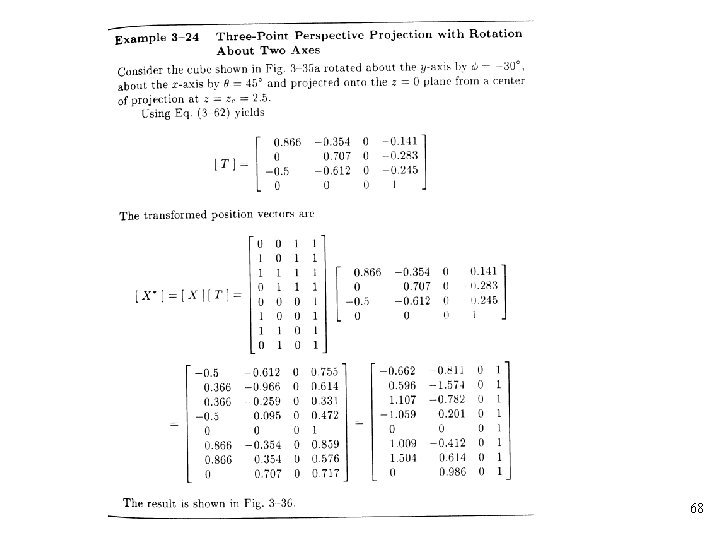
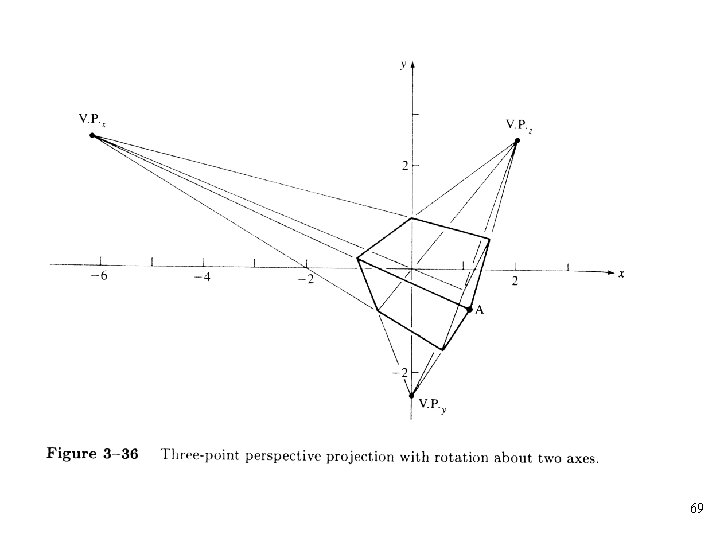
• A three-point perspective transformation can be obtained by rotating about two or more of the principal axes and then performing a single-point perspective transformation • For example, a rotation about the y-axis followed by a rotation about the x-axis and a perspective projection onto the z=0 plane from a center of projection at z=zc 67

68

69

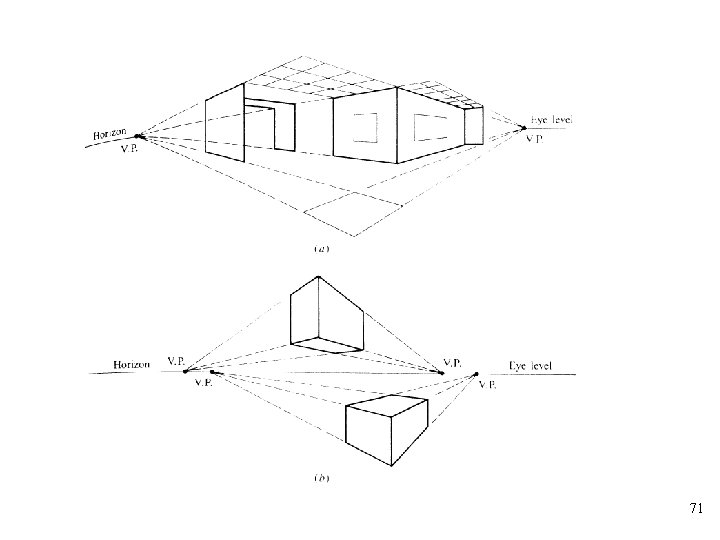
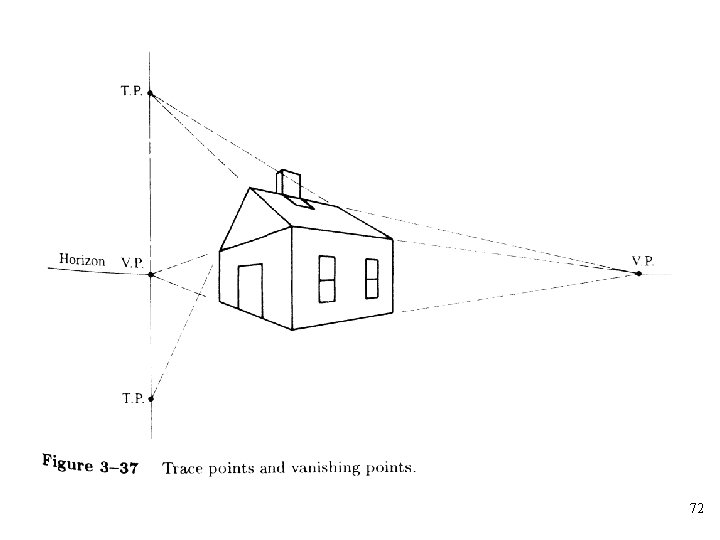
Vanishing Point • Principal vanishing points: Points on the horizontal reference line at which lines originally parallel to the untransformed principal axes converge, when a perspective view of an object is created by using a horizontal reference line, normally at eye level. • In general, different sets of parallel lines have different principal vanishing points • Trace points: For planes of an object which are tilted relative to the untransformed principal axes, the vanishing points fall above or below the horizontal reference line. These are often called trace points. 70

71

72

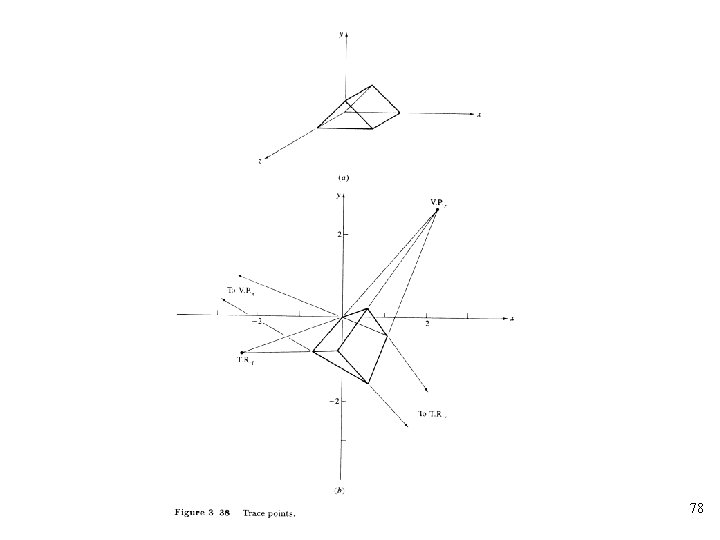
• The methods for determining the vanishing points: – The intersection point of a pair of transformed projected parallel lines 73

– The transformation of the points at infinity on the principal axes 74

• The transformation of the points at infinity for skew planes can be used to find trace point 75

76

77

78

Reconstruction of 3 D Images • The general perspective transformation is: • The transformation projected onto the z=0 plane is 79
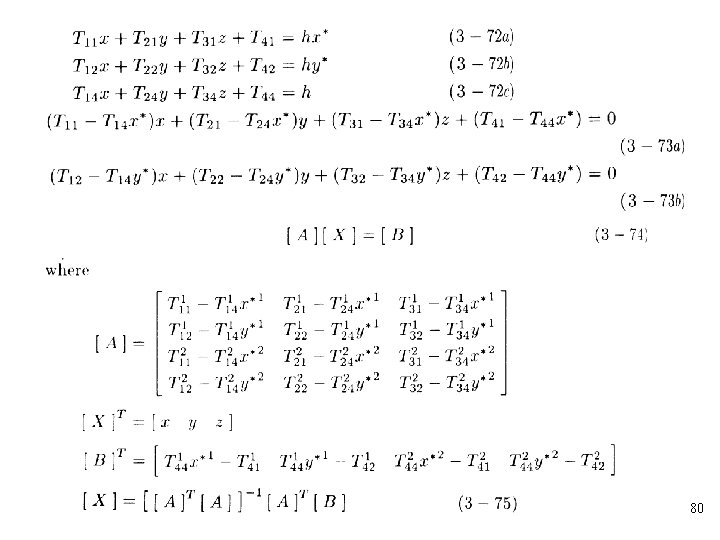
80

81

82

• If the location of several points which appear in the perspective projection are known in object space and in the perspective projection, then it is possible to determine the transformation elements 83

84

85

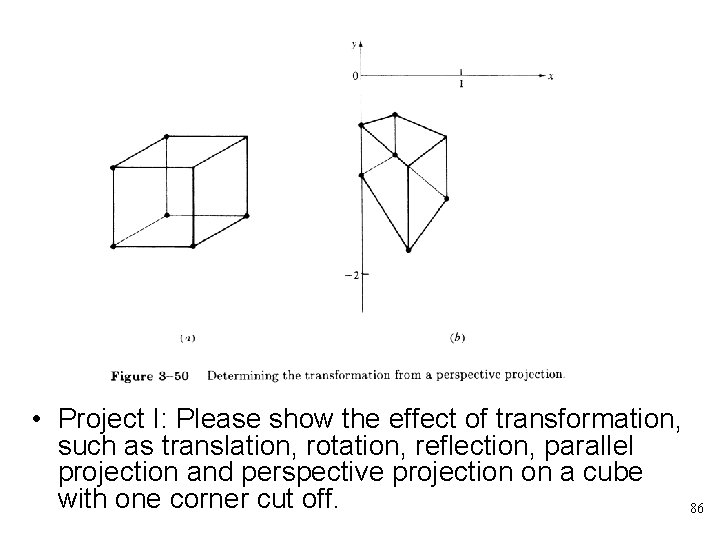
• Project I: Please show the effect of transformation, such as translation, rotation, reflection, parallel projection and perspective projection on a cube with one corner cut off. 86
 Projection matrix
Projection matrix Isometric drawing with orthographic view
Isometric drawing with orthographic view First and third angle projections
First and third angle projections Cavalier projection drawing
Cavalier projection drawing Scalar and vector projections
Scalar and vector projections Dnt
Dnt The hobbit orcs
The hobbit orcs Othello act three summary
Othello act three summary In three minutes write three things
In three minutes write three things Orange diamond-shaped signs warn the motorist of
Orange diamond-shaped signs warn the motorist of The three colonial sections-one society or three
The three colonial sections-one society or three Three address statement
Three address statement A bear searching for food wanders 35 meters east
A bear searching for food wanders 35 meters east Collinear vectors example
Collinear vectors example Carl yaztremski
Carl yaztremski A skater moves with 15 m/s in a circle
A skater moves with 15 m/s in a circle Heat always moves from
Heat always moves from Martin luther king jr s timeline
Martin luther king jr s timeline Digestive system helpers
Digestive system helpers A transition analysis can account for multiple moves.
A transition analysis can account for multiple moves. Moving learning games forward
Moving learning games forward A roller coaster moves 85m horizontally
A roller coaster moves 85m horizontally In the position shown collar b moves to the left
In the position shown collar b moves to the left We live in planet earth
We live in planet earth Outline of photosynthesis
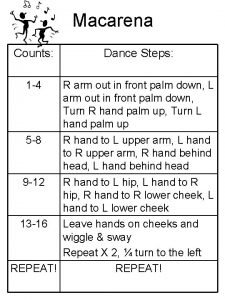
Outline of photosynthesis Cupid shuffle dance steps
Cupid shuffle dance steps Talk moves sentence starters
Talk moves sentence starters How does heat move
How does heat move Heat moves from
Heat moves from Earth's thickest layer
Earth's thickest layer Dogs bark caravan moves on
Dogs bark caravan moves on What are craft moves
What are craft moves America moves toward war
America moves toward war Oceans
Oceans A skater moves with 15 m/s in a circle
A skater moves with 15 m/s in a circle Carbon moves from the atmosphere to plants
Carbon moves from the atmosphere to plants Chapter 24 section 4 america moves toward war
Chapter 24 section 4 america moves toward war A sled moves on essentially frictionless ice
A sled moves on essentially frictionless ice It moves materials around to other parts of the cell
It moves materials around to other parts of the cell How helicopter moves forward
How helicopter moves forward The variable describes how quickly something moves
The variable describes how quickly something moves Marriage is a private affair summary in english
Marriage is a private affair summary in english Inductive reasoning
Inductive reasoning Speed is the ratio of the distance an object moves to *
Speed is the ratio of the distance an object moves to * Everything that lives and moves will be food for you
Everything that lives and moves will be food for you Chicken wing dissection lab answers
Chicken wing dissection lab answers America moves to the city chapter 25
America moves to the city chapter 25 It moves materials around to other parts of the cell
It moves materials around to other parts of the cell A cross country skier moves from location a to location b
A cross country skier moves from location a to location b A pet store supply truck moves at 25 m/s
A pet store supply truck moves at 25 m/s Vectors and scalars in physics
Vectors and scalars in physics A storm system moves 5000 km due east
A storm system moves 5000 km due east A bear searching for food wanders 35 meters east
A bear searching for food wanders 35 meters east Scanning lense
Scanning lense 8 thinking moves
8 thinking moves They say i say moves that matter in academic writing
They say i say moves that matter in academic writing Disco fingers
Disco fingers If car a passes car b, then car a must be
If car a passes car b, then car a must be History of the microscope
History of the microscope Legal moves for simplifying and comparing expressions
Legal moves for simplifying and comparing expressions A perennial mass of ice which moves over land
A perennial mass of ice which moves over land Which machine moves like a millipede
Which machine moves like a millipede Chapter 25 america moves to the city
Chapter 25 america moves to the city A square conductor moves through a uniform magnetic field
A square conductor moves through a uniform magnetic field Gtg stands for in automata
Gtg stands for in automata Parts of janssen microscope
Parts of janssen microscope Moves the stage slightly to sharpen the image
Moves the stage slightly to sharpen the image Moves the stage slightly to sharpen the image
Moves the stage slightly to sharpen the image A stiff bar that moves about a fixed point is a
A stiff bar that moves about a fixed point is a Current moves from
Current moves from What is the value of g on planet exidor?
What is the value of g on planet exidor? America moves to the city
America moves to the city Axial movements meaning
Axial movements meaning Junior achievement money moves song
Junior achievement money moves song Something that moves
Something that moves Language focus
Language focus A young couple moves into a new neighborhood
A young couple moves into a new neighborhood The cycling of materials
The cycling of materials Moves the stage slightly to sharpen the image.
Moves the stage slightly to sharpen the image. Chess pieces movements
Chess pieces movements S'cool moves i can calm myself
S'cool moves i can calm myself Camera moves
Camera moves A particle with a positive charge moves in the xz plane
A particle with a positive charge moves in the xz plane When a charged particle moves in a region of magnetic field
When a charged particle moves in a region of magnetic field A duck flying due east passes over atlanta
A duck flying due east passes over atlanta Inductive reasoning moves from general to specific
Inductive reasoning moves from general to specific Legal moves algebra tiles
Legal moves algebra tiles