Electric currents Static Electricity Static electricity is when

Electric currents

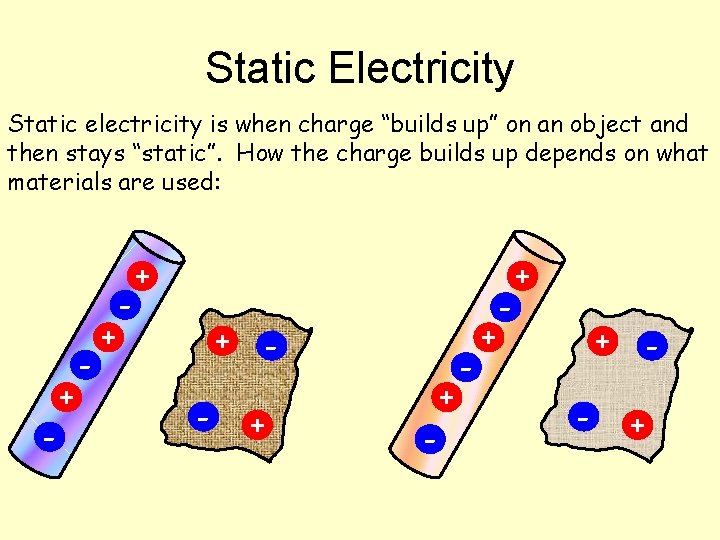
Static Electricity Static electricity is when charge “builds up” on an object and then stays “static”. How the charge builds up depends on what materials are used: - + - + - +

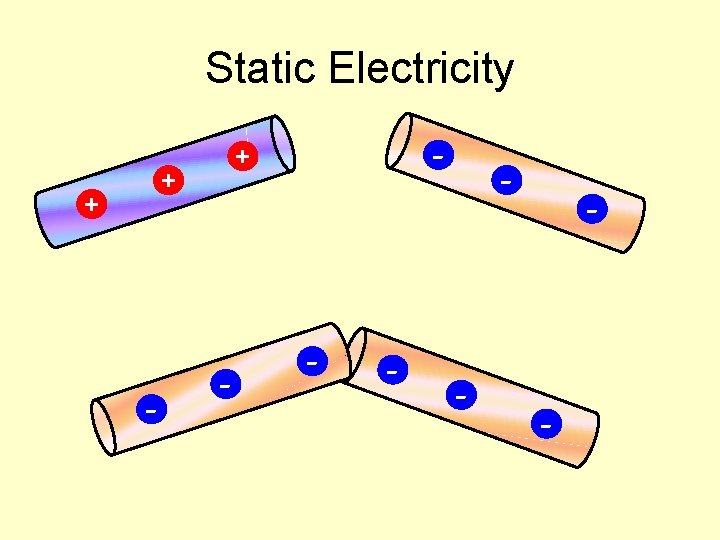
Static Electricity + + - - - - -

Static shock

Measuring Charge The charge on an electron is very small, so we measure charge using units called “coulombs” (C). One electron has a charge of 1. 6 x 10 -19 C. Charge can be measured using a coulombmeter, and they usually measure in nanocoloumbs (1 n. C = 10 -9 C). For example, a charged polythene rod may carry a charge of a few hundred nanocoulombs

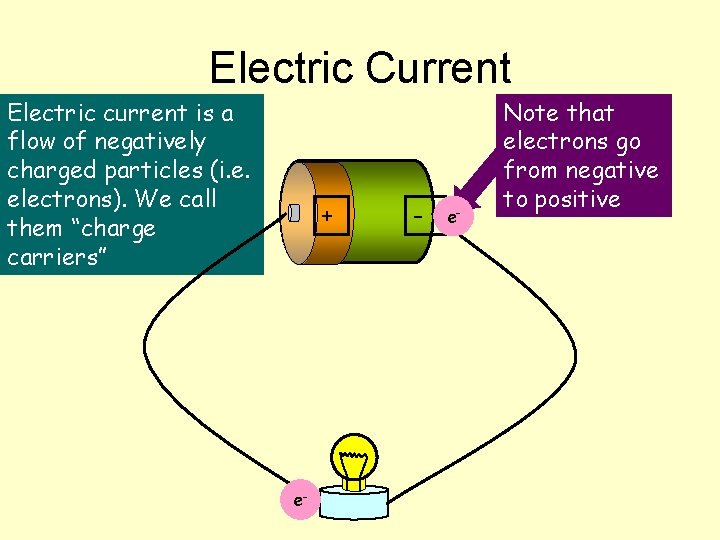
Electric Current Electric current is a flow of negatively charged particles (i. e. electrons). We call them “charge carriers” + e- - e- Note that electrons go from negative to positive

Define electric current. It is sufficient for students to know that current is defined in terms of the force per unit length between parallel current -carrying conductors.

Answers

Calculating Charge (Q) By definition, current is the rate of flow of charge. In other words, its how much charge flows per second. One amp (1 A) is equal to one coulomb per second (1 Cs-1). Charge and current are related by the equation: Current = rate of flow of charge I = Δq Δt 1. A battery supplies 10 C over a period of 50 seconds. What is the current? 2. Another battery is connected for 2 minutes and provided a current of 0. 4 A. How much charge flowed? 3. A car battery has a capacity of 24 Ah (amp hours). If it provides a current of 48 A how long can it be used for? How much charge (in coulombs) does it contain?

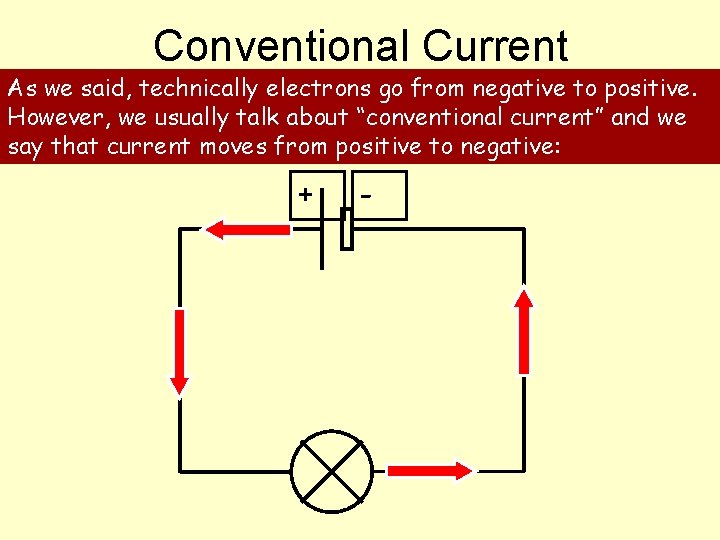
Conventional Current As we said, technically electrons go from negative to positive. However, we usually talk about “conventional current” and we say that current moves from positive to negative: + -

How long will it take for the electrons to complete 1 circuit?

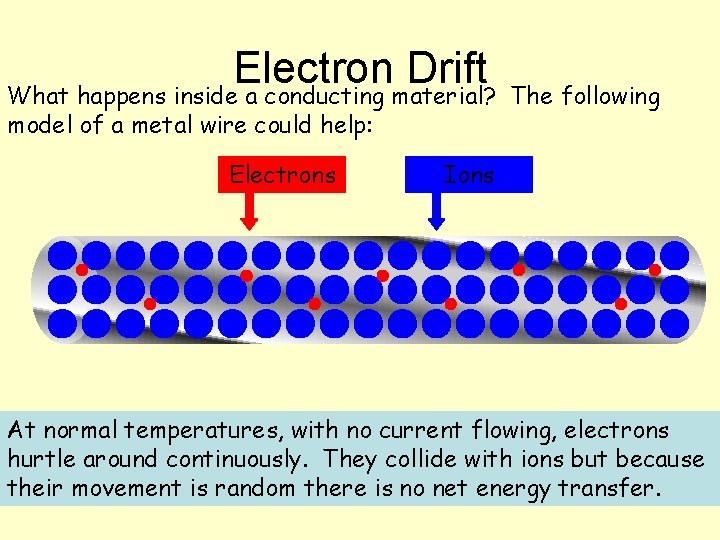
Electron Drift What happens inside a conducting material? model of a metal wire could help: Electrons The following Ions At normal temperatures, with no current flowing, electrons hurtle around continuously. They collide with ions but because their movement is random there is no net energy transfer.

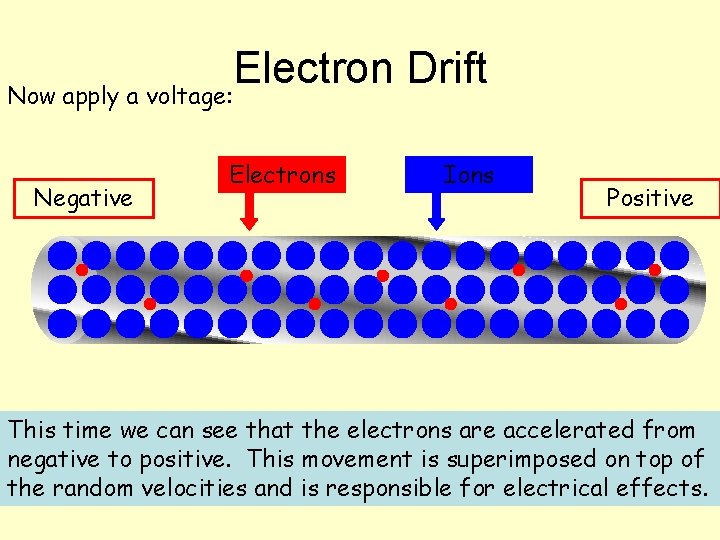
Electron Drift Now apply a voltage: Negative Electrons Ions Positive This time we can see that the electrons are accelerated from negative to positive. This movement is superimposed on top of the random velocities and is responsible for electrical effects.

What does an electric current look like? Download Run Now!

Conductors…. . How many free electrons?

Hyperlink

Basic ideas… Electric current is when electrons start to flow around a circuit. We use an _____ to measure it and it is measured in ____. Potential difference (also called _______) is how big the push on the electrons is. We use a ____ to measure it and it is measured in ______, a unit named after Volta. Resistance is anything that resists an electric current. It is measured in _____. Words: volts, amps, ohms, voltage, ammeter, voltmeter

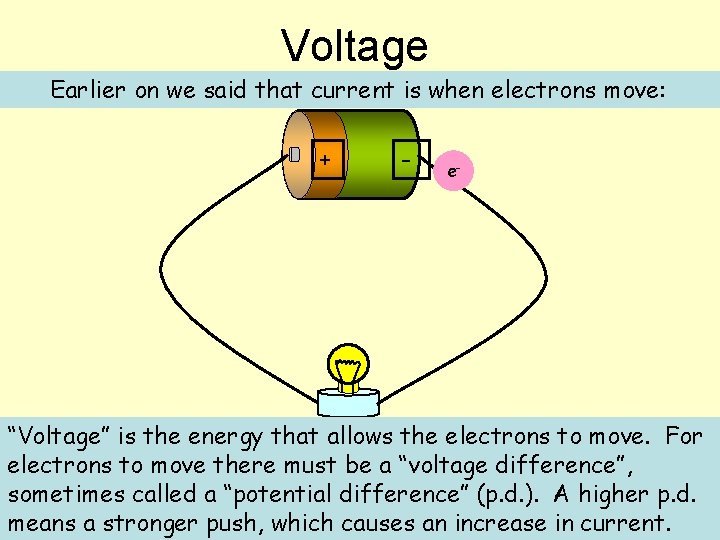
Voltage Earlier on we said that current is when electrons move: + - e- “Voltage” is the energy that allows the electrons to move. For e electrons to move there must be a “voltage difference”, sometimes called a “potential difference” (p. d. ). A higher p. d. means a stronger push, which causes an increase in current.

Define electric potential difference The potential difference between 2 points in a circuit is……. . (1 volt = 1 joule per coulomb)

Resistance is anything that will RESIST a current. It is measured in Ohms, a unit named after me. Define resistance. Students should be aware that R = V/I is a general definition of resistance. It is not a statement of Ohm’s law. Students should understand what is meant by resistor. Georg Simon Ohm 1789 -1854 The resistance of a component can be calculated using Resistance (in ) = V Voltage (in V) Current (in A) I R

Resistance is anything that opposes an electric current. Resistance (Ohms, ) = Potential Difference (volts, V) Current (amps, A) What is the resistance of the following: 1) A bulb with a voltage of 3 V and a current of 1 A. 2) A resistor with a voltage of 12 V and a current of 3 A 3) A diode with a voltage of 240 V and a current of 40 A 4) A thermistor with a current of 0. 5 A and a voltage of 10 V

Resistivity Apply the equation for resistance in the form where ρ is the resistivity of the material of the resistor. What effect does doubling the diameter have on the resistance?

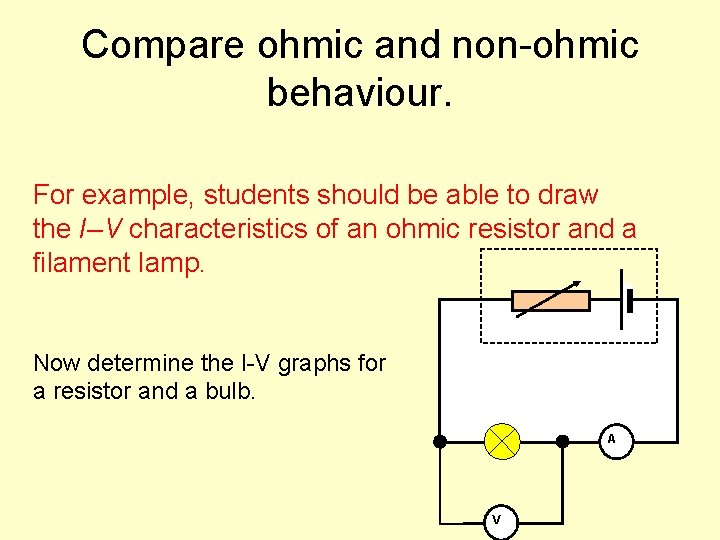
Compare ohmic and non-ohmic behaviour. For example, students should be able to draw the I–V characteristics of an ohmic resistor and a filament lamp. Now determine the I-V graphs for a resistor and a bulb. A V

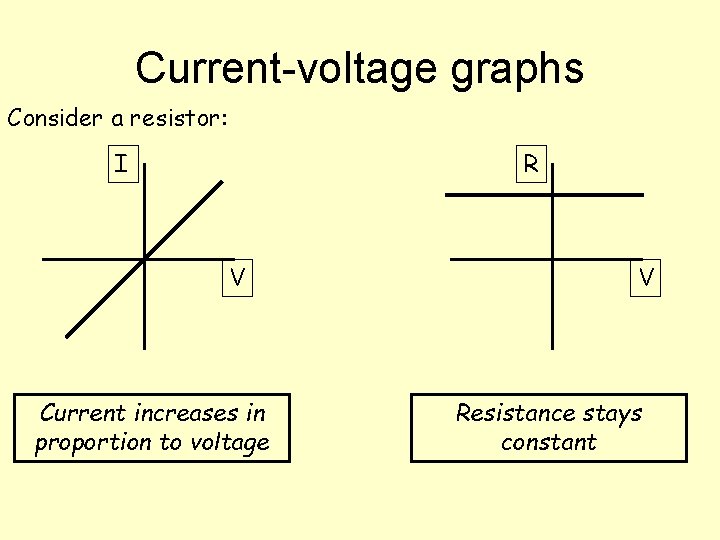
Current-voltage graphs Consider a resistor: I R V Current increases in proportion to voltage V Resistance stays constant

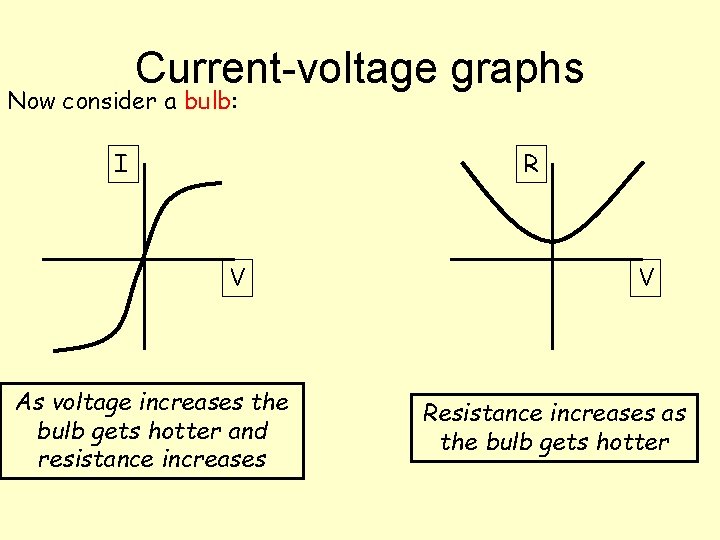
Current-voltage graphs Now consider a bulb: I R V As voltage increases the bulb gets hotter and resistance increases V Resistance increases as the bulb gets hotter

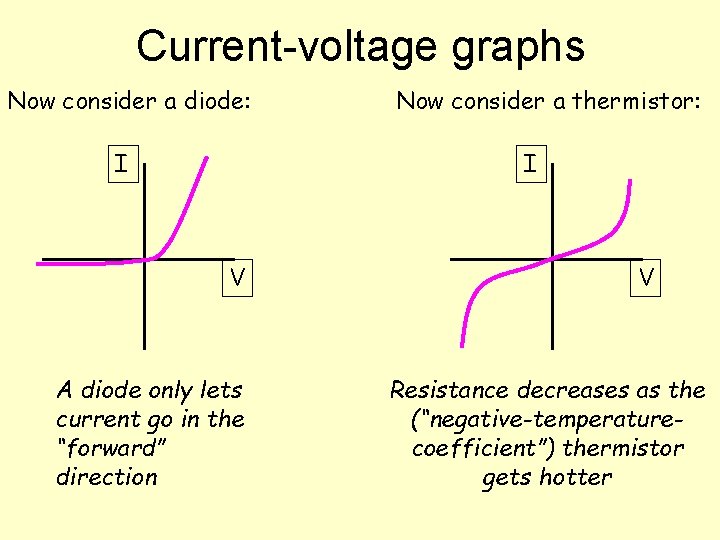
Current-voltage graphs Now consider a diode: I Now consider a thermistor: I V A diode only lets current go in the “forward” direction V Resistance decreases as the (“negative-temperaturecoefficient”) thermistor gets hotter

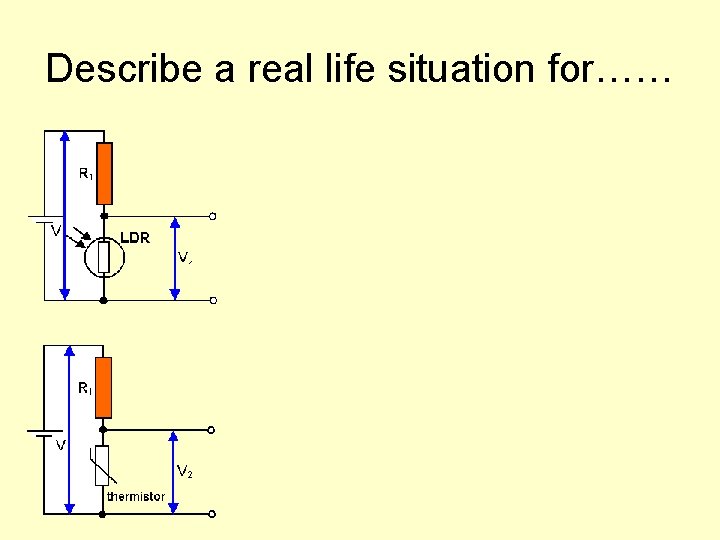
LDR and Thermistor How does their resistance vary with light and heat?

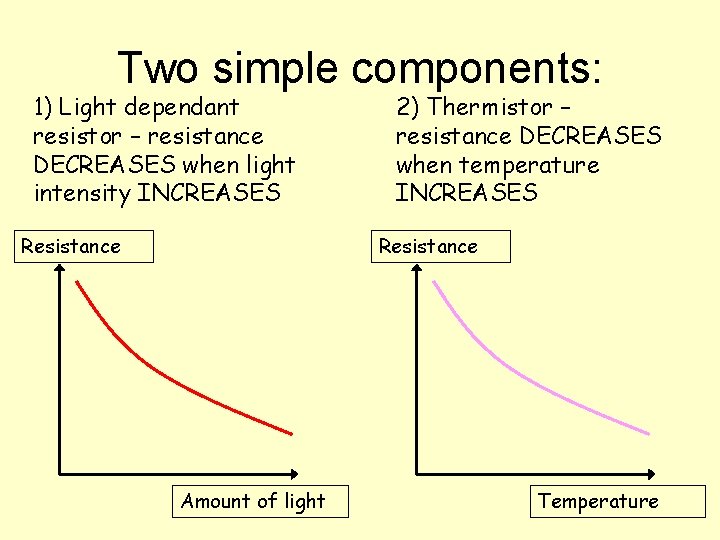
Two simple components: 1) Light dependant resistor – resistance DECREASES when light intensity INCREASES Resistance 2) Thermistor – resistance DECREASES when temperature INCREASES Resistance Amount of light Temperature

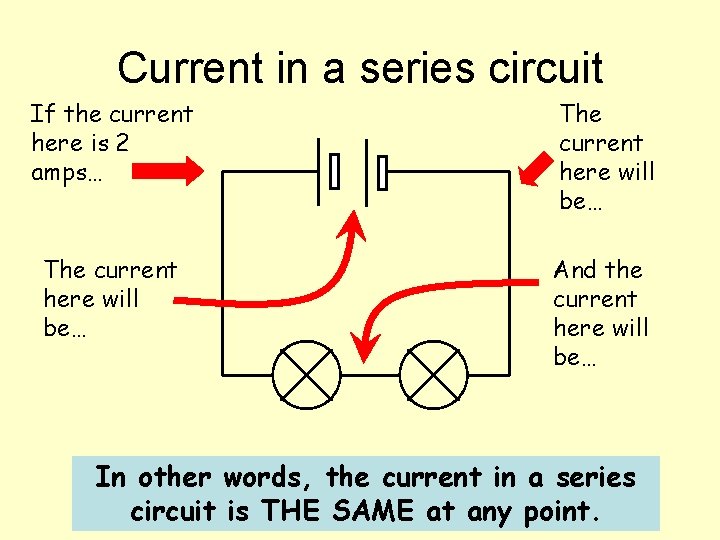
Current in a series circuit If the current here is 2 amps… The current here will be… And the current here will be… In other words, the current in a series circuit is THE SAME at any point.

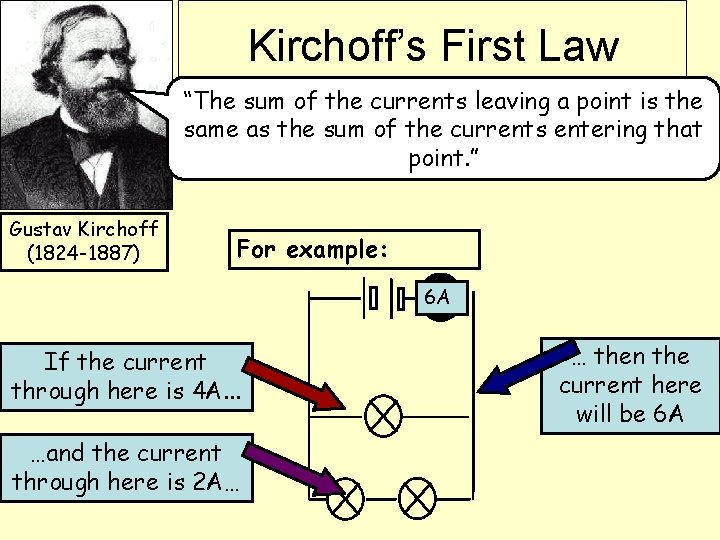
Kirchoff’s First Law “The sum of the currents leaving a point is the same as the sum of the currents entering that point. ” Gustav Kirchoff (1824 -1887) For example: 6 A If the current through here is 4 A. . . …and the current through here is 2 A… … then the current here will be 6 A

What happens if you have a choice?

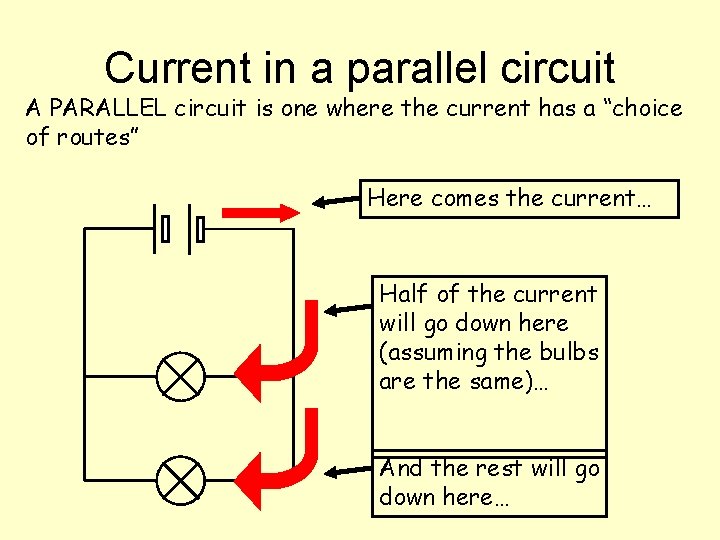
Current in a parallel circuit A PARALLEL circuit is one where the current has a “choice of routes” Here comes the current… Half of the current will go down here (assuming the bulbs are the same)… And the rest will go down here…

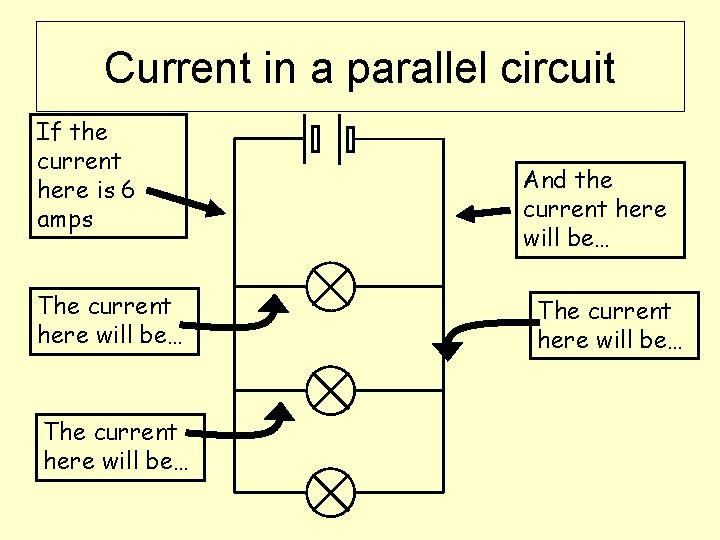
Current in a parallel circuit If the current here is 6 amps The current here will be… And the current here will be… The current here will be…

What is the current in each bulb? 3 A 6 A

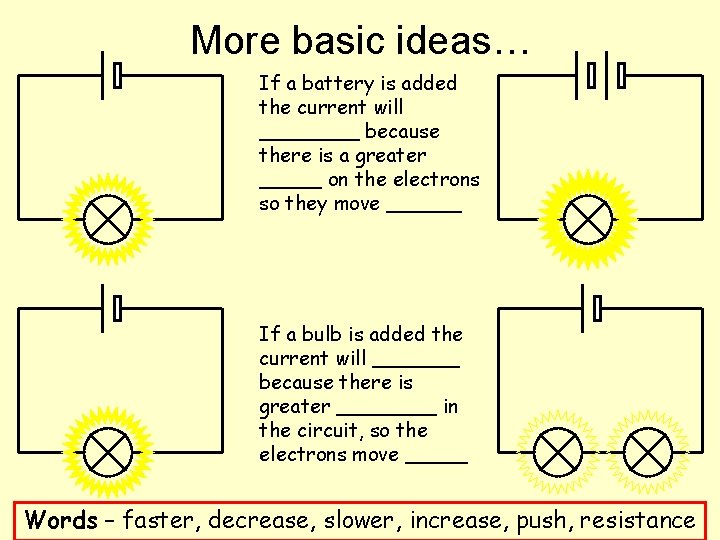
More basic ideas… If a battery is added the current will ____ because there is a greater _____ on the electrons so they move ______ If a bulb is added the current will _______ because there is greater ____ in the circuit, so the electrons move _____ Words – faster, decrease, slower, increase, push, resistance

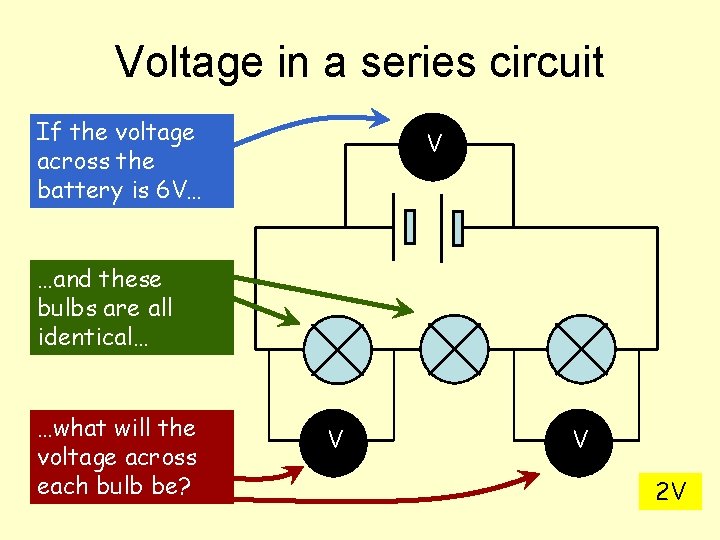
Voltage in a series circuit If the voltage across the battery is 6 V… V …and these bulbs are all identical… …what will the voltage across each bulb be? V V 2 V

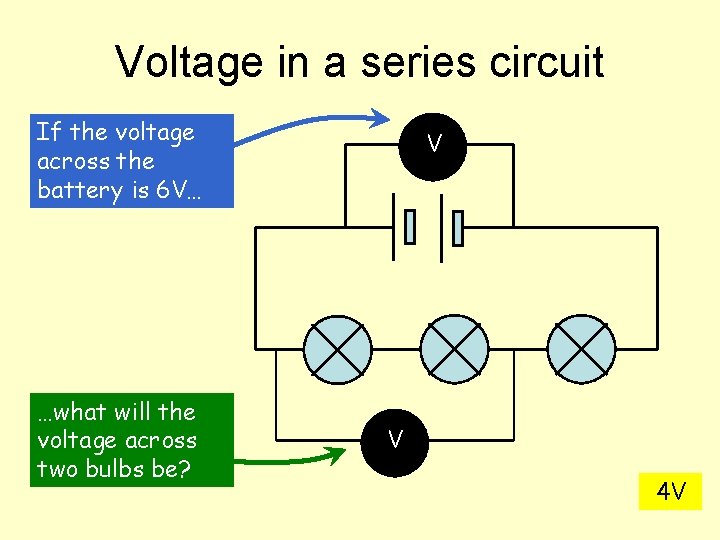
Voltage in a series circuit If the voltage across the battery is 6 V… …what will the voltage across two bulbs be? V V 4 V

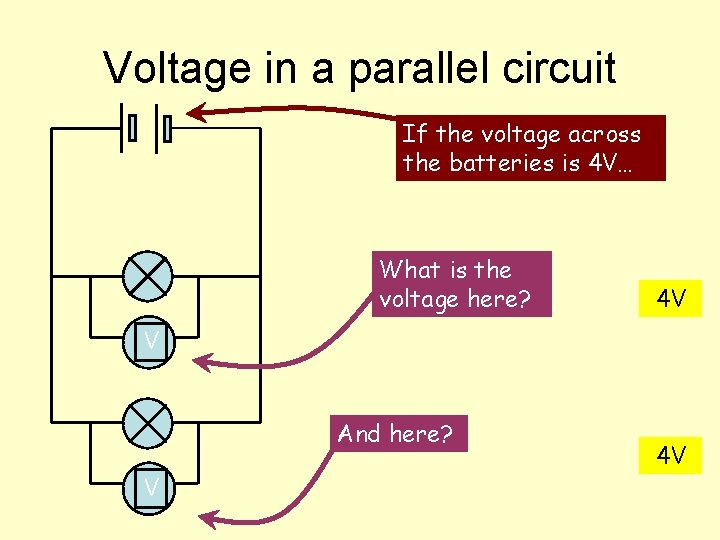
Voltage in a parallel circuit If the voltage across the batteries is 4 V… What is the voltage here? 4 V V And here? V 4 V

In a SERIES circuit: Summary Current is THE SAME at any point Voltage SPLITS UP over each component In a PARALLEL circuit: Current SPLITS UP down each “strand” Voltage is THE SAME across each”strand”

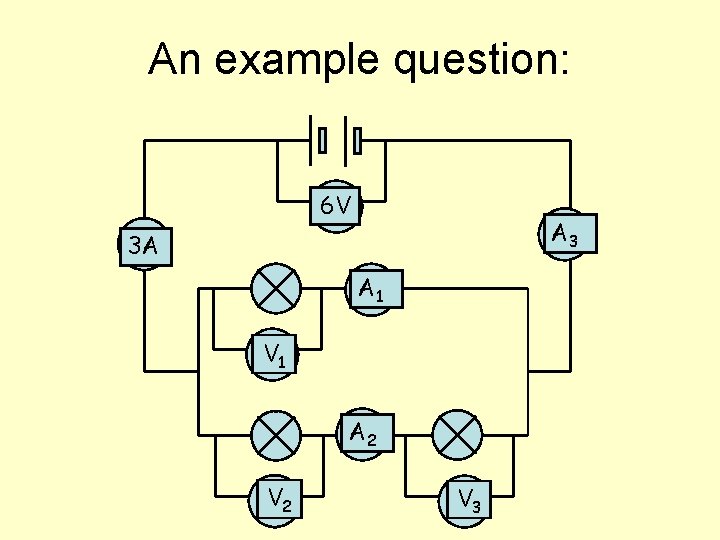
An example question: 6 V A 3 3 A A 1 V 1 A 2 V 3

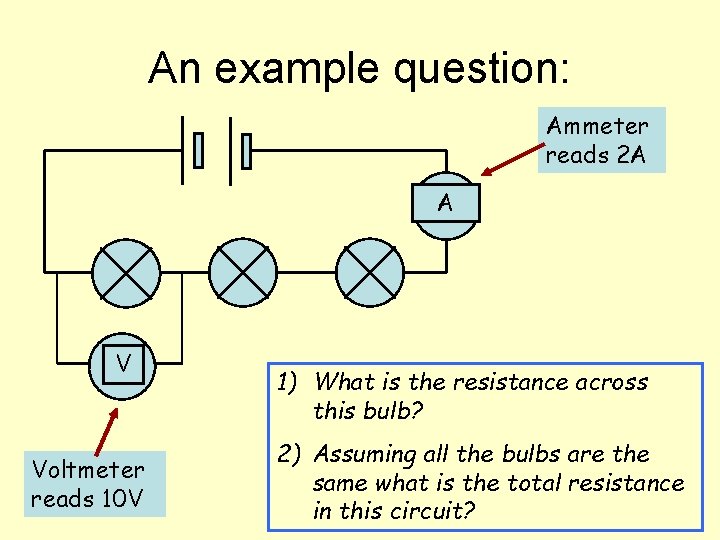
An example question: Ammeter reads 2 A A V Voltmeter reads 10 V 1) What is the resistance across this bulb? 2) Assuming all the bulbs are the same what is the total resistance in this circuit?

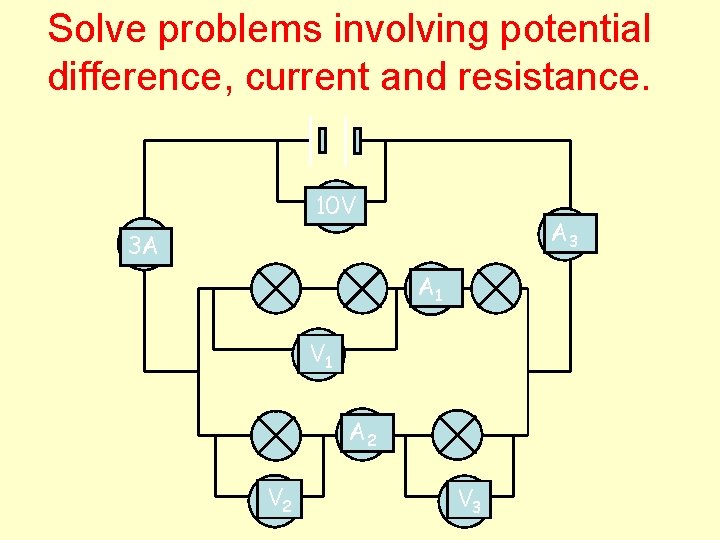
Solve problems involving potential difference, current and resistance. 10 V A 3 3 A A 1 V 1 A 2 V 3

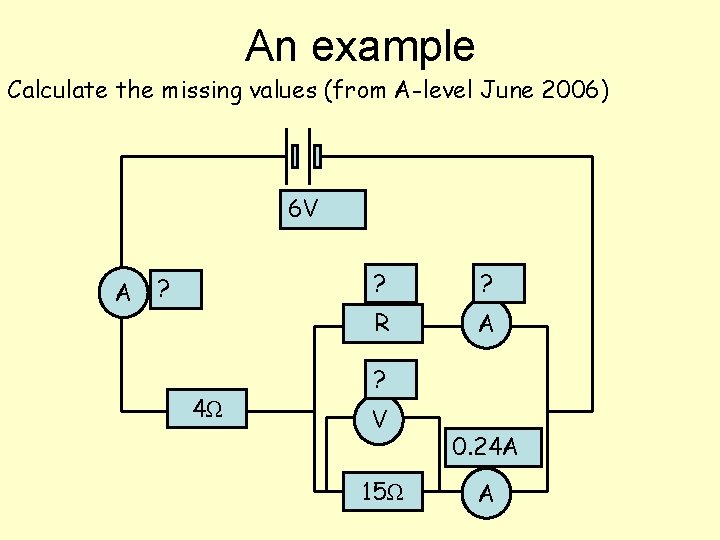
An example Calculate the missing values (from A-level June 2006) 6 V A ? 4Ω ? ? R A ? V 15Ω 0. 24 A A

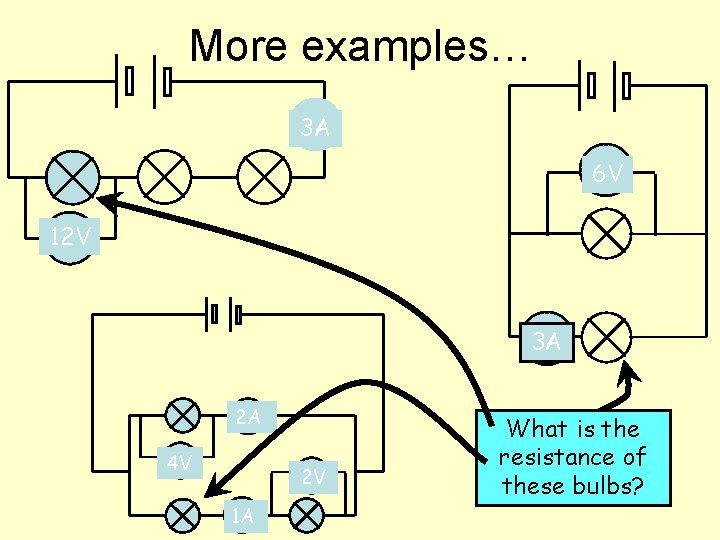
More examples… 3 A 6 V 12 V 3 A 2 A 4 V 2 V 1 A What is the resistance of these bulbs?

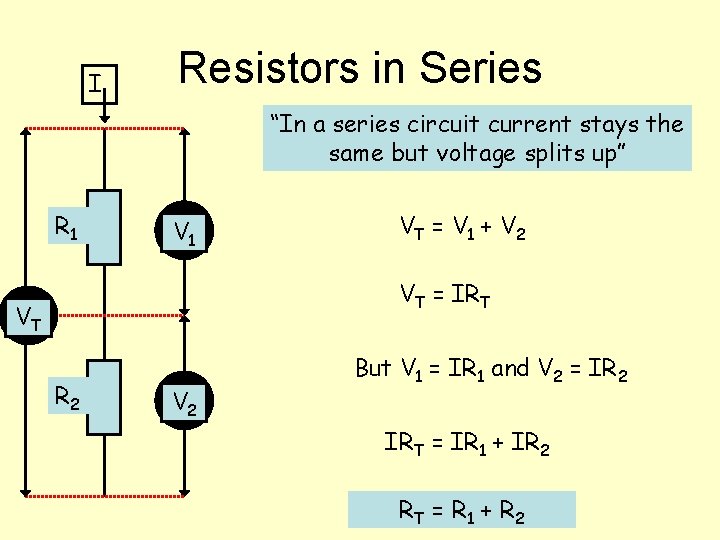
I Resistors in Series “In a series circuit current stays the same but voltage splits up” R 1 VT = V 1 + V 2 VT = IRT VT R 2 V 2 But V 1 = IR 1 and V 2 = IR 2 IRT = IR 1 + IR 2 RT = R 1 + R 2

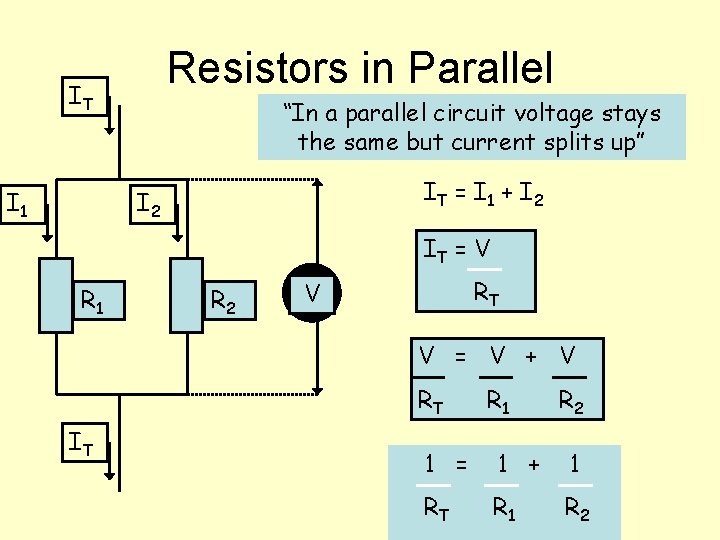
Resistors in Parallel IT I 1 “In a parallel circuit voltage stays the same but current splits up” IT = I 1 + I 2 IT = V R 1 R 2 RT V V = V + V RT IT R 1 R 2 1 = 1 + 1 RT R 1 R 2

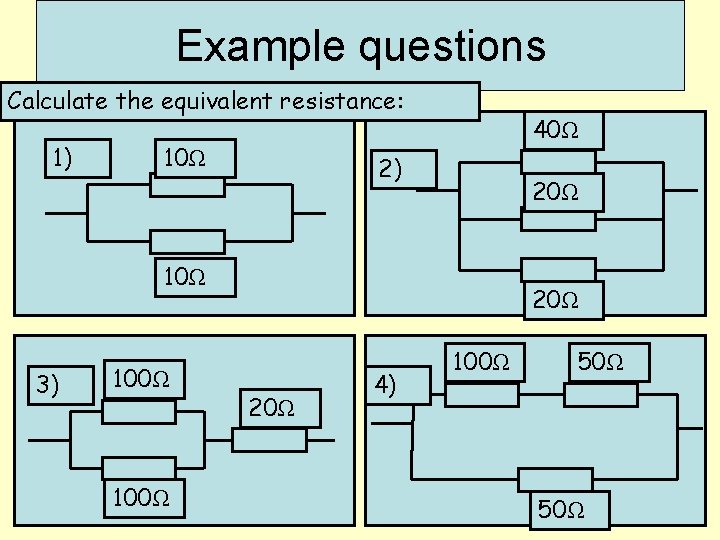
Example questions Calculate the equivalent resistance: 1) 10Ω 40Ω 2) 20Ω 10Ω 3) 100Ω 20Ω 4) 100Ω 50Ω

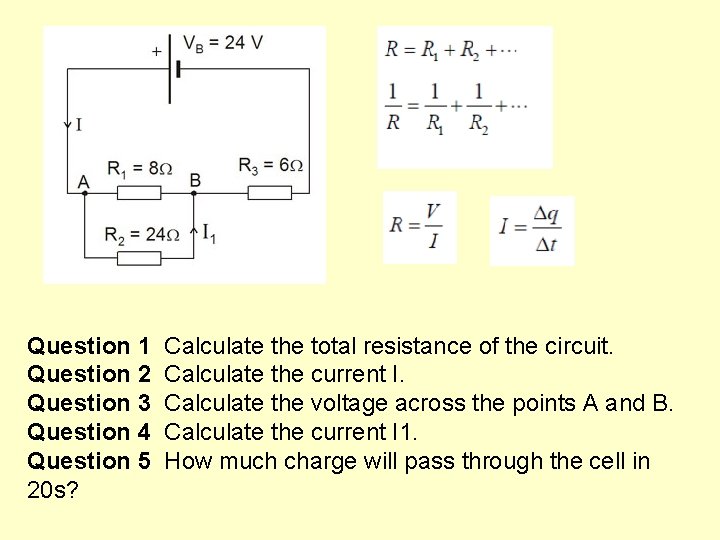
Question 1 Calculate the total resistance of the circuit. Question 2 Calculate the current I. Question 3 Calculate the voltage across the points A and B. Question 4 Calculate the current I 1. Question 5 How much charge will pass through the cell in 20 s?

Each of the resistors in the circuit below has a resistance R Ohms. What is their total resistance (in terms of R). Calculate the total resistance of the four resistors in the circuit shown below Calculate the total resistance of the same four resistors when a wire of very low resistance is connected across points X and Y.

Describe a real life situation for……

Describe the use of ideal ammeters and ideal voltmeters. Ideal ammeters have ……. resistance and are connected in …………. Ideal voltmeters have ……. resistance and are connected in ………….

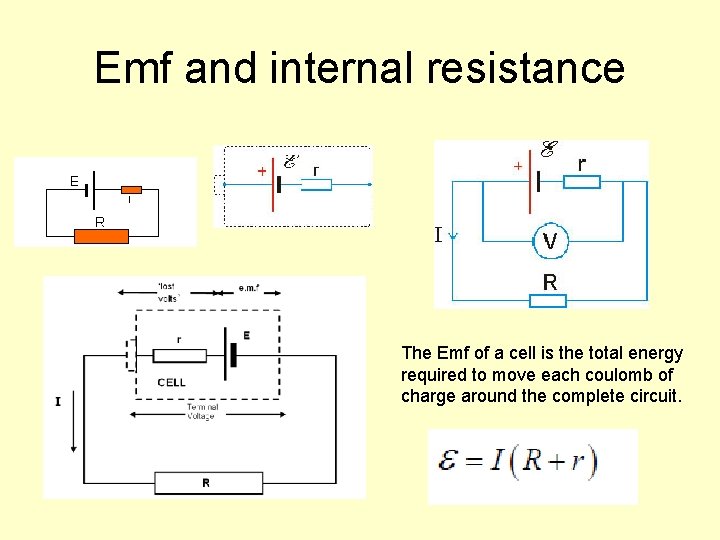
Emf and internal resistance The Emf of a cell is the total energy required to move each coulomb of charge around the complete circuit.

Measuring Emf and internal resistance Apparatus required: Cell Two multimeters (or an ammeter and voltmeter) Rheostat (approx. 20 Ω) Leads Circuit: A V Procedure Start with the rheostat on its maximum resistance. Record V and I. Gradually reduce the rheostat to its lowest resistance (zero) measuring V and I a minimum of 7 times over the range. Don’t leave the circuit connected for long when the resistance is low (current high) because this will run the cell down quickly. Plot a graph of V against I. Determine the Emf and r

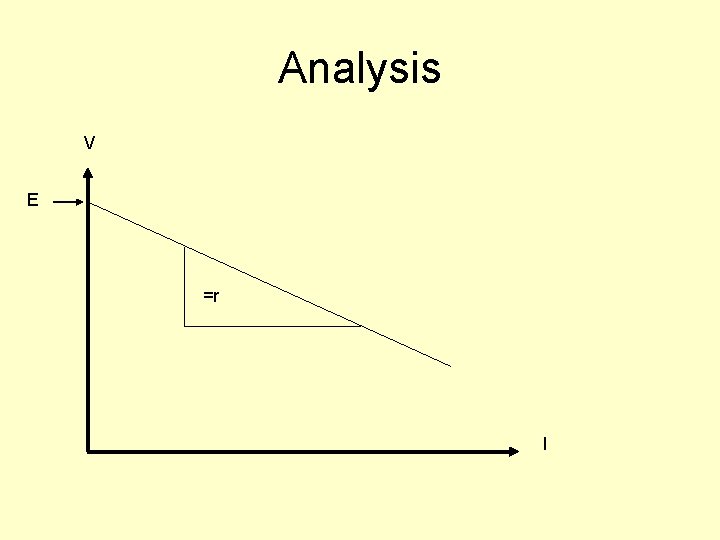
Analysis V E =r I

The electronvolt • What is an electronvolt? • What are the units of the electronvolt? • Why do we need to use the electronvolt? • How are electron beams produced? • How fast do electrons move in an electron beam?

Define the electronvolt Click to play

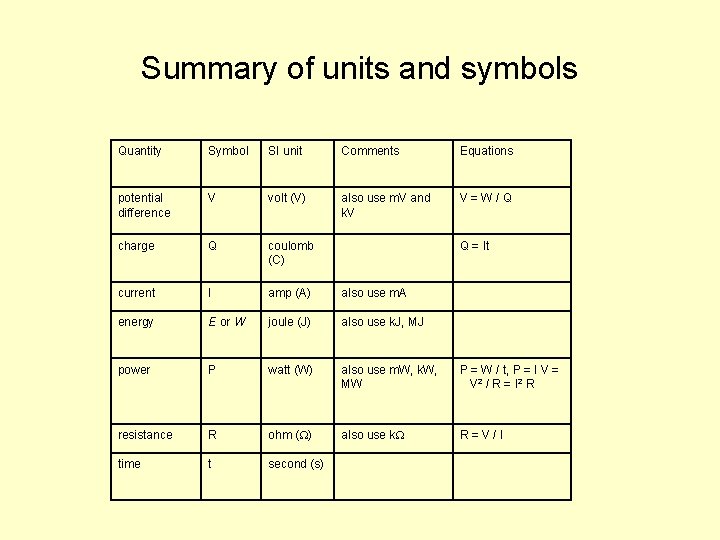
Summary of units and symbols Quantity Symbol SI unit Comments Equations potential difference V volt (V) also use m. V and k. V V = W / Q charge Q coulomb (C) Q = It current I amp (A) also use m. A energy E or W joule (J) also use k. J, MJ power P watt (W) also use m. W, k. W, MW P = W / t, P = I V = V 2 / R = I 2 R resistance R ohm ( ) also use k R = V / I time t second (s)