Isomorfismo Definio Dados dois espaos vetoriais reais e


















- Slides: 19

Isomorfismo Definição: Dados dois espaços vetoriais reais e uma transformação linear de entre eles. Dizemos que a transformação linear é um isomorfismo entre eles se é uma transformação bijetora (isto é, injetora e sobrejetora). Notação:

Automorfismo Definição: Dizemos que um isomorfismo entre espaços vetoriais reais é um automorfismo se os espaços são iguais, ou seja, T é um isomorfismo de um espaço nele mesmo. Proposição: Dado um isomorfismo sua transformação inversa é também um isomorfismo.

Resultados Importantes Proposição: Dados dois espaços vetoriais reais de mesma dimensão, então a transformação linear dada a seguir é um isomorfismo entre eles.

Resultados Importantes Teorema: Dois espaços vetoriais de dimensão finita são isomorfos se e somente se Exercícios: Transformações Lineares II

Operações com Transformações Lineares Definição: Dados dois espaços vetoriais reais, definimos o conjunto das transformações lineares entre eles por: Observação: Se os espaços vetoriais reais são iguais então

Operações com Transformações Lineares Adição: Dados dois elementos do conjunto das transformações lineares entre espaços vetoriais reais, definimos:

Propriedades da Adição P 1) Associativa P 2) Comutativa

Propriedades da Adição P 3) Elemento Neutro P 4) Elemento Oposto

Operações com Transformações Lineares Multiplicação por escalar: Denominamos de produto escalar de uma transformação linear à seguinte função:

Propriedades da Multiplicação por escalar P 1) P 2) P 3) P 4)

Novo Espaço Vetorial Das considerações anteriores temos um novo espaço vetorial real, com as operações de adição e multiplicação por escalar como definidas:

Operações com Transformações Lineares Composição: Dados dois elementos do conjunto dos operadores lineares, definimos a composição como sendo:

Propriedades da Composição P 1) Associativa P 2) Distributiva

Propriedades da Composição P 3) Elemento Neutro Obs: Em geral, a composição não é comutativa.

Operações com Transformações Lineares Potenciação: definimos a Potenciação por recorrência do seguinte modo:

Operadores Especiais Operador Idempotente: Operador Nilpotente:

Matriz de uma Transformação Linear Dados dois espaços vetoriais reais e uma transformação linear entre eles temos: Bases

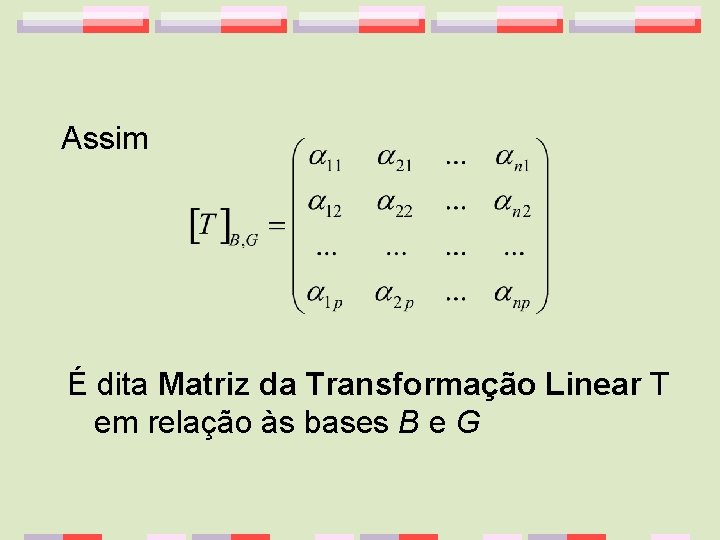
Assim É dita Matriz da Transformação Linear T em relação às bases B e G

Isomorfismo Especial Definição: Dados dois espaços vetoriais reais, com dimensões n e m. Existe um isomorfismo tal que: Bases
 Como definio arrhenius a los acidos
Como definio arrhenius a los acidos Dados os intervalos reais abaixo represente por extenso
Dados os intervalos reais abaixo represente por extenso Dado os intervalos reais abaixo represente os por extenso
Dado os intervalos reais abaixo represente os por extenso Série estatística conjugada
Série estatística conjugada Quantas possibilidades existem para a prole?
Quantas possibilidades existem para a prole? Lançam-se dois dados honestos com faces numeradas de 1 a 6
Lançam-se dois dados honestos com faces numeradas de 1 a 6 Isomorfismo transformação linear
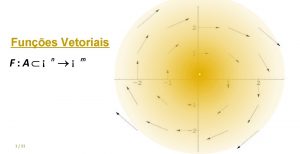
Isomorfismo transformação linear Modulo direção sentido
Modulo direção sentido Diferença entre grandeza escalar e vetorial
Diferença entre grandeza escalar e vetorial Espaço vetorial sobre um corpo
Espaço vetorial sobre um corpo Relido o poema de dois quartetos e dois tercetos
Relido o poema de dois quartetos e dois tercetos Isomorfismo organizzativo
Isomorfismo organizzativo Isomorfismo en minerales
Isomorfismo en minerales Isomorfismo gestalt
Isomorfismo gestalt Fenomeno perceptivo
Fenomeno perceptivo Tipos de problemas abn
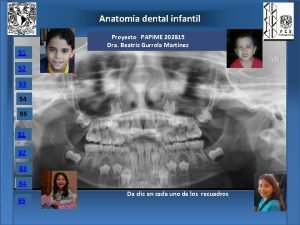
Tipos de problemas abn Anatomia dental infantil
Anatomia dental infantil Anatomia feminina fotos reais
Anatomia feminina fotos reais Determine as raízes reais das equações incompletas
Determine as raízes reais das equações incompletas Fluidos reais
Fluidos reais