Introduction to Graph theory Why do we care

Introduction to Graph “theory” • Why do we care about graph theory in testing and quality analysis? – The “flow” (both control and data) of a design, within a program or among programs may be depicted with a graphical representation. • Graph gives us the tool to formally study these graphical representations of flow and design test cases from the flow.

What is a graph ? • • A branch of topology—focus on connections (undirected) Graphs – – • nodes, edges, matrices degree of a node Paths Components Directed graphs – – – – nodes, edges indegree, outdegree paths and semi-paths n-connectedness cyclomatic number strong and weak components Program Graphs

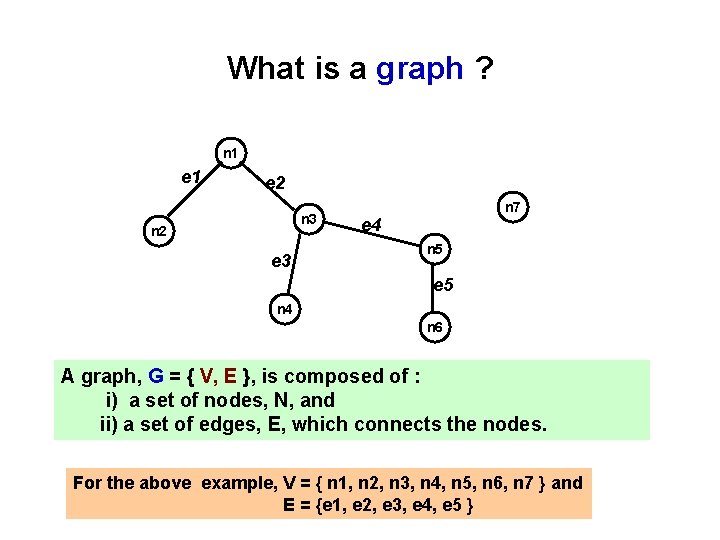
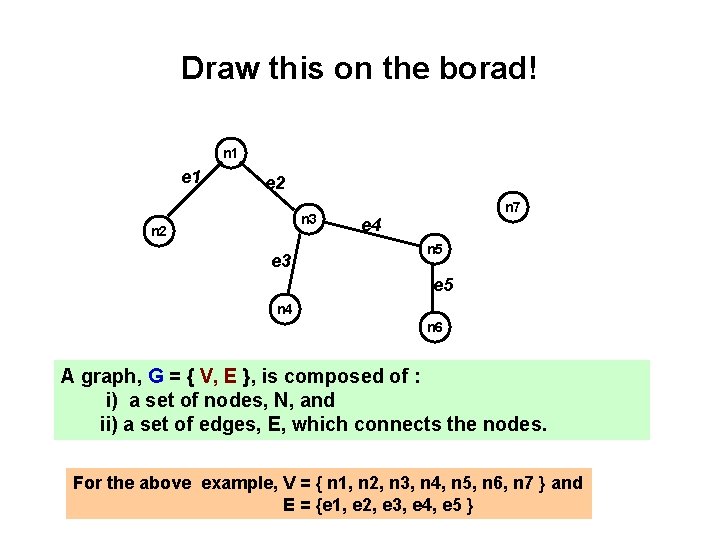
What is a graph ? n 1 e 2 n 3 n 2 e 3 n 7 e 4 n 5 e 5 n 4 n 6 A graph, G = { V, E }, is composed of : i) a set of nodes, N, and ii) a set of edges, E, which connects the nodes. For the above example, V = { n 1, n 2, n 3, n 4, n 5, n 6, n 7 } and E = {e 1, e 2, e 3, e 4, e 5 }

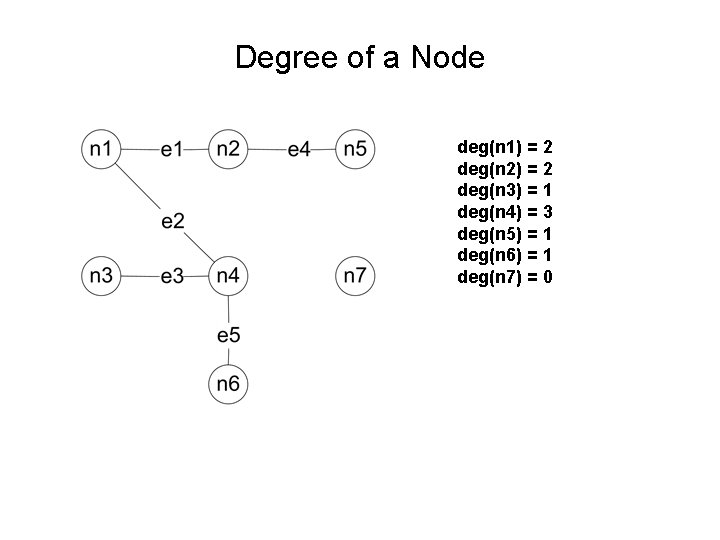
Degree of a node • Note that in the previous graph, not every node is immediately connected to another node; and some node is immediately connected to more than one other node. – For example: • N 7 is not connected to any other node • N 3 is connected to three other nodes: n 1, n 4 and n 5. • Formally, the “degree” of a node x, nx, is defined as the number of edges, e’s, that have node nx as the immediate end point. – This is the same as the number of other nodes that nx is immediately connected to • Degree (n 7) = 0 • Degree (n 3) = 3 For clarity, the definition uses edges, rather than immediately connect nodes.

Degree of a Node deg(n 1) = 2 deg(n 2) = 2 deg(n 3) = 1 deg(n 4) = 3 deg(n 5) = 1 deg(n 6) = 1 deg(n 7) = 0

Draw this on the borad! n 1 e 2 n 3 n 2 e 3 n 7 e 4 n 5 e 5 n 4 n 6 A graph, G = { V, E }, is composed of : i) a set of nodes, N, and ii) a set of edges, E, which connects the nodes. For the above example, V = { n 1, n 2, n 3, n 4, n 5, n 6, n 7 } and E = {e 1, e 2, e 3, e 4, e 5 }

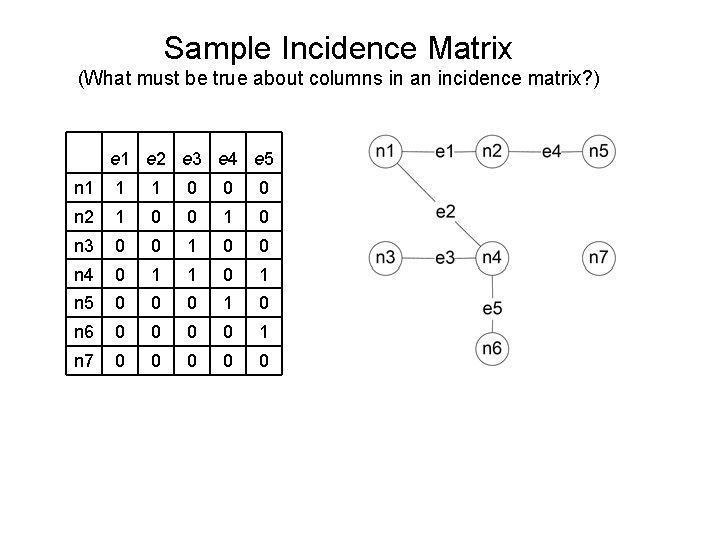
Using Incidence matrix to represent graph e 1 e 2 e 3 e 4 e 5 n 1 1 1 n 2 1 n 3 n 4 1 1 n 5 1 1 n 6 1 n 7 An incidence matrix of a graph composed of J nodes and K edges is a J x K cross-product relation, where the rows are the nodes and the columns are the edges. The relation, in this case, is “immediately connected. ” For this example, the incidence matrix represents a 7 x 5 cross-product relation. The 1 in a cell, (x, y) represents that node, nx, is the end point of edge, ey. The empty cells may be filled with 0’s. 1)The sum of 1’s for any row, which represents a node, is the degree of that node. - e. g. sum of 1’s for node , n 5, is 2; therefore degree(n 5) = 2 2)Each column shows the edge, ex, and the 1’s in that column shows the nodes that edge, ex, connects (note each column always adds up to 2. )

Sample Incidence Matrix (What must be true about columns in an incidence matrix? ) e 1 e 2 e 3 e 4 e 5 n 1 1 1 0 0 0 n 2 1 0 0 1 0 n 3 0 0 1 0 0 n 4 0 1 1 0 1 n 5 0 0 0 1 0 n 6 0 0 1 n 7 0 0 0

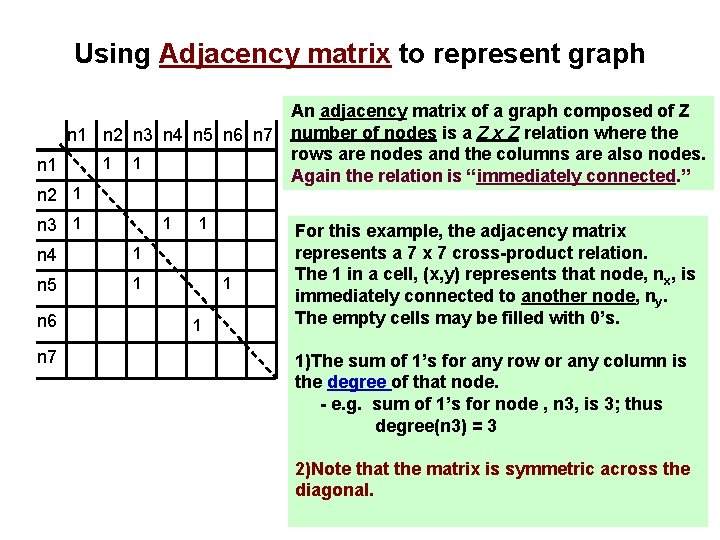
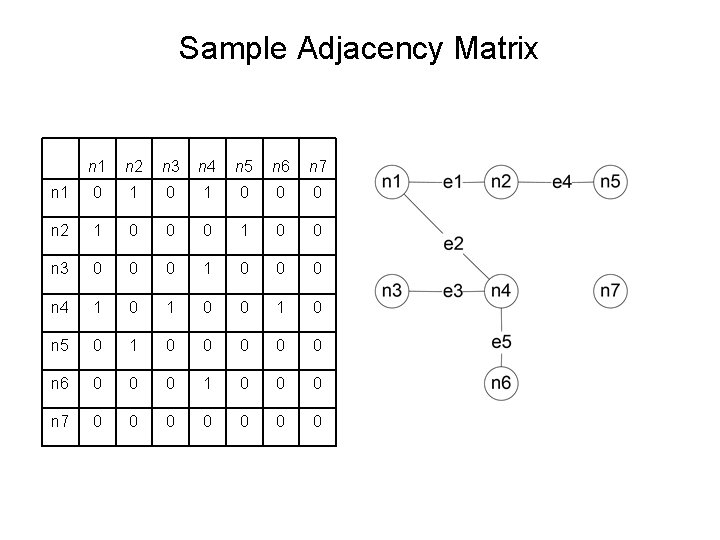
Using Adjacency matrix to represent graph An adjacency matrix of a graph composed of Z n 1 n 2 n 3 n 4 n 5 n 6 n 7 number of nodes is a Z x Z relation where the rows are nodes and the columns are also nodes. 1 1 n 1 Again the relation is “immediately connected. ” n 2 1 n 3 1 1 n 4 1 n 5 1 n 6 n 7 1 1 1 For this example, the adjacency matrix represents a 7 x 7 cross-product relation. The 1 in a cell, (x, y) represents that node, nx, is immediately connected to another node, ny. The empty cells may be filled with 0’s. 1)The sum of 1’s for any row or any column is the degree of that node. - e. g. sum of 1’s for node , n 3, is 3; thus degree(n 3) = 3 2)Note that the matrix is symmetric across the diagonal.

Sample Adjacency Matrix n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 1 0 1 0 0 0 n 2 1 0 0 0 1 0 0 n 3 0 0 0 1 0 0 0 n 4 1 0 0 1 0 n 5 0 1 0 0 0 n 6 0 0 0 1 0 0 0 n 7 0 0 0 0

Path • Note that we used the term, “immediately connected” for degree of a node. • A path in a graph is a sequence of immediately connected nodes: e. g. {nj, -- - , nj+z } in the graph where nj is immediately connected to nj+1, and node nj+1 is immediately connected to nj+2, and so on to node nj+z. • A path in a graph may also be defined as a sequence of edges, such that for any pair of edges, ei and ej, in the sequence, the edges share a common node.

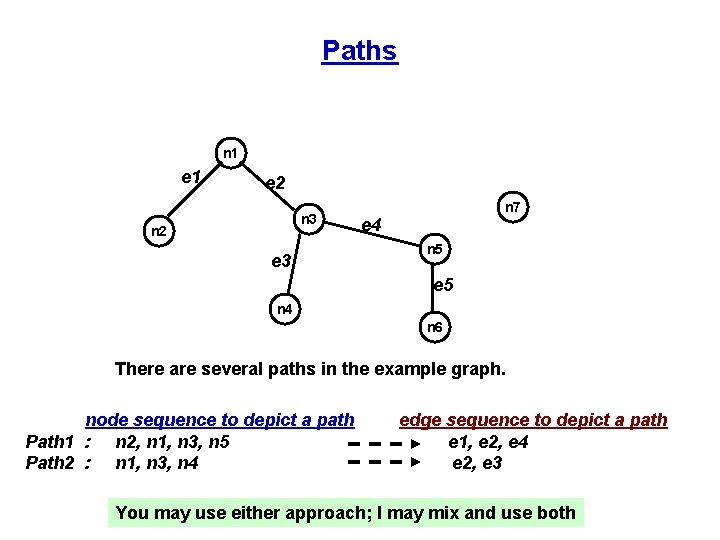
Paths n 1 e 2 n 3 n 2 e 3 n 7 e 4 n 5 e 5 n 4 n 6 There are several paths in the example graph. node sequence to depict a path Path 1 : n 2, n 1, n 3, n 5 Path 2 : n 1, n 3, n 4 edge sequence to depict a path e 1, e 2, e 4 e 2, e 3 You may use either approach; I may mix and use both

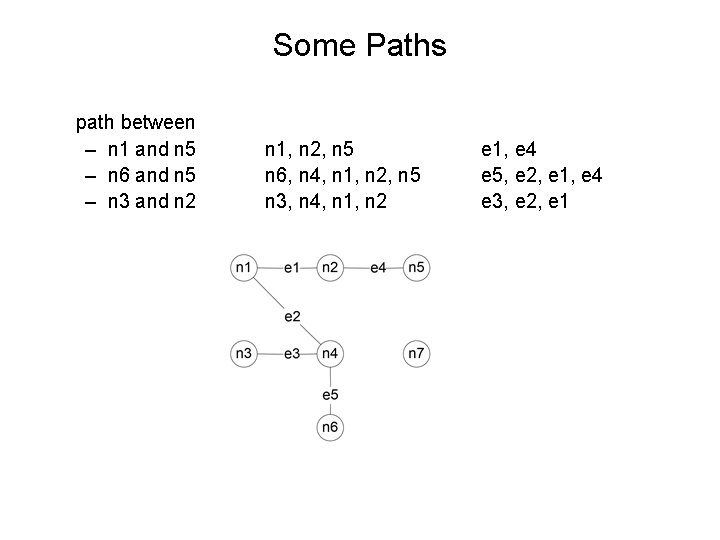
Some Paths path between – n 1 and n 5 – n 6 and n 5 – n 3 and n 2 n 1, n 2, n 5 n 6, n 4, n 1, n 2, n 5 n 3, n 4, n 1, n 2 e 1, e 4 e 5, e 2, e 1, e 4 e 3, e 2, e 1

Connected nodes (Connectedness) • Earlier two nodes are said to be immediately connected if there is an edge that connect the two nodes. The degree of a node was determined by the number of its immediately connected nodes. • Now a more general notion of connectedness of two nodes may be given. Node nx is connected to node ny if there is a path from nx to ny

Properties of Connectedness • Connected nodes on a path have some interesting relational properties: – It is reflexive because every node is connected to itself and thus is on the same path. – It is symmetric because nodes ni and nj on a path implies that nodes nj and ni are also on the same path. – It is transitive for nodes ni and nj on a path and nodes nj and nk on the same path implies that ni and nk are on the same path also. Note: This relation of ‘connected’ satisfies the definition of equivalence relation.

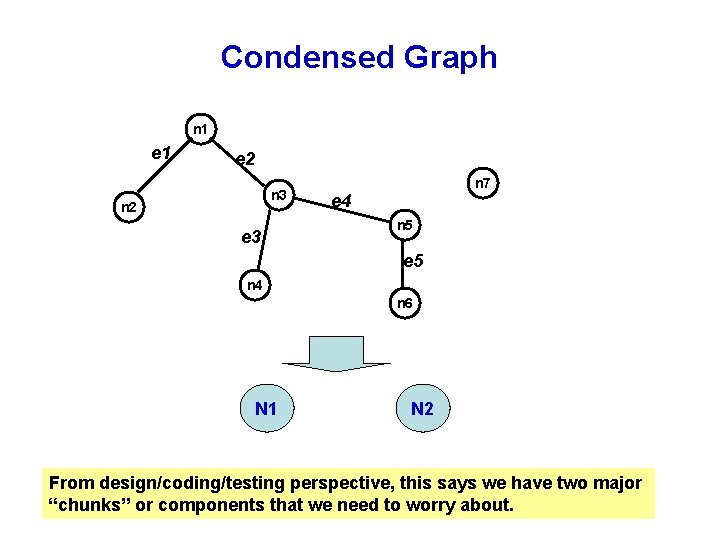
Component and condensation graph • A component of a graph is defined as the maximal set of connected nodes. – From our graph example: • {n 1, n 2, n 3, n 4, n 5, n 6} form a component • {n 7} also forms a component • A condensation graph is formed by replacing each component in the original graph by a “condensed” single node. There are no edges. – Condensation graph of a graph gives us a view of the “complexity” through the number of components.

Condensed Graph n 1 e 2 n 3 n 2 e 3 n 7 e 4 n 5 e 5 n 4 n 6 N 1 N 2 From design/coding/testing perspective, this says we have two major “chunks” or components that we need to worry about.

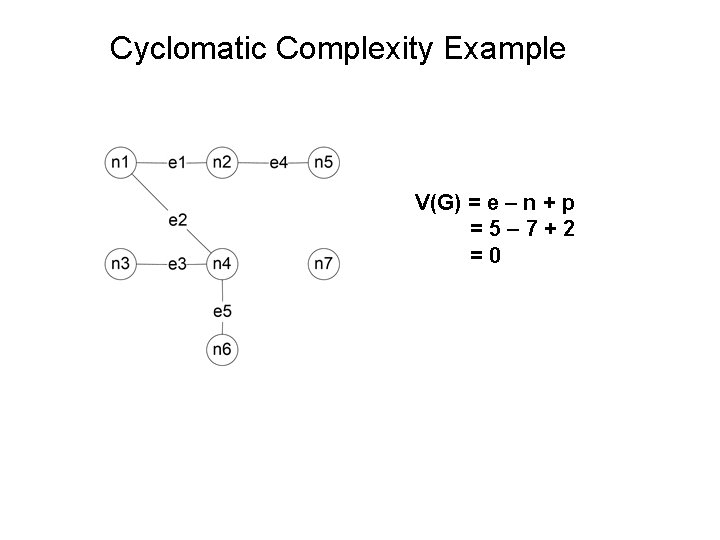
Cyclomatic Number of a Graph The cyclomatic number of a graph G is given by V(G) = e – n + p, where – e is the number of edges in G – n is the number of nodes in G – p is the number of components in G • Cyclomatic complexity pertains to both ordinary and directed graphs (next topic). • The graph must be strongly connected. • not very useful on our running example because it is not strongly connected. We will see this part in the future chapters.

Cyclomatic Complexity Example V(G) = e – n + p =5– 7+2 =0

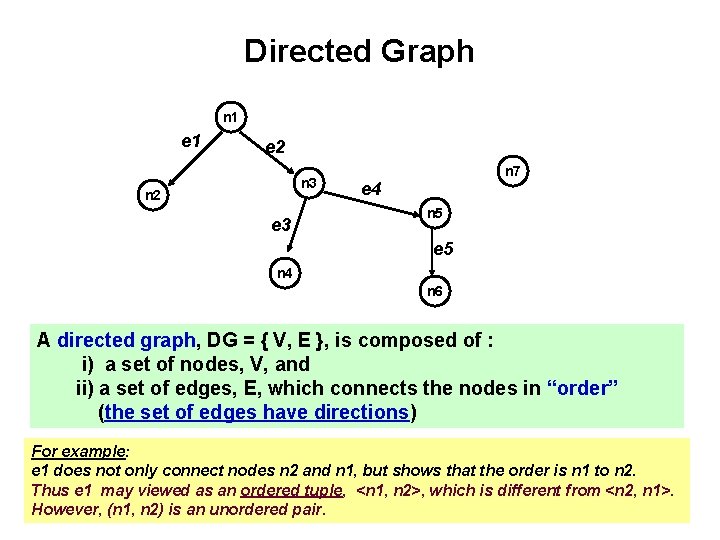
Directed Graph n 1 e 2 n 3 n 2 e 3 n 7 e 4 n 5 e 5 n 4 n 6 A directed graph, DG = { V, E }, is composed of : i) a set of nodes, V, and ii) a set of edges, E, which connects the nodes in “order” (the set of edges have directions) For example: e 1 does not only connect nodes n 2 and n 1, but shows that the order is n 1 to n 2. Thus e 1 may viewed as an ordered tuple, <n 1, n 2>, which is different from <n 2, n 1>. However, (n 1, n 2) is an unordered pair.

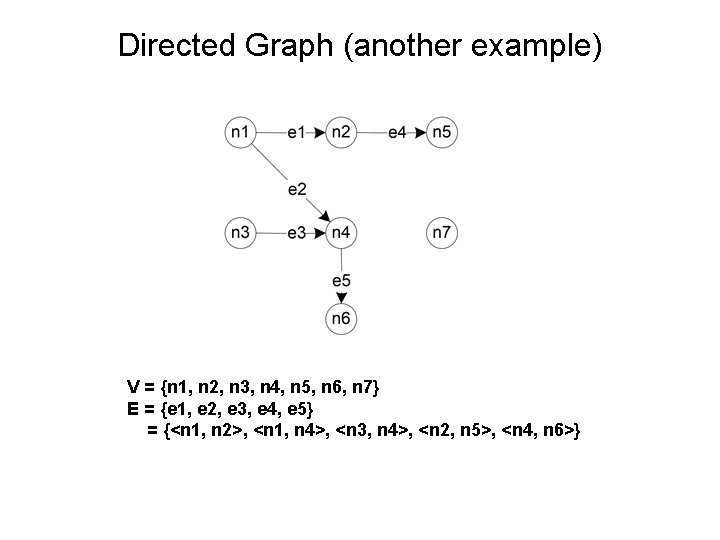
Directed Graph (another example) V = {n 1, n 2, n 3, n 4, n 5, n 6, n 7} E = {e 1, e 2, e 3, e 4, e 5} = {<n 1, n 2>, <n 1, n 4>, <n 3, n 4>, <n 2, n 5>, <n 4, n 6>}

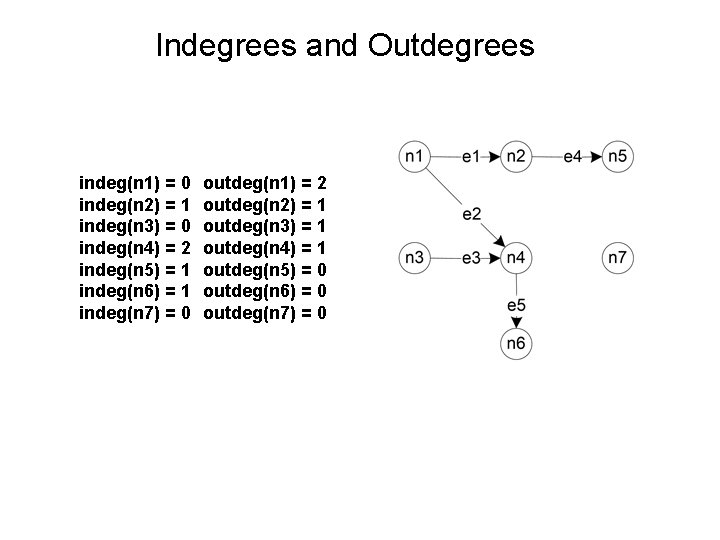
Degrees of Directed Graph • With directed graph, one can utilize the directional concept. – – • e. g. the flow of a program, the control flow in imperative programming language, can be represented by directed graph. Each edge not only connects nodes but shows a direction (like a vector). For each node, n, in the graph, there may be defined: 1. Indegree (n) = the number of distinct edges immediately directed in and towards n. 2. Outdegree (n) = number of distinct edges immediately directed out and away from n. Note that for any node, n: degree (n) = indegree (n) + outdegree (n)

Indegrees and Outdegrees indeg(n 1) = 0 indeg(n 2) = 1 indeg(n 3) = 0 indeg(n 4) = 2 indeg(n 5) = 1 indeg(n 6) = 1 indeg(n 7) = 0 outdeg(n 1) = 2 outdeg(n 2) = 1 outdeg(n 3) = 1 outdeg(n 4) = 1 outdeg(n 5) = 0 outdeg(n 6) = 0 outdeg(n 7) = 0

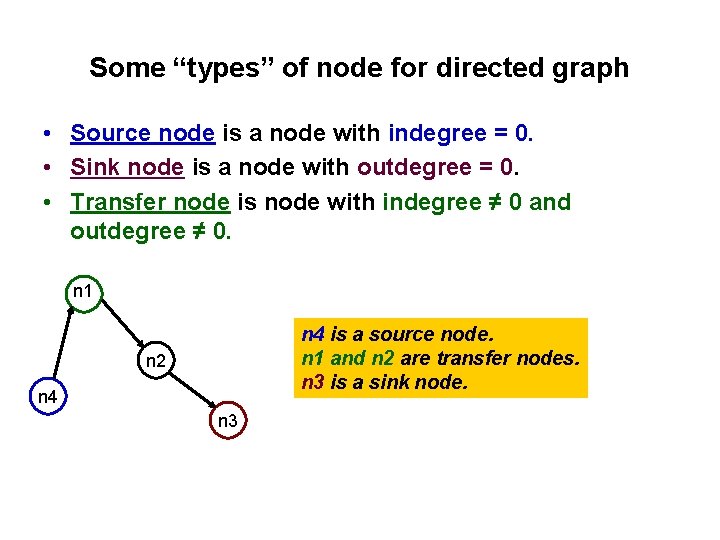
Some “types” of node for directed graph • Source node is a node with indegree = 0. • Sink node is a node with outdegree = 0. • Transfer node is node with indegree ≠ 0 and outdegree ≠ 0. n 1 n 4 is a source node. n 1 and n 2 are transfer nodes. n 3 is a sink node. n 2 n 4 n 3

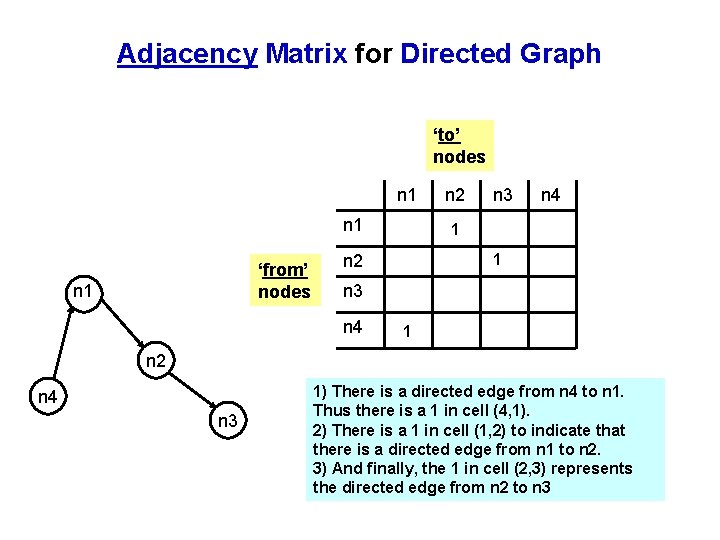
Adjacency Matrix for Directed Graph ‘to’ nodes n 1 ‘from’ nodes n 1 n 2 n 3 n 4 1 n 2 n 4 n 3 1) There is a directed edge from n 4 to n 1. Thus there is a 1 in cell (4, 1). 2) There is a 1 in cell (1, 2) to indicate that there is a directed edge from n 1 to n 2. 3) And finally, the 1 in cell (2, 3) represents the directed edge from n 2 to n 3

Path and semi-path • With directed graph, the notion of a path is not just connection, but there is a directional connection. – 1. A directed path is a sequence of edges such that for any adjacent pair of edges, e 1 and e 2, the terminal node for e 1 is the starting node for e 2. – 2. A cycle is a directed path that begins and ends at the same node – 3. A chain is a sequence of nodes in which every interior node has indegree = outdegree = 1 – 4. A directed semi-path is a sequence of edges such that, for at least one adjacent pair of edges, ei and ej, in the sequence, the initial node of the first edge is the same initial node of the second edge or the terminating node of the first edge is the same as the terminating node of the second edge.

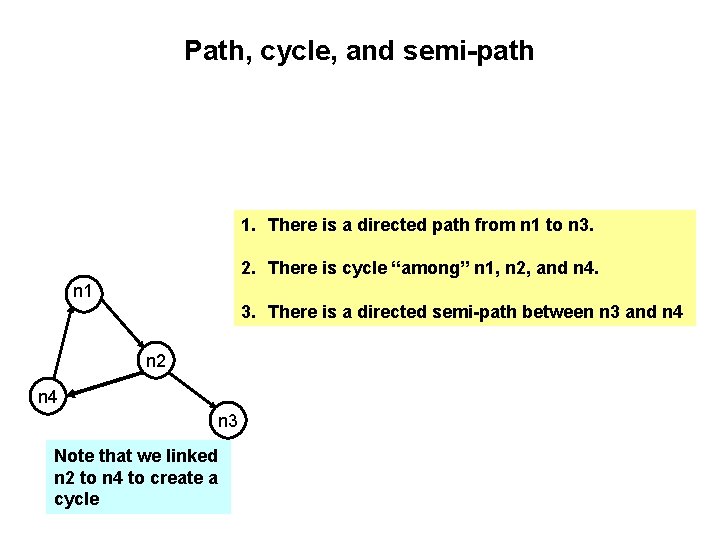
Path, cycle, and semi-path 1. There is a directed path from n 1 to n 3. 2. There is cycle “among” n 1, n 2, and n 4. n 1 3. There is a directed semi-path between n 3 and n 4 n 2 n 4 n 3 Note that we linked n 2 to n 4 to create a cycle

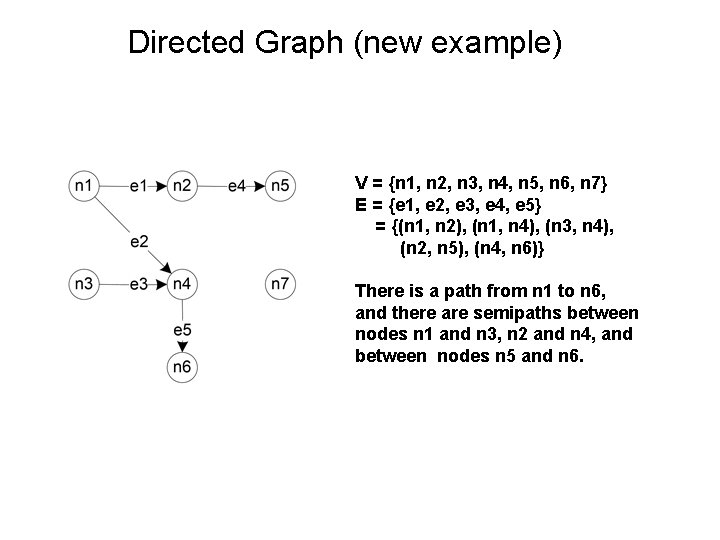
Directed Graph (new example) V = {n 1, n 2, n 3, n 4, n 5, n 6, n 7} E = {e 1, e 2, e 3, e 4, e 5} = {(n 1, n 2), (n 1, n 4), (n 3, n 4), (n 2, n 5), (n 4, n 6)} There is a path from n 1 to n 6, and there are semipaths between nodes n 1 and n 3, n 2 and n 4, and between nodes n 5 and n 6.

Reachability with Adjacent Matrix Operations • Adjacent matrix for a directed graph indicates the directional connection of the nodes, not a two way connection. Note that an edge that connects nodes, nx and ny does not mean it connects ny and nx in the reverse way. So for directed graph the “connect” operation is non-symmetric. • We can use matrix operation on Adjacent matrix of the directed graph to view the paths in the directed graph.

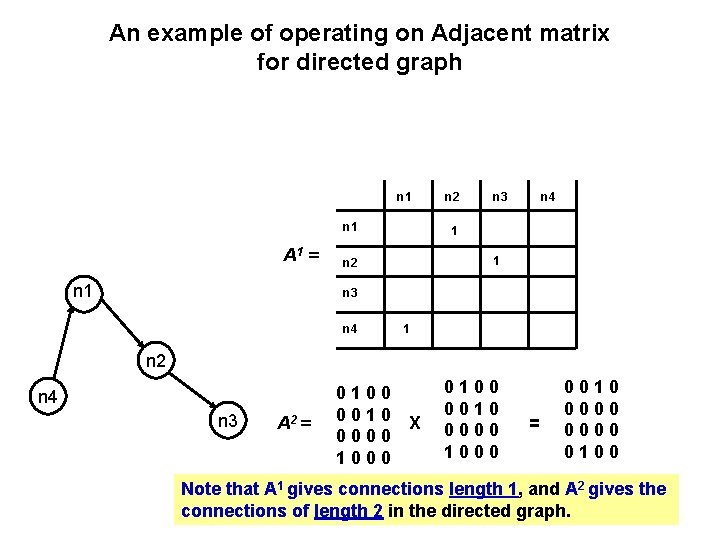
An example of operating on Adjacent matrix for directed graph n 1 A 1 = n 1 n 2 n 3 n 4 1 n 2 n 4 n 3 A 2 = 0100 0010 0000 1000 X 0100 0010 0000 1000 = 0010 0000 0100 Note that A 1 gives connections length 1, and A 2 gives the connections of length 2 in the directed graph.

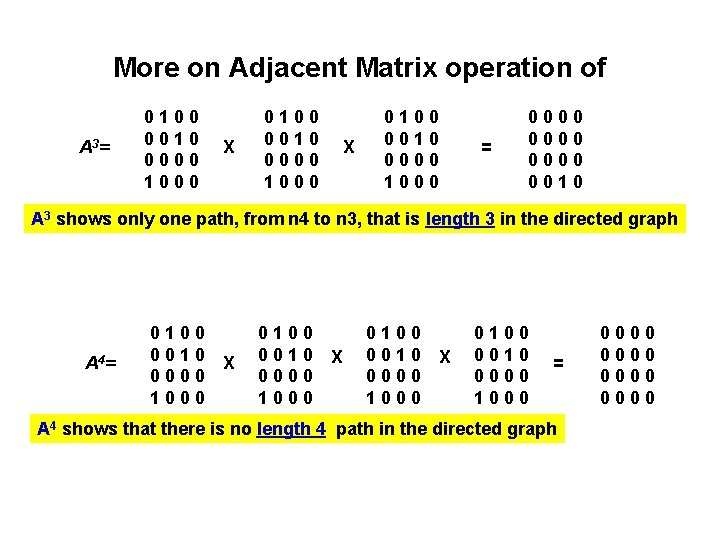
More on Adjacent Matrix operation of A 3 = 0100 0010 0000 1000 X 0100 0010 0000 1000 = 0000 0010 A 3 shows only one path, from n 4 to n 3, that is length 3 in the directed graph A 4 = 0100 0010 0000 1000 X 0100 0010 0000 1000 = A 4 shows that there is no length 4 path in the directed graph 0000

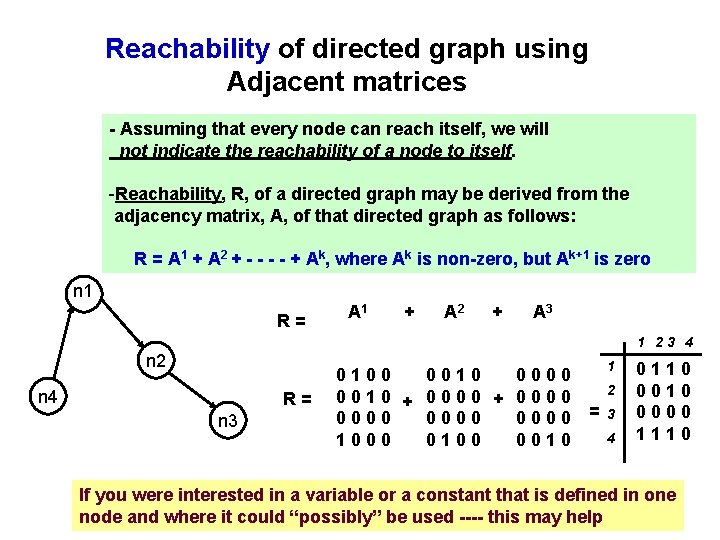
Reachability of directed graph using Adjacent matrices - Assuming that every node can reach itself, we will not indicate the reachability of a node to itself. -Reachability, R, of a directed graph may be derived from the adjacency matrix, A, of that directed graph as follows: R = A 1 + A 2 + - - + Ak, where Ak is non-zero, but Ak+1 is zero n 1 R= A 1 + A 2 + A 3 1 23 4 n 2 n 4 R= n 3 0100 0010 0000 0010 + 0000 0000 1000 0100 0010 1 2 = 3 4 0110 0000 1110 If you were interested in a variable or a constant that is defined in one node and where it could “possibly” be used ---- this may help

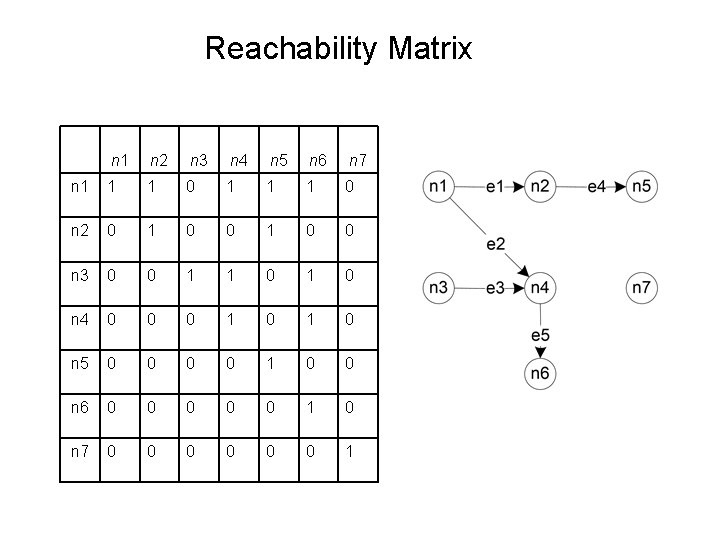
Reachability Matrix n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 1 1 1 0 n 2 0 1 0 0 n 3 0 0 1 1 0 n 4 0 0 0 1 0 n 5 0 0 1 0 0 n 6 0 0 0 1 0 n 7 0 0 0 1

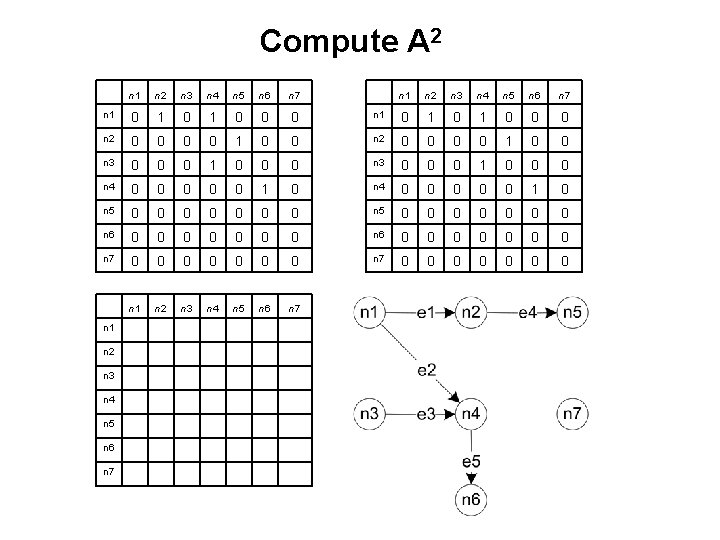
Compute A 2 n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 1 0 1 0 0 0 n 2 0 0 1 0 n 3 0 0 0 1 0 n 4 0 0 n 5 0 0 0 n 6 0 0 n 7 0 n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 1 0 1 0 0 n 2 0 0 1 0 0 n 3 0 0 0 1 0 n 4 0 0 0 1 0 0 0 n 5 0 0 0 n 6 0 0 0 0 n 7 0 0 0 0 n 2 n 3 n 4 n 5 n 6 n 7

n-Connectedness Nodes nj and nk in a directed graph are – 0 -connected iff no path (or semipath) exists between nj and nk – 1 -connected iff a semi-path but no path exists between nj and nk – 2 -connected iff a path exists from nj and nk – 3 -connected iff a path goes from nj to nk and a path goes from nk to nj • No other degrees of n-connectedness exist • A new edge, e 6, is added to our continuing example. • n-connectedness has very useful expressive power.

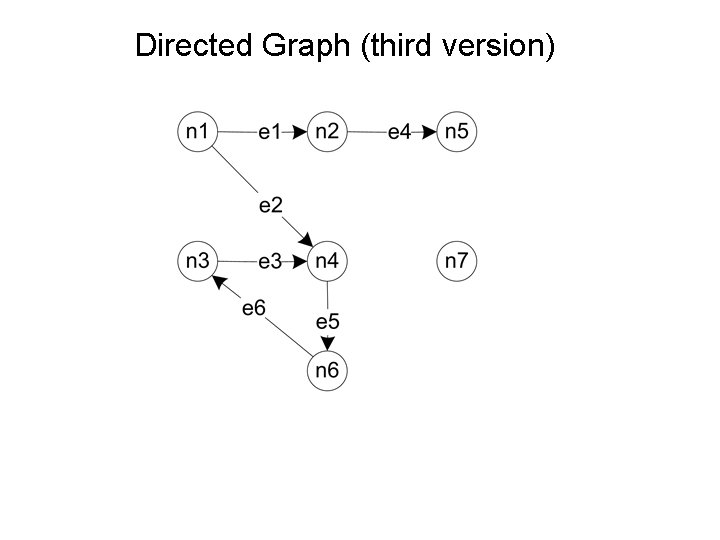
Directed Graph (third version)

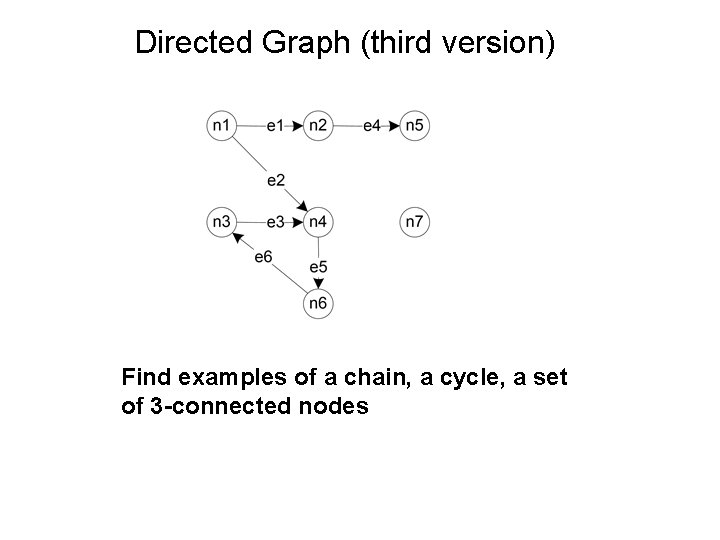
Directed Graph (third version) Find examples of a chain, a cycle, a set of 3 -connected nodes

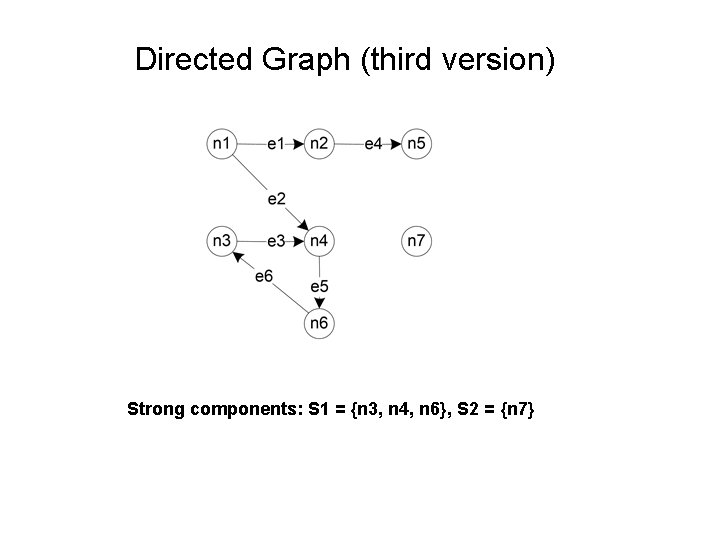
Strong Components of a Directed Graph A strong component of a directed graph is a maximal set of 3 -connected nodes. Strong components. . . – identify loops and isolated nodes. – lead to another form of condensation graph – support an excellent view of testing programs with loops

Directed Graph (third version) Strong components: S 1 = {n 3, n 4, n 6}, S 2 = {n 7}

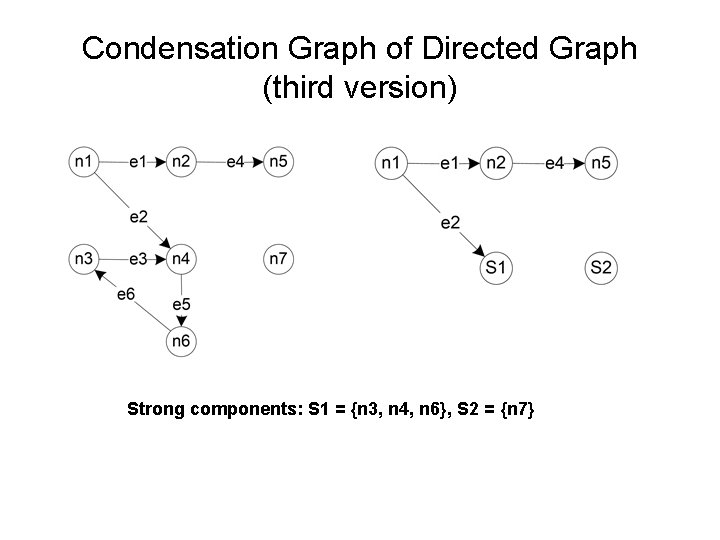
Condensation Graph of a Directed Graph Given a directed graph D = (V, E), its condensation graph is formed by replacing strongly connected nodes by their corresponding strong components. A condensation graph of a directed graph. . . – contains no loops, and is therefore – a Directed Acyclic Graph (DAG) – support an excellent view of testing programs with loops

Condensation Graph of Directed Graph (third version) Strong components: S 1 = {n 3, n 4, n 6}, S 2 = {n 7}

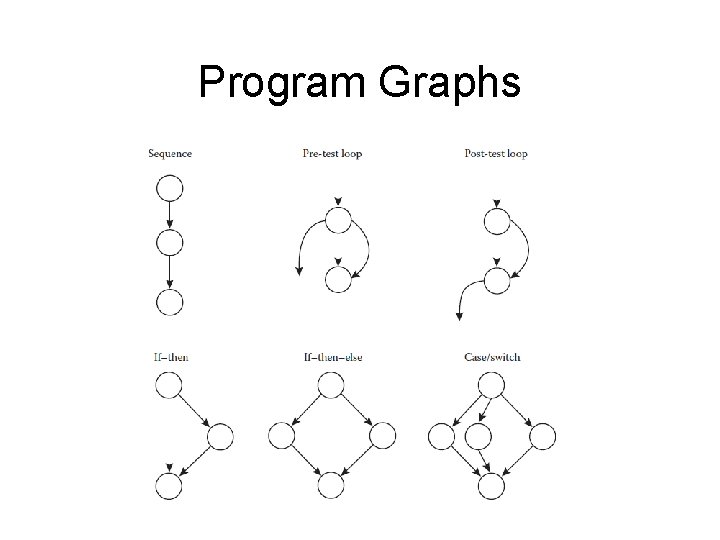
Program Graphs The program graph of a program written in an imperative programming language is a directed graph in which nodes are either entire statements or statement fragments. There is an edge from node i to node j if and only if node j can be executed immediately after node i). • (The early (1970 s) definitions referred to nodes as entire statements, but this doesn’t fit well with modern programming languages. ) • We shall use “statement fragment” to refer either to full statements or to statement fragments.

Program Graphs

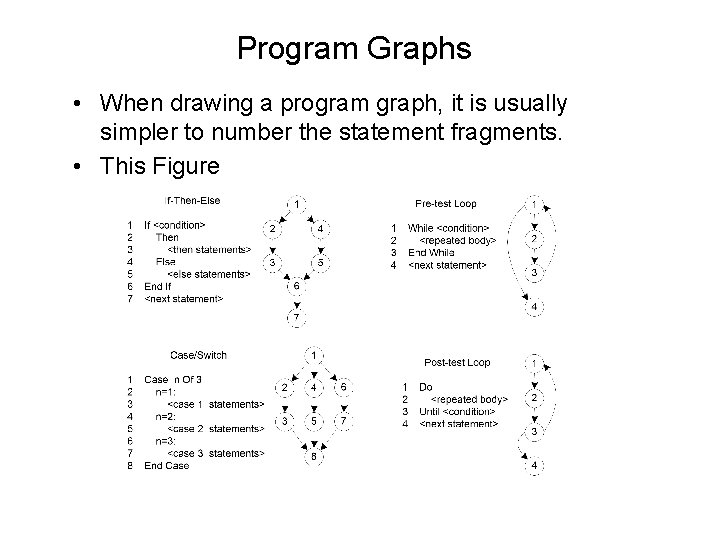
Program Graphs • When drawing a program graph, it is usually simpler to number the statement fragments. • This Figure

Four Graph-Based Models • • Finite State Machines Petri Nets Event-Driven Petri Nets State. Charts • These are all executable models, i. e. , it is possible to build a program (an engine) to execute the model.

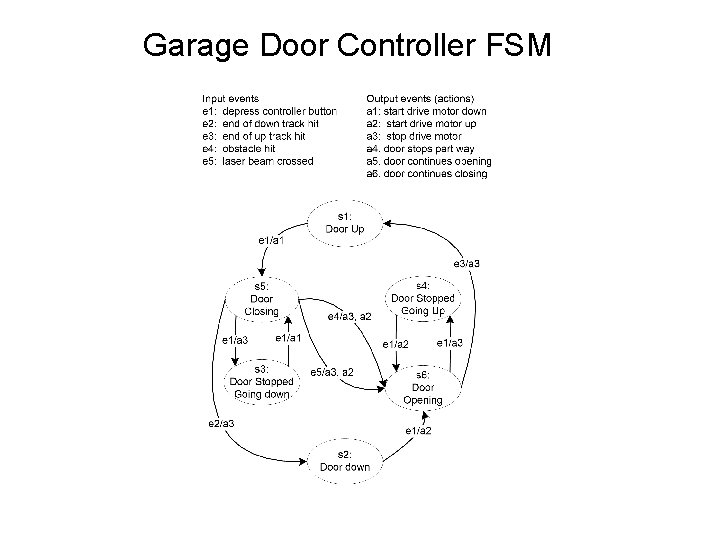
Finite State Machines (FSMs) • Finite State Machines are directed graphs in which nodes are states, and edges are transitions from one state to a successor state. • Transitions are caused by – events – date conditions – passage of time (an event) • Constraints – states are mutually exclusive – only one transition can occur at a time • FSMs are ideally suited for menu-driven applications

Garage Door Controller FSM

Graph Representations Will need these later: • Program Control Flows: sequential, if-then-else, loop, etc. • State Transition Diagram (Finite State Machines): states and stimuli Will not use: • Petri Net: a complex set of events and transitions • State Charts: A complicated (embedding of states) form of State Transition Diagram