http www eng fsu edumpf EEL 4930 6

http: //www. eng. fsu. edu/~mpf EEL 4930 § 6 / 5930 § 5, Spring ‘ 06 Physical Limits of Computing Slides for a course taught by Michael P. Frank in the Department of Electrical & Computer Engineering M. Frank, "Physical Limits of Computing"

Physical Limits of Computing Course Outline Currently I am working on writing up a set of course notes based on this outline, intended to someday evolve into a textbook I. Course Introduction Moore’s Law vs. Modern Physics II. Foundations Required Background Material in Computing & Physics III. Fundamentals The Deep Relationships between Physics and Computation 1/25/2022 IV. Core Principles The two Revolutionary Paradigms of Physical Computation V. Technologies Present and Future Physical Mechanisms for the Practical Realization of Information Processing VI. Conclusion M. Frank, "Physical Limits of Computing" 2

Part II. Foundations • This first part of the course quickly reviews some key background knowledge that you will need to be familiar with in order to follow the later material. – You may have seen some of this material before. • Part II is divided into two “chapters: ” – Chapter II. A. Theory of Information and Computation – Chapter II. B. Required Physics Background 1/25/2022 M. Frank, "Physical Limits of Computing" 3

Chapter II. B. Required Physics Background • This chapter covers “All the Physics You Need to Know, ” for purposes of this course… – §II. B. 1. Physical Quantities, Units, and Constants – §II. B. 2. Modern Formulations of Mechanics – §II. B. 3. Basics of Relativity Theory – §II. B. 4. Elementary Quantum Mechanics – §II. B. 5. Thermodynamics & Statistical Mechanics – §II. B. 6. Solid-State Physics 1/25/2022 M. Frank, "Physical Limits of Computing" 4

Section II. B. 1: Physical Quantities, Units, and Fundamental Constants Unit prefixes, Physical quantities, Dimensional identities, Planck units, Physical constants M. Frank, "Physical Limits of Computing"

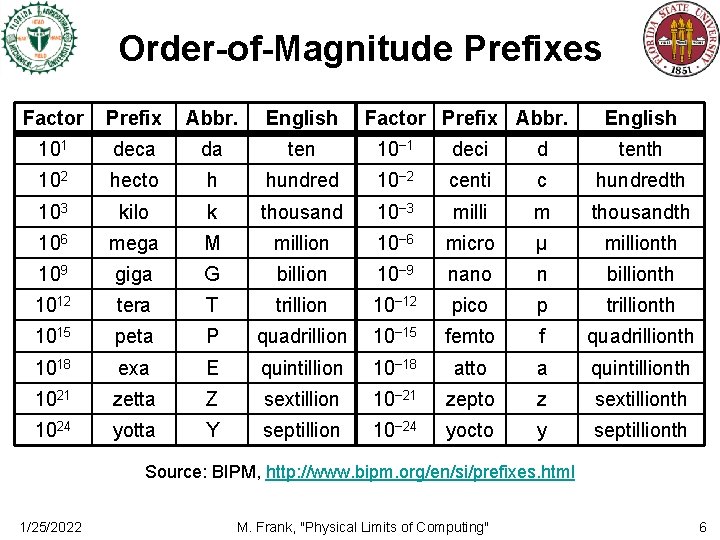
Order-of-Magnitude Prefixes Factor Prefix Abbr. English 101 deca da ten 10− 1 deci d tenth 102 hecto h hundred 10− 2 centi c hundredth 103 kilo k thousand 10− 3 milli m thousandth 106 mega M million 10− 6 micro μ millionth 109 giga G billion 10− 9 nano n billionth 1012 tera T trillion 10− 12 pico p trillionth 1015 peta P quadrillion 10− 15 femto f quadrillionth 1018 exa E quintillion 10− 18 atto a quintillionth 1021 zetta Z sextillion 10− 21 zepto z sextillionth 1024 yotta Y septillion 10− 24 yocto y septillionth Source: BIPM, http: //www. bipm. org/en/si/prefixes. html 1/25/2022 M. Frank, "Physical Limits of Computing" 6

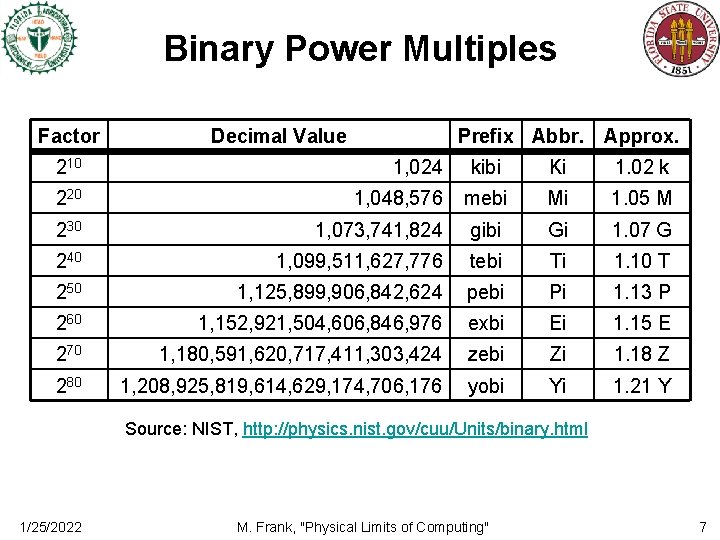
Binary Power Multiples Factor Decimal Value Prefix Abbr. 210 1, 024 220 1, 048, 576 230 Approx. kibi Ki 1. 02 k mebi Mi 1. 05 M 1, 073, 741, 824 gibi Gi 1. 07 G 240 1, 099, 511, 627, 776 tebi Ti 1. 10 T 250 1, 125, 899, 906, 842, 624 pebi Pi 1. 13 P 260 1, 152, 921, 504, 606, 846, 976 exbi Ei 1. 15 E 270 1, 180, 591, 620, 717, 411, 303, 424 zebi Zi 1. 18 Z 280 1, 208, 925, 819, 614, 629, 174, 706, 176 yobi Yi 1. 21 Y Source: NIST, http: //physics. nist. gov/cuu/Units/binary. html 1/25/2022 M. Frank, "Physical Limits of Computing" 7

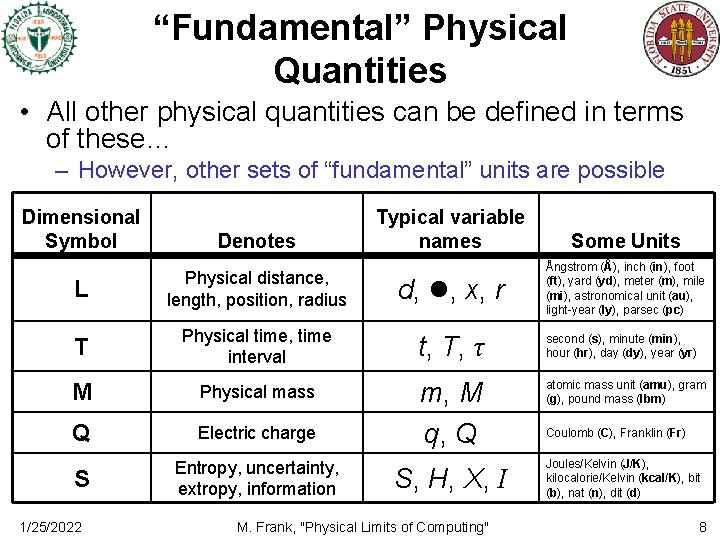
“Fundamental” Physical Quantities • All other physical quantities can be defined in terms of these… – However, other sets of “fundamental” units are possible Dimensional Symbol Denotes Typical variable names Some Units Ångstrom (Å), inch (in), foot (ft), yard (yd), meter (m), mile (mi), astronomical unit (au), light-year (ly), parsec (pc) L Physical distance, length, position, radius d, , x, r T Physical time, time interval t, T, τ second (s), minute (min), hour (hr), day (dy), year (yr) M Physical mass atomic mass unit (amu), gram (g), pound mass (lbm) Q Electric charge m, M q, Q S Entropy, uncertainty, extropy, information S, H, X, I Joules/Kelvin (J/K), kilocalorie/Kelvin (kcal/K), bit (b), nat (n), dit (d) 1/25/2022 M. Frank, "Physical Limits of Computing" Coulomb (C), Franklin (Fr) 8

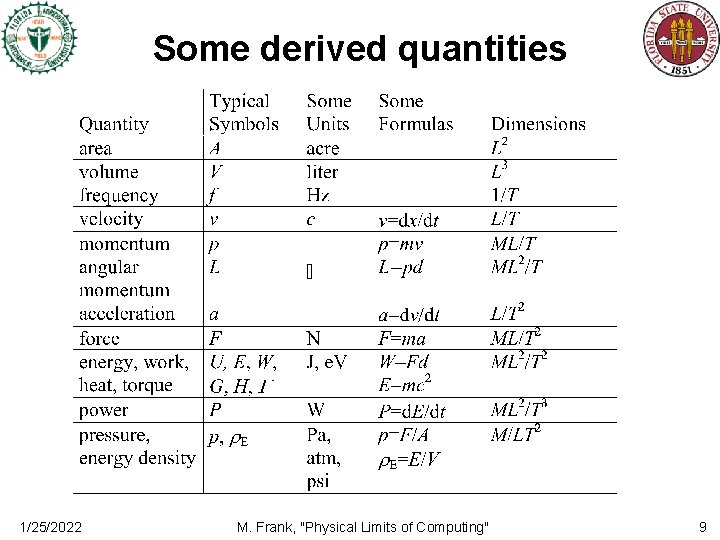
Some derived quantities 1/25/2022 M. Frank, "Physical Limits of Computing" 9

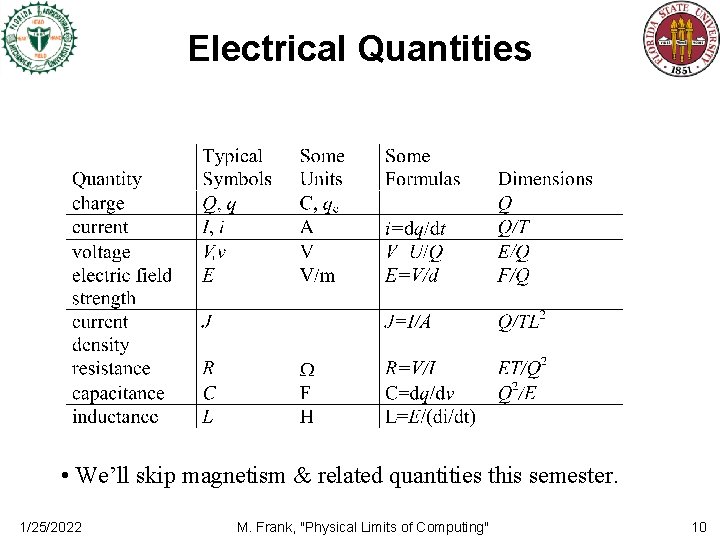
Electrical Quantities • We’ll skip magnetism & related quantities this semester. 1/25/2022 M. Frank, "Physical Limits of Computing" 10

Fundamental Physical Constants • The speed of light in vacuum: c = 299, 792, 458 m/s – This value is exact, by the very definition of the meter! • The energy of frequency (Planck’s constant): h = 6. 6260755× 10 34 J s – The energy of angular frequency (reduced Planck’s constant) = h / 2 • Remember this with the analogy: (h : 1 circle) : : ( : 1 radian) – In fact, later we’ll see why it’s valid to view h, as being these angles. • The force of gravity (Newton’s gravitational constant): G = 6. 67259× 10 11 N m 2 / kg • The force of electricity (Coulomb’s law constant): k. C = 8. 9876 109 N m 2 / C 2 • The e-fold of uncertainty (Boltzmann’s constant): k = k. B = Log[e] = 1. 3806513× 10 23 J / K • Others: permittivity of free space, Stefan-Boltzmann constant, etc. to be introduced later, as we go along. 1/25/2022 M. Frank, "Physical Limits of Computing" 11

Constants and Laws • Each of the fundamental constants arises as a simple proportionality constant in some fundamental physical law: – Newton’s Law. Bodies exert an attractive force proportional to their masses and the inverse square of their separation: Fgrav = G·(m 1 m 2/d 2) – Coulomb’s Law. Electrical charges exert a force proportional to their charges and the inverse square of their separation: Felec = k. C·(q 1 q 2/d 2) – Constancy of the speed of light (Maxwell). The distance traversed by an electromagnetic disturbance (e. g. , light) is proportional to the elapsed time: = c·t – Boltzmann’s Relation. The amount of energy added to a system as heat is proportional to its temperature times the increase in its information capacity. d. E = k. B·{T d(Log[W])} – Quantization principle (Planck, Einstein). Electromagnetic disturbances come in discrete units (quanta) having an energy proportional to their frequency: E = h·f 1/25/2022 M. Frank, "Physical Limits of Computing" 12

The Unification of Physical Quantities • By letting fundamental constants be dimensionless, we can establish identities between different physical dimensions: – If we let G be dimensionless, we get: • M=L 3/T 2 (mass = rate of acceleration of volume? ) – If we let k. C be dimensionless, we get: • Q 2=ML 3/T 2 (charge squared = mass volume acceleration? ) – This is how charge units such as the Franklin/statcoulomb/electrostatic unit are defined • With both G and k. C dimensionless, we get Q=M (charge=mass) – If we let c be dimensionless, we get: • T=L (time=length), and E=M (energy=mass). • With G dimensionless also, we get M=L. – If we let k. B be dimensionless, we get: • T=E/S (temperature = energy per unit uncertainty) – If we let h be dimensionless, we get: • E=1/T (energy=inverse time, or frequency) • p=1/L (momentum=inverse length, or spatial frequency) • If c is also dimensionless, we get M=1/L. • and if G is also dimensionless, we get 1/L=M=L L=1 (dimensionless!) 1/25/2022 M. Frank, "Physical Limits of Computing" 13

Planck’s Natural Units • Max Planck realized in 1898 that letting G, c, h be dimensionless implied that all of the basic quantities L, T, M were “really” dimensionless quantities also… – I. e. , any length, time, or mass quantity corresponds to a unique pure number determined by G, c and h! • Thus, length/time/mass have associated “natural” units for measuring them • The units discovered by Planck are: – The Planck length LP = (G /c 3)1/2 ≈ 1. 6 10− 35 m – The Planck time t. P = (G /c 5)1/2 ≈ 5. 4 10− 44 s – The Planck mass m. P = ( c/G)1/2 ≈ 22 μg • It’s thought that these units (or something close to them) will be seen to have fundamental significance – in the presumed eventual unified “theory of everything” 1/25/2022 M. Frank, "Physical Limits of Computing" 14

Physics that you should already know • We’ll assume you already know these well, and won’t review them: – Basic Newtonian mechanics • Newton’s laws, motion, energy, etc. – Basic electrostatics • Ohm’s law, Kirchoff’s laws, etc. • Also helpful, but not prerequisite (we’ll introduce them as we go along): – Basic statistical mechanics & thermodynamics – Basic quantum mechanics – Basic relativity theory 1/25/2022 M. Frank, "Physical Limits of Computing" 15

Section II. B. 2: Modern Formulations of Mechanics Euler-Lagrange Equation, Least. Action Principle, Hamilton’s Equations, Field Theories M. Frank, "Physical Limits of Computing"

Chapter II. B. Required Physics Background • This chapter covers “All the Physics You Need to Know, ” for purposes of this course… – §II. B. 1. Physical Quantities, Units, and Constants – §II. B. 2. Modern Formulations of Mechanics – §II. B. 3. Basics of Relativity Theory – §II. B. 4. Quantum Mechanics – §II. B. 5. Thermodynamics & Statistical Mechanics – §II. B. 6. Solid-State Physics 1/25/2022 M. Frank, "Physical Limits of Computing" 17

Generalized Mechanics • Classical mechanics (Newton’s Laws, etc. ) can be expressed in the most general and concise way using the Lagrangian and Hamiltonian formulations. – Developed by Lagrange and Hamilton in the 1800’s. • Each of these is based on a simple energy-valued function of the system’s instantaneous state: – The Lagrangian: Kinetic minus potential energy. – The Hamiltonian: Kinetic plus potential energy. • The dynamical laws for the system can be derived from either of these energy functions, – due to general principles of dynamics. • The Lagrangian (or Hamiltonian) gives the laws of physics! • This framework generalizes to be the basis for quantum mechanics, quantum field theories, etc. 1/25/2022 M. Frank, "Physical Limits of Computing" 18

Euler-Lagrange Equation Note the time-derivative over-dot! or just Where: • L(q, v) is the system’s Lagrangian function. • qi : ≡ Generalized position coordinate with index i. • vi : ≡ Generalized velocity coordinate i; • or (as appropriate) • t : ≡ Time coordinate – In a given frame of reference. 1/25/2022 M. Frank, "Physical Limits of Computing" 19

Euler-Lagrange example • Let q = (qi) (with i {1, 2, 3}) be the ordinary x, y, z coordinates of a point particle with mass m. • Let L = ½mvi 2 − V(q). (Kinetic minus pot. energy) • Then, ∂L/∂qi = −∂V/∂qi = Fi – The force component in direction i. • Meanwhile, ∂L/∂vi = ∂(½mvi 2)/∂vi = mvi = pi – The momentum component in direction i. • And, – Mass times acceleration in direction i. • So we get Fi = mai or 1/25/2022 (Newton’s 2 nd law) M. Frank, "Physical Limits of Computing" 20

Least-Action Principle A. k. a. Hamilton’s principle • The action of an energy quantity means the integral of that quantity over time. – Dimensions of action: ET = ML 2/T ~ 1 • The trajectory specified by the Euler-Lagrange equation locally extremizes (usually minimizes) the action of the Lagrangian: – Among trajectories s(t) between specified points s(t 0) and s(t 1). • Infinitesimal deviations from this trajectory leave the action unchanged, to 1 st order. – “Physical systems always take the path of least action” 1/25/2022 M. Frank, "Physical Limits of Computing" 21

Hamilton’s Equations • The Hamiltonian is defined as H : ≡ vipi − L. – Equals Ek + Ep if L = Ek − Ep and vipi = 2 Ek = mvi 2. Implicit summation over i here. • We can then describe the dynamics of (q, p) states using the 1 st-order Hamilton’s equations: • These are equivalent to the 2 nd-order Euler. Lagrange equation. – But sometimes are easier to solve than it. • Note that any Hamiltonian dynamics is what we might call bi-deterministic – Meaning, deterministic in both the forwards and reverse time directions. 1/25/2022 M. Frank, "Physical Limits of Computing" 22

Lagrangian Formulation of Field Theories • Here, the space of indices i of the generalized coordinates is continuous (thus uncountable). – Usually it forms some topological space T, e. g. , ℝ 3. – So, we often use φ(x) notation in place of qi. • In local field theories, the Lagrangian L(φ) is the integral of a Lagrange density function ℒ(x) – where the point x ranges over the entire space T. • This ℒ(x) depends only locally on the field φ, e. g. , ℒ(x) = ℒ [φ(x), (∂φ/∂xi)(x), (x)] • All successful physical theories (so far) can be explicitly written down as local field theories! – Thus, there is no instantaneous action at a distance. 1/25/2022 M. Frank, "Physical Limits of Computing" 23

Section II. B. 3: Basics of Relativity Theory Special Relativity, The Speed-of -Light Limit, General Relativity, Black Holes M. Frank, "Physical Limits of Computing"

Chapter II. B. Required Physics Background • This chapter covers “All the Physics You Need to Know, ” for purposes of this course… – §II. B. 1. Physical Quantities, Units, and Constants – §II. B. 2. Modern Formulations of Mechanics – §II. B. 3. Basics of Relativity Theory – §II. B. 4. Quantum Mechanics – §II. B. 5. Thermodynamics & Statistical Mechanics – §II. B. 6. Solid-State Physics 1/25/2022 M. Frank, "Physical Limits of Computing" 25

Subsection II. B. 3. a: Special Relativity and the Speed-of-Light Limit, Relativistic Effects, Lorentz Transformation, Relativistic Energy/Momentum M. Frank, "Physical Limits of Computing"

The Speed-of-Light Limit • No form of information (including quantum information!) can propagate through space at a velocity (relative to its local surroundings) that is greater than the speed of light, c ≈ 3× 108 m/s. • Some consequences of the limit: – No closed system can propagate faster than c. • Although you can define open systems that do, by definition – No given piece of matter, energy, or momentum can propagate faster than c. • All conserved physical quantities flow through space in a local fashion. – The influence of all of the fundamental physical forces (including gravity) propagates at (at most) c. – The probability mass associated with a quantum particle (or configuration of a multiparticle system) flows through space (or configuration space) in an entirely local fashion, at no faster than c. 1/25/2022 M. Frank, "Physical Limits of Computing" 27

Early History of the Limit • The principle of locality was first anticipated by Newton – He expressed a desire to get rid of the “action at a distance” aspects of his law of gravitation. • The fact of the finiteness of the speed of light (So. L) was first observed experimentally by Roemer in 1676. – The first decent speed estimate was obtained by Fizeau in 1849. • Weber & Kohlrausch derived a constant velocity value, c, from empirical electromagnetic constants (ε 0, μ 0) in 1856. – Kirchoff pointed out the match with the empirical speed of light in 1857. • Maxwell showed that his EM theory implied the existence of waves that always propagate at c in 1873. – Hertz later confirmed experimentally that EM waves indeed existed • Michaelson & Morley (1887) observed that the empirical So. L was independent of the observer’s (Earth’s) state of motion! – Maxwell’s equations are apparently valid in all inertial reference frames! – Fitzgerald (1889), Lorentz (1892, 1899), Larmor (1898), Poincaré (1898, 1904), & Einstein (1905) explored the implications of this. . . 1/25/2022 M. Frank, "Physical Limits of Computing" 28

Relativity: Non-intuitive, but True • How can the speed of something be a fundamental constant? Seems broken at first… – If I’m moving at some large velocity v towards you, and I shoot a laser pulse at you, at what speed does the pulse travel, relative to me, and to you? • The answer to both is exactly c! (Not v+c or anything else!) • Newton’s laws were the same in all frames of reference moving at a constant velocity. – Einstein’s Principle of Relativity (Po. R): All laws of physics are invariant under changes in velocity • Einstein’s insight: The Po. R is perfectly logically consistent w. Maxwell’s theory of a constant So. L! – But, in showing consistency, we must change our definition of the concepts of space and time! 1/25/2022 M. Frank, "Physical Limits of Computing" 29

Some Consequences of Relativity • Measured lengths and time intervals in a system vary depending on the system’s velocity – relative to the observers making the measurements • In particular, relativity yields the following effects: – The length of any moving object is shortened… • in its direction of motion. – All physical processes in a moving object run more slowly, • Faster motion through space Slower motion “through time!” – The mass of any moving object is amplified. • Energy and mass are really the same quantity, measured in different units! A realization that led to – The conversion between units is given by E=mc 2. • Nothing (including energy, matter, information, etc. ) can travel faster than light! (So. L limit. ) 1/25/2022 M. Frank, "Physical Limits of Computing" 30

Three Ways to “Understand” the c limit • Energy of motion contributes to mass of object. – Mass approaches as velocity c. – Infinite energy would be needed to reach c. • Due to the form of the equations, lengths and times in a faster-than-light moving object would become imaginary numbers! – What would that even mean, physically? • Faster than light in one reference frame Backwards in time in another reference frame – Sending information backwards in time violates causality, leads to logical contradictions! 1/25/2022 M. Frank, "Physical Limits of Computing" 31

The c limit in quantum physics • Sometimes you see statements about “non-local” effects in quantum systems. Watch out! – Even Einstein made this mistake. • He described a quantum thought experiment that at first appeared to require “spooky action at a distance. ” – Later, it was shown that such experiments did not actually violate the speed-of-light limit for information. • All of the apparently “non-local” quantum effects can be explained away as mere illusions… – emergent phenomena that are predicted by an entirely local underlying theory fully respecting the So. L limit. . • Widely-separated systems can still maintain quantum correlations (entanglement), – but that isn’t “true” non-locality, in the usual sense. 1/25/2022 M. Frank, "Physical Limits of Computing" 32

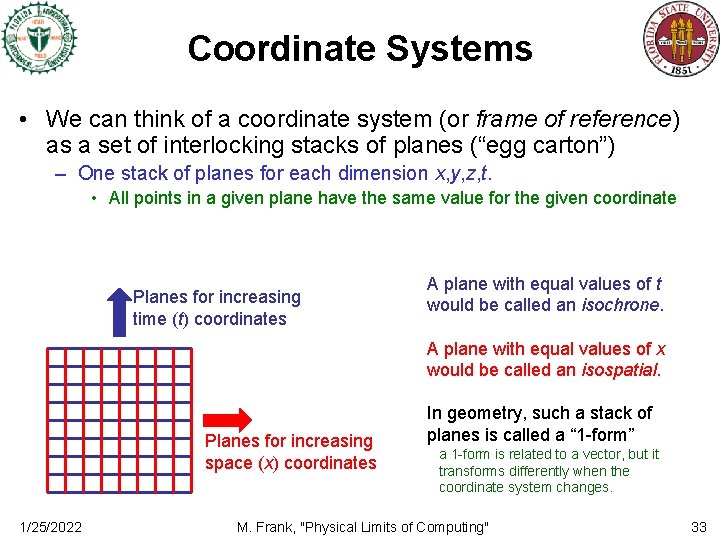
Coordinate Systems • We can think of a coordinate system (or frame of reference) as a set of interlocking stacks of planes (“egg carton”) – One stack of planes for each dimension x, y, z, t. • All points in a given plane have the same value for the given coordinate Planes for increasing time (t) coordinates A plane with equal values of t would be called an isochrone. A plane with equal values of x would be called an isospatial. Planes for increasing space (x) coordinates 1/25/2022 In geometry, such a stack of planes is called a “ 1 -form” a 1 -form is related to a vector, but it transforms differently when the coordinate system changes. M. Frank, "Physical Limits of Computing" 33

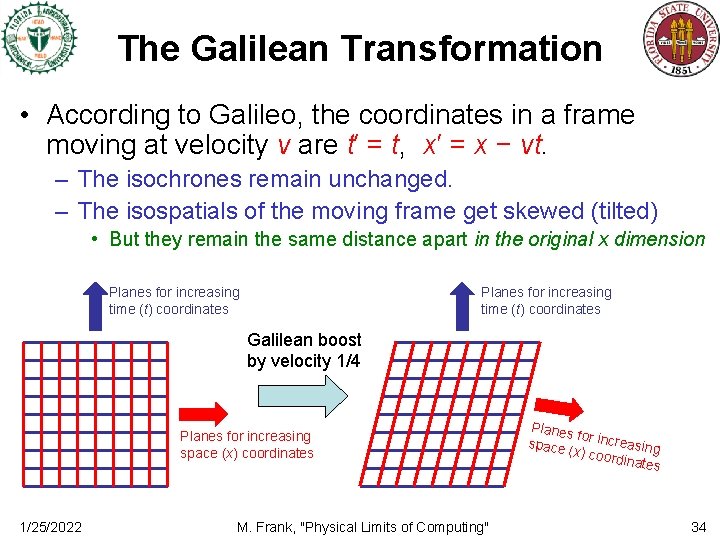
The Galilean Transformation • According to Galileo, the coordinates in a frame moving at velocity v are t′ = t, x′ = x − vt. – The isochrones remain unchanged. – The isospatials of the moving frame get skewed (tilted) • But they remain the same distance apart in the original x dimension Planes for increasing time (t) coordinates Galilean boost by velocity 1/4 Planes for increasing space (x) coordinates 1/25/2022 M. Frank, "Physical Limits of Computing" Planes for incr e space (x) coo asing rdinate s 34

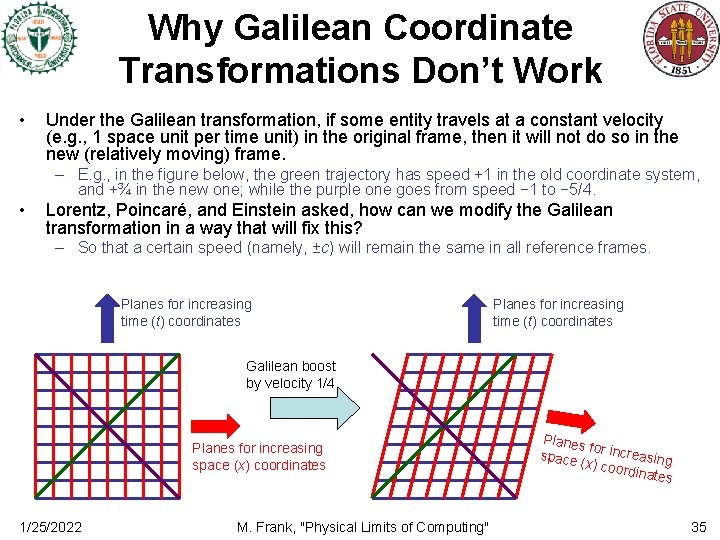
Why Galilean Coordinate Transformations Don’t Work • Under the Galilean transformation, if some entity travels at a constant velocity (e. g. , 1 space unit per time unit) in the original frame, then it will not do so in the new (relatively moving) frame. – E. g. , in the figure below, the green trajectory has speed +1 in the old coordinate system, and +¾ in the new one; while the purple one goes from speed − 1 to − 5/4. • Lorentz, Poincaré, and Einstein asked, how can we modify the Galilean transformation in a way that will fix this? – So that a certain speed (namely, ±c) will remain the same in all reference frames. Planes for increasing time (t) coordinates Galilean boost by velocity 1/4 Planes for increasing space (x) coordinates 1/25/2022 M. Frank, "Physical Limits of Computing" Planes for incr e space (x) coo asing rdinate s 35

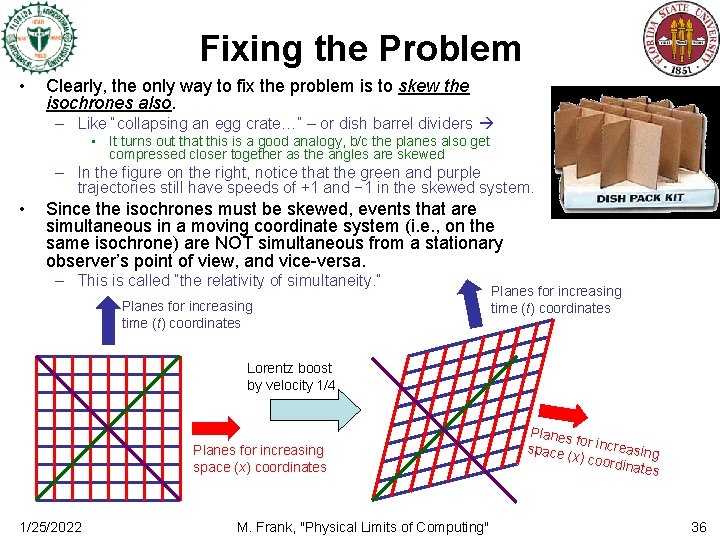
Fixing the Problem • Clearly, the only way to fix the problem is to skew the isochrones also. – Like “collapsing an egg crate…” – or dish barrel dividers • It turns out that this is a good analogy, b/c the planes also get compressed closer together as the angles are skewed – In the figure on the right, notice that the green and purple trajectories still have speeds of +1 and − 1 in the skewed system. • Since the isochrones must be skewed, events that are simultaneous in a moving coordinate system (i. e. , on the same isochrone) are NOT simultaneous from a stationary observer’s point of view, and vice-versa. – This is called “the relativity of simultaneity. ” Planes for increasing time (t) coordinates Lorentz boost by velocity 1/4 Planes for increasing space (x) coordinates 1/25/2022 M. Frank, "Physical Limits of Computing" Planes for incr e space (x) coo asing rdinate s 36

The Lorentz Transformation Usually credited to Lorentz (1904), but actually it was written down earlier; e. g. , Larmor (1897), and a variant form by Voigt (1887) • Lorentz, Poincaré: Maxwell’s laws remain unchanged in the reference frame (x′, t′) of an object moving with constant velocity v = Δx/Δt in another reference frame (x, t), if we postulate the following transformation between the coordinate systems: where Note: Our γ symbol in these slides denotes the reciprocal of the quantity that’s called γ by most authors. We do this so that we can write β 2 + 2 = 1. 1/25/2022 M. Frank, "Physical Limits of Computing" 37

Some Consequences of the Lorentz Transform • Length contraction: (Fitzgerald 1889, Lorentz 1892) – An object having length in its rest frame appears, when measured in a relatively moving frame, to have the (shorter) length γ. • For lengths that are parallel to the direction of motion. • Time dilation: (Larmor 1897, Poincaré 1898) – If time interval τ is measured between two co-located events in a given frame, a (larger) time t = τ/γ will be measured between those same two events in a relatively moving frame. • Mass expansion: (Einstein’s fix for Newton’s F=ma) – If an object has mass m 0>0 in its rest frame, then it is seen to have the (larger) mass m = m 0/γ in a relatively moving frame. 1/25/2022 M. Frank, "Physical Limits of Computing" 38

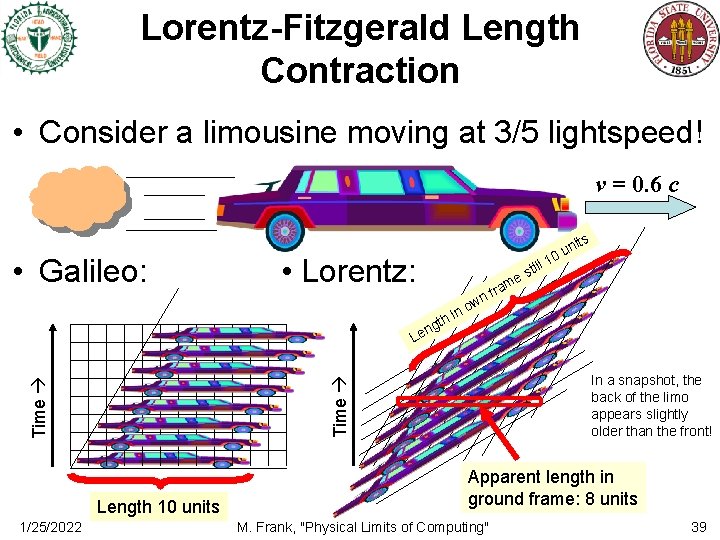
Lorentz-Fitzgerald Length Contraction • Consider a limousine moving at 3/5 lightspeed! v = 0. 6 c its • Galileo: • Lorentz: th ng in f wn till es 1 n 0 u ram o Le Time Length 10 units 1/25/2022 In a snapshot, the back of the limo appears slightly older than the front! Apparent length in ground frame: 8 units M. Frank, "Physical Limits of Computing" 39

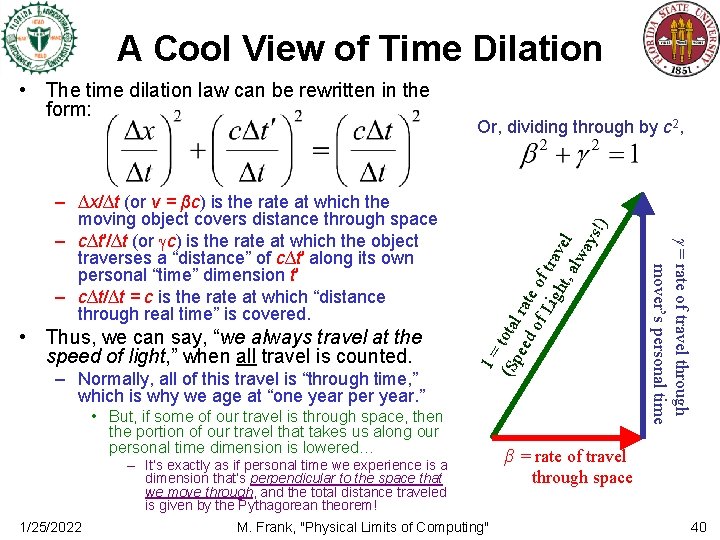
A Cool View of Time Dilation • Thus, we can say, “we always travel at the speed of light, ” when all travel is counted. – Normally, all of this travel is “through time, ” which is why we age at “one year per year. ” !) • But, if some of our travel is through space, then the portion of our travel that takes us along our personal time dimension is lowered… – It’s exactly as if personal time we experience is a dimension that’s perpendicular to the space that we move through, and the total distance traveled is given by the Pythagorean theorem! 1/25/2022 M. Frank, "Physical Limits of Computing" = rate of travel through mover’s personal time – ∆x/∆t (or v = βc) is the rate at which the moving object covers distance through space – c∆t′/∆t (or c) is the rate at which the object traverses a “distance” of c∆t′ along its own personal “time” dimension t′ – c∆t/∆t = c is the rate at which “distance through real time” is covered. Or, dividing through by c 2, 1= (Sp total eed rat of e of Lig tra ht, vel alw ays • The time dilation law can be rewritten in the form: β = rate of travel through space 40

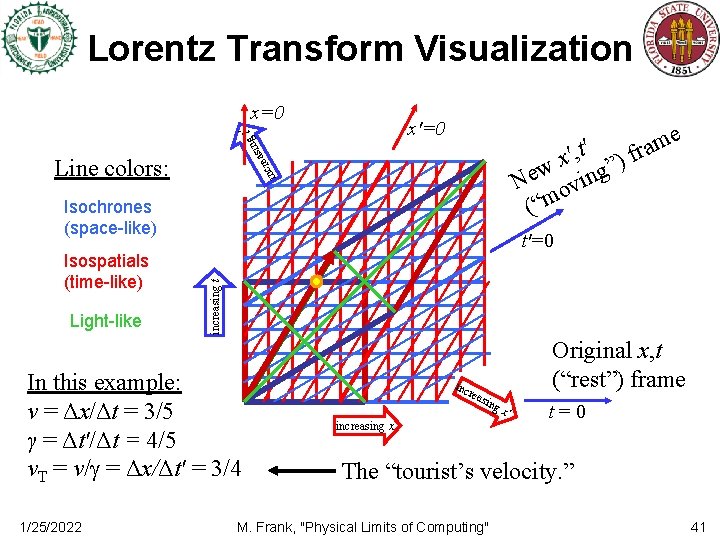
Lorentz Transform Visualization x=0 ng asi t′ x′=0 inc re Line colors: e m ′ a ′, t ) fr x w ing” e N ov (“m Isochrones (space-like) Light-like increasing t Isospatials (time-like) t′=0 In this example: v = Δx/Δt = 3/5 γ = Δt′/Δt = 4/5 v. T = v/ = Δx/Δt′ = 3/4 1/25/2022 inc rea Original x, t (“rest”) frame sin increasing x gx ′ t=0 The “tourist’s velocity. ” M. Frank, "Physical Limits of Computing" 41

• In this animation, – We see the instantaneous coordinate system of an observer moving along a non-uniform trajectory. • Small dots are events – E. g. , supernova explosions • Large dots are events that the traveler experiences in equal amounts of his own time. Increasing t′ coordinates Lorentz Transform Animation Future light cone Past light cone Increasing x′ coordinates – E. g. , birthday parties he has, each time he’s aged a year • Note that dots on fast-moving parts of the trajectory seem farther apart – until he matches velocities – This is due to the time dilation effect 1/25/2022 M. Frank, "Physical Limits of Computing" 42

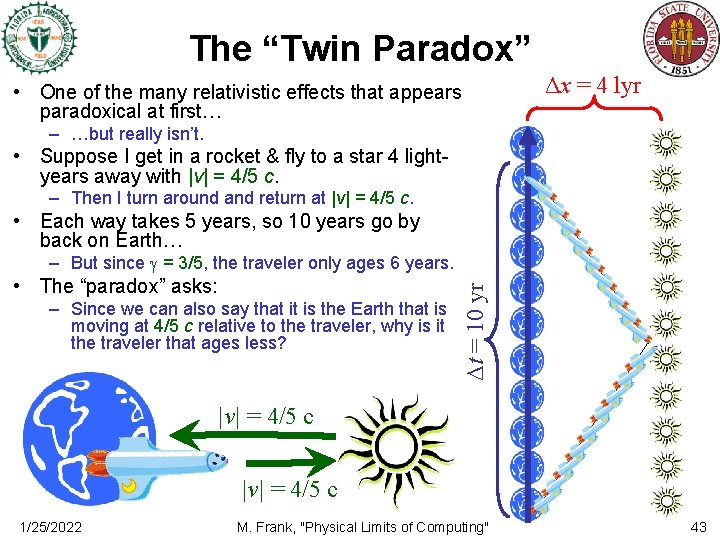
The “Twin Paradox” • One of the many relativistic effects that appears paradoxical at first… Δx = 4 lyr – …but really isn’t. • Suppose I get in a rocket & fly to a star 4 lightyears away with |v| = 4/5 c. – Then I turn around and return at |v| = 4/5 c. • Each way takes 5 years, so 10 years go by back on Earth… • The “paradox” asks: – Since we can also say that it is the Earth that is moving at 4/5 c relative to the traveler, why is it the traveler that ages less? Δt = 10 yr – But since = 3/5, the traveler only ages 6 years. |v| = 4/5 c 1/25/2022 M. Frank, "Physical Limits of Computing" 43

Resolution of the Paradox • The reason for the asymmetry is that – the traveler is the one who has changed between coordinate systems! • when he turned around! • Remember the skewed isochrones in the moving frame? – During our 3 -year outbound trip, • we consider only 3 = 9/5 = 1. 8 years to go by back on Earth. – Yes, Earth is also time-dilated relative to the traveler! 1. 8 yrs – Similarly, during our 3 -year return trip, • we only see another 1. 8 years go by on Earth. • But, when we turn around to head back, – we change reference frames, • The change in reference frame means that when we go to the new frame, we suddenly consider a date on Earth that’s 10 − 3. 6 = 6. 4 years later than before to be “now. ” • Another example of this: – If I walk at 3 m/s towards a galaxy 100 million lightyears away, the points I label “now” in that galaxy suddenly are points a year later in the galaxy’s history… 6. 4 yrs 1. 8 yrs • If I walk in the other direction, my “now” shifts to points a year earlier. 1/25/2022 M. Frank, "Physical Limits of Computing" 44

Mixed-Frame Version of Lorentz Transformation • Usual version (with c=1): • Letting (x. A, t. A)=(x, t′) and (x. B, t. B)=(x′, t), and solving for (x. A, t. A), we get: • Or, in matrix form: (Where θ = arctan v. T) • The Lorentz transform is thus revealed as a simple rotation of the mixed-frame coordinates by angle θ! 1/25/2022 M. Frank, "Physical Limits of Computing" 45

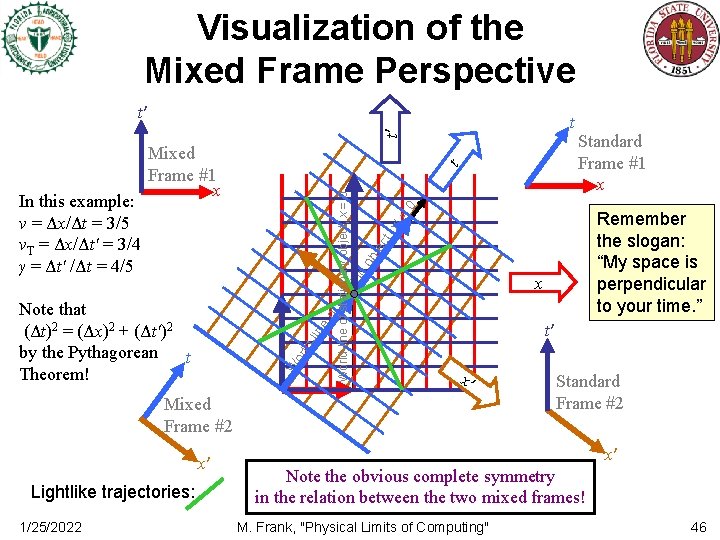
Visualization of the Mixed Frame Perspective t′ t′ t t 0 ′= t, x jec x eo lin ldor W t′ x′ Mixed Frame #2 x′ Lightlike trajectories: 1/25/2022 Remember the slogan: “My space is perpendicular to your time. ” f Note that (Δt)2 = (Δx)2 + (Δt′)2 by the Pythagorean t Theorem! Standard Frame #1 x ob ing mo World-line of stationary object, x = 0 v In this example: v = Δx/Δt = 3/5 v. T = Δx/Δt′ = 3/4 γ = Δt′ /Δt = 4/5 Mixed Frame #1 x Standard Frame #2 x′ Note the obvious complete symmetry in the relation between the two mixed frames! M. Frank, "Physical Limits of Computing" 46

Relativistic Kinetic Energy • Total relativistic energy E of any object is E = mc 2. • For an object at rest with mass m 0, Erest = m 0 c 2. • For a moving object, m = m 0/γ – Where m 0 is the object’s mass in its rest frame. • Energy of the moving object is thus Emoving = m 0 c 2/γ. • Kinetic energy Ekin : ≡ Emoving − Erest = m 0 c 2/γ − m 0 c 2 = Erest(1/γ − 1) • Substituting γ = (1−β 2)1/2 and Taylor-expanding gives: Pre-relativistic kinetic energy ½ m 0 v 2 1/25/2022 Higher-order relativistic corrections M. Frank, "Physical Limits of Computing" 47

Spacetime Intervals • Note that the lengths and times between two events are not invariant under Lorentz transformations. • However, the following quantity is a Lorentz invariant: The spacetime interval s, where: s 2 = (ct)2 − xi 2 • The value of s is also the proper time τ: – The elapsed time in rest frame of object traveling on a straight line between the two events. (Same as what we were calling t′ earlier. ) • The sign of s 2 has a particular significance: s 2 > 0 - Events are timelike separated (s is real) The events may be causally connected. s 2 = 0 - Events are lightlike separated (s is 0) Only 0 -rest-mass signals may connect them. s 2 < 0 - Events are spacelike separated (s is imaginary) The events are not causally connected at all. 1/25/2022 M. Frank, "Physical Limits of Computing" 48

Relativistic Momentum • The relativistic momentum p = mv – Same as classical momentum, except that m = m 0/γ. • Relativistic energy-momentum-rest-mass relation: E 2 = (pc)2 + (m 0 c 2)2 If we use units where c = 1, this simplifies to just: E 2 = p 2 + m 0 2 • Note that if we solve this for m 02, we get: m 0 2 = E 2 − p 2 • Thus, E 2 − p 2 is another relativistic invariant! – Later we will show it relates to the spacetime interval s 2 = t 2 − x 2, and to a computational interpretation of relativistic physics. 1/25/2022 M. Frank, "Physical Limits of Computing" 49

Topics not yet Covered • Other topics to be added to special relativity section, eventually: – Mathematical conveniences: • • • Tensors. Index notation. Covariant and contravariant tensors. 4 -vectors. Spacetime metrics. – “Momenergy” • (or, the relativistic energy-momentum 4 -vector) 1/25/2022 M. Frank, "Physical Limits of Computing" 50

Subsection II. B. 3. b: Some Tidbits on General Relativity Equivalence Principle, Curved Spacetime, Black Holes SLIDES NOT YET WRITTEN M. Frank, "Physical Limits of Computing"