FAMUFSU College of Engineering EEL 3705 3705 L

FAMU-FSU College of Engineering EEL 3705 / 3705 L Digital Logic Design Fall 2006 Instructor: Dr. Michael Frank Module #5: Combinational Logic Optimization (Thanks to Dr. Perry for the slides) 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 1

FAMU-FSU College of Engineering Wednesday, October 4, 2006 o Administrivia: n Midterm #1 grades posted, handing papers back today o n This week’s lab: o n o o “Top secret code display” (w. K-maps) Design project #1: Due this Friday!! o n Averages: 96%, 89%, 96% (98. 5 points overall) Test your designs at end of lab period, or in TA office hours Don’t delay writing the large required amount of documentation! Homework assignment #3: To be posted very soon, watch for it. Plan for today: n n Go over midterm solutions briefly Start in on next lecture topic, 3. 5: o Techniques for Combinational Logic Optimization n 3/3/2021 Emphasis on use of Karnaugh maps M. Frank, EEL 3705 Digital Logic, Fall 2006 2

FAMU-FSU College of Engineering Topic 3. 5: Techniques for Combinational Logic Optimization 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 3

FAMU-FSU College of Engineering Topic 3. 5 – Minimizing Circuits Subtopics: o 3. 5. 1. Simplification using Boolean identities n o 3. 5. 2. Karnaugh Maps (CIO #5) n o o Not covering in depth this semester in lecture Focus of this lecture 3. 5. 3. Don’t care conditions 3. 5. 4. The Quine-Mc. Cluskey Method 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 4

FAMU-FSU College of Engineering Goals of Circuit Minimization o (1) Minimize the number of primitive Boolean logic gates needed to implement the circuit. n Ultimately, this also roughly minimizes the number of transistors, the chip area, and the cost. o Also roughly minimizes the energy expenditure n n o This will be our focus. (2) It is also often useful to minimize the number of combinational stages or logical depth of the circuit. n o among traditional irreversible circuits. This roughly minimizes the delay or latency through the circuit, the time between input and output. Note: Goals (1) and (2) are often conflicting! n 3/3/2021 In the real world, a designer may have to analyze and optimize some complex trade-off between logic complexity and latency. M. Frank, EEL 3705 Digital Logic, Fall 2006 5

FAMU-FSU College of Engineering Minimizing DNF Expressions o Using DNF (or CNF) expressions guarantees that you can always find some circuit that implements any desired Boolean function. n o However, the resulting circuit may be far larger than is really required! We would like to find the smallest sum-of-products expression that is equivalent to a given function. n n 3/3/2021 This will yield a fairly small circuit. However, circuits of other forms (not either CNF or DNF) might be even smaller for complex functions. M. Frank, EEL 3705 Digital Logic, Fall 2006 6

Chapter 3 Simplification of Switching Functions 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 7

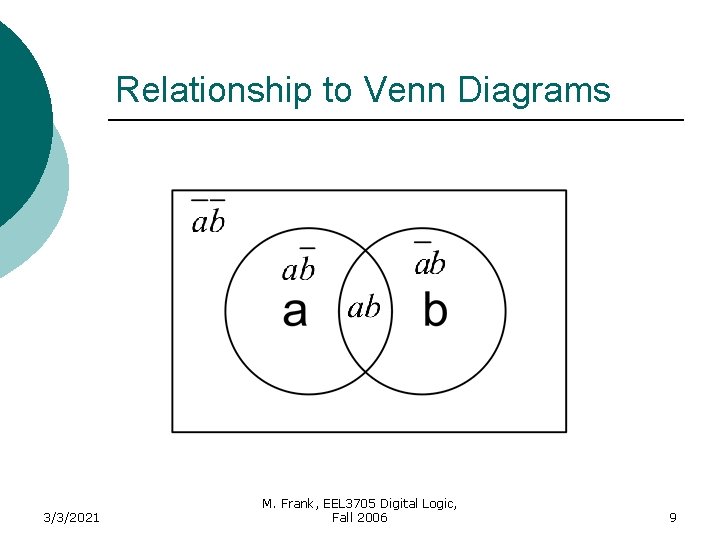
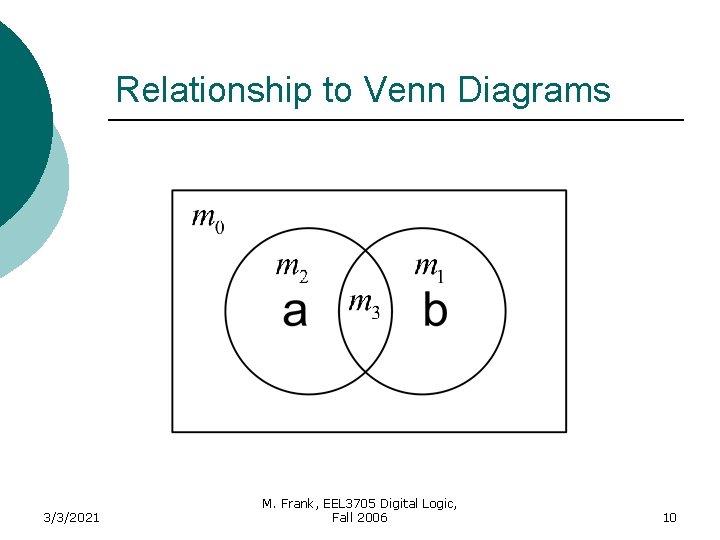
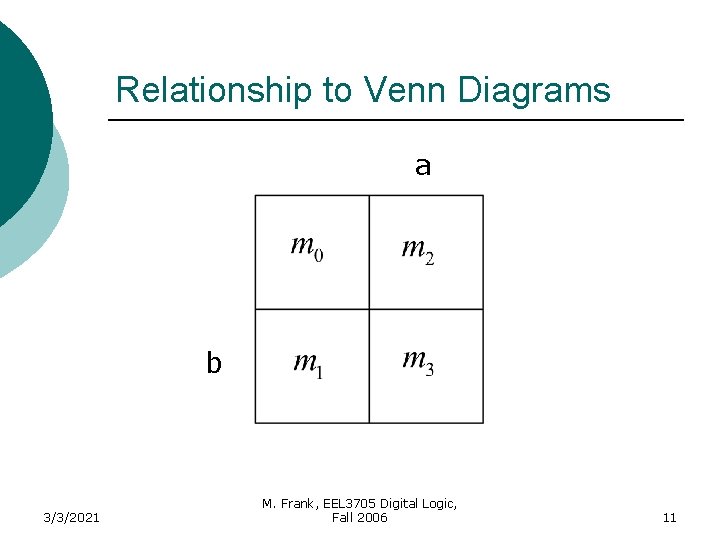
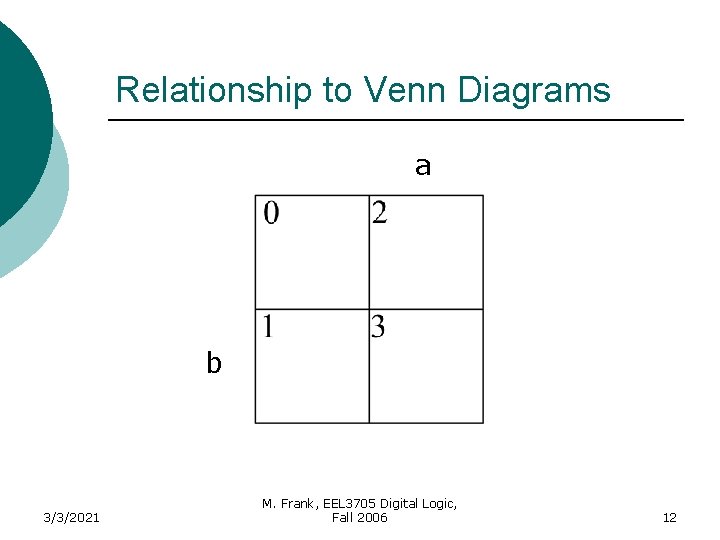
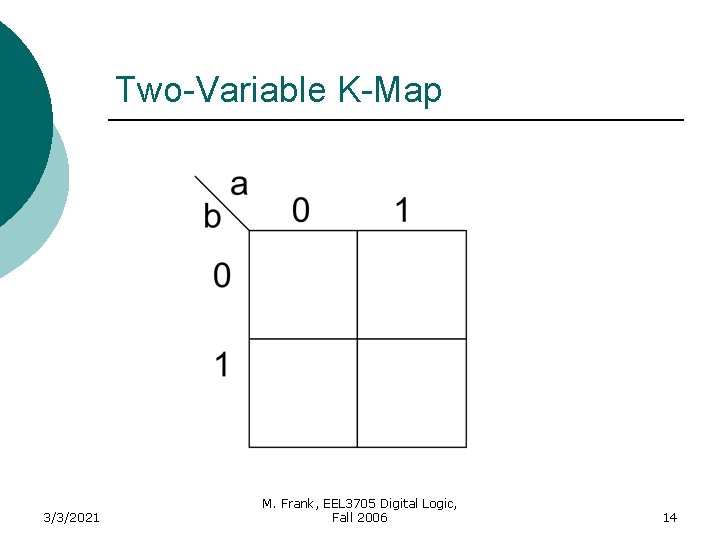
Karnaugh Maps (K-Map) A K-Map is a graphical representation of a logic function’s truth table 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 8

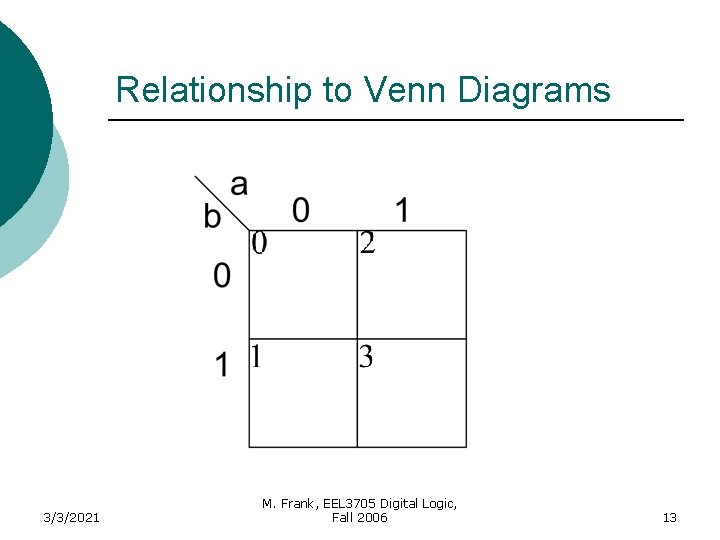
Relationship to Venn Diagrams 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 9

Relationship to Venn Diagrams 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 10

Relationship to Venn Diagrams a b 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 11

Relationship to Venn Diagrams a b 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 12

Relationship to Venn Diagrams 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 13

Two-Variable K-Map 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 14

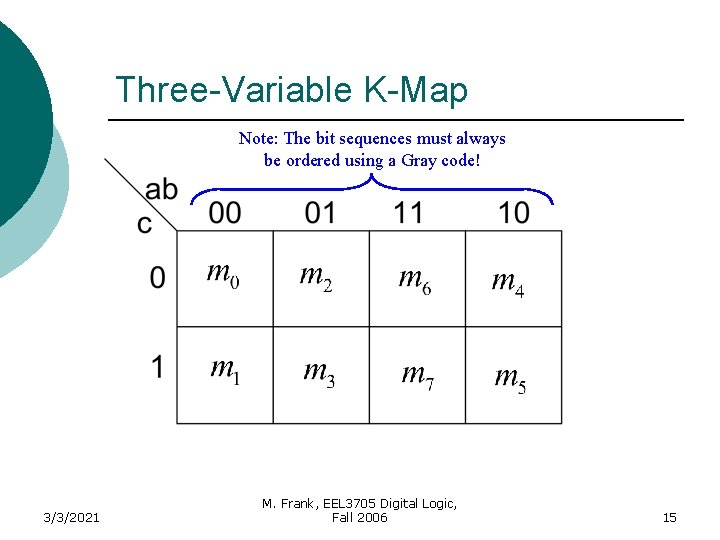
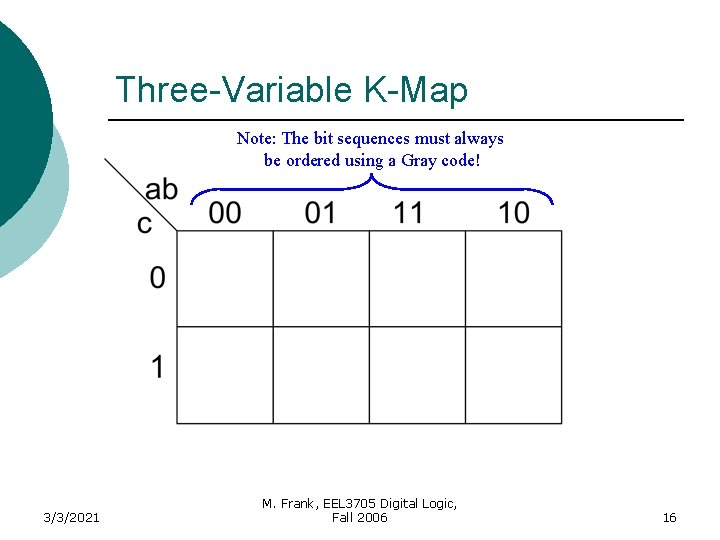
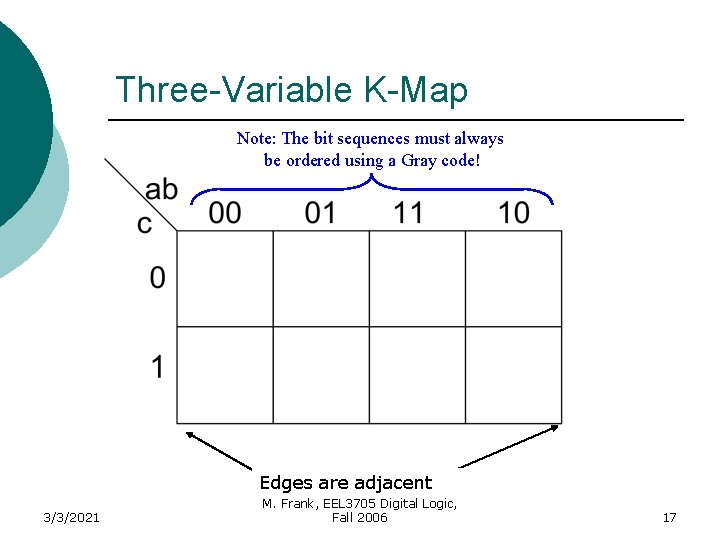
Three-Variable K-Map Note: The bit sequences must always be ordered using a Gray code! 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 15

Three-Variable K-Map Note: The bit sequences must always be ordered using a Gray code! 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 16

Three-Variable K-Map Note: The bit sequences must always be ordered using a Gray code! Edges are adjacent 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 17

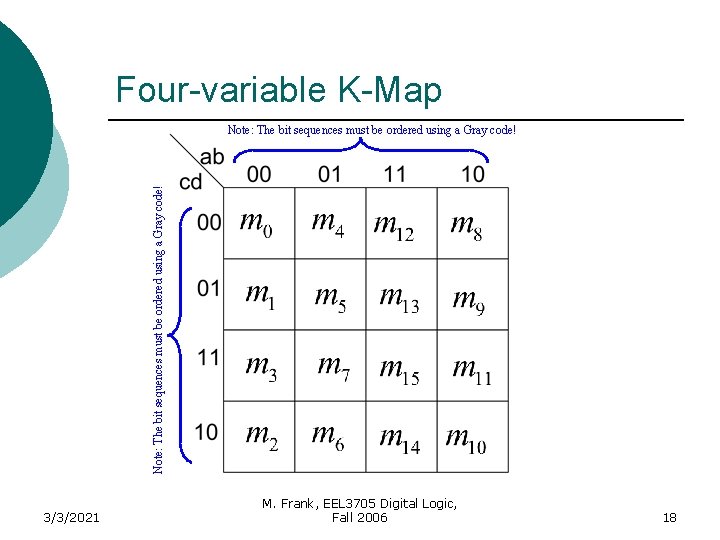
Four-variable K-Map Note: The bit sequences must be ordered using a Gray code! 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 18

Four-variable K-Map 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 19

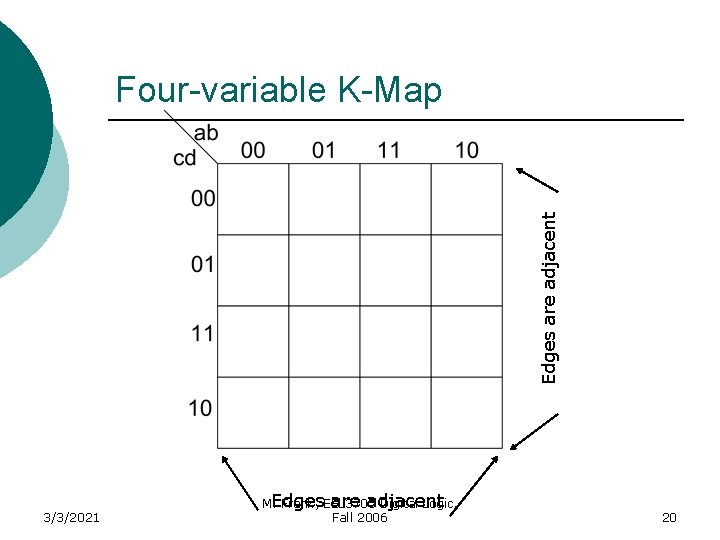
Edges are adjacent Four-variable K-Map 3/3/2021 are adjacent M. Edges Frank, EEL 3705 Digital Logic, Fall 2006 20

Plotting Functions on the K-map SOP Form 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 21

Canonical SOP Form Three Variable Example using shorthand notation 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 22

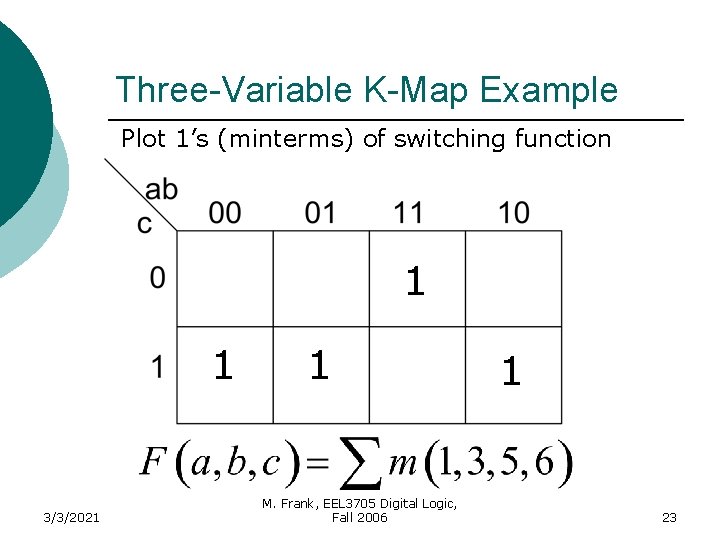
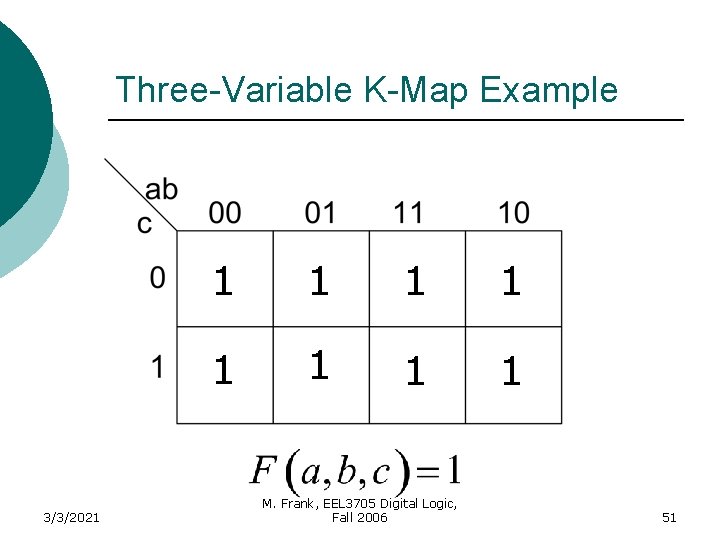
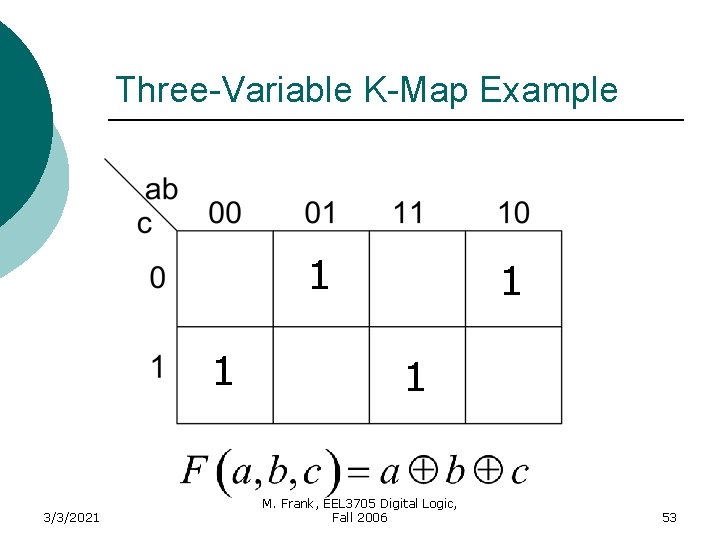
Three-Variable K-Map Example Plot 1’s (minterms) of switching function 1 1 3/3/2021 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 23

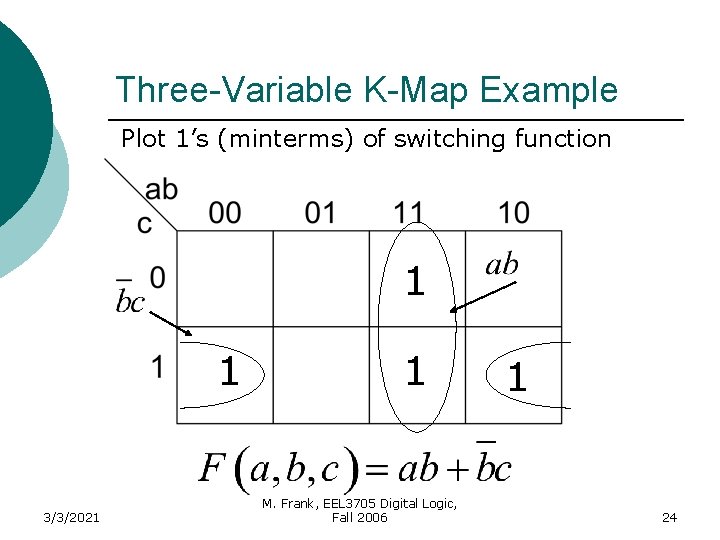
Three-Variable K-Map Example Plot 1’s (minterms) of switching function 1 1 3/3/2021 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 24

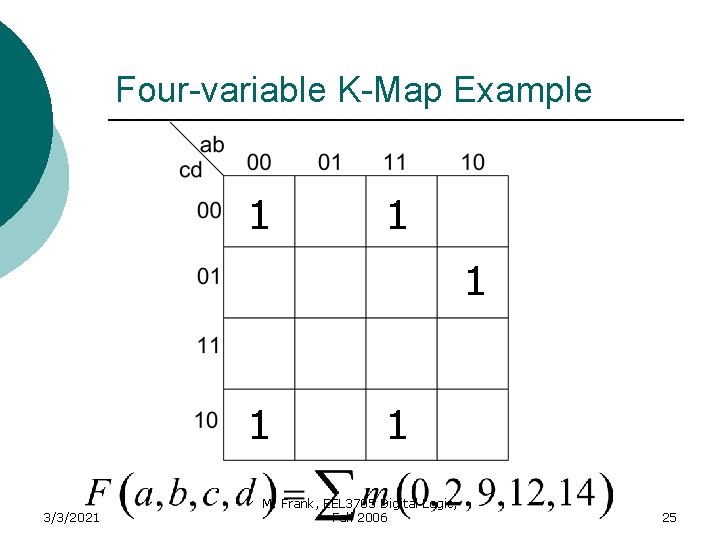
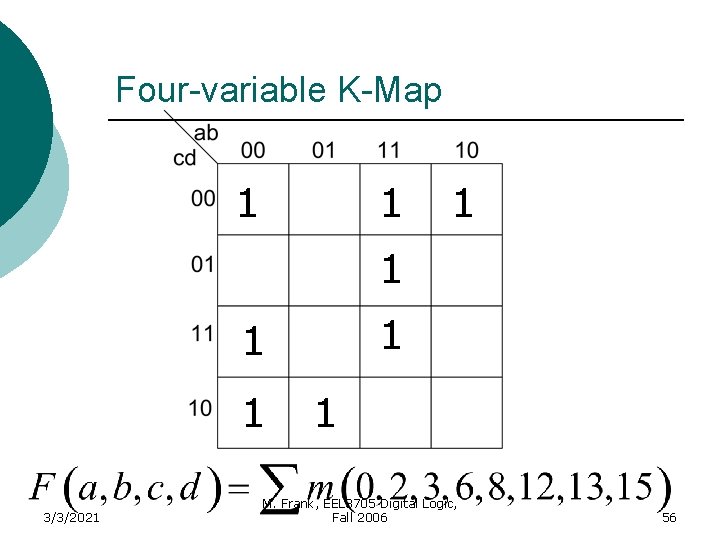
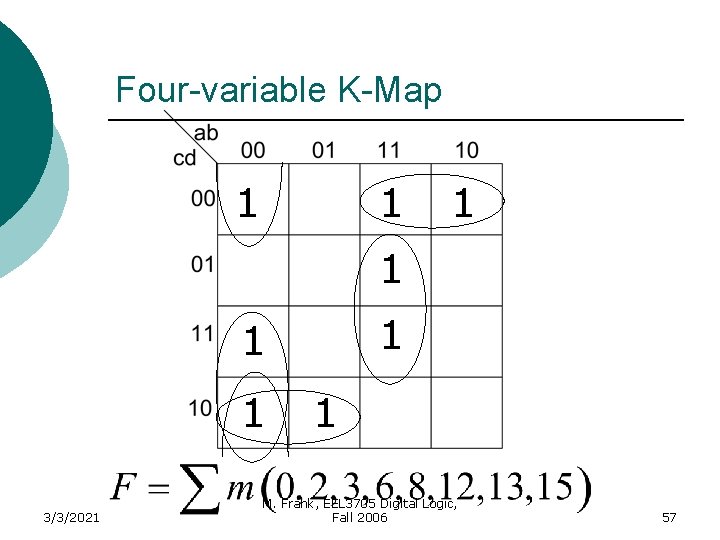
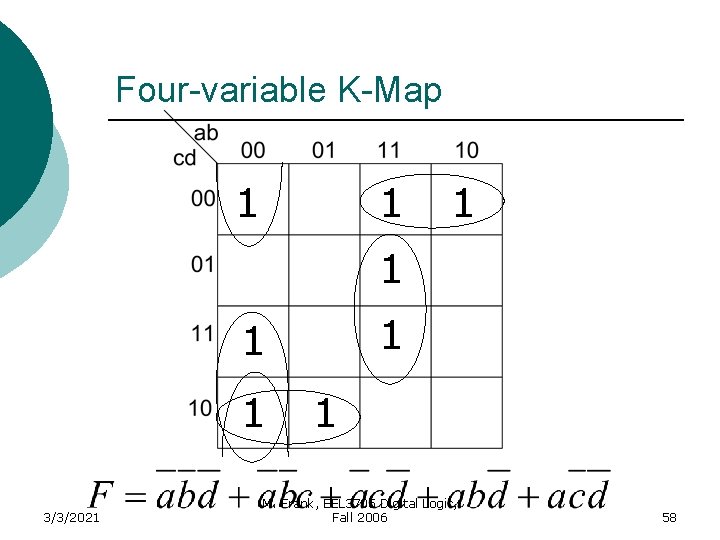
Four-variable K-Map Example 1 1 3/3/2021 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 25

Karnaugh Maps (K-Map) Simplification of Switching Functions using K-MAPS 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 26

Terminology/Definition ¡ Literal l ¡ A variable or its complement Logically adjacent terms l l Two minterms are logically adjacent if they differ in only one variable position Ex: and m 6 and m 2 are logically adjacent Note: M. Frank, EEL 3705 Digital Logic, Or, logically adjacent terms can be combined 27 3/3/2021 Fall 2006

Terminology/Definition ¡ Implicant l ¡ Prime Implicant l ¡ A prime implicant that covers at least one minterm that is not contained in another prime implicant Cover l 3/3/2021 An implicant that is not part of another implicant Essential Prime Implicant l ¡ Product term that could be used to cover minterms of a function A minterm that has been used in at least one group M. Frank, EEL 3705 Digital Logic, Fall 2006 28

Guidelines for Simplifying Functions Each square on a K-map of n variables has n logically adjacent squares. (i. e. differing in exactly one variable) ¡ When combing squares, always group in powers of 2 m , where m=0, 1, 2, …. ¡ In general, grouping 2 m variables eliminates m variables. ¡ 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 29

Guidelines for Simplifying Functions Group as many squares as possible. This eliminates the most variables. ¡ Make as few groups as possible. Each group represents a separate product term. ¡ You must cover each minterm at least once. However, it may be covered more than once. ¡ 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 30

K-map Simplification Procedure Plot the K-map ¡ Circle all prime implicants on the Kmap ¡ Identify and select all essential prime implicants for the cover. ¡ Select a minimum subset of the remaining prime implicants to complete the cover. ¡ Read the K-map ¡ 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 31

Example ¡ 3/3/2021 Use a K-Map to simplify the following Boolean expression M. Frank, EEL 3705 Digital Logic, Fall 2006 32

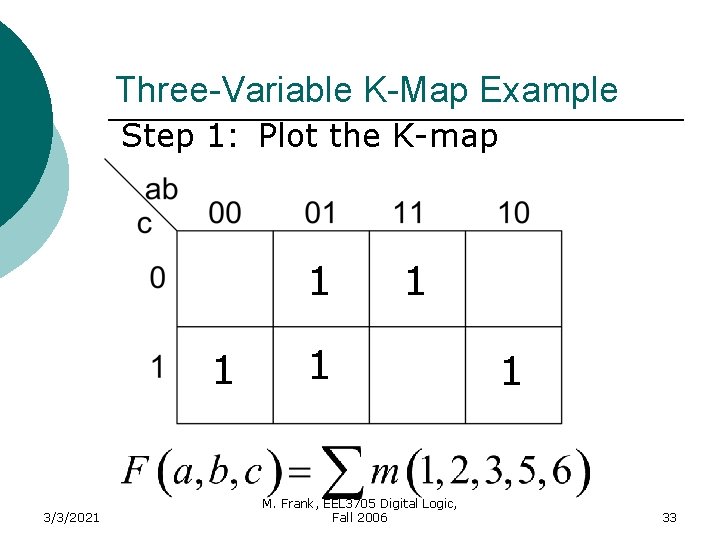
Three-Variable K-Map Example Step 1: Plot the K-map 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 33

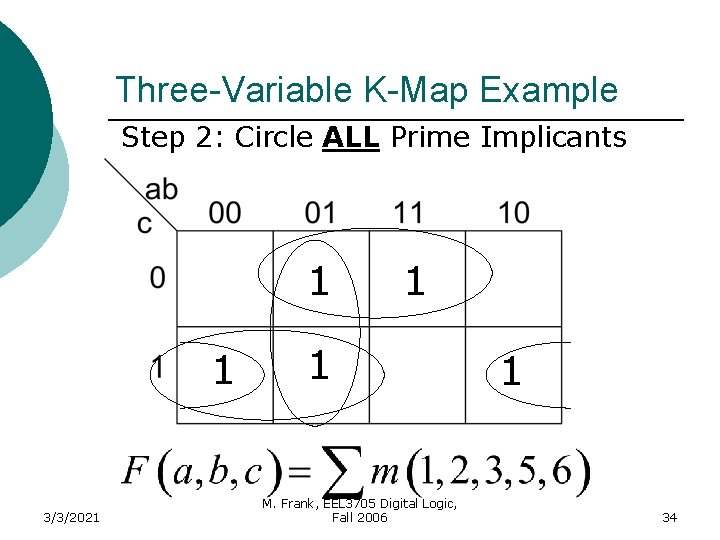
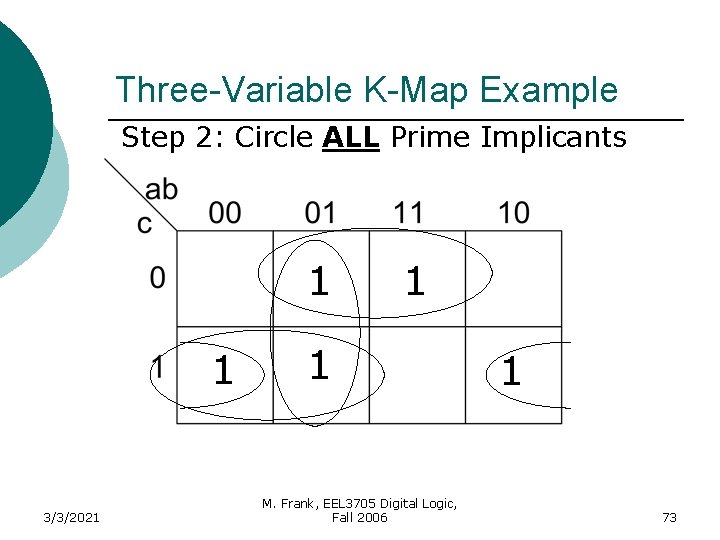
Three-Variable K-Map Example Step 2: Circle ALL Prime Implicants 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 34

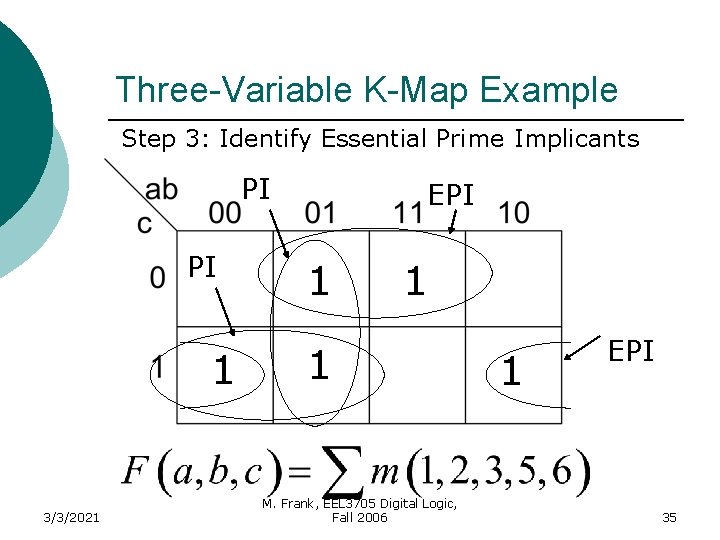
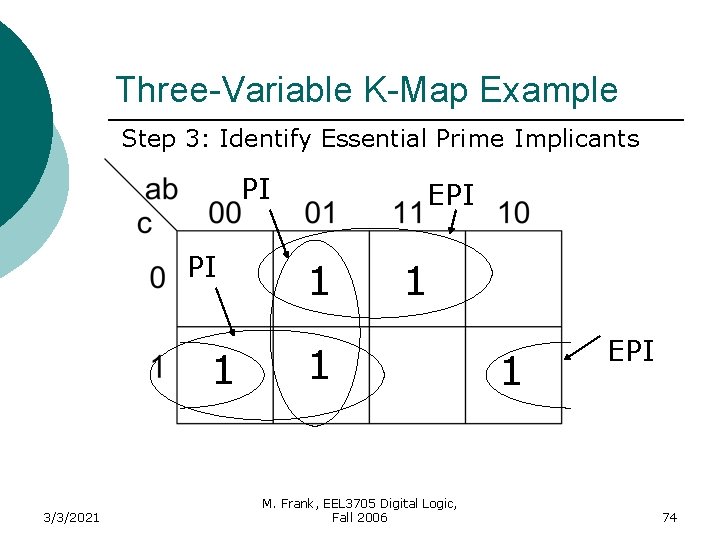
Three-Variable K-Map Example Step 3: Identify Essential Prime Implicants PI PI 1 3/3/2021 EPI 1 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 EPI 35

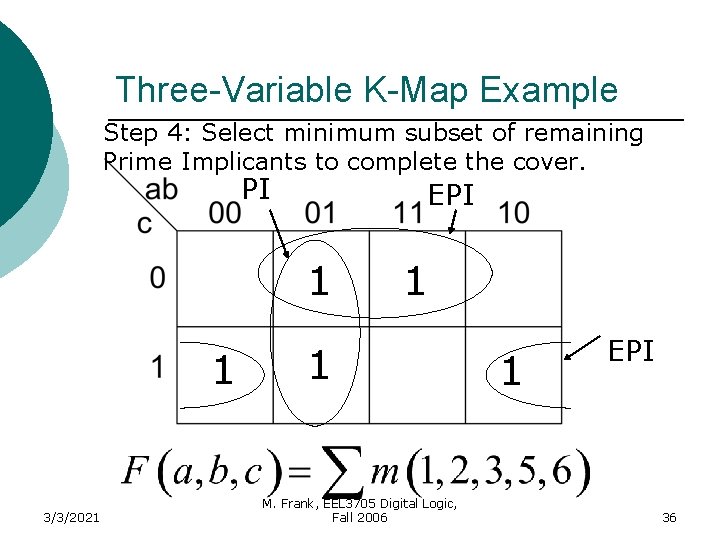
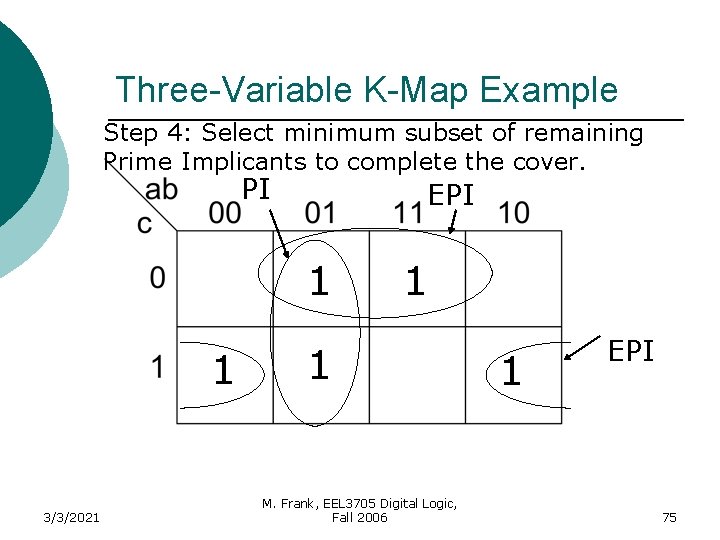
Three-Variable K-Map Example Step 4: Select minimum subset of remaining Prime Implicants to complete the cover. PI EPI 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 EPI 36

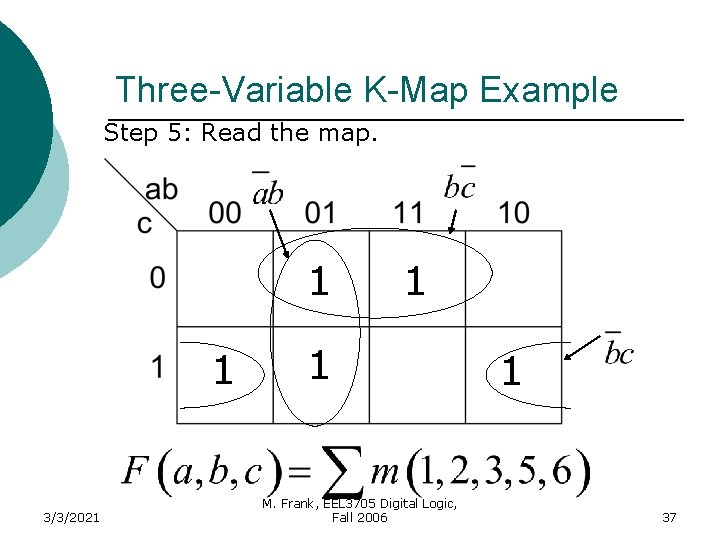
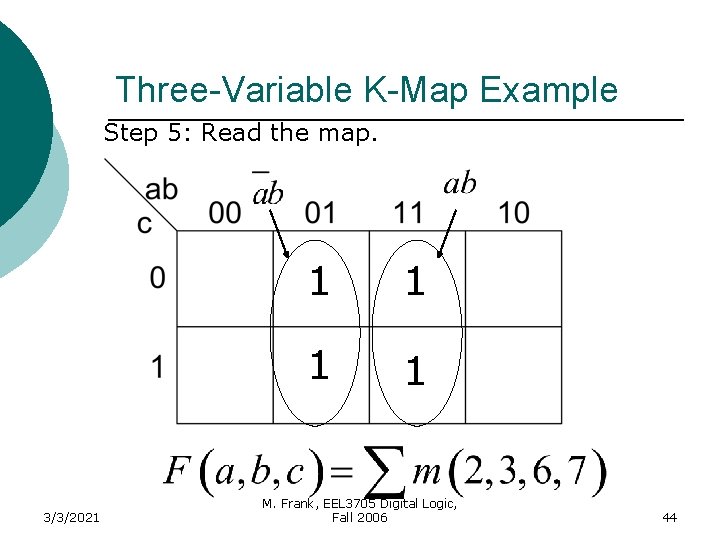
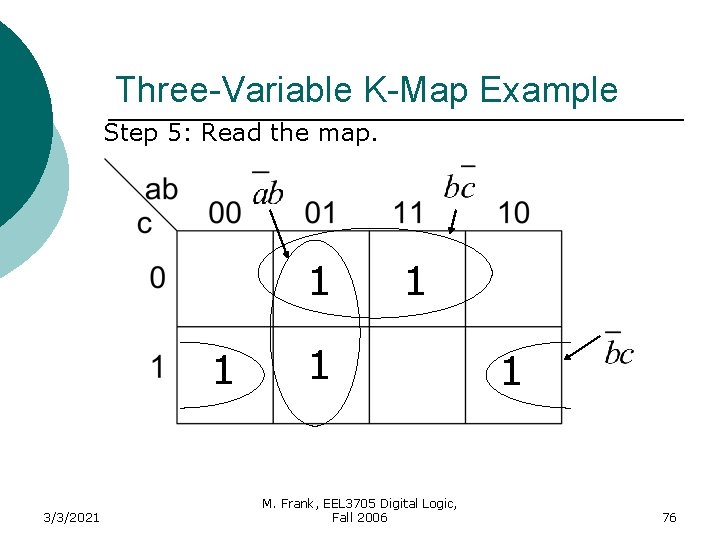
Three-Variable K-Map Example Step 5: Read the map. 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 37

Solution 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 38

Example ¡ 3/3/2021 Use a K-Map to simplify the following Boolean expression M. Frank, EEL 3705 Digital Logic, Fall 2006 39

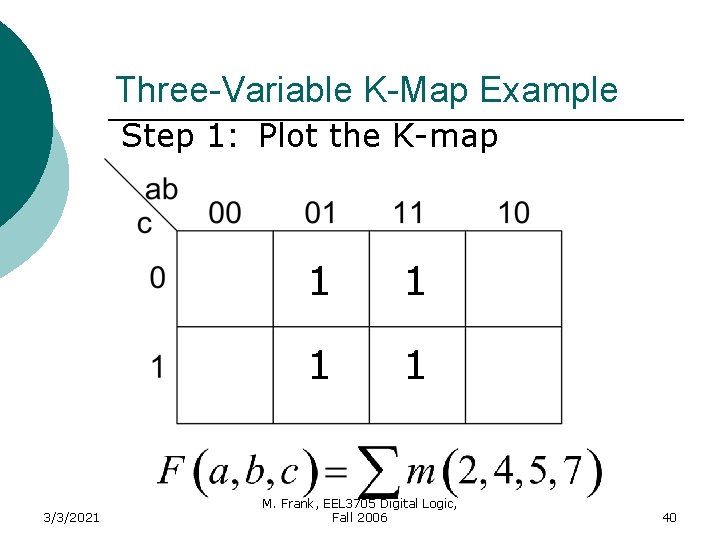
Three-Variable K-Map Example Step 1: Plot the K-map 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 40

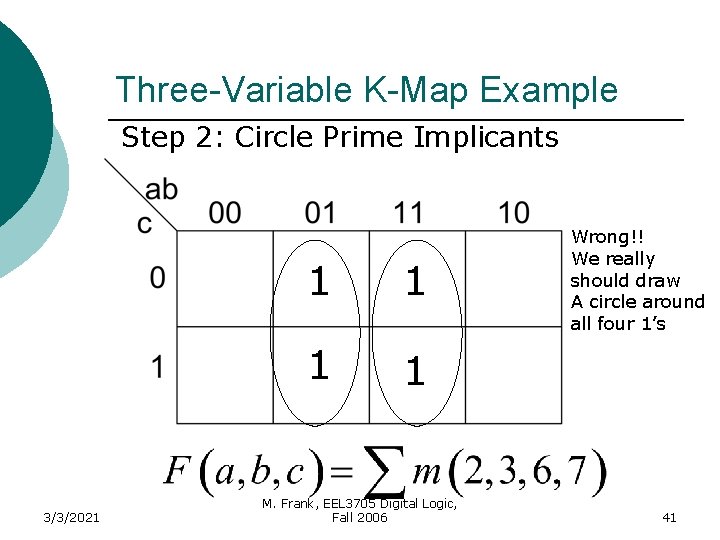
Three-Variable K-Map Example Step 2: Circle Prime Implicants 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 Wrong!! We really should draw A circle around all four 1’s 41

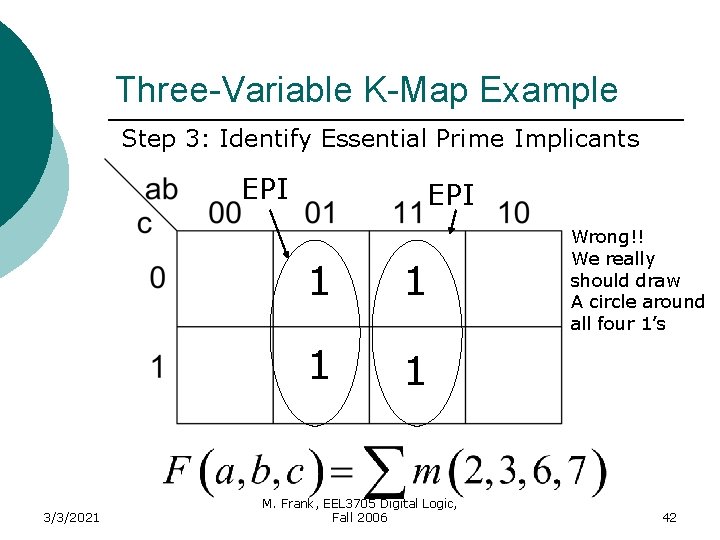
Three-Variable K-Map Example Step 3: Identify Essential Prime Implicants EPI 3/3/2021 EPI 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 Wrong!! We really should draw A circle around all four 1’s 42

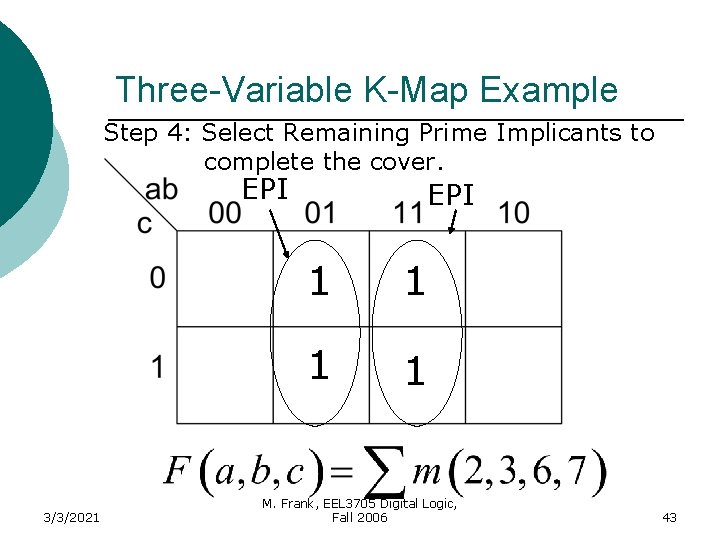
Three-Variable K-Map Example Step 4: Select Remaining Prime Implicants to complete the cover. EPI 3/3/2021 EPI 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 43

Three-Variable K-Map Example Step 5: Read the map. 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 44

Solution Since we can still simplify the function this means we did not use the largest possible groupings. 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 45

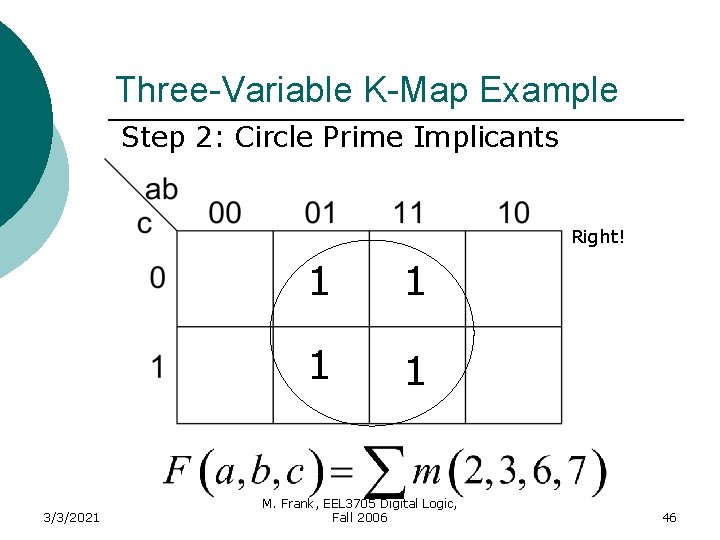
Three-Variable K-Map Example Step 2: Circle Prime Implicants Right! 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 46

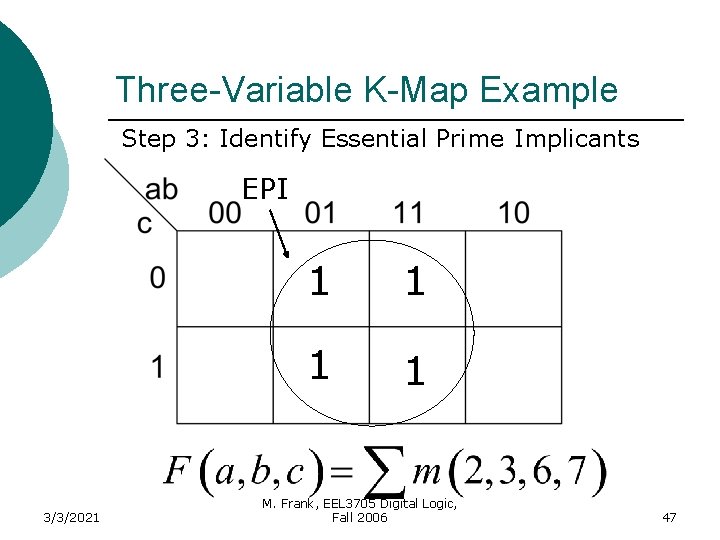
Three-Variable K-Map Example Step 3: Identify Essential Prime Implicants EPI 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 47

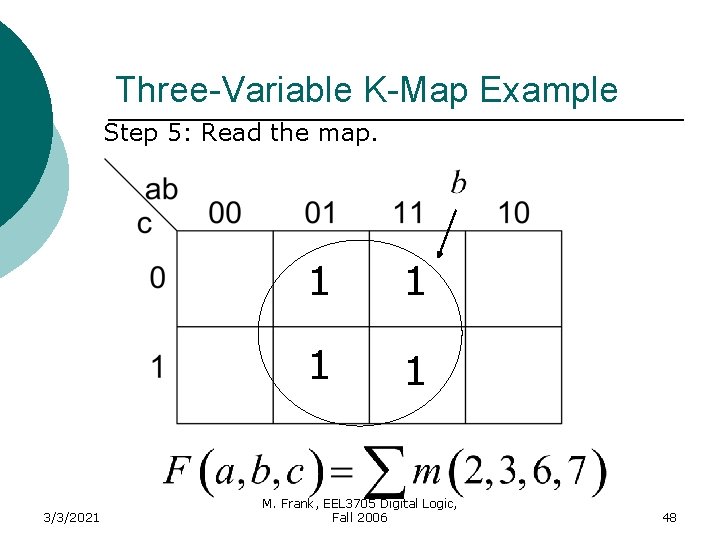
Three-Variable K-Map Example Step 5: Read the map. 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 48

Solution 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 49

Special Cases 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 50

Three-Variable K-Map Example 3/3/2021 1 1 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 51

Three-Variable K-Map Example 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 52

Three-Variable K-Map Example 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 53

Four Variable Examples 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 54

Example ¡ 3/3/2021 Use a K-Map to simplify the following Boolean expression M. Frank, EEL 3705 Digital Logic, Fall 2006 55

Four-variable K-Map 1 1 1 1 3/3/2021 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 56

Four-variable K-Map 1 1 1 1 3/3/2021 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 57

Four-variable K-Map 1 1 1 1 3/3/2021 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 58

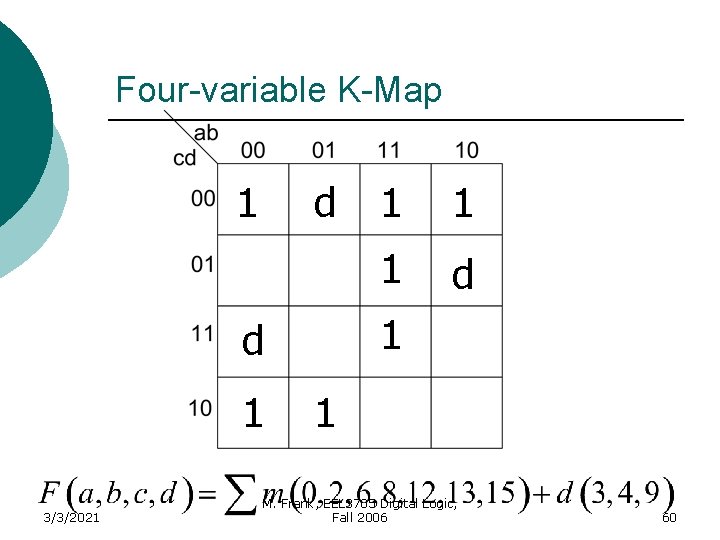
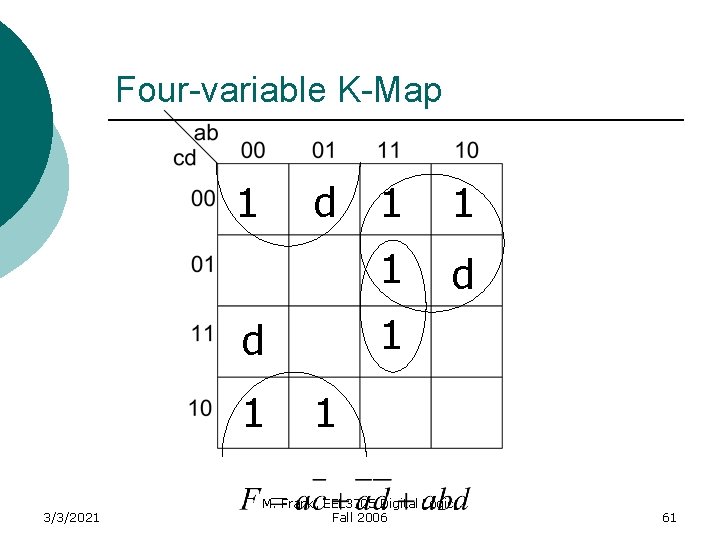
Example ¡ Use a K-Map to simplify the following Boolean expression D=Don’t care (i. e. either 1 or 0) 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 59

Four-variable K-Map 1 d 3/3/2021 1 1 d 1 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 60

Four-variable K-Map 1 d 3/3/2021 1 1 d 1 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 61

Five Variable K-Maps 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 62

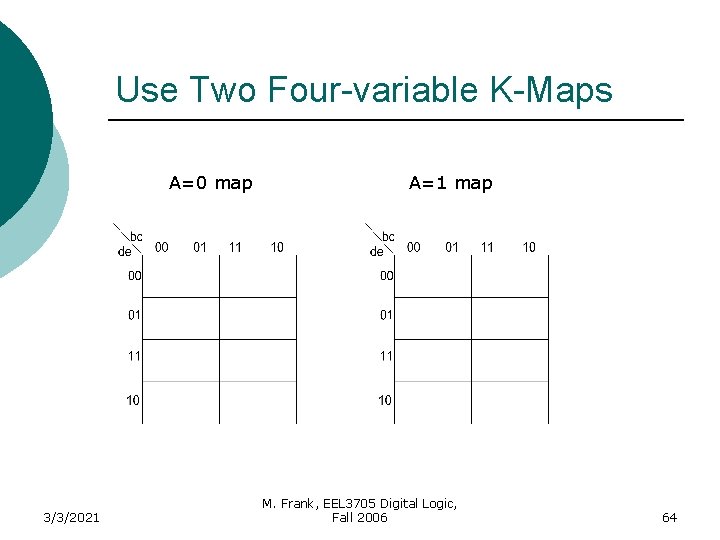
Five variable K-map Use two four variable K-maps A=1 A=0 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 63

Use Two Four-variable K-Maps A=0 map 3/3/2021 A=1 map M. Frank, EEL 3705 Digital Logic, Fall 2006 64

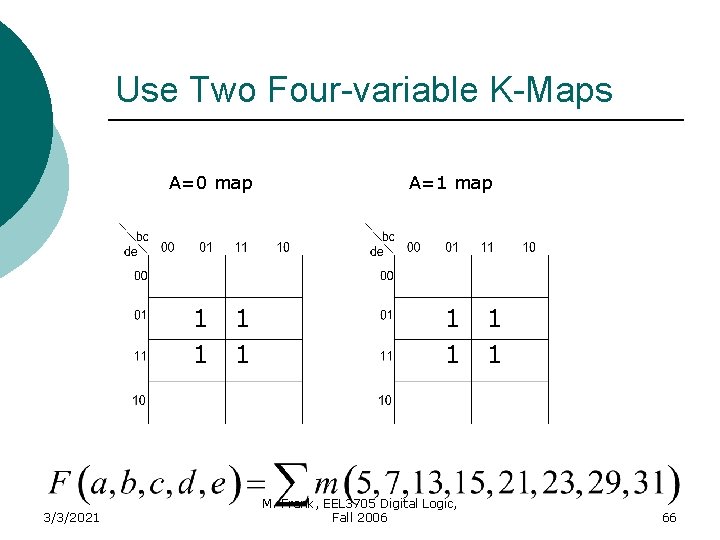
Five variable example 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 65

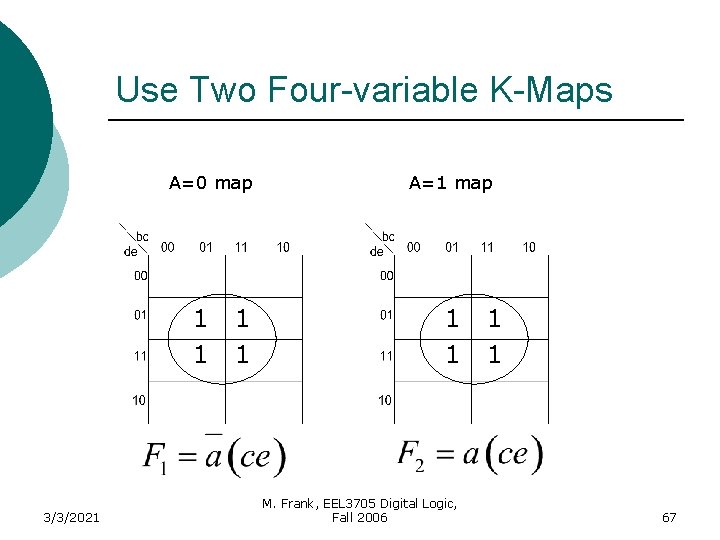
Use Two Four-variable K-Maps A=0 map 1 1 3/3/2021 1 1 A=1 map 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 1 66

Use Two Four-variable K-Maps A=0 map 1 1 3/3/2021 1 1 A=1 map 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 1 67

Five variable example 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 68

Plotting POS Functions 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 69

K-map Simplification Procedure ¡ ¡ ¡ 3/3/2021 Plot the K-map for the function F Circle all prime implicants on the K-map Identify and select all essential prime implicants for the cover. Select a minimum subset of the remaining prime implicants to complete the cover. Read the K-map Use De. Morgan’s theorem to convert F to F in POS form M. Frank, EEL 3705 Digital Logic, Fall 2006 70

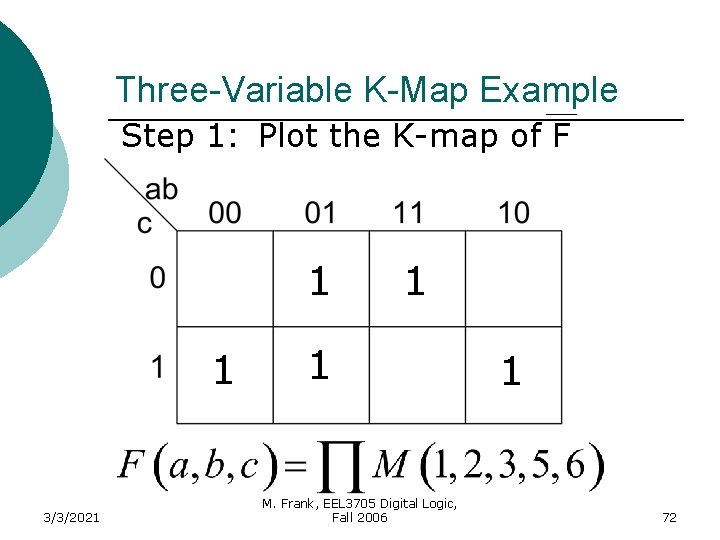
Example ¡ 3/3/2021 Use a K-Map to simplify the following Boolean expression M. Frank, EEL 3705 Digital Logic, Fall 2006 71

Three-Variable K-Map Example Step 1: Plot the K-map of F 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 72

Three-Variable K-Map Example Step 2: Circle ALL Prime Implicants 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 73

Three-Variable K-Map Example Step 3: Identify Essential Prime Implicants PI PI 1 3/3/2021 EPI 1 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 EPI 74

Three-Variable K-Map Example Step 4: Select minimum subset of remaining Prime Implicants to complete the cover. PI EPI 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 EPI 75

Three-Variable K-Map Example Step 5: Read the map. 1 1 3/3/2021 1 1 M. Frank, EEL 3705 Digital Logic, Fall 2006 1 76

Solution 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 77

TPS Quiz 3/3/2021 M. Frank, EEL 3705 Digital Logic, Fall 2006 78