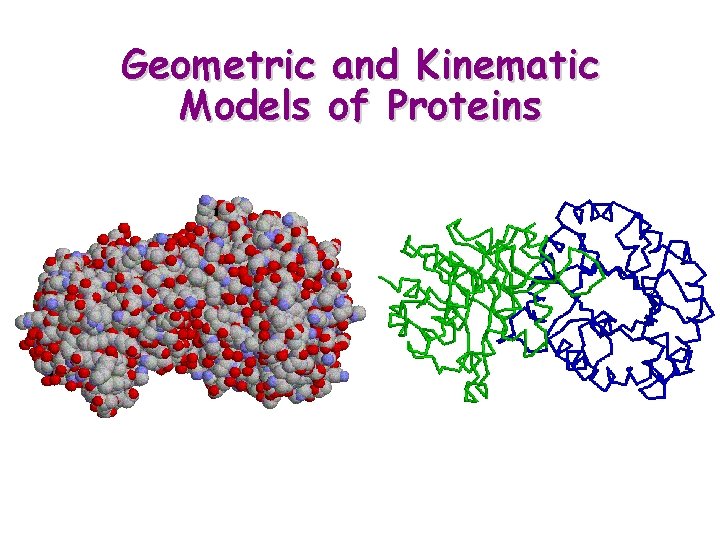
Geometric and Kinematic Models of Proteins What is





![Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects](https://slidetodoc.com/presentation_image_h2/247da1f4740d757d732d8b1c309f3670/image-12.jpg)
![Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects](https://slidetodoc.com/presentation_image_h2/247da1f4740d757d732d8b1c309f3670/image-13.jpg)




















- Slides: 73

Geometric and Kinematic Models of Proteins

What is Kinematics? Study of movement independent of the forces that cause them

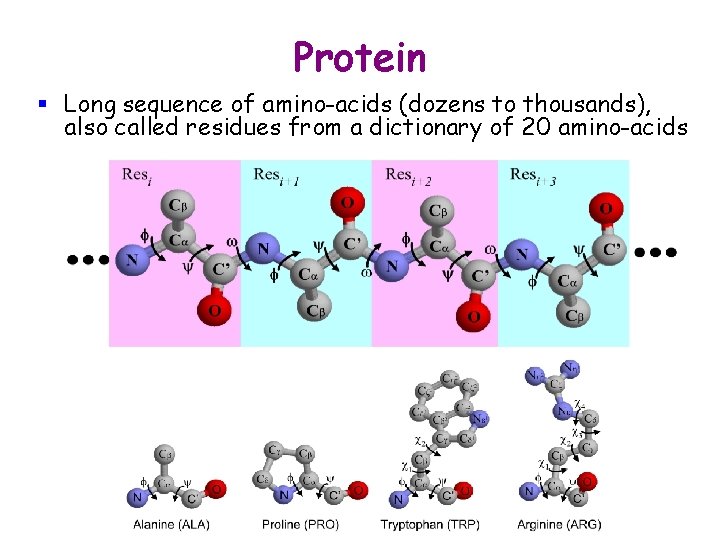
Protein § Long sequence of amino-acids (dozens to thousands), also called residues from a dictionary of 20 amino-acids

Role of Geometric and Kinematic Models § Represent the possible shapes of a protein (compare/classify shapes, find motifs) § Answer proximity queries: Which atoms are close to a given atom? (computation of energy) § Compute surface area (interaction with solvent) § Find shape features, e. g. , cavities (ligand-protein interaction)

What are the issues? § Large number of atoms Combinatorial problems § Large number of degrees of freedom Large-dimensional conformation space § Need to efficiently update information during simulation (surface area, proximity among atoms): • What is the position of every atom in some given coordinate system? • Which atoms intersect a given atom? • What atoms are within some distance range from another one? § Complex metric in conformational space § Many shape matching issues

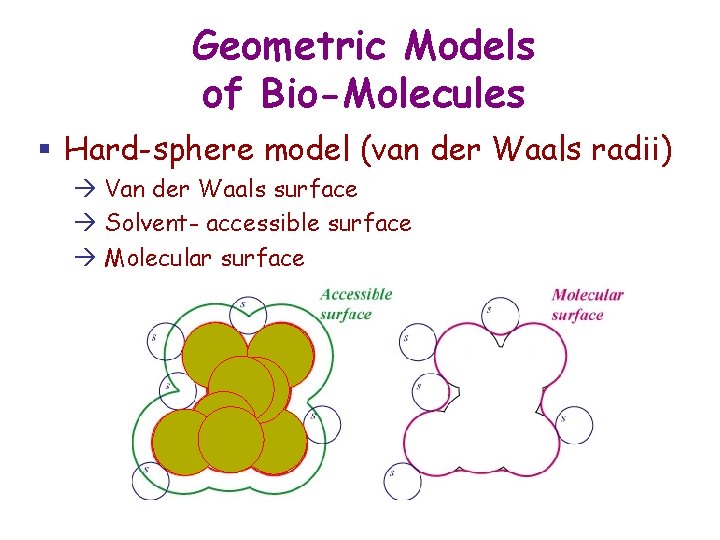
Geometric Models of Bio-Molecules § Hard-sphere model (van der Waals radii) Van der Waals surface

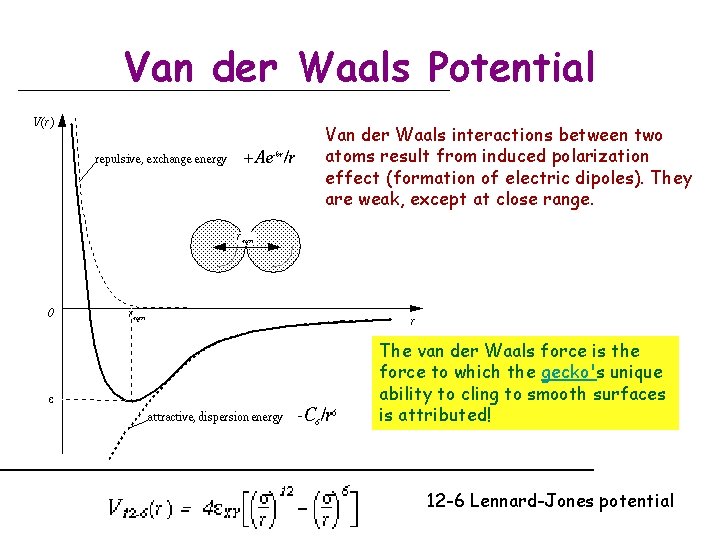
Van der Waals Potential Van der Waals interactions between two atoms result from induced polarization effect (formation of electric dipoles). They are weak, except at close range. The van der Waals force is the force to which the gecko's unique ability to cling to smooth surfaces is attributed! 12 -6 Lennard-Jones potential

Geometric Models of Bio-Molecules § Hard-sphere model (van der Waals radii) Van der Waals surface Van der Waals radii in Å H C N O F 1. 2 1. 7 1. 5 1. 4 1. 35 P S 1. 9 1. 85 Cl 1. 8

Geometric Models of Bio-Molecules § Hard-sphere model (van der Waals radii) Van der Waals surface Solvent- accessible surface Molecular surface

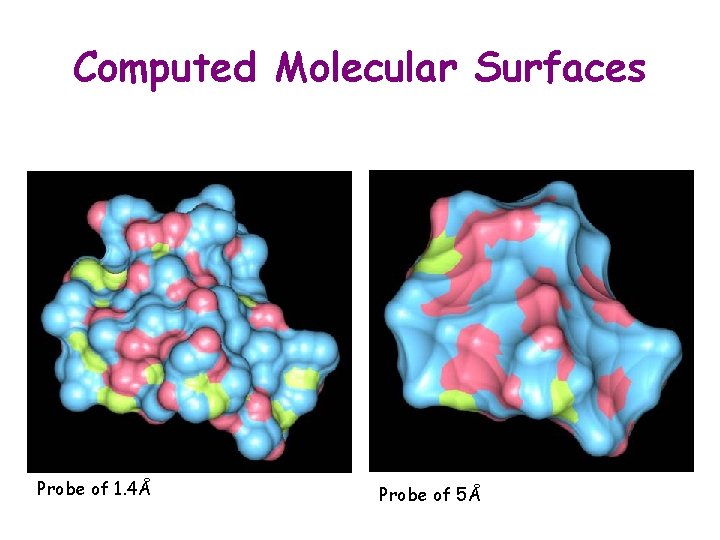
Computed Molecular Surfaces Probe of 1. 4Å Probe of 5Å

Is it art?
![Computation of HardSphere Surface Grid method Halperin and Shelton 97 Each sphere intersects Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects](https://slidetodoc.com/presentation_image_h2/247da1f4740d757d732d8b1c309f3670/image-12.jpg)
Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects O(1) Why? spheres § Computing each atom’s contribution to molecular surface takes O(1) time § Computation of molecular surface takes Θ(n) time
![Computation of HardSphere Surface Grid method Halperin and Shelton 97 Each sphere intersects Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects](https://slidetodoc.com/presentation_image_h2/247da1f4740d757d732d8b1c309f3670/image-13.jpg)
Computation of Hard-Sphere Surface (Grid method [Halperin and Shelton, 97]) § Each sphere intersects O(1) Why? spheres § Computing each atom’s contribution to D. Halperin and M. H. Overmars Spheres, molecules, and hidden surface removal molecular surface Computational Geometry: Theory and Applications 11 (2), 1998, 83 -102. takes O(1) time § Computation of molecular surface takes Θ(n) time

Trapezoidal Decomposition

Trapezoidal Decomposition D. Halperin and C. R. Shelton A perturbation scheme for spherical arrangements with application to molecular modeling Computational Geometry: Theory and Applications 10 (4), 1998, 273 -288.

Possible project: Design software to update surface area during molecule motion Other approach: Alpha shapes http: //biogeometry. duke. edu/software/alphashapes/pubs. html

Simplified Geometric Models § United-atom model: non-polar H atoms are incorporated into the heavy atoms to which they are bonded § Lollipop model: the side-chains are approximated as single spheres with varying radii § Bead model: Each residue is modeled as a single sphere

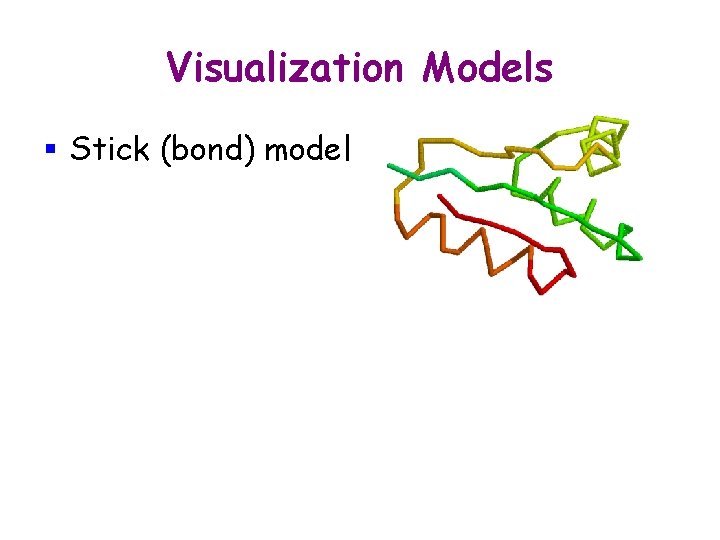
Visualization Models § Stick (bond) model


Visualization Models

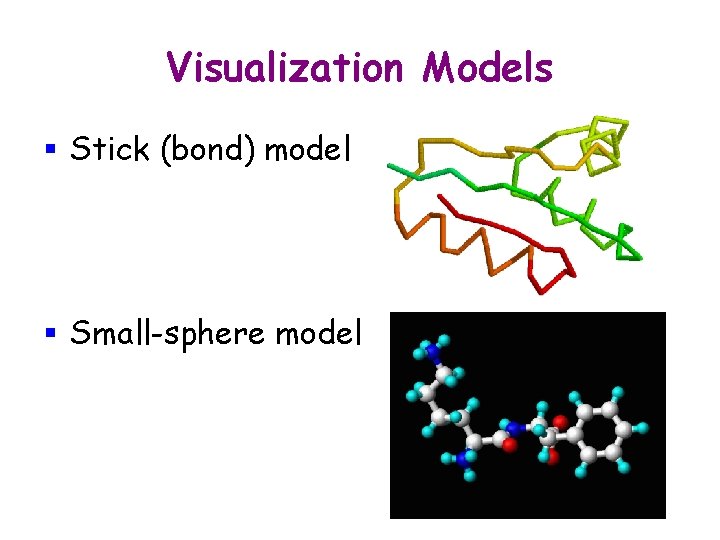
Visualization Models § Stick (bond) model § Small-sphere model

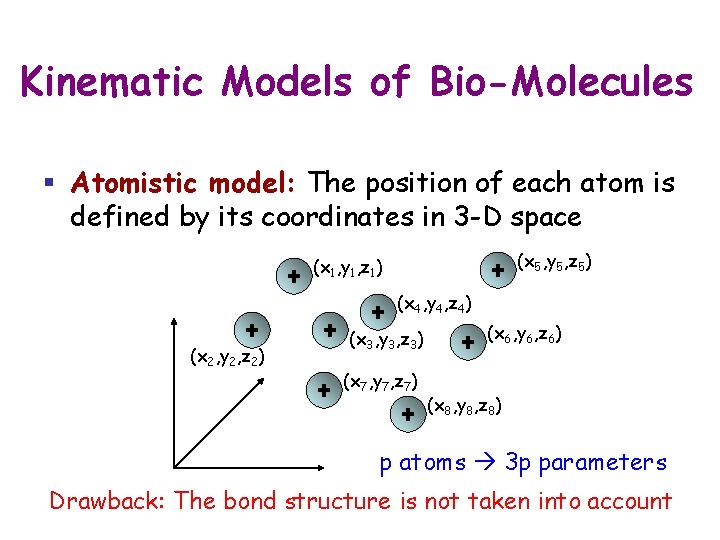
Kinematic Models of Bio-Molecules § Atomistic model: The position of each atom is defined by its coordinates in 3 -D space (x 5, y 5, z 5) (x 1, y 1, z 1) (x 4, y 4, z 4) (x 2, y 2, z 2) (x 3, y 3, z 3) (x 7, y 7, z 7) (x 6, y 6, z 6) (x 8, y 8, z 8) p atoms 3 p parameters Drawback: The bond structure is not taken into account

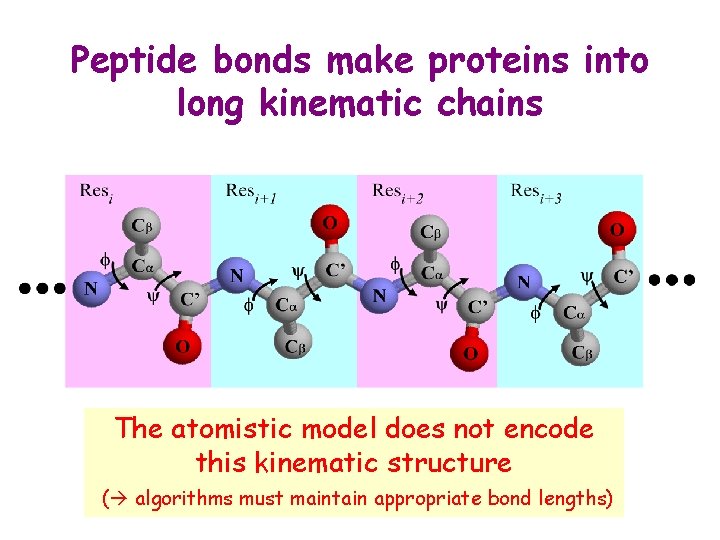
Peptide bonds make proteins into long kinematic chains The atomistic model does not encode this kinematic structure ( algorithms must maintain appropriate bond lengths)

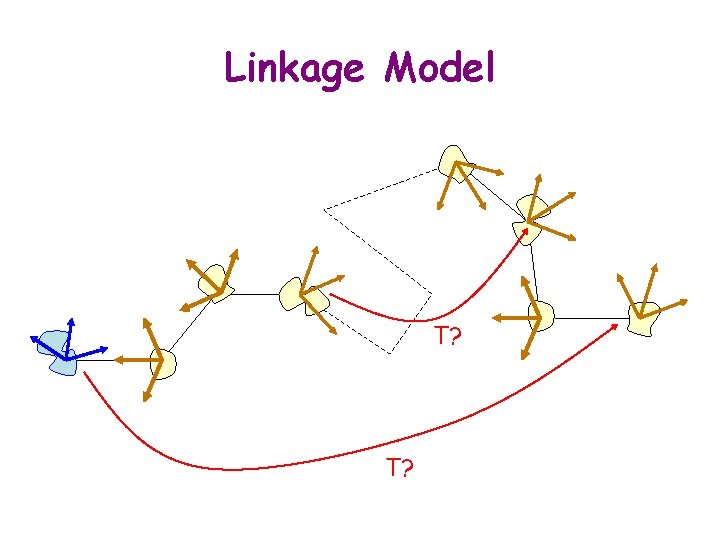
Kinematic Models of Bio-Molecules § Atomistic model: The position of each atom is defined by its coordinates in 3 -D space § Linkage model: The kinematics is defined by internal coordinates (bond lengths and angles, and torsional angles around bonds)

Linkage Model T?

Issues with Linkage Model § Update the position of each atom in world coordinate system § Determine which pairs of atoms are within some given distance (topological proximity along chain spatial proximity but the reverse is not true)

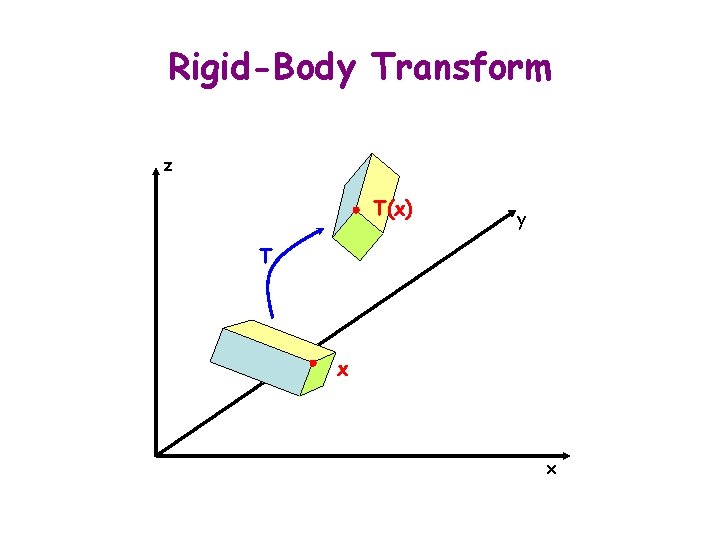
Rigid-Body Transform z T(x) y T x x

2 -D Case y x

2 -D Case yy xx

2 -D Case y y x x

y 2 -D Case y x x

2 -D Case y y x x

x 2 -D Case y y x

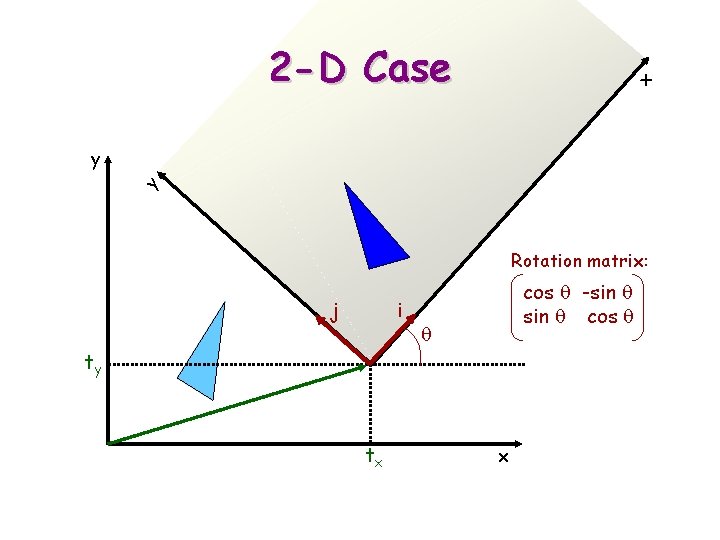
x 2 -D Case y y Rotation matrix: j i cos q -sin q cos q q ty tx x

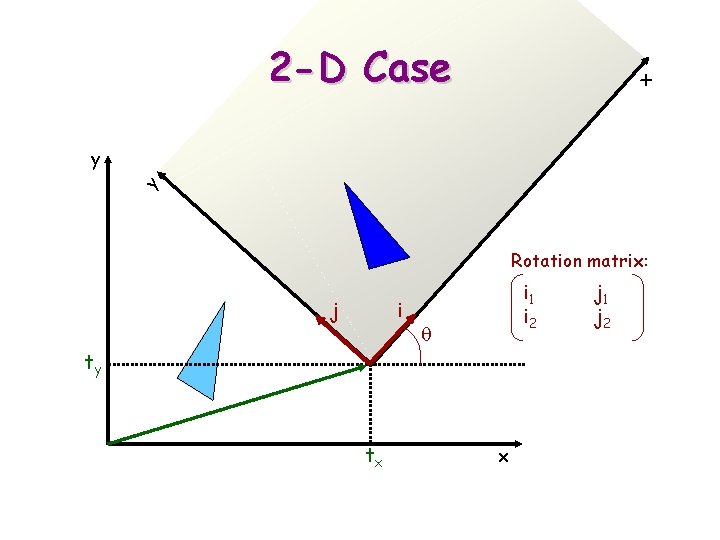
x 2 -D Case y y Rotation matrix: j i i 1 i 2 q ty tx x j 1 j 2

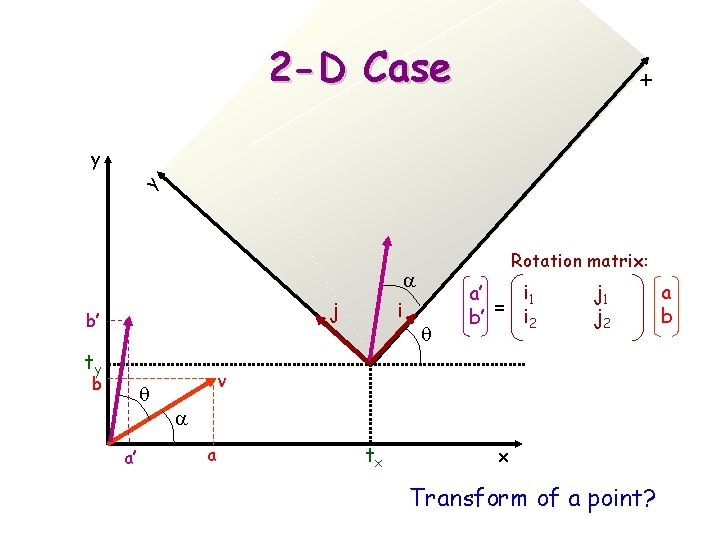
x 2 -D Case y y Rotation matrix: a j b’ ty b q a’ i q i 1 a’ b’ = i 2 j 1 j 2 v a a tx x Transform of a point? a b

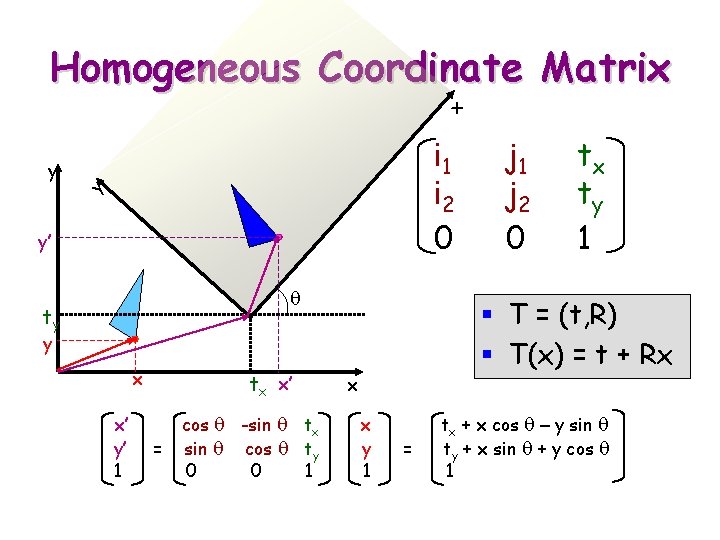
x Homogeneous Coordinate Matrix i 1 i 2 0 y y y’ q ty x’ y’ 1 tx x’ = cos q -sin q tx sin q cos q ty 0 0 1 tx ty 1 § T = (t, R) § T(x) = t + Rx y x j 1 j 2 0 x x y 1 = tx + x cos q – y sin q ty + x sin q + y cos q 1

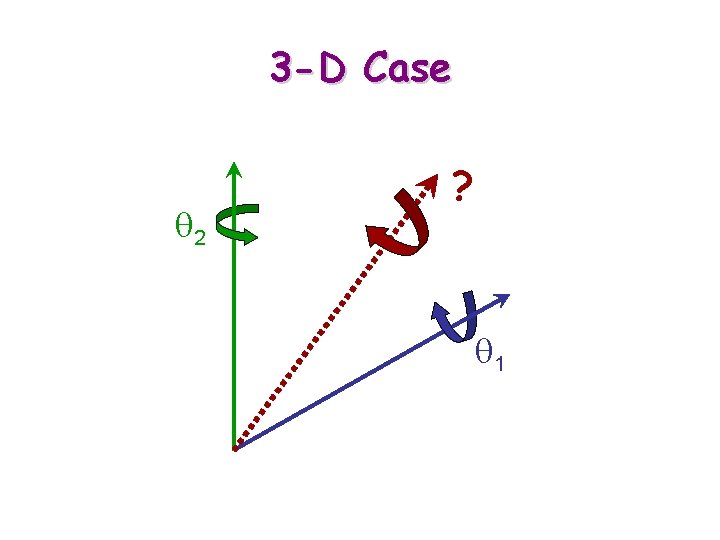
3 -D Case q 2 ? q 1

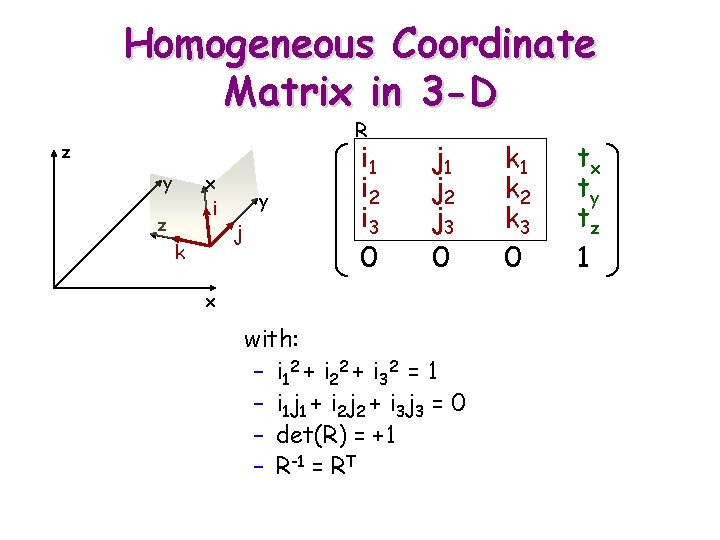
Homogeneous Coordinate Matrix in 3 -D R z y x i z k y j i 1 i 2 i 3 0 j 1 j 2 j 3 0 x with: – i 12 + i 2 2 + i 3 2 = 1 – i 1 j 1 + i 2 j 2 + i 3 j 3 = 0 – det(R) = +1 – R-1 = RT k 1 k 2 k 3 0 tx ty tz 1

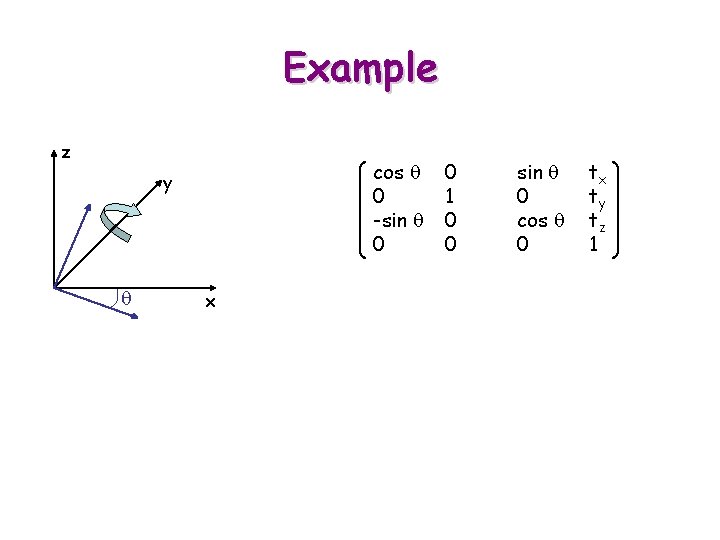
Example z cos q 0 -sin q 0 y q x 0 1 0 0 sin q 0 cos q 0 tx ty tz 1

Rotation Matrix R(k, q) = kxkxvq+ cq kxkyvq+ kzsq kxkzvq- kysq where: • k = (kx ky kz)T • sq = sinq • cq = cosq • vq = 1 -cosq kxkyvq- kzsq kykyvq+ cq kykzvq+ kxsq kxkzvq+ kysq kykzvq- kxsq kzkzvq+ cq k q

Homogeneous Coordinate Matrix in 3 -D z (x, y, z) y z (x’, y’, z’) k x i y j x’ y’ z’ = 1 i 2 i 3 0 j 1 j 2 j 3 0 k 1 k 2 k 3 0 x Composition of two transforms represented by matrices T 1 and T 2 : T 2 T 1 tx ty tz 1 x y z 1

Questions? What is the potential problem with homogeneous coordinate matrix?

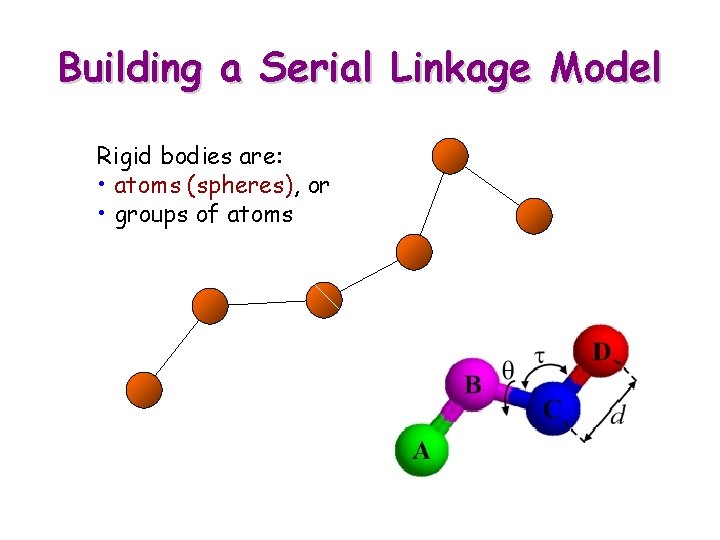
Building a Serial Linkage Model Rigid bodies are: • atoms (spheres), or • groups of atoms

Building a Serial Linkage Model 1. Build the assembly of the first 3 atoms: a. Place 1 st atom anywhere in space b. Place 2 nd atom anywhere at bond length

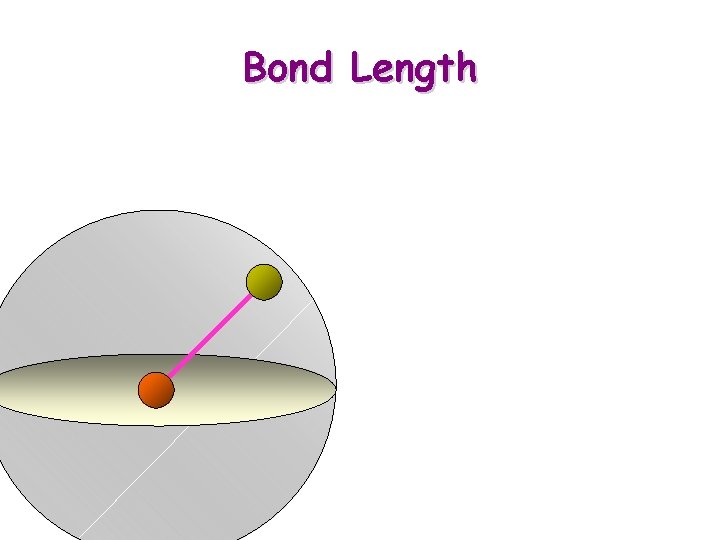
Bond Length

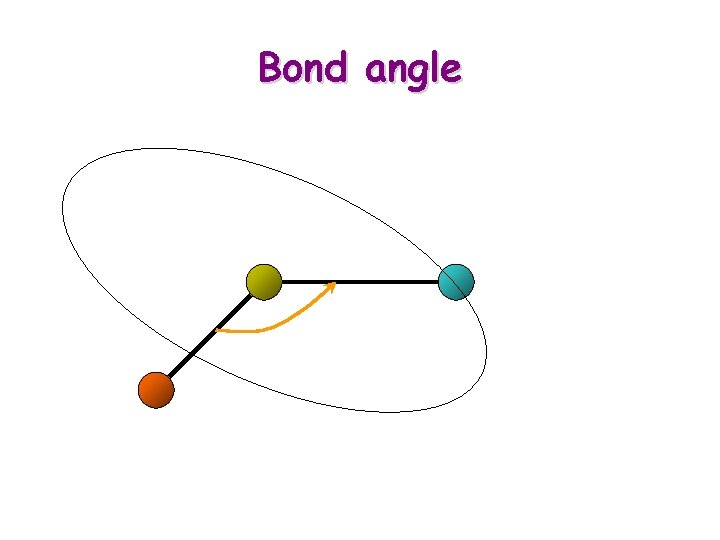
Building a Serial Linkage Model 1. Build the assembly of the first 3 atoms: a. Place 1 st atom anywhere in space b. Place 2 nd atom anywhere at bond length c. Place 3 rd atom anywhere at bond length with bond angle

Bond angle

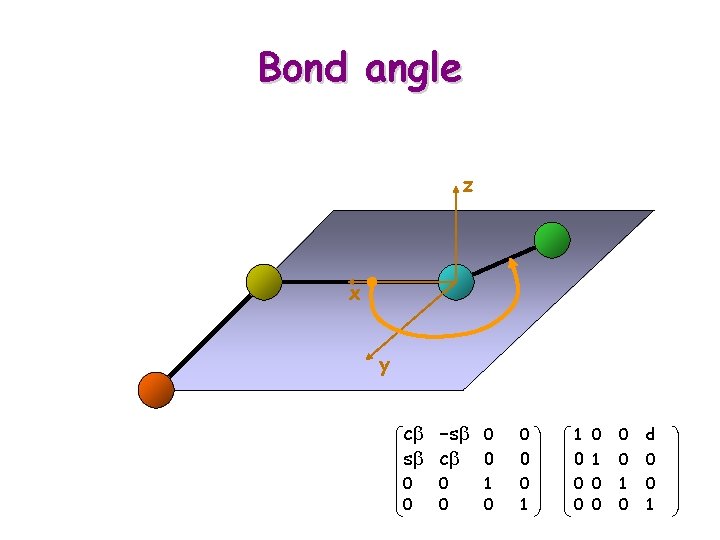
Coordinate Frame z x y

Building a Serial Linkage Model 1. Build the assembly of the first 3 atoms: a. Place 1 st atom anywhere in space b. Place 2 nd atom anywhere at bond length c. Place 3 rd atom anywhere at bond length with bond angle 2. Introduce each additional atom in the sequence one at a time

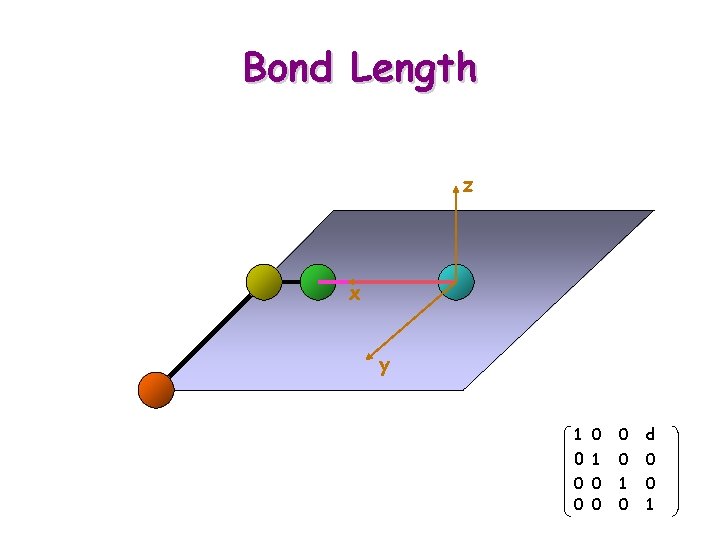
Bond Length z x y 1 Ti+1 = 0 0 0 ct -st 0 st ct 0 0 0 1 cb -sb 0 sb cb 0 0 0 1 0 0 d 0 0 1 0 0 0 1

Bond angle z x y 1 Ti+1 = 0 0 0 ct -st 0 st ct 0 0 0 1 cb -sb 0 sb cb 0 0 0 1 0 0 d 0 0 1 0 0 0 1

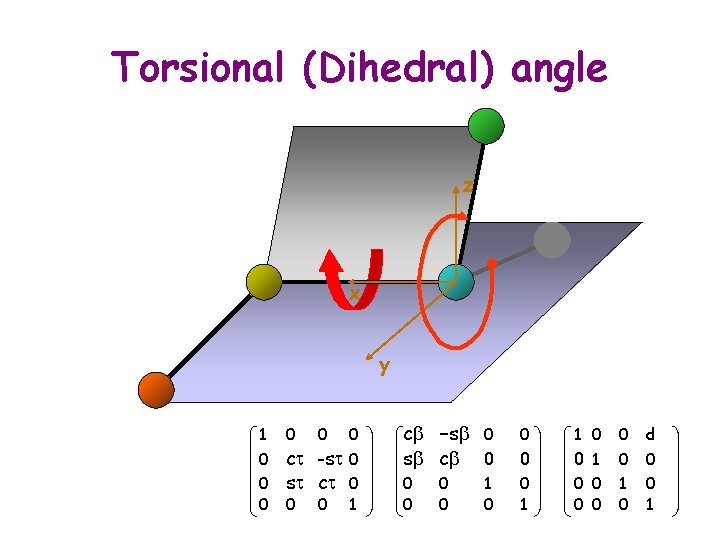
Torsional (Dihedral) angle z x y 1 Ti+1 = 0 0 0 ct -st 0 st ct 0 0 0 1 cb -sb 0 sb cb 0 0 0 1 0 0 d 0 0 1 0 0 0 1

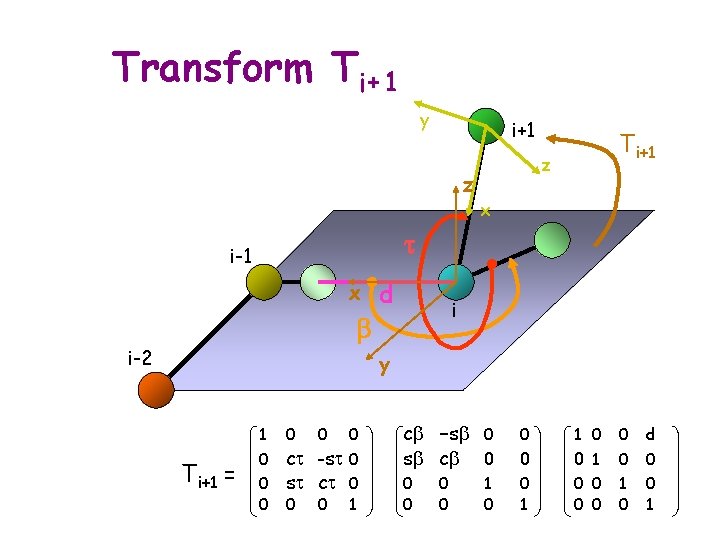
Transform Ti+1 y i+1 z Ti+1 z x t i-1 x b i-2 d i y 1 Ti+1 = 0 0 0 ct -st 0 st ct 0 0 0 1 cb -sb 0 sb cb 0 0 0 1 0 0 d 0 0 1 0 0 0 1

Transform Ti+1 y Readings: i+1 Ti+1 z J. J. Craig. Introduction to Robotics. Addison Wesley, reading, MA, z 1989. x t for Fast and Accurate Zhang, M. and Kavraki, i-1 L. E. . A New Method Derivation of Molecular Conformations. Journal of Chemical x d Information and Computer Sciences, 42(1): 64– 70, 2002. i http: //www. cs. rice. edu/CS/Robotics/papers/zhang 2002 fast-compb mole-conform. pdf i-2 y 1 Ti+1 = 0 0 0 ct -st 0 st ct 0 0 0 1 cb -sb 0 sb cb 0 0 0 1 0 0 d 0 0 1 0 0 0 1

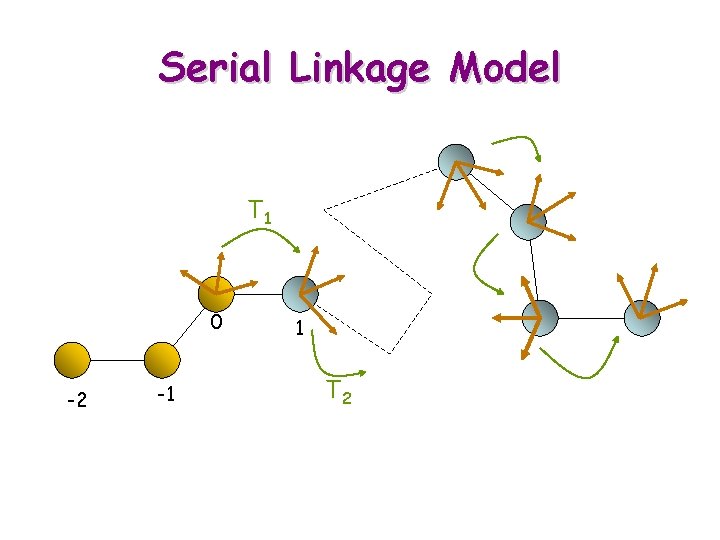
Serial Linkage Model T 1 0 -2 -1 1 T 2

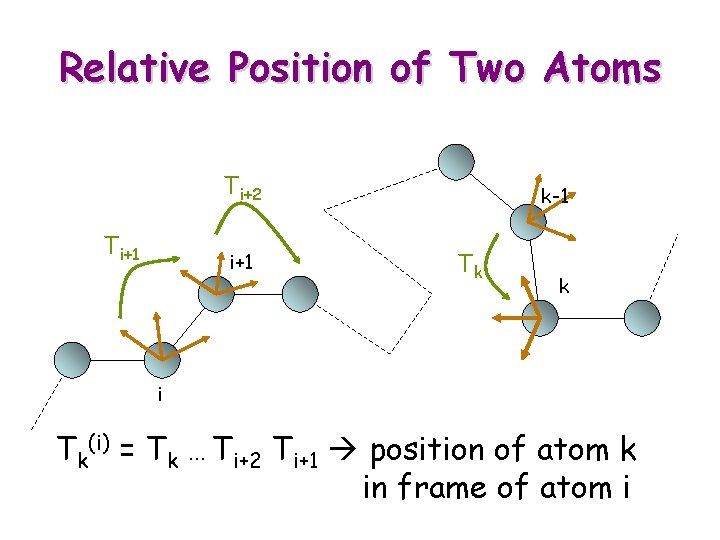
Relative Position of Two Atoms Ti+2 Ti+1 k-1 Tk k i Tk(i) = Tk … Ti+2 Ti+1 position of atom k in frame of atom i

Update § § Tk(i) = Tk … Ti+2 Ti+1 Atom j between i and k Tk(i) = Tj(i) Tj+1 Tk(j+1) A parameter between j and j+1 is changed § Tj+1 § Tk(i) = Tj(i) Tj+1 Tk(j+1)

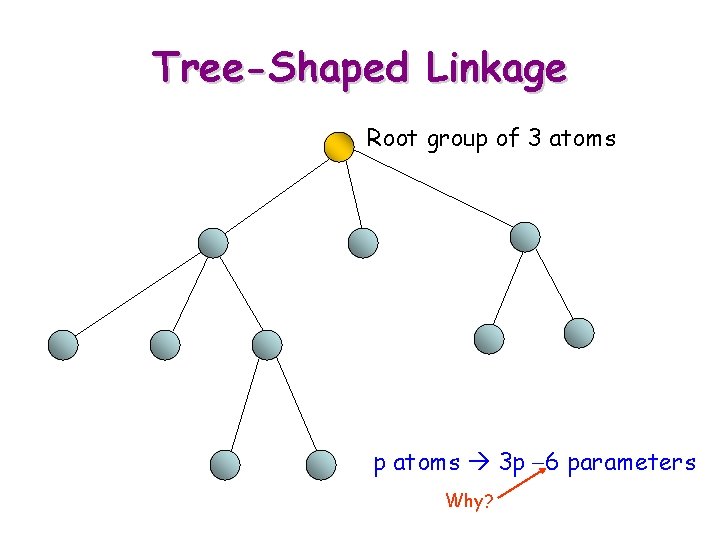
Tree-Shaped Linkage Root group of 3 atoms p atoms 3 p -6 parameters Why?

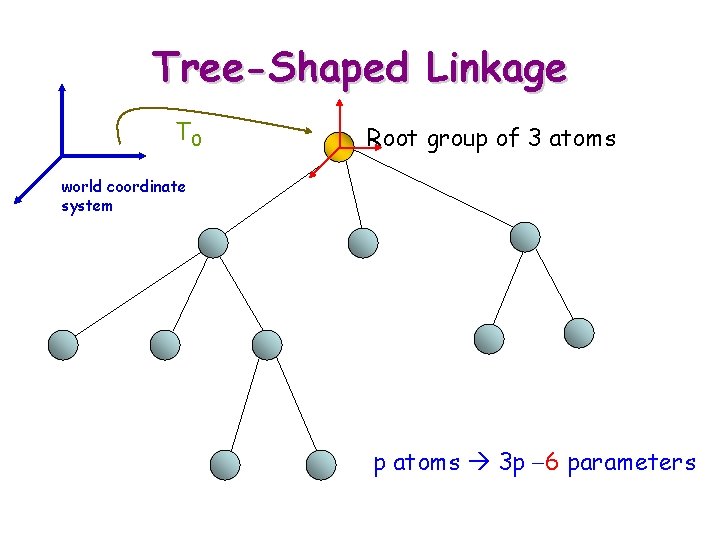
Tree-Shaped Linkage T 0 Root group of 3 atoms world coordinate system p atoms 3 p -6 parameters

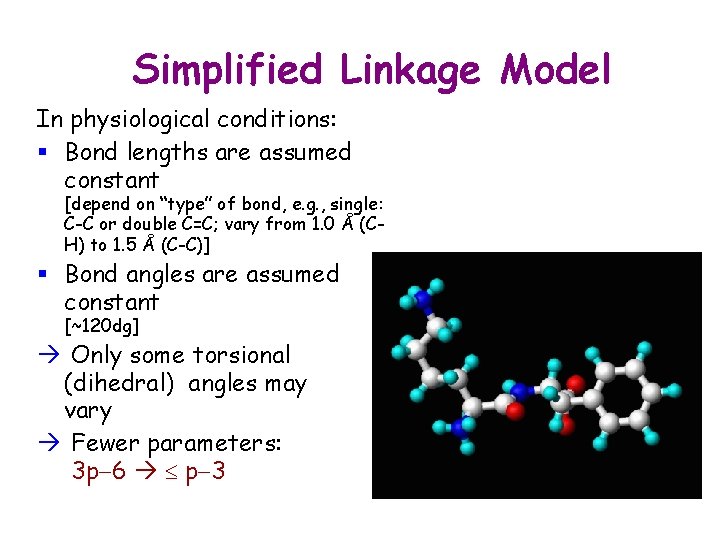
Simplified Linkage Model In physiological conditions: § Bond lengths are assumed constant [depend on “type” of bond, e. g. , single: C-C or double C=C; vary from 1. 0 Å (CH) to 1. 5 Å (C-C)] § Bond angles are assumed constant [~120 dg] Only some torsional (dihedral) angles may vary Fewer parameters: 3 p-6 p-3

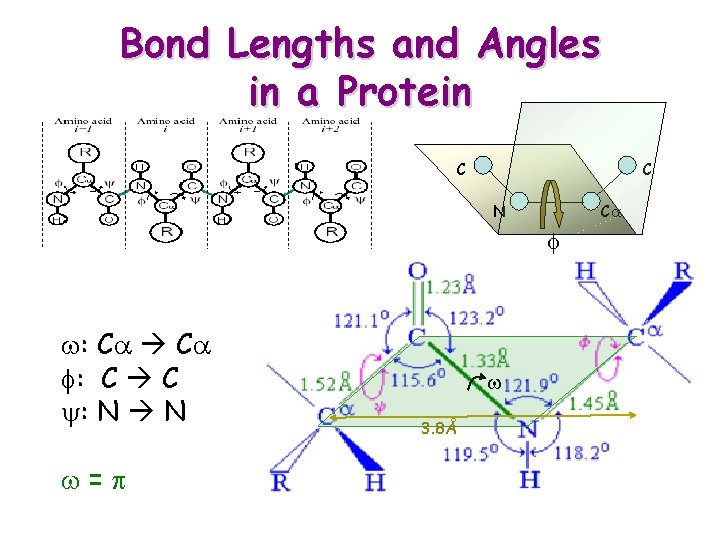
Bond Lengths and Angles in a Protein C C N Ca f w: Ca f: C C y: N N w=p w 3. 8Å

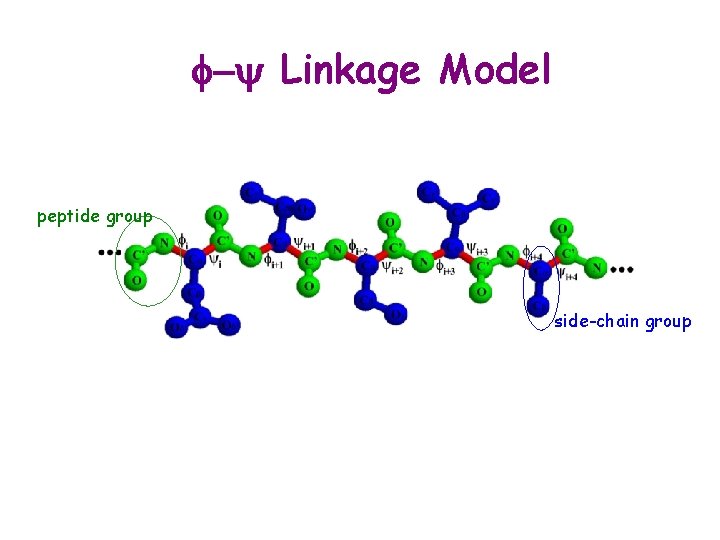
f-y Linkage Model peptide group side-chain group

Convention for f-y Angles § f is defined as the dihedral angle composed of atoms Ci-1–Ni–Cai–Ci § If all atoms are coplanar: C C N Ca f=0 C Ca N C f=p § Sign of f: Use right-hand rule. With right thumb pointing along central bond (N-Ca), a rotation along curled fingers is positive § Same convention for y

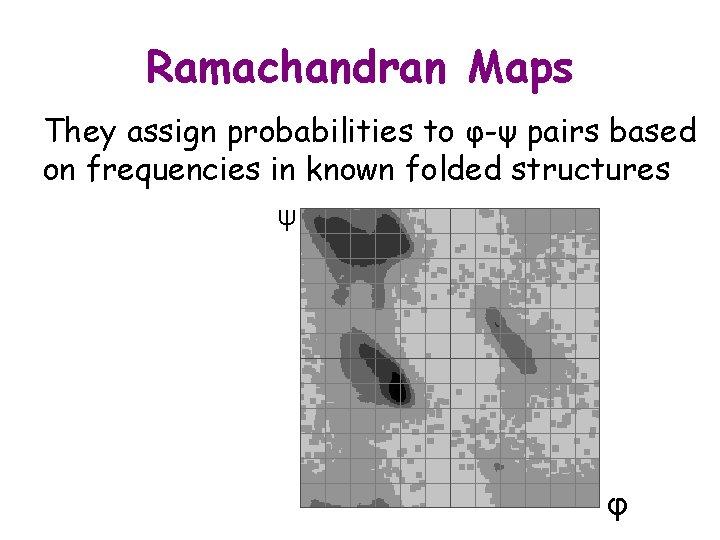
Ramachandran Maps They assign probabilities to φ-ψ pairs based on frequencies in known folded structures ψ φ

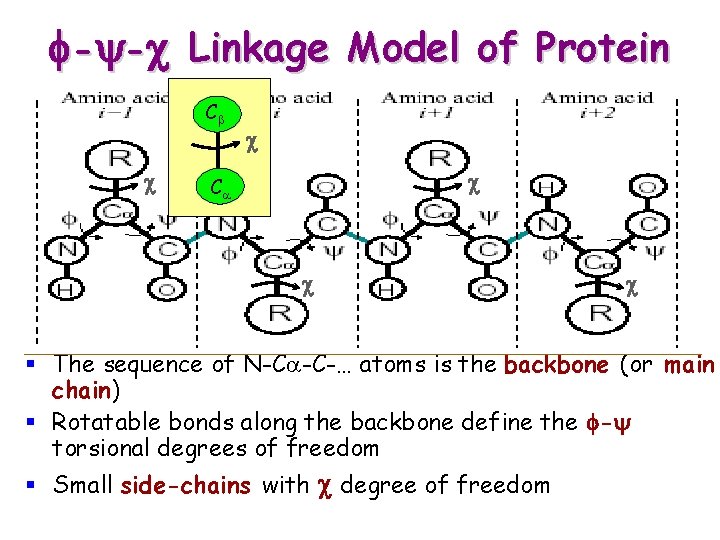
f-y-c Linkage Model of Protein Cb c c c Ca c c § The sequence of N-Ca-C-… atoms is the backbone (or main chain) § Rotatable bonds along the backbone define the f-y torsional degrees of freedom § Small side-chains with c degree of freedom

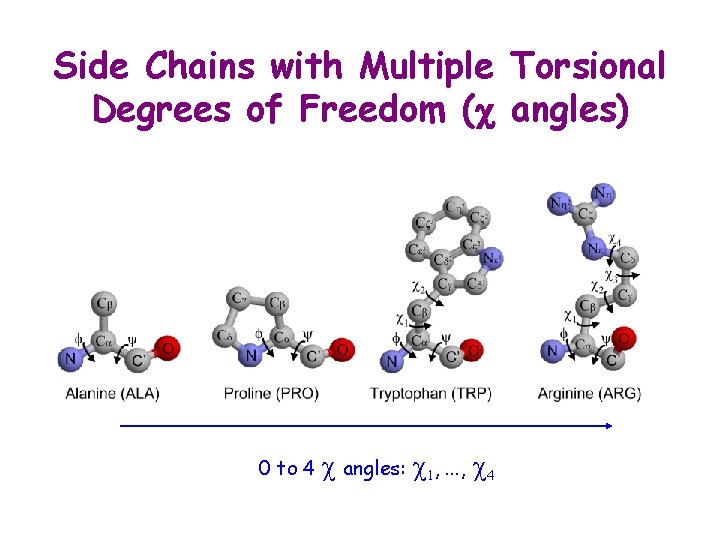
Side Chains with Multiple Torsional Degrees of Freedom (c angles) 0 to 4 c angles: c 1, . . . , c 4

Kinematic Models of Bio-Molecules § Atomistic model: The position of each atom is defined by its coordinates in 3 -D space Drawback: Fixed bond lengths/angles are encoded as additional constraints. More parameters § Linkage model: The kinematics is defined by internal parameters (bond lengths and angles, and torsional angles around bonds) Drawback: Small local changes may have big global effects. Errors accumulate. Forces are more difficult to express § Simplified (f-y-c) linkage model: Fixed bond lengths, bond angles and torsional angles are directly embedded in the representation. Drawback: Fine tuning is difficult

In linkage model a small local change may have big global effect Computational errors may accumulate

Drawback of Homogeneous Coordinate Matrix x’ y’ z’ = 1 i 2 i 3 0 j 1 j 2 j 3 0 k 1 k 2 k 3 0 tx ty tz 1 x y z 1 Too many rotation parameters Accumulation of computing errors along a protein backbone and repeated computation Non-redundant 3 -parameter representations of rotations have many problems: singularities, no simple algebra A useful, less redundant representation of rotation is the unit quaternion

Unit Quaternion R(r, q) = (cos q/2, r 1 sin q/2, r 2 sin q/2, r 3 sin q/2) = cos q/2 + r sin q/2 R(r, q) R(r, q+2 p) Space of unit quaternions: Unit 3 -sphere in 4 -D space with antipodal points identified

Operations on Quaternions P = p 0 + p Q = q 0 + q Product R = r 0 + r = PQ r 0 = p 0 q 0 – p. q (“. ” denotes inner product) r = p 0 q + q 0 p + p q (“ ” denotes outer product) Conjugate of P: P* = p 0 - p

Transformation of a Point x = (x, y, z) quaternion 0 + x Transform of translation t = (tx, ty, tz) and rotation (n, q) Transform of x is x’ 0 + x’ = R(n, q) (0 + x) R*(n, q) + (0 + t)
 2018 geometry bootcamp answers
2018 geometry bootcamp answers Binomial vs geometric variables
Binomial vs geometric variables Modals and semi modals
Modals and semi modals Math supplemental aids
Math supplemental aids Pictorial models of geometric figures
Pictorial models of geometric figures Staar spanish
Staar spanish Types of geometric models
Types of geometric models Camera models in computer vision
Camera models in computer vision Geometric models in machine learning
Geometric models in machine learning Closed kinetic chain exercises
Closed kinetic chain exercises Section 8-1 carbohydrates fats and proteins answer key
Section 8-1 carbohydrates fats and proteins answer key Protein domains and motifs
Protein domains and motifs Organic compounds such as proteins and starches are too
Organic compounds such as proteins and starches are too Lbv protein list
Lbv protein list Section 8-1 summary carbohydrates fats and proteins
Section 8-1 summary carbohydrates fats and proteins Salting in salting out
Salting in salting out Protein definition
Protein definition Dna rna and proteins study guide answers
Dna rna and proteins study guide answers Protein structure
Protein structure What is the connection between genes and proteins
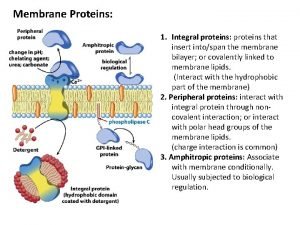
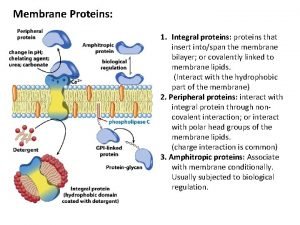
What is the connection between genes and proteins Integral and peripheral proteins
Integral and peripheral proteins Amidomalonate synthesis mechanism
Amidomalonate synthesis mechanism Ribosome factory part or worker
Ribosome factory part or worker Integral and peripheral proteins
Integral and peripheral proteins Difference between affinity and ion exchange chromatography
Difference between affinity and ion exchange chromatography Mitochondrial vesicles
Mitochondrial vesicles Diet chart for diabetic patients
Diet chart for diabetic patients Microfilament function
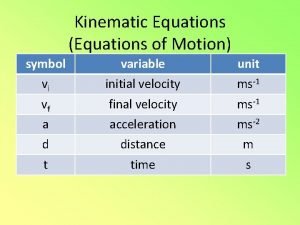
Microfilament function Kinematic equations for uniformly accelerated motion
Kinematic equations for uniformly accelerated motion Timeless kinematic equation
Timeless kinematic equation Timeless kinematic equation
Timeless kinematic equation Big 4 equations
Big 4 equations Rotational kinematics
Rotational kinematics Otto emissions is driving his car at 25.0 m s
Otto emissions is driving his car at 25.0 m s Big four kinematic equations
Big four kinematic equations Pre kinematic texture
Pre kinematic texture Kinematic equatiobs
Kinematic equatiobs Third kinematic equation
Third kinematic equation Kinematic equaitons
Kinematic equaitons Kinematic equations symbols
Kinematic equations symbols Big 5 kinematic equations
Big 5 kinematic equations Kinematic equation
Kinematic equation Fluid mechanics chapter 1
Fluid mechanics chapter 1 Viscosity units
Viscosity units What is vertical velocity
What is vertical velocity Track manager
Track manager Kinematic mount design
Kinematic mount design Xf = xi + vt
Xf = xi + vt Kinematic equations derivation
Kinematic equations derivation Si unit of angular acceleration
Si unit of angular acceleration Tools for measuring kinematic quantities
Tools for measuring kinematic quantities Shear press kinematic diagram
Shear press kinematic diagram Basic kinematic equation bke
Basic kinematic equation bke Kinematics of rigid bodies
Kinematics of rigid bodies Kinematic equation for instantaneous velocity
Kinematic equation for instantaneous velocity Kinematic equations for circular motion
Kinematic equations for circular motion Kinematic motion along a straight line
Kinematic motion along a straight line Suvat equations a level
Suvat equations a level Real time kinematic
Real time kinematic Kinematic
Kinematic Hydraulic cylinder kinematic diagram
Hydraulic cylinder kinematic diagram Trajectory equation of projectile
Trajectory equation of projectile Kinematic
Kinematic Toppling failure stereonet
Toppling failure stereonet Channel vs carrier proteins
Channel vs carrier proteins Globular vs fibrous proteins
Globular vs fibrous proteins All enzymes are globular proteins
All enzymes are globular proteins Proteins the body's building blocks worksheet answers
Proteins the body's building blocks worksheet answers Example of denatured protein
Example of denatured protein What are derived proteins
What are derived proteins Monomers protein
Monomers protein Protein digestion
Protein digestion How do proteins fold
How do proteins fold Protien database
Protien database