Kinematic Equations Kinematic Equations Recall 1 dimensional kinematic

Kinematic Equations

Kinematic Equations • Recall: 1 dimensional kinematic equations for uniform (constant) acceleration (Ch. 2). • We’ve jseen analogies between linear & angular quantities: Displacement & Angular Displacement: x θ Velocity & Angular Velocity: v ω Acceleration & Angular Acceleration: a α • For α = constant, we can use the same kinematic equations from Ch. 2 with these replacements!

The equations of motion for constant angular acceleration are the same as those for linear motion, substituting the angular quantities for the linear ones. For α = constant, & using the replacements x θ, v ω, a α we get the equations: NOTE These are ONLY VALID if all angular quantities are in radian units!!

Example: Centrifuge Acceleration A centrifuge rotor is accelerated from rest to frequency f = 20, 000 rpm in 30 s. a. Calculate its average angular acceleration. b. Through how many revolutions has the centrifuge rotor turned during its acceleration period, assuming constant angular acceleration?

Example: Rotating Wheel • A wheel rotates with constant angular acceleration α = 3. 5 rad/s 2. It’s angular speed at time t = 0 is ω0 = 2. 0 rad/s. (A) Calculate the angular displacement Δθ it makes after t = 2 s. Use: Δθ = ω0 t + (½)αt 2 = (2)(2) + (½)(3)(2)2 = 11. 0 rad (630º) (B) Calculate the number of revolutions it makes in this time. Convert Δθ from radians to revolutions: A full circle = 360º = 2π radians = 1 revolution 11. 0 rad = 630º = 1. 75 rev (C) Find the angular speed ω after t = 2 s. Use: ω = ω0 + αt = 2 + (3. 5)(2) = 9 rad/s

Example: CD Player • Consider a CD player playing a CD. For the player to read a CD, the angular speed ω must vary to keep the (v = ωr). A CD has inner radius ri = 23 mm = 2. 3 10 -2 m & outer radius ro = 58 mm = 5. 8 10 -2 m. The tangential speed at the outer radius is v = 1. 3 m/s. (A) Find angular speed in rev/min at the inner & outer radii: ωi = (v/ri) = (1. 3)/(2. 3 10 -2) = 57 rad/s = 5. 4 102 rev/min ωo = (v/ro) = (1. 3)/(5. 8 10 -2) = 22 rad/s = 2. 1 102 rev/min tangential speed constant • (B) Standard playing time for a CD is 74 min, 33 s (= 4, 473 s). How many revolutions does the disk make in that time? θ = (½)(ωi + ωf)t = (½)(57 + 22)(4, 473 s) = 1. 8 105 radians = 2. 8 104 revolutions

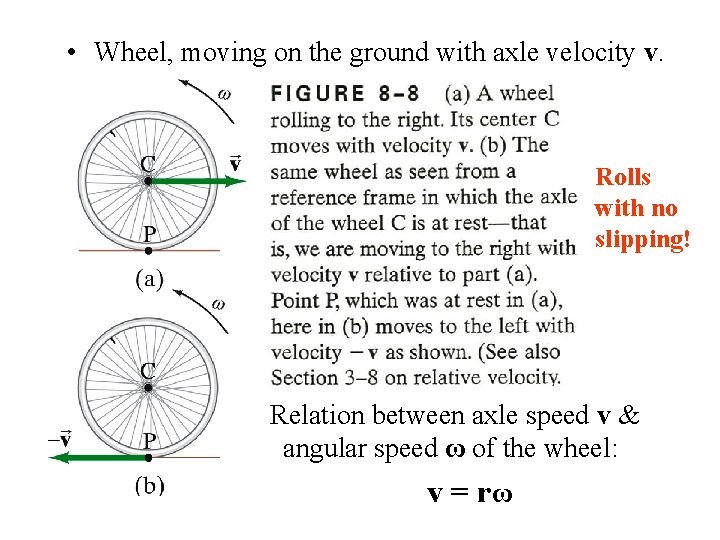
Rolling Motion • Without friction, there would be no rolling motion. • Assume: Rolling motion with no slipping Can use static friction • Rolling (of a wheel) involves: – Rotation about the Center of Mass (CM) PLUS – Translation of the CM

• Wheel, moving on the ground with axle velocity v. Rolls with no slipping! ω Relation between axle speed v & angular speed ω of the wheel: v = rω

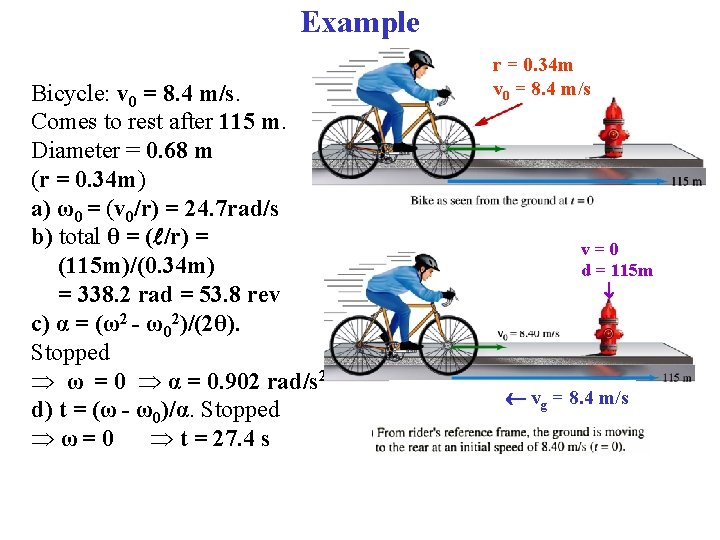
Example Bicycle: v 0 = 8. 4 m/s. Comes to rest after 115 m. Diameter = 0. 68 m (r = 0. 34 m) a) ω0 = (v 0/r) = 24. 7 rad/s b) total θ = ( /r) = (115 m)/(0. 34 m) = 338. 2 rad = 53. 8 rev c) α = (ω2 - ω02)/(2θ). Stopped ω = 0 α = 0. 902 rad/s 2 d) t = (ω - ω0)/α. Stopped ω= 0 t = 27. 4 s r = 0. 34 m v 0 = 8. 4 m/s v=0 d = 115 m vg = 8. 4 m/s