Funo quadrtica a funo geral de 1 grau

Função quadrática: a função geral de 1º grau RANILDO LOPES 1

Função quadrática: a função geral de 1º grau A temperatura de uma substância é 30 ºC. Vamos analisar duas situações distintas. 2

① Sua temperatura varia com o tempo de maneira uniforme, aumentando 10 ºC por minuto. Veja as temperaturas da substância, medidas minuto a minuto. t(min) 0 1 2 3 4 5 T(o. C) 30 40 50 60 70 80 A taxa de variação da temperatura é positiva (10 o. C/min). Após t minutos, a temperatura T da substância em o. C é, T = 30 + 10. t 3

② Sua temperatura varia com o tempo de maneira uniforme, diminuindo 10 ºC por minuto. Veja as temperaturas da substância, medidas minuto a minuto. t(min) 0 1 2 3 4 5 T(o. C) 30 20 10 0 – 10 – 20 A taxa de variação da temperatura é negativa (10 o. C/min). Após t minutos, a temperatura T da substância em o. C é, T = 30 – 10. t 4

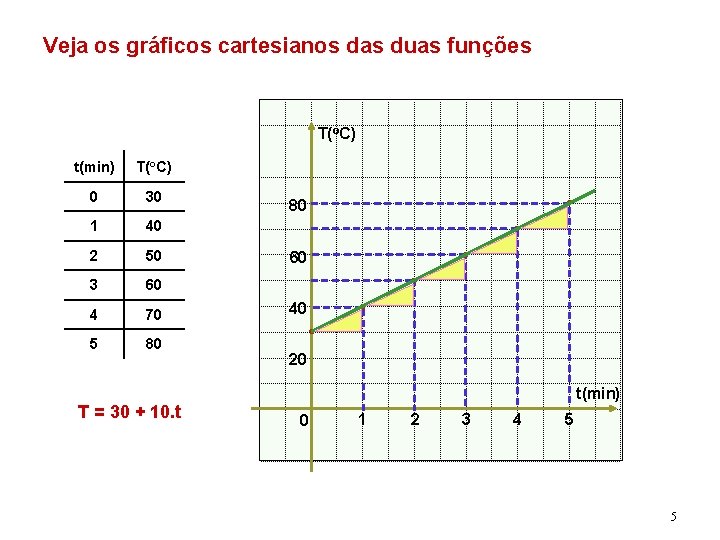
Veja os gráficos cartesianos das duas funções T(o. C) t(min) T(o. C) 0 30 1 40 2 50 3 60 4 70 5 80 T = 30 + 10. t 80 60 40 20 t(min) 0 1 2 3 4 5 5

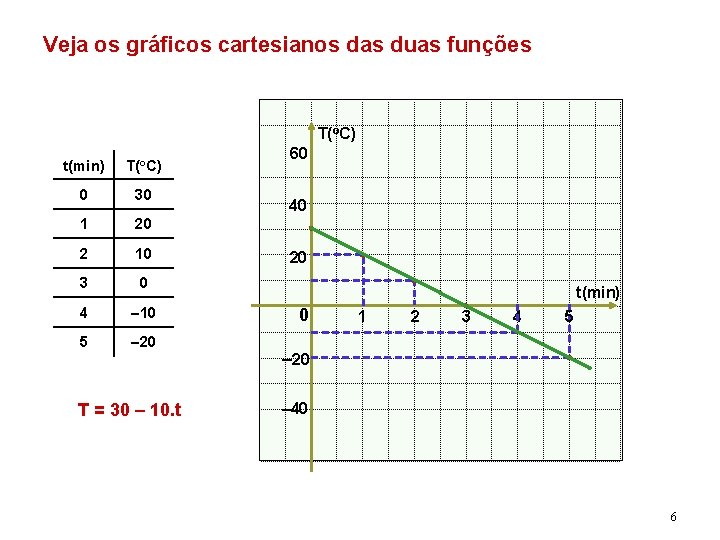
Veja os gráficos cartesianos das duas funções T(o. C) t(min) T(o. C) 0 30 1 20 2 10 3 0 4 – 10 5 – 20 T = 30 – 10. t 60 40 20 t(min) 0 1 2 3 4 5 – 20 – 40 6

Função afim ou de 1º grau é toda função do tipo y = f(x) = ax + b Em que a e b são constantes reais, com a ≠ 0. Se b = 0, temos a função y = f(x) = ax, chamada, também, função linear. 7

Exemplos q y = f(x) = 5 x – 3 é uma função afim com a = 5 e b = – 3. q y = f(x) = – 2 x é uma função afim, com a = – 2 e b = 0 Nesse caso a função é chamada de linear. 8

Características da função afim y = f(x) = ax + b. n A fórmula que a define é um polinômio de 1º grau; seu termo independente pode ser nulo ou não. n Se b = 0, temos a função f(x) = ax, chamada de função linear. n A constante real a, não-nula, é o coeficiente angular. Ela é a mesma, qualquer que seja o intervalo considerado. 9

Características da função afim y = f(x) = ax + b. n A constante real b é o coeficiente linear. n Seu gráfico cartesiano é uma linha reta, não paralela aos eixos. Ela pode conter a origem (caso b = 0) ou não conter origem (caso b ≠ 0). n O crescimento ou o decrescimento da função estão relacionados com o sinal de a. A reta é ascendente para a > 0 e descendente para a < 0. 10

Crescimento e decrescimento. a>0 ⇒ função crescente ⇒ reta ascendente (sobe da esquerda p/ direita) a<0 ⇒ função decrescente ⇒ reta descendente (desce da esquerda p/ direita) 11

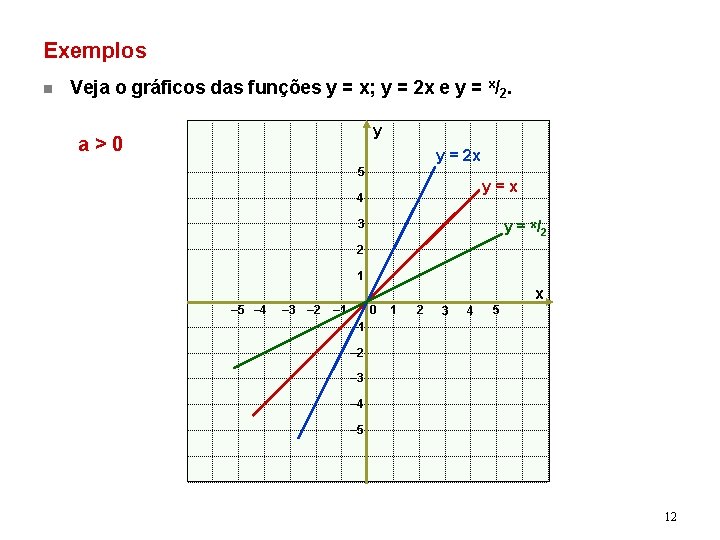
Exemplos n Veja o gráficos das funções y = x; y = 2 x e y = x/2. y a>0 y = 2 x 5 y=x 4 3 y = x/ 2 2 1 x – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 – 1 – 2 – 3 – 4 – 5 12

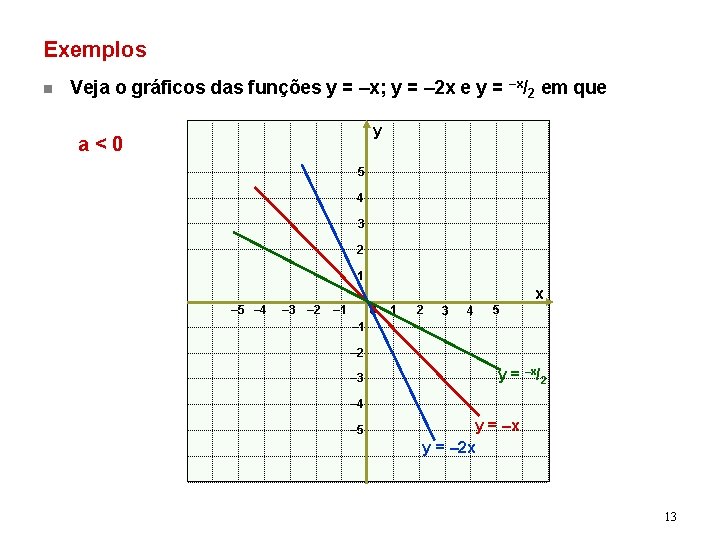
Exemplos n Veja o gráficos das funções y = –x; y = – 2 x e y = –x/ 2 em que y a<0 5 4 3 2 1 x – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 – 1 – 2 – 3 y = –x/2 – 4 – 5 y = –x y = – 2 x 13

A partir do gráfico da função linear y = ax, podemos obter os gráficos de todas as funções afins y = ax + b. Deslocamos o gráfico da função y = ax para cima ou para baixo, de acordo com o valor da constante b. 14

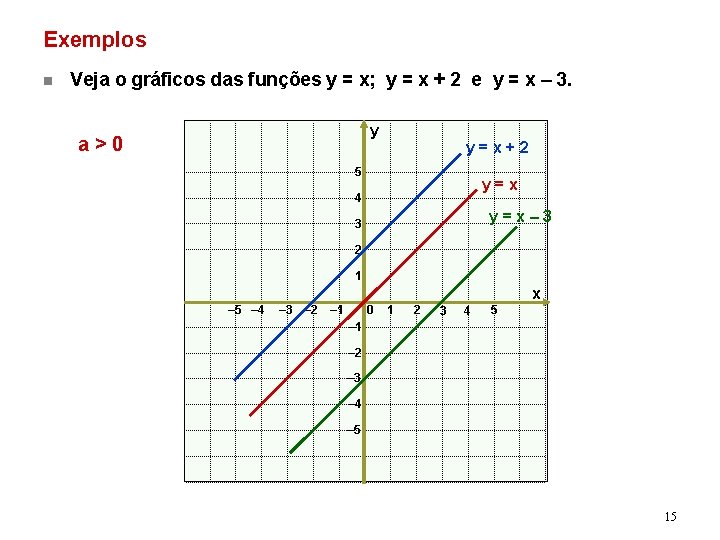
Exemplos n Veja o gráficos das funções y = x; y = x + 2 e y = x – 3. y a>0 y=x+2 5 y=x 4 y=x– 3 3 2 1 x – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 – 1 – 2 – 3 – 4 – 5 15

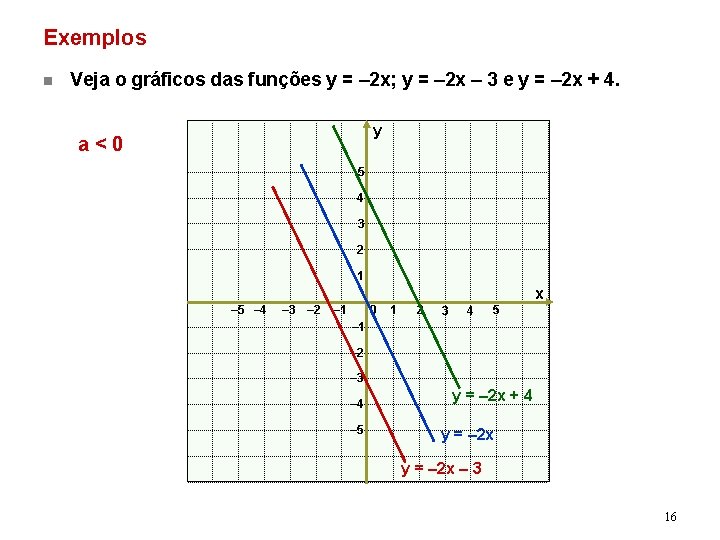
Exemplos n Veja o gráficos das funções y = – 2 x; y = – 2 x – 3 e y = – 2 x + 4. y a<0 5 4 3 2 1 x – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 – 1 – 2 – 3 – 4 – 5 y = – 2 x + 4 y = – 2 x – 3 16

A análise das duas últimas figuras nos sugere um caso geral em relação a todas as funções afins do tipo y = f(x) = ax + b. n Que relação existe entre o coeficiente b e o ponto onde cada reta corta o eixo y? b é a ordenada do ponto em que a reta corta o eixo y. Ou seja, a reta intercepta o eixo y no ponto de coordenadas (0, b). 17

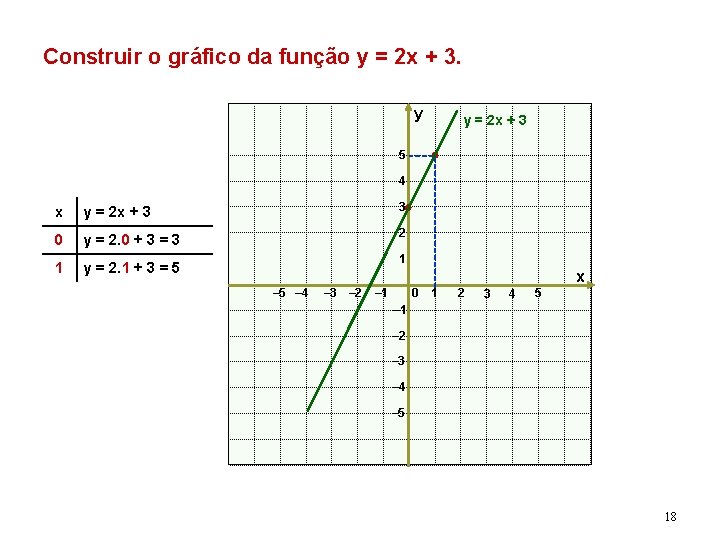
Construir o gráfico da função y = 2 x + 3. y y = 2 x + 3 5 4 x y = 2 x + 3 3 0 y = 2. 0 + 3 = 3 2 1 y = 2. 1 + 3 = 5 1 x – 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5 – 1 – 2 – 3 – 4 – 5 18

Dois pontos determinam uma reta. Por isso, se conhecermos dois de seus pontos, podemos obter a função afim que ela representa. Ou seja, podemos obter os coeficientes a e b da função. 20

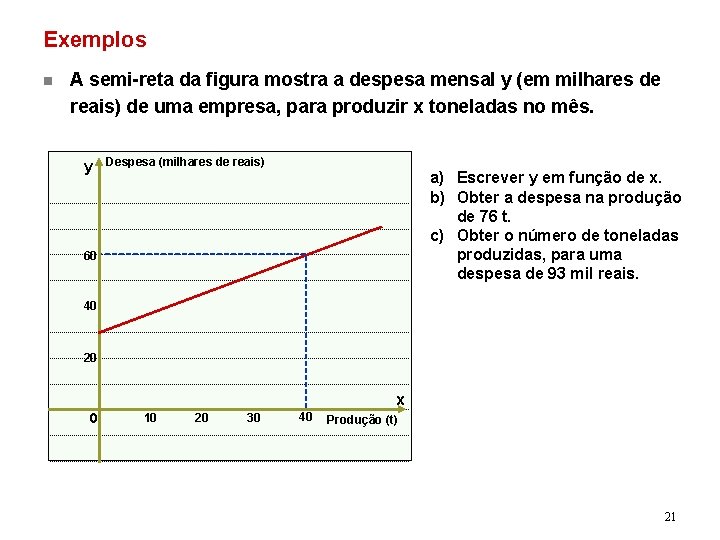
Exemplos n A semi-reta da figura mostra a despesa mensal y (em milhares de reais) de uma empresa, para produzir x toneladas no mês. y Despesa (milhares de reais) a) Escrever y em função de x. b) Obter a despesa na produção de 76 t. c) Obter o número de toneladas produzidas, para uma despesa de 93 mil reais. 60 40 20 x 0 10 20 30 40 Produção (t) 21

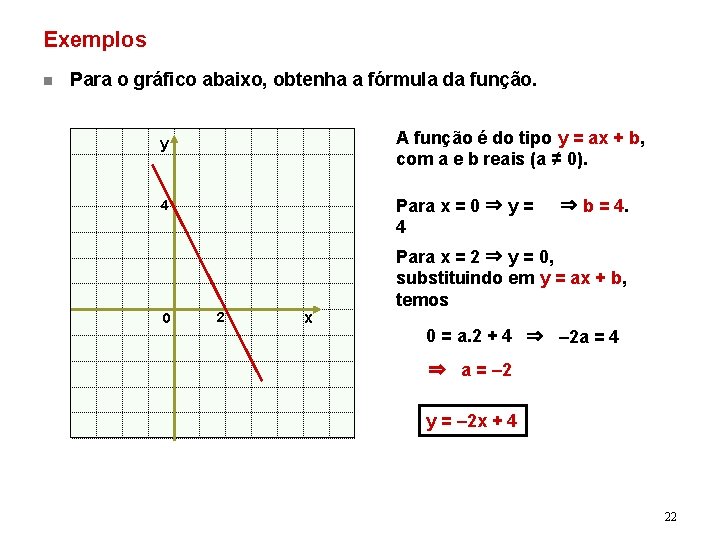
Exemplos n Para o gráfico abaixo, obtenha a fórmula da função. A função é do tipo y = ax + b, com a e b reais (a ≠ 0). y Para x = 0 ⇒ y = 4 4 0 2 x ⇒ b = 4. Para x = 2 ⇒ y = 0, substituindo em y = ax + b, temos 0 = a. 2 + 4 ⇒ – 2 a = 4 ⇒ a = – 2 y = – 2 x + 4 22

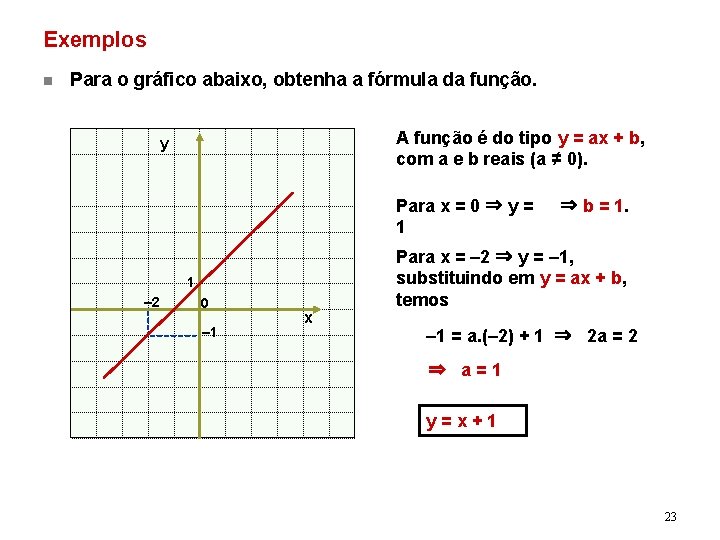
Exemplos n Para o gráfico abaixo, obtenha a fórmula da função. A função é do tipo y = ax + b, com a e b reais (a ≠ 0). y Para x = 0 ⇒ y = 1 1 – 2 0 – 1 x ⇒ b = 1. Para x = – 2 ⇒ y = – 1, substituindo em y = ax + b, temos – 1 = a. (– 2) + 1 ⇒ 2 a = 2 ⇒ a=1 y=x+1 23