Funo Linear e Funo Quadrtica Professora Ursula Timm

Função Linear e Função Quadrática Professora Ursula Timm

Função Linear Uma função linear é uma função da forma y = f(x) = ax+b, onde a é chamado de coeficiente angular e indica a inclinação, ou a taxa de variação de y em relação a x. O valor de b é chamado de coeficiente linear e indica onde o eixo y é interceptado, ou seja, quando x é zero. O gráfico da função linear é uma reta.

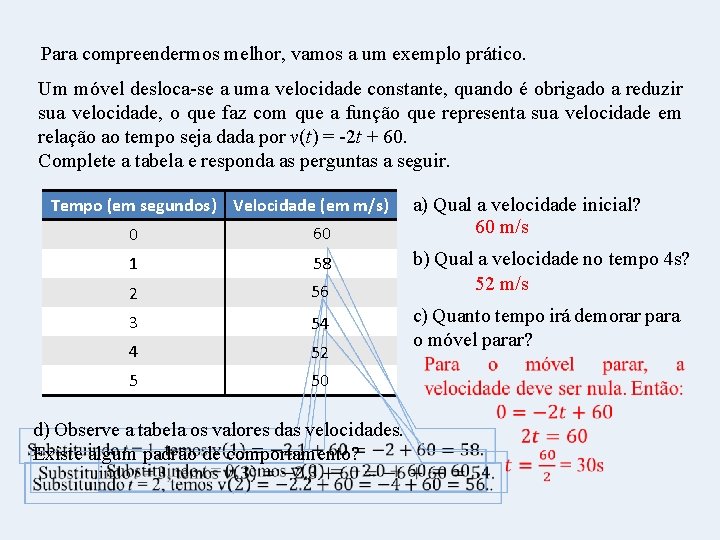
Para compreendermos melhor, vamos a um exemplo prático. Um móvel desloca-se a uma velocidade constante, quando é obrigado a reduzir sua velocidade, o que faz com que a função que representa sua velocidade em relação ao tempo seja dada por v(t) = -2 t + 60. Complete a tabela e responda as perguntas a seguir. Tempo (em segundos) Velocidade (em m/s) 0 60 1 58 2 56 3 54 4 52 5 50 d) Observe a tabela os valores das velocidades. Existe algum padrão de comportamento? a) Qual a velocidade inicial? 60 m/s b) Qual a velocidade no tempo 4 s? 52 m/s c) Quanto tempo irá demorar para o móvel parar?

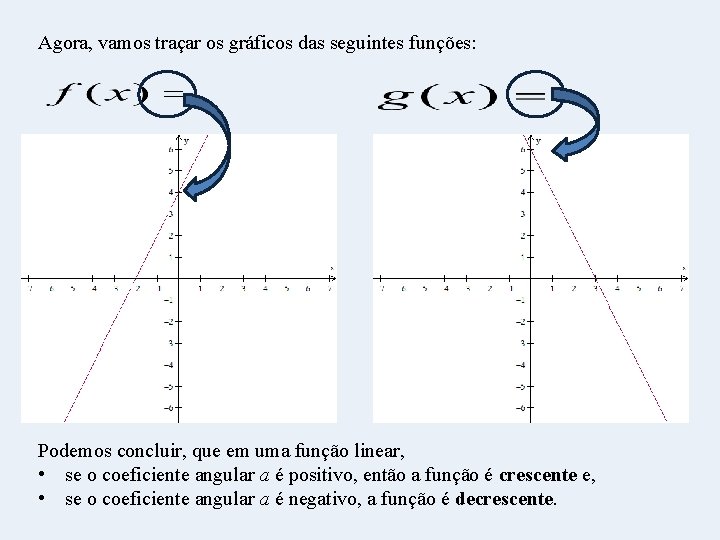
Agora, vamos traçar os gráficos das seguintes funções: Podemos concluir, que em uma função linear, • se o coeficiente angular a é positivo, então a função é crescente e, • se o coeficiente angular a é negativo, a função é decrescente.

RESUMO GRÁFICO

Função Quadrática

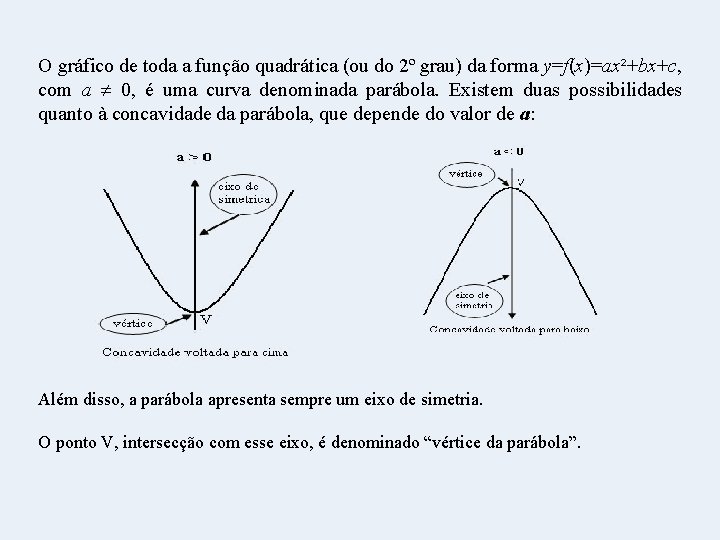
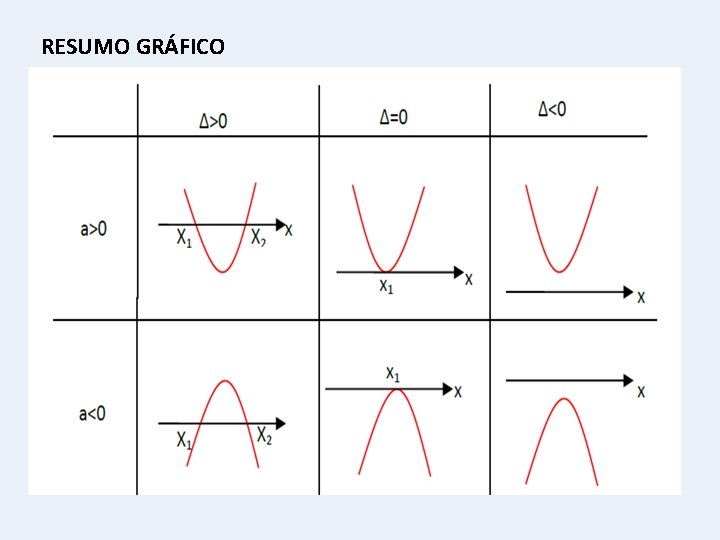
O gráfico de toda a função quadrática (ou do 2º grau) da forma y=f(x)=ax²+bx+c, com a 0, é uma curva denominada parábola. Existem duas possibilidades quanto à concavidade da parábola, que depende do valor de a: Além disso, a parábola apresenta sempre um eixo de simetria. O ponto V, intersecção com esse eixo, é denominado “vértice da parábola”.

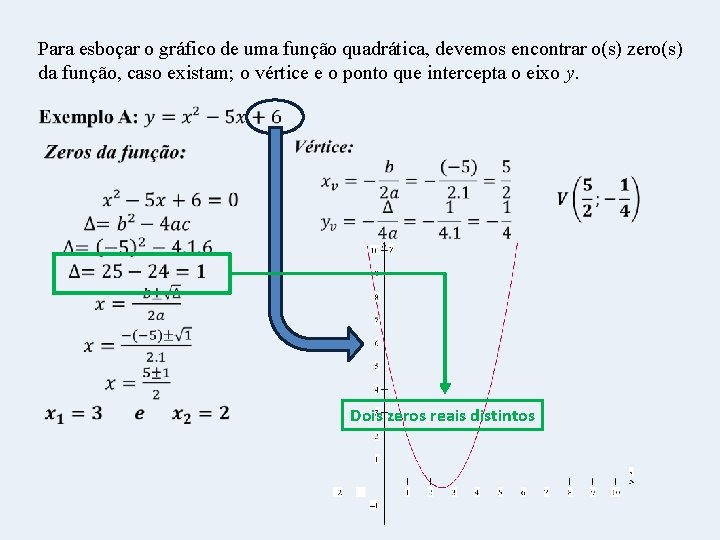
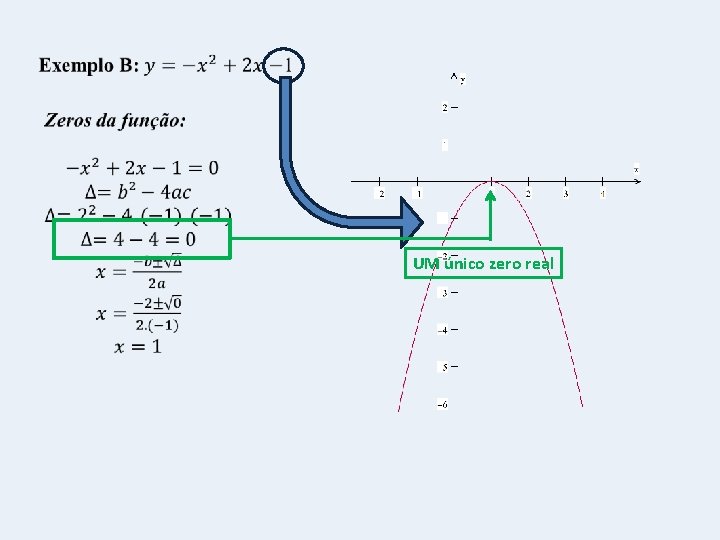
Para esboçar o gráfico de uma função quadrática, devemos encontrar o(s) zero(s) da função, caso existam; o vértice e o ponto que intercepta o eixo y. Dois zeros reais distintos

UM único zero real

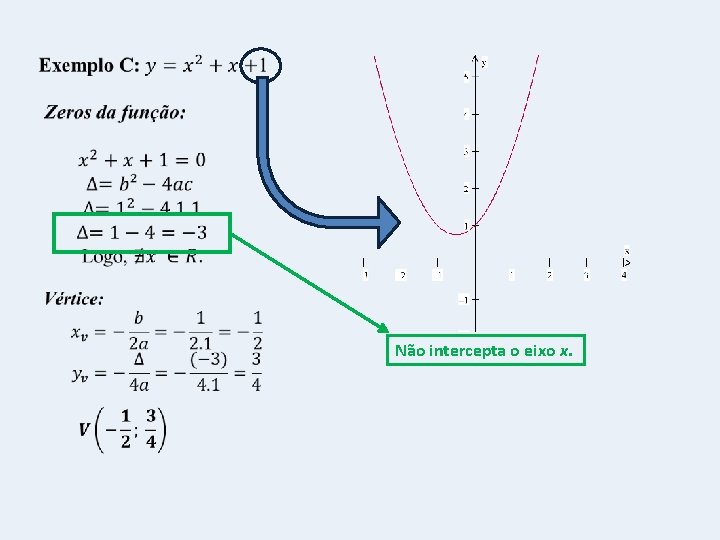
Não intercepta o eixo x.

RESUMO GRÁFICO

Máximo e Imagem § Im(f) = {y ∈ ℝly ≤ 3} § f tem um máximo em (2, 3). Logo, ym = 3 é o valor máximo de f(x).

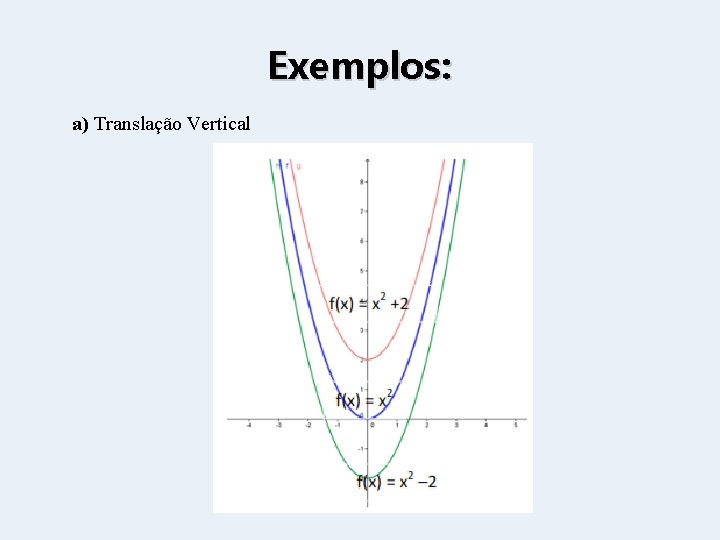
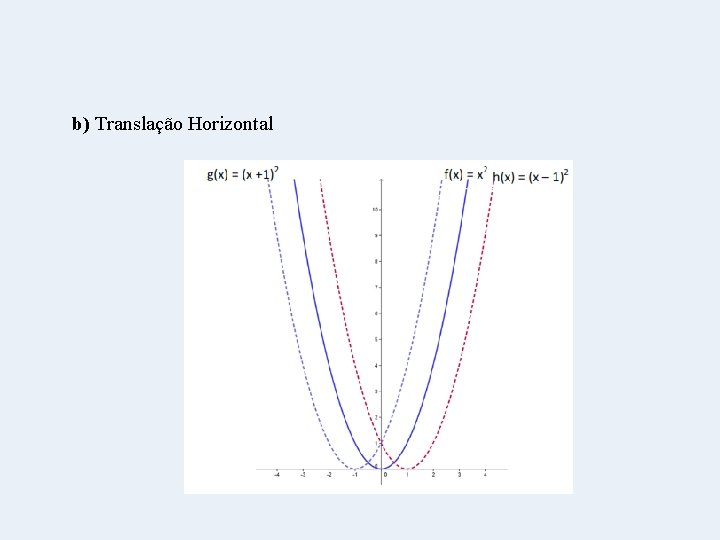
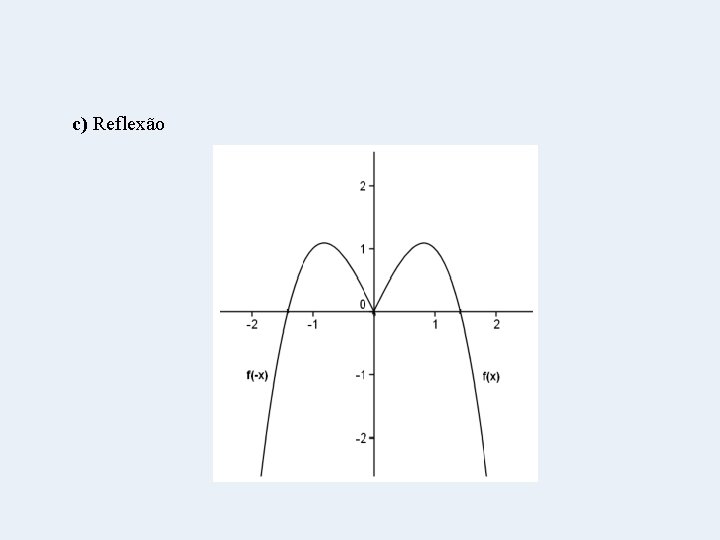
Translação e Reflexão • Translação é a transformação em que todos os pontos de uma figura se deslocam numa mesma direção, sentido e de uma mesma distância. • Quando somamos um número a uma função estamos fazendo uma translação vertical, isto é, o gráfico desloca-se no sentido vertical uma quantidade de vezes equivalente ao número somado (ou subtraído). • Quando somamos ou subtraímos um número ao argumento da função, deslocamos o gráfico para a direita ou esquerda (horizontal) uma quantidade equivalente ao número somado ou subtraído, porém no sentido contrário à operação. Esta é uma translação horizontal. • Quando multiplicamos o gráfico por 1 estamos fazendo uma reflexão, em relação ao eixo x. • Obs. : Estes são apenas alguns tipos de translações e reflexões. Porém, estas ideias não se aplicam apenas à função quadrática, mas sim a qualquer tipo de função!

Exemplos: a) Translação Vertical

b) Translação Horizontal

c) Reflexão

A invenção do basquete Um esporte que pudesse ser praticado por várias pessoas, fácil de aprender, que pudesse ser adaptado a um espaço fechado e não fosse violento. Esse foi o pedido que o diretor da faculdade Springfield, de Massachussetts, fez ao professor James Naismith. No rigoroso inverno de 1892, era necessário inventar alguma atividade esportiva que motivasse os alunos, impossibilitados de praticar esportes ao ar livre e entediados com as aulas de ginástica. Naismith meditou na encomenda do diretor: para um jogo coletivo pensou logo na bola. Mas não queria que ela fosse chutada ou ficasse muito tempo retida nas mãos dos jogadores. Para acertar o alvo, eles deveriam lançar a bola descrevendo uma parábola, o que evitaria a violência do arremesso na horizontal. Essas seriam as regras básicas. Com o zelador da faculdade, Naismith conseguiu dois velhos cestos para colheita de pêssego e pendurou-os a 3, 05 m de altura em duas pilastras nas extremidades do ginásio. Surgia, assim, a cesta do jogo, e, com ela, o próprio nome do esporte: basketball, basquete ou bola ao cesto. As primeiras cestas (cestos) tinham o fundo fechado. A cada arremesso um jogador tinha que subir numa escada para resgatar a bola. Depois alguém teve a ideia de cortar o fundo do cesto e, assim, agilizar a partida.

Questões de aprendizagem

6) Dada a função y = 2 x – 6, determine: a) o ponto onde o gráfico intercepta o eixo y; b) a raiz da função (o ponto de intersecção com o eixo x); c) o gráfico da função; d) o sinal da função; e) a função é crescente ou decrescente. 7) Dada a função y = 3 x – 2, determine: a) o ponto onde o gráfico intercepta o eixo y; b) a raiz da função (o ponto de intersecção com o eixo x); c) o gráfico da função; d) o sinal da função; e) a função é crescente ou decrescente. 8) Dada a função y = x, trace o seu gráfico e, em seguida, utilizando a ideia de translação e reflexão, trace o gráfico das funções abaixo. a) y = x + 3 b) y = x – 4 c) y = – x d) y = – x + 1 e) y = – x – 2

Funções no cotidiano. . . Tarifa. Em certa cidade, a tarifa de táxi é calculada da seguinte forma: R$ 5, 00 a bandeirada mais R$ 1, 20 por quilômetro rodado. a) Pode-se estabelecer uma função entre essas grandezas? Em caso positivo, quais seriam as variáveis (dependente e independente) dessa função? b) Qual lei matemática definiria essa função?

Distância. Com o auxílio de um cronômetro, marcando-se o tempo em hora, verificaram-se as distâncias percorridas por um móvel. Essas distâncias, percorridas em determinados Tempo (h) 0, 2 0, 4 0, 8 1, 6 2 x Distância 10 20 80 100 50 x 40 (km) Queremos agora calcular x para f(x) = 330. DENNIS MACDONALD/AGE/ GRUPO KEYSTONE tempos, foram registradas na tabela a seguir: Substituindo o valor de f(x) na lei da função, temos: a) Indicarcalcular as variáveis e indicamos independente) Queremos f(x) para(dependente x = 2, 8, o que por relacionadas 330 = 50 xnessa x situação. = 6, 6. f(2, 8). Substituindo o valor de x na lei da função, temos: b)Logo, Expressar a lei matemática que relaciona a distância para percorrer 330 quilômetros, o móvel gastou Assumindo que a distância percorrida varia em função do f(2, 8) = 50 f(2, 8) = 140. percorrida ao∙ 2, 8 tempo. 6, 6 horas. tempo, a ou variável (y) é aé distância c) Calcular a f(x) distância quando o tempo igual a 2, 8 eh. a variável y= 50 x =dependente 50 x. d) Calcular o tempo a distância é 330 km. independente (x) équando o tempo.

Navegação. Durante uma situação de emergência, o capitão de um barco dispara um sinalizador para avisar a guarda costeira. A trajetória que o sinal luminoso descreve é um arco de parábola. A função que descreve o movimento do sinal luminoso é dada por: h(t) = 80 t – 5 t 2, sendo h a altura do sinal, em metro, e t o tempo decorrido após o disparo, em segundo. a) Qual é a altura máxima que esse sinal luminoso pode atingir? b) Quantos segundos se passam, após o disparo, até o sinal luminoso atingir a altura máxima?