Flujos de Carga Load Flow Flujos de carga

Flujos de Carga (Load Flow)

Flujos de carga. v v Se trata de obtener los valores de tensión, potencias activa y reactiva en cada barra de un sistema, conocida la red de transmisión, las relaciones no lineales tensión-corriente en cada barra y las condiciones de carga y generación. Usos: § § § § Diseño (planificación) Operación Cálculo de fallas (cortocircuitos) Estabilidad Pérdidas Despacho Etc. . .

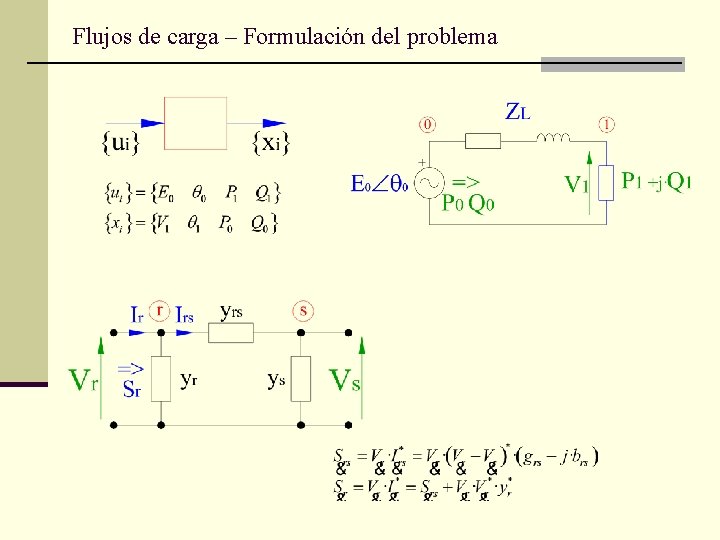
Flujos de carga – Formulación del problema Tipos de barras: PQ, PV, una barra libre. Descripción de la red: (¡Referencias!) Relación de potencia: Tipo Barra P Q E Carga Tensión Controlada Generador Q-<Q<Q+ Cond. Sincrónico 0 Q-<Q<Q+ “PQ” “PV” Impedancia Referencia Comentario Se conoce Z Libre (slack bus)

Flujos de carga – Formulación del problema Soluciones. § Analizador de redes § Gauss-Seidel Newton-Rapson Flujo en continua § § Computador digital Referencias: Ward, Hale “Digital Computer Solution of Power Flow Problem” AIEE Vol 75 pp 398 - 404 1956.

Flujos de carga – Formulación del problema

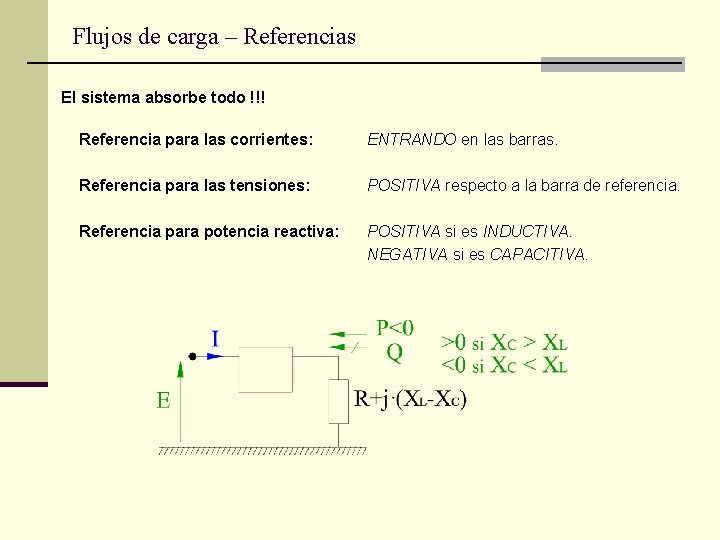
Flujos de carga – Referencias El sistema absorbe todo !!! Referencia para las corrientes: ENTRANDO en las barras. Referencia para las tensiones: POSITIVA respecto a la barra de referencia. Referencia para potencia reactiva: POSITIVA si es INDUCTIVA. NEGATIVA si es CAPACITIVA.

Flujos de carga – Gauss Seidel Algoritmo básico (para barra PQ): Para una barra PV, es necesario “estimar” el valor de Q: Luego de aplicar el algoritmo básico, se corrige para mantener el valor dado.

Flujos de carga – Gauss Seidel Diagrama de cálculo

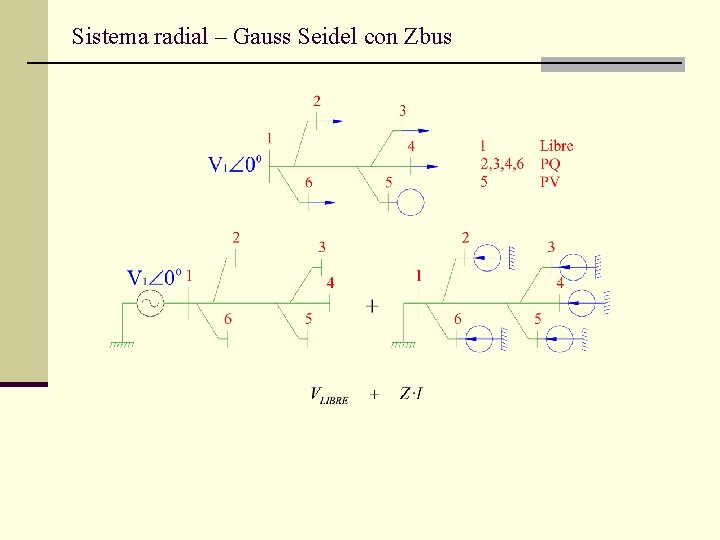
Sistema radial – Gauss Seidel con Zbus

Sistema radial – Gauss Seidel con Zbus Diagrama de cálculo Obs. : Para E 1 conocido (barra 1 es barra libre)

Soluciones tipo Gauss (Jacobi) Ecuaciones: Gauss Seidel:

Comentarios sobre la convergencia de Gauss Seidel Usando: Sea con A = el proceso de solución se puede expresar como:

Comentarios sobre la convergencia de Gauss Seidel álgebra: valor característico vector característico para Si i y xi (i=1. . . n), son los valores y vectores característicos de entonces xi son linealmente independientes y , Ahora para k , si | i|<1(i=1. . . n) el valor de Mk+1·x(0) converge, en caso contrario diverge. En estas condiciones xk+1 x* LA CONVERGENCIA DEPENDE DEL VALOR MÁXIMO DE | i|

Comentarios sobre la convergencia de Gauss Seidel Se puede mejorar la convergencia reduciendo el valor máximo de | i| >1: Factor de aceleración. <1: Factor de desaceleración.

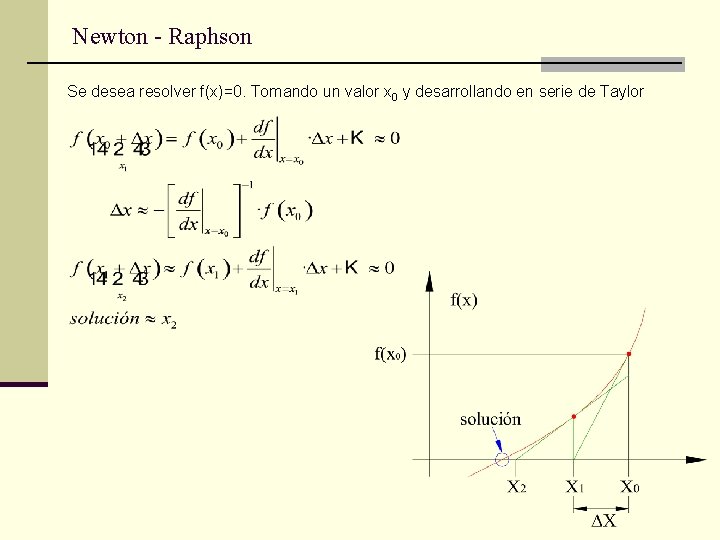
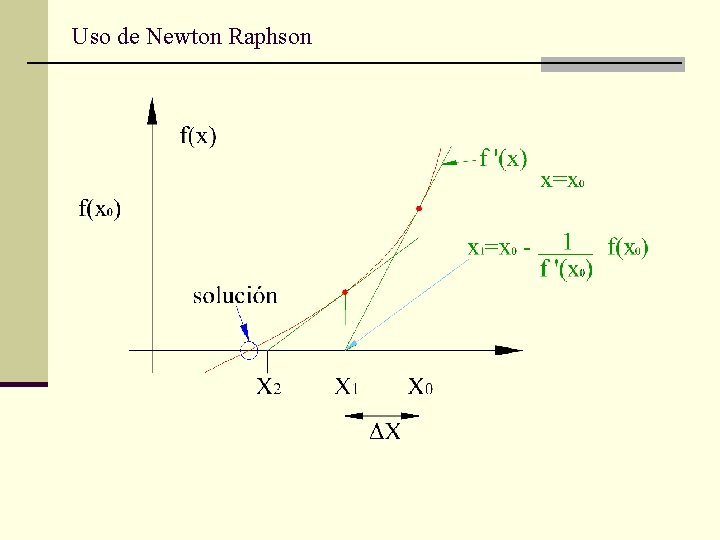
Newton - Raphson Se desea resolver f(x)=0. Tomando un valor x 0 y desarrollando en serie de Taylor

Newton – Raphson (caso varias variables) Serie de Taylor: donde J(X 0) es el Jacobiano de F(X) evaluado en Reordenando:

Newton – Raphson (caso varias variables) Utilizando: Se tiene para un SEP

Newton – Raphson (caso varias variables) La función Nodos PQ: Nodos PV: Donde se observa que: se logra:

Newton – Raphson (Forma cartesiana) Utilizando: Se tiene para un SEP

Newton – Raphson (Forma cartesiana) Elementos del Jacobiano: p q p=q

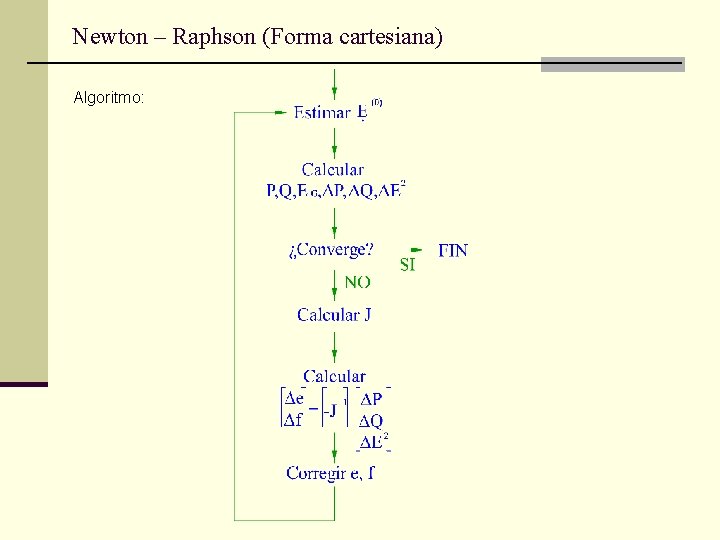
Newton – Raphson (Forma cartesiana) Algoritmo:

Newton – Raphson (Forma polar) Utilizando:

Newton – Raphson (Forma polar) Elementos del Jacobiano: r s r=s

Observaciones sobre Newton – Raphson 1. Mayor requerimiento de memoria, operaciones más complejas que Gauss-Seidel 2. Forma desacoplada al usar expresión polar para V. Ecns. desacopladas para V, 3. Suponiendo: resulta Elementos en derivación excluidos: Que son de la forma I=Y·E, conocido como FLUJO DE CARGA EN CONTINUA

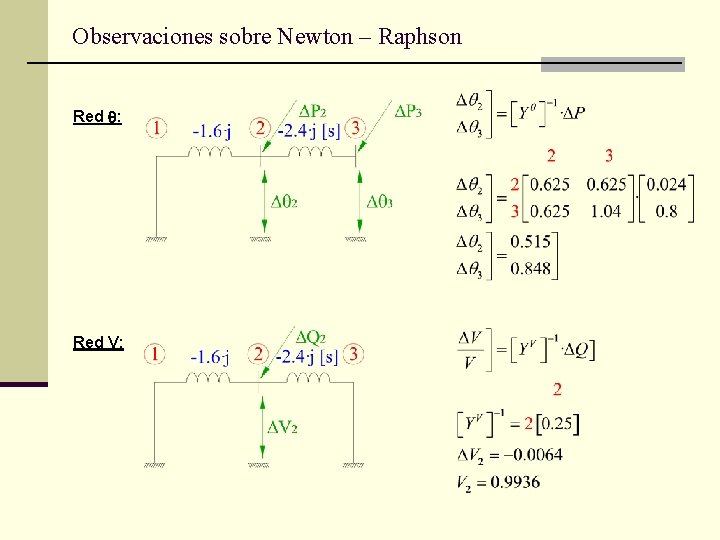
Observaciones sobre Newton – Raphson Red : ü ü ü Estructura similar a la red original. Barra libre conectada directamente a la referencia Las admitancias son Las corrientes inyectadas a los nodos son PS La magnitud de la tensión resultante son Red V: ü ü ü Estructura similar a la red original. Nodos con tensión especificada se conectan directamente a la referencia (Libre, PV) Las admitancias son Las corrientes inyectadas a los nodos son los Las tensiones resultantes son los V

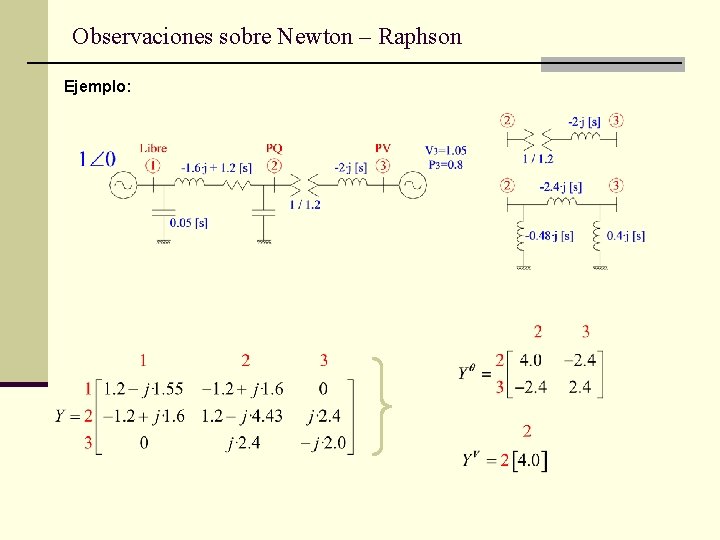
Observaciones sobre Newton – Raphson Ejemplo:

Observaciones sobre Newton – Raphson Red : Red V:

Observaciones sobre Newton – Raphson k=1 Red : Red V: k=2 Red : Red V: k=3 Red : Red V:

Observaciones sobre Newton – Raphson k=4 Red : Red V: k=6 Red : Red V:

Flujos de carga (minimización) Para resolver: Se construye: Pues cuando y es solución de En el problema de flujos de potencia, Obs 1: Si existe una solución, F se hará cero. Si F no se hace cero, el sistema está mal condicionado.

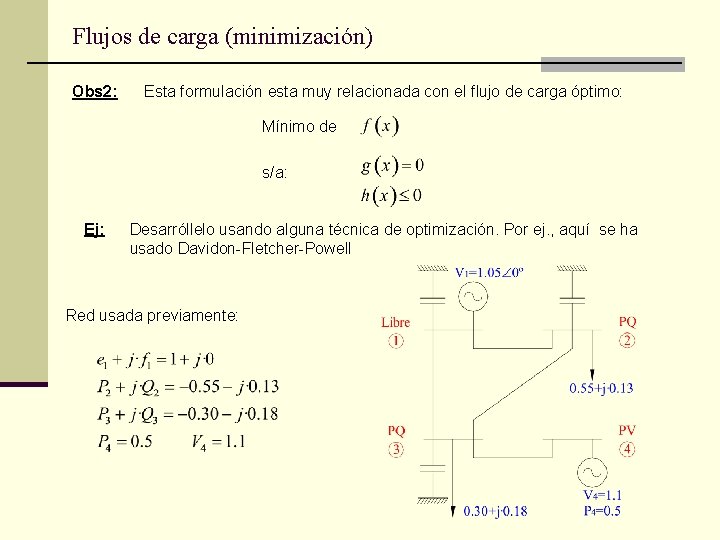
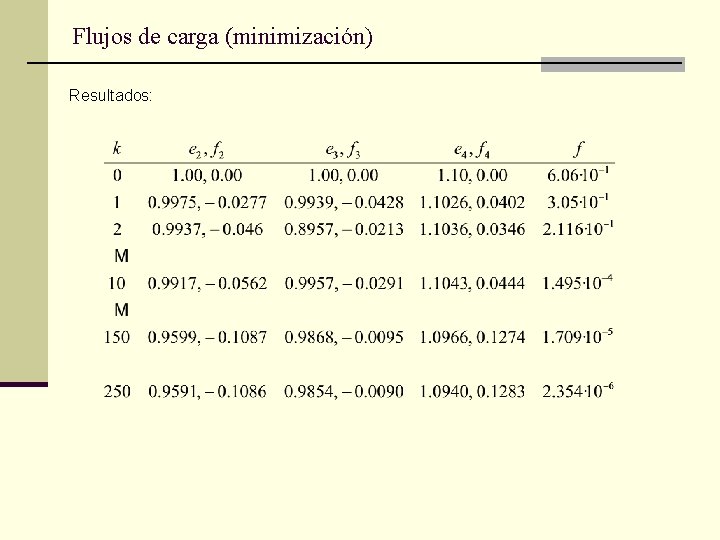
Flujos de carga (minimización) Obs 2: Esta formulación esta muy relacionada con el flujo de carga óptimo: Mínimo de s/a: Ej: Desarróllelo usando alguna técnica de optimización. Por ej. , aquí se ha usado Davidon-Fletcher-Powell Red usada previamente:

Flujos de carga (minimización) Resultados:

Flujos de potencias (Estructuras Con. Ed. )

Flujos de potencias (Controles) Control de tensión en generadores (PV) Se desea garantizar generadores en los límites permitidos de Q [MVAR] a) Si Q está dentro de los límites, se deja V en su valor. b) Si Q está fuera de rango, se varia V en la dirección apropiada Modo simple: PV PQLIM al témino de una iteración. Obs: - Debe vigilarse el valor de V resultante. - Debe corregirse el Jacobiano Control de tensión en una barra o control de flujo a través de un elemento. Modo simple: Si la cantidad controlada excede sus límites en alguna iteración, corregir la “derivación” en un salto en la dirección adecuada. Obs: - Lento, con múltiples posibilidades.

Flujos de potencias (Controles) Control de tensión en barra PQ Modo simple: Inyección de Q Control de intercambio (PI) Cargas con P, Q funciones de V

Flujos de potencias (Requerimientos) Tipo de solución: Exacto Sin Controles Fuera de Línea Cálculo Único Aproximado Controles En Línea Cálculos Múltiples

Flujos de potencias (Requerimientos) Propiedades requeridas de la solución Alta velocidad: Sistemas grandes. Aplicaciones en tiempo real. Casos repetitivos. Aplicaciones interactivas. Bajo almacenamiento: Sistemas grandes. Baja memoria disponible. Confiabilidad: Problemas mal condicionados. Estudios de colapso de sistemas. Estudios en tiempo real. Flexibilidad: Capacidad para manejar cambios y ajustes; para ser utilizados con otros procesos. Simplicidad: Codificación, mantención y mejoramiento.

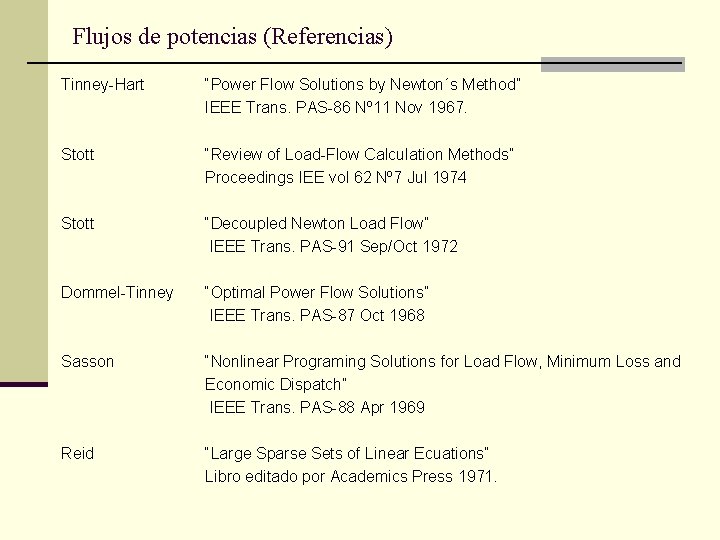
Flujos de potencias (Referencias) Tinney-Hart “Power Flow Solutions by Newton´s Method” IEEE Trans. PAS-86 Nº 11 Nov 1967. Stott “Review of Load-Flow Calculation Methods” Proceedings IEE vol 62 Nº 7 Jul 1974 Stott “Decoupled Newton Load Flow” IEEE Trans. PAS-91 Sep/Oct 1972 Dommel-Tinney “Optimal Power Flow Solutions” IEEE Trans. PAS-87 Oct 1968 Sasson “Nonlinear Programing Solutions for Load Flow, Minimum Loss and Economic Dispatch” IEEE Trans. PAS-88 Apr 1969 Reid “Large Sparse Sets of Linear Ecuations” Libro editado por Academics Press 1971.

Flujos de potencias (Referencias) Glimn-Satgg “Automatics Calculations of Load Flows” AIEE vol 76 Pt III pp 817 -828 1957 Tinney-Walker “Direct solutions of Network Ecuations by Optimally Ordered Triangular Factirization” Pica 1967 pp 367 -376 Stott-Alsac “Fast Decoupled Load Flow” IEEE Pas 93 May 1974

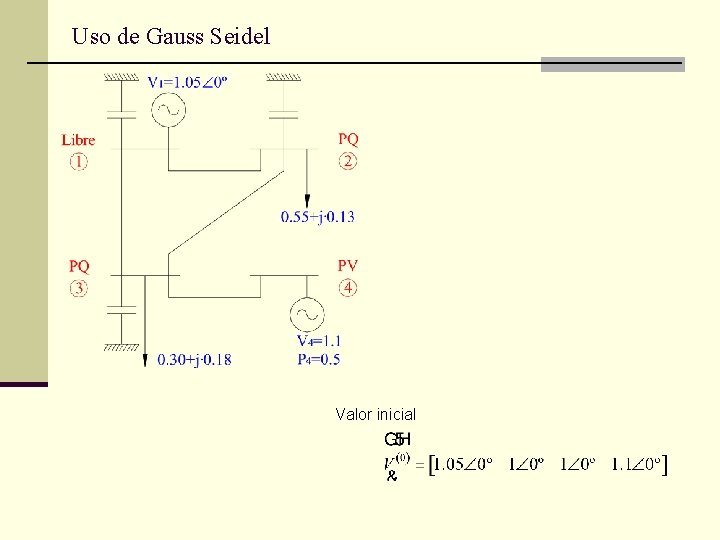
Uso de Gauss Seidel Valor inicial

Uso de Gauss Seidel k=1

Uso de Gauss Seidel k=1

Uso de Gauss usando Zbus Valor inicial k=1

Uso de Gauss usando Zbus

Uso de Newton Raphson El mismo ejemplo anterior: Coordenadas rectangulares: Valor inicial

Uso de Newton Raphson

Uso de Newton Raphson

Uso de Newton Raphson

Uso de Newton Raphson